求解黑箱全局优化问题的一种改进的随机算法

周 喆

(重庆师范大学 数学科学学院，重庆 401331)

求解黑箱全局优化问题的一种改进的随机算法

周 喆

(重庆师范大学 数学科学学院，重庆 401331)

提出了一个改进的随机算法求解黑箱全局优化问题，算法中使用的径向基函数插值是昂贵的目标函数的近似.算法在可靠的信赖域内通过简单而有效的方法选择下一个迭代点.在早期的迭代过程中,算法倾向于在响应面模型的全局最优值附近改善响应面模型的局部逼近精度.它可能暂时陷入局部最优,但它有能力在之后的迭代中探索可行域中的其他区域并改善响应面的全局逼近精度.数值实验结果说明了该算法的有效性.

全局优化; 昂贵的目标函数; 响应面模型; 径向基函数插值

本文主要考虑如下形式的全局优化问题：

minf(x)
s.t.a≤x≤b,x∈Rd

其中:f(x)∶Rd→R是一个昂贵的黑箱函数，也就是说它的函数估值代价非常大，a,b∈Rd.一般来说目标函数f(x)的导数信息是不可用的.令D=[a,b]表示上述问题的可行域.全局优化算法的任务是在可行域D中找到一个全局最优点x*使得对所有的x∈D都有f(x)≤f(x*).在实际中通过全局优化算法找到问题的精确的全局最优点是很困难的，所以一般只要求找到全局最优点x*的一个逼近点.

响应面方法作为一种流行的方法经常被用来求解此类优化问题.一般，响应面方法通过建立响应面模型来代替原有的模型来参与优化过程，响应面模型是真实的目标函数的比较廉价的近似.早期的响应面方法[1-2]通常采用低阶的多项式回归以及多变量插值并结合信赖域方法[3-4].后来，基于Kriging[5-6]、径向基函数(RBF)[7-9]的全局优化方法也逐渐被研究.此外，一些通过在一组随机生成的候点中选择下一个迭代点的随机响应面(SRS)方法[10-12]也被提出.对于求解黑箱全局优化问题，这些随机响应面(SRS)方法和其他流行的算法相比较显得更加有效.

本文基于径向基函数插值模型提出了一种改进的随机响应面方法，该方法的框架分为两个阶段：第一阶段，通过检测连续的两次响应面模型的全局最优值之间的欧式距离来确定是否选择当前的响应面模型的全局最优点作为下一个迭代点.如果没有执行这一步骤，则将下一个迭代点的探索区域限制在当前的响应面模型的全局最优点的附近，并在该区域内从一簇随机生成且服从正态分布的候选点中选择下一个迭代点；第二阶段，当连续多次迭代中得到的迭代点所对应的目标函数值没有产生实质性的改进的次数超过自定义的阈值时，则将探索区域扩充到整个可行域并在一簇均匀分布的随机候选点中选择下一个迭代点.另外，在这两个阶段中将采用一些基于极大极小距离的策略来保证选择的下一个迭代点不会太靠近已有的取样点.

1 预备知识

由于模型构造的简易性以及在全局逼近上的可靠性，径向基函数插值模型将被用来作为算法中的响应面模型.假设给定一个点集An={x1,x2,…,xn}⊂D以及相应的目标函数值f(x1),f(x2),…,f(xn).径向基函数插值模型被定义成如下形式[7]：

(1)

表1 径向基函数的常见形式

未知的参数λ,c能够通过求解如下线性方程组:

(2)

来得到，其中:

Φij=φ(‖x-xi‖),i,j=1,2,…,n,

F=(f(x1),f(x2),…,f(xn))T.

2 算法框架

接下来提出了一个基于响应面模型的改进的随机算法ISARS，该算法提供了非常有效的迭代搜索策略并能够保证局部搜索和全局搜索之间的平衡.在下面的符号中，n表示已有的取样点的数量，An={x1,x2,…,xn}表示已有的n个取样点的集合，离散的数据点集Bn={(x1,f(x1)),(x2,f(x2)),…,(xn,f(xn))}被用来构造响应面模型sn(x).

ISARS算法：

输入：

1)一个确定的定义在闭超矩形D=[a,b]⊂Rd上的目标函数f.

2)一个特别的响应面模型，比如带有尾部多项式的Cubic径向基函数插值模型.

3)一个采用对称拉丁超立方设计SLHD[15]生成的初始取样点集An0={x1,x2,…,xn0}⊂D.

6)允许进行的最多的函数估值次数Nmax.

7)每一次迭代中随机生成的试验点的数量k.(默认值：k=min(500 d,5 000).)

8)连续失败的迭代次数的阈值Tfail.(默认值：Tfail=min(5d+1,20).)

输出：算法停止迭代后计算出的最优解.

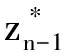
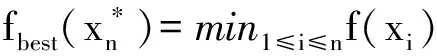
Step3.当不满足迭代终止条件(比如：当nlt;Nmax)时，执行

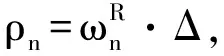
Step3.3 (选择下一个迭代点) 如果Cfaillt;Tfail，那么

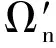
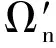
Step3.3(b)(i) (在整个可行域中随机生成试验点) 随机生成一组试验点集Ωn={yn,1,yn,2,…,yn,k}.对于j=1,2,…,k，yn,j=a+(b-a)⊗qj，其中qj∈Rd是一个随机生成的各分量在(0,1)上服从均匀分布的向量，⊗表示两个向量对应的分量相乘的运算.

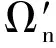
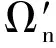
结束

Step3.4 (进行耗时的函数计算) 计算迭代点xn+1处的目标函数f(xn+1).

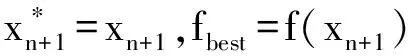
结束

3 算法分析

接下来分析算法中比较关键的一些步骤.在ISARS算法中，在拟合或者更新响应面模型(Step3.1)之前通常需要检测是否存在极端的目标函数值，因为极大或者极小的目标函数值会导致响面模型的波动剧烈而影响逼近精度.为了避免这一情况，当maxf(xi)-minf(xi)gt;2·103,xi∈An时，采用文献[9]中的对数转换函数对所有的目标函数值进行稳定化处理.φ(f)的函数表达式如下：

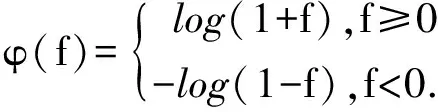
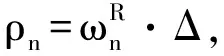
在Step3.3(a)(v)及Step3.3(b)(iii)中，从试验点集中选择下一个迭代点的过程采用文献[11]中的LMSRS方法和文献[12]中的DYCORS方法，但是ISARS算法预先对试验点进行了一次筛选排除了部分试验点(见Step3.3(a)(iv)以及Step3.3(b)(ii)).比如在二维平面上，以已有的取样点为中心的圆形之内的取样点都被排除掉.在进行全局搜索的情况下，当ρn比较小时，下一个迭代点更倾向于在已有的取样点附近来选择以提高局部逼近精度；而当ρn比较大时，选取的下一个迭代点更多地被限制在未完全探索的区域来提高全局逼近精度.

在主要的迭代过程中，ISARS算法通过阈值Tfail分为两个阶段.第一阶段，试验点在当前响应面模型的全局最优点附近随机生成并服从正态分布；第二阶段，试验点在整个可行域中随机生成并服从均匀分布.

此外，当算法陷入局部最优时，重启动策略作为一种有效地改进全局优化方法的策略很容易应用到ISARS算法中，在算法过程中仅需要设置一个重启动标志Rflag并初始化Rflag=0，当计数器Cfailgt;Tfail时，重启动标志重置为Rflag=1，这时ISARS算法将抛弃之前所有的数据信息重新开始执行算法的整个流程.

4 数值实验

本节将使用ISARS算法来求解维度在2到6之间的Dixon和Szegö[16]测试问题并将它与文献[11]中的LMSRS方法和文献[12]中的DYCORS方法的数值结果进行比较.这些问题的一些信息包括名称、维数、定义域、局部极小点的个数、全局最优点的个数以及全局最优值在表2中给出.其中，Branin测试问题的所有的局部极小点都是全局最优点，而对于其他的测试问题都只有一个全局最优点.

在进行比较的三种算法中，采用的响应面模型均是带有尾部多项式的Cubic径向基函数插值模型，并将采用了RBF插值模型的ISARS，LMSRS，DYCORS算法分别记作ISARBF，LMSRBF，DYCORBF算法.此外，结合了重启动策略的三种算法分别记为ISARBF-R，LMSRBF-R，DYCORBF-R算法.

表2 测试问题及其属性

对于同一个问题，每一种算法都运行30次.为了保证算法的公平性，对于求解同一个问题，不同的算法中初始取样点的位置保证是相同的.另外，LMSRBF算法和DYCORS算法中的参数都保持和原文献[11-12]中的一样.在ISARS算法中，设置RBF准则的权重模式为γ=〈0.02，0.25，0.5，0.95〉.

定义相对误差E为：

其中fglobal≠0是函数f的全局最优值.所有测试问题中，二维的问题允许进行的函数估值次数为200次，其他的问题允许进行的函数估值次数为500次.

表3中显示了各个算法对于求解同一问题在30次运行计算之后得到的最优解关于一些指标的统计结果.这些指标包括最优解中最好的值fglobal，最差的值fWorst，中值fMedian，平均值fmean，标准误差RMSE以及计算终止后找到的最优解与问题的最优解之间的相对误差为E≤1%下的成功率δSucc.

表3 算法运行30次之后得到的最优目标函数值关于各指标的统计结果

续表3

测试问题指标ISARBFISARBF-RLMSRBFLMSRBF-RDYCORSDYCORS-RShekel7fBest10．400010．401610．399010．399010．402710．3958fWorst5．116410．33621．83703．72201．83735．0880fMedian10．357710．38573．722510．38653．245010．3845fmean9．489110．37955．23859．59144．65629．6817RMSE1．95280．01693．20922．04652．98101．7908δSucc24/3030/308/3026/306/3026/30Shekel10fBest10．530810．531610．525210．532510．536310．5338fWorst5．164110．46601．67643．83322．421710．5035fMedian10．489310．51784．501410．52283．835410．5236fmean9．954210．51306．113710．11905．758210．5232RMSE1．59610．01913．69171．51143．48700．0075δSucc26/3030/3012/3028/3010/3030/30Hartman6fBest3．32213．32233．32233．32233．32243．3223fWorst3．10273．31963．17043．32163．20313．2015fMedian3．32003．32163．32233．32223．32233．3223fmean3．28883．32153．27943．32223．28663．3182RMSE0．06510．00060．06090．00010．05460．0217δSucc24/3030/3020/3030/3021/3029/30

分析表3中的数据可知，对于Branin测试问题，几种算法均找到了响应面模型的全局最优点，其中ISARBF-R算法以及DYCORS算法得到的最优值的平均值均为0.397 9并且标准误差均为0.000 1.对于Goldstein-Price测试问题，ISARBF-R算法的在所有的算法中得到的最优值平均值最低，并且在没有加入重启动策略的情况下，ISARBF算法在每一次运行中都找到了相对误差低于1%的全局最优值的逼近解.对于Hartman3测试问题，DYCORBF-R算法表现得最好.

对于Shekel类的测试问题，在没有加入重启动策略的情况下，ISARBF算法的表现要远优于LMSRBF算法和DYCORBF算法，因为其他两种算法在30次运行计算中找到相对误差低于1%的全局最优值的逼近解的运行次数比ISARBF算法少得多.另外，对于Shekel5和Shekel7测试问题，ISARBF-R算法在平均值，标准误差以及成功率这些指标上要优于其他的算法.对于Shekel10测试问题，DYCORBF-R算法找到的全局最优值更加精确并且在30次运行计算中都找到了相对误差低于1%的全局最优值的逼近解.对于Hartman6测试问题，虽然LMSRBF-R算法求得的最优解的标准误差是最低的，但是比较最差的最优解以及平均值可知，ISARBF-R算法的表现更好.

综合以上的分析可知，在没有加入重启动策略的情况下三种的算法中，ISARBF算法的表现要远远优于LMSRBF算法以及DYCORBF算法.虽然加入重启动策略后各个算法都相应的得到了改进，但是改进之后的算法在整体表现上来看还是ISARBF-R算法表现的更好.

[1]KHURIAI,CORNELLJA.Responsesurfaces[M].MDekker,1987.

[2]MYERSRH,MONTGOMERYDC.Responsesurfacemethodology:processandproductinoptimizationusingdesignedexperiments[J].Technometrics,1996,59(3):185-186.

[3]CONNAR,SCHEINBERGK,TOINTPL.Recentprogressinunconstrainednonlinearoptimizationwithoutderivatives[J].MathematicalProgramming,1997,79(1):397-414.

[4]POWELLMJD.Uobyqa:unconstrainedoptimizationbyquadraticapproximation[J].MathematicalProgramming,2002,92(3):555-582.

[5]HUANGD,ALLENTT,NOTZWI,etal.Globaloptimizationofstochasticblack-boxsystemsviasequentialkrigingmeta-models[J].JournalofGlobalOptimization,2006,34(3):441-466.

[6]JONESDR,SCHONLAUM,WELCHWJ.Efficientglobaloptimizationofexpensiveblack-boxfunctions[J].JournalofGlobalOptimization,1998,13(4):455-492.

[7]GUTMANNHM.Aradialbasisfunctionmethodforglobaloptimization[J].JournalofGlobalOptimization,2001,19(3):201-227.

[8] REGIS R G,SHOEMAKER C A.Constrained global optimization of expensive black box functions using radial basis functions[J].Journal of Global Optimization,2005,31(1):153-171.

[9] REGIS R G,SHOEMAKER C A.A quasi-multistart framework for global optimization of expensive functions using response surface models[J].Journal of Global Optimization,2013,56(4):1719-1753.

[10] REGIS R G.Stochastic radial basis function algorithms for large-scale optimization involving expensive black-box objective and constraint functions[J].Computers and Operations Research,2011,38(5):837-853.

[11] REGIS R G,SHOEMAKER C A.A stochastic radial basis function method for the global optimization of expensive functions[J].European Journal of Operational Research,2007,19(4):497-509.

[12] REGIS R G,SHOEMAKER C A.Combining radial basis function surrogates and dynamic coordinate search in high-dimensional expensive black-box optimization[J].Engineering Optimization,2013,45(5):1-27.

[13] BJRKMAN M,HOLMSTRM K.Global optimization of costly nonconvex functions using radial basis functions[J].Optimization and Engineering,2000,1(4):373-397.

[14] POWELL M J D.The theory of radial basis function approximation in 1990[C]//Light,W.(ed.),Advances in Numerical Analysis,Volume 2:Wavelets,Subdivision Algorithms and Radial Basis Functions,pp.105-210.Oxford University Press,1992.

[15] YE K Q,LI W,SUDJIANTO A.Algorithmic construction of optimal symmetric Latin hypercube designs[J].Journal of Statistical Planning and Inference,2000,90(1):145-159.

[16] DIXON L C W, G P.Towards global optimization 2[M].North-Holland Pub Co,1978.

责任编辑：时凌

AnImprovedStochasticAlgorithmforSolvingBlack-boxGlobalOptimizationProblems

ZHOU Zhe

(School of Mathematics Sciences，Chongqing Normal University，Chongqing 401331，China)

This paper proposes an improved stochastic algorithm for solving black-box global optimization by using radial basis function (RBF) interpolation which is an approximation of the expensive objective function.The algorithm selects the next iteration point by a simple and effective method in a reliable trust region.In the process of early iterations,algorithm tends to improve the local approximation accuracy around the global minimizer of response surface (RS) model.It may be temporarily trap in a local optimum,but it is capable of exploring other global region in latter iterations and improves the global approximation accuracy of response surface model.The numerical experiment results show the effectiveness of the algorithm.

global optimization;expensive objective functions;response surface model;radial basis function interpolation

2017-05-11.

重庆师范大学研究生科研创新项目(YKC16001).

周喆(1991-)，男，硕士，主要从事最优化计算方法的研究.

1008-8423(2017)04-0403-06

10.13501/j.cnki.42-1569/n.2017.12.011

O241.6

A