带有连续状态约束的最优控制问题的近似求解

包巴图吉力根,孙志玲

(内蒙古民族大学 数学学院，内蒙古 通辽 028000)

带有连续状态约束的最优控制问题的近似求解

包巴图吉力根,孙志玲

(内蒙古民族大学 数学学院，内蒙古 通辽 028000)

研究了带有连续状态不等式约束的最优控制问题.应用控制函数参数化方法将最优控制问题转换为有限维优化问题,应用积分熵函数将连续状态不等式约束近似为一般约束,证明了约束近似方法的收敛性.

最优控制;连续状态约束;非线性规划

最优控制是个重要的研究方向,它应用于很多方面,如工程、经济和金融等．最优控制问题的解一般没有解析表达式,因此最优控制的数值方法很重要．关于带有连续状态不等式约束的最优控制有很多研究[1-3]．文献[1-2]中给出一个光滑函数近似函数max{·,0},将连续状态约束近似为光滑的一般约束,结合控制参数化方法给出了计算方法．文献[3]中用离散化方法,将连续状态约束近似为有限多个一般约束,应用min max优化问题方法求解．熵函数方法是求解min max优化问题的一个有效方法[4-5]．

考虑带有连续状态不等式约束的最优控制问题．应用控制函数参数化方法将最优控制问题转换为有限维优化问题．应用积分形式的熵函数,将连续状态不等式约束近似为光滑的一般约束. 证明了约束近似方法的收敛性.

1 问题描述

考虑由下面常微分方程描述的系统:

(1)

其中:T为固定的终端时刻,x(t)∈Rn为状态变量,初始状态为x0∈Rn,u(t)∈Rr为控制函数,f∶Rn×Rr→Rn为给定的函数．

定义允许控制集:U={u∶[0，T]→Rr|u(t)}为分段连续函数,u(t)∈Ω,t∈[0，T]},其中Ω⊂Rr为有界闭凸集．

假设1 函数f连续可微,并且存在常数Kgt;0使得:

‖f(x(t),u(t))‖≤K(1+‖x‖),(x,u)∈Rn×Rr.

在满足假设1时,对u(·)∈U系统(1)存在唯一解,记为x(·|M).

下面给出最优控制问题:

(P1)minJ(u)=Φ(x(T|u))

s.t.u∈U,

h(x(t|u),u(t))≤0,∀t∈[0，T].

假设2 函数Φ和h连续可微.

2 问题近似

最优控制问题的解一般没有解析表达式,控制参数化是求解最优控制问题的一个有效数值方法．本文中取控制函数为分段常值函数.

令pgt;1为给定的整数,定义:

Γp={τ∈Rp+1|τ0=0,τp=T,Δ≥τi+1-τi≥δ,i=1,2,…,p-1}

其中:δgt;0为最小划分长度,Δgt;0为最大划分长度,且p→∞时Δ→0.τ∈Γp为区间[0，T]的一个划分．

定义1Ξp={σ∈Rp|σi∈Ω,i=1,2,…,p}.

(P2)minJp(u)=Φ(χp(T|σ,τ))

s.t. (σ,τ)∈Ξp×Γp,

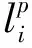
问题(P2)是个有限维优化问题,划分点τi是变动的,这样会使求解过程增加难度．应用时间转换方法[2]给出一个固定切换点的系统．

令θi=τi-τi-1,i=1,2,…,p.定义:Θp={θ∈Rp|θ1+θ2+…+θp=T,Δ≥θi≥δ,i=1,2,…,p}

令:

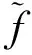
其中:Ii=[i-1,i),i=1,2,…,p-1和Ii=[i-1,i],i=p.由系统(1)得到新的系统:

(2)

y(i+)=y(i-),i=1,2,…,p-1

(3)

对(σ,θ)∈Ξp×Θp系统(2)～(3)存在唯一解,记为y(·|σ,θ).给出新问题(P3),

s.t. (σ,θ)∈Ξp×Θp,

h(y(s),σi)≤0,∀s∈Ii,i=1,2,…,p.

定理1 问题(P2)和问题(P3)等价．

证明过程可见文献[2]．

3 问题求解

问题(P3)中h(y(s),σi)≤0,∀s∈Ii是连续状态不等式约束,等价于下面的约束：

这里应用文献[5]中的方法,给出Hi(σ,θ)的光滑近似,

其中ρgt;1为逼近参数．

下面给出光滑近似的几个性质．

给出光滑近似问题(P4),

s.t. (σ,θ)∈Ξp×Θp,

由引理1和2可知对任何εgt;0存在充分大的ρ使得问题(P4)的最优解是问题(P3)的可行解．

假设3 问题(P3)的可行域Fp非空．

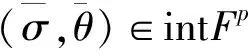
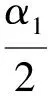
和

令ε→0,由δ1gt;0任意性,结论成立．

4 数值结果

考虑下面最优控制问题[6],求最优控制函数u∶[0，4.5]→R,目标为：

系统方程为:

初始状态为:

x1(0)=-5,x2(0)=-5,

约束为:

[1] TEO K L,JENNINGS L S.Nonlinear optimal control problems with continuous state inequality constraints [J].Journal of Optimization Theory and Applications,1989,63(1):1-22.

[2] LOXTON R C,TEO K L,REHBOCKA V,et al.Optimal control problems with a continuous inequality constraint on the state and the control [J],Automatica,2009 45:2250-2257.

[3] POLAK E,YANG T H,MAYNE D Q.A method of centers based on barrier functions for solving optimal control problems with continuous state and control constraints [J].SIAM Journal on Control and Optimization,1993,31: 159-179.

[4] PEE E Y,ROYSET J O.On solving large-scale finite minimax problems using exponential smoothing [J].Journal of Optimization Theory and Applications,2011,148: 390-421.

[5] 周广路,王长钰,张玉忠.半无限规划问题的一个有效解法 [J].计算数学,1999,21(1) :3-8.

[6] GERDTS M.Global convergence of a nonsmooth Newton method for controlstate constrained optimal control problems [J].SIAM Journal of Optimization,2008,19(1):326-350.

[7] JENNINGS L S,TEO K L,FISHER M E,et al.Miser 3.2 optimal control software:Theory and User Manual[M].Australia:Department of Mathematics and statistics,The University of Western Australia.1997.

责任编辑：时凌

ApproximationMethodforOptimalControlProblemswithaContinuousInequalityConstraint

BAO Batujiligen,SUN Zhiling

(College of Mathematics,Inner Mongolia University for nationalities,Tongliao 028000,China)

We consider optimal control problems with a continuous inequality constraint.By using control parametrization method，optimal control problem can be transformed into a finite dimensional optimization problem.Continuous inequality constraint is approximated by a smooth function.The convergence result of constraint approximation is given.

optimal control;continuous state inequality constraint; nonlinear programming

2017-05-25.

内蒙古自治区自然科学基金项目(2014BS0106); 内蒙古民族大学博士科研启动基金项目(BS376) .

包巴图吉力根(1982-),男(蒙古族),博士,讲师,主要从事运筹学与控制论的研究.

1008-8423(2017)04-0387-03

10.13501/j.cnki.42-1569/n.2017.12.007

O232

A