不同水深水下爆炸载荷作用下多孔覆盖层有效厚度工程估算方法
殷彩玉, 金泽宇, 谌 勇, 华宏星
(上海交通大学 机械系统与振动国家重点实验室,上海 200240)
不同水深水下爆炸载荷作用下多孔覆盖层有效厚度工程估算方法
殷彩玉, 金泽宇, 谌 勇, 华宏星
(上海交通大学 机械系统与振动国家重点实验室,上海 200240)
针对芯层为塑性多孔材料的抗冲覆盖层在深水非接触爆炸载荷作用下的有效厚度开展了理论研究。建立了完整的考虑覆盖层大变形、流固耦合效应、空化效应及静水压力作用的理论模型,用以求解覆盖层的有效厚度。分析了冲击环境变化及覆盖层参数变化对有效厚度的影响,得到了覆盖层有效厚度估算公式。研究结果为多孔覆盖层用于深水爆炸冲击防护的设计提供了工程估算方法。
水下爆炸;多孔覆盖层;有效厚度;工程估算方法
塑性多孔泡沫具有低密度、比力学性能高的特点,被广泛应用于冲击防护[1-3]。当其被用于水下舰船的冲击防护时,一方面可以降低传递到舰船壳体的冲量,另一方面可以吸收冲击波能量,降低壳体的响应。与超弹性的橡胶覆盖层[4-5]相比,多孔塑性泡沫可以耐静压,有更宽的应力平台,从而吸收更多的冲击波能量。
多孔材料的宏观力学特性具有典型的三阶段特性:弹性阶段、应力平台阶段及密实化阶段。在线弹性阶段,应变一般小于5%;在应力平台阶段,可发生大的塑性变形并吸收大量冲击波能量,同时传递到壳体的应力较低;在密实化阶段,传递到壳体的应力急剧上升,而多孔材料的吸能量很少。已有不少研究证明,当覆盖层发生密实化后会降低其冲击防护效果。Cooper等[6]研究了多孔材料对动物的防护效果,结果表明冲击波经过多孔材料再传递到动物身上时,对动物的内脏产生更大的伤害。Ben-Dor等[7]在开展多孔材料应力传播的实验时也发现了类似的现象。Li等[8]建立了一维质量-弹簧系统来分析这一现象。后来,Harrigan等[9]的研究表明只有当多孔材料被完全压溃后才会出现应力硬化的现象。因此,在设计中要避免让多孔材料发生密实化。最近,Turkyilmazoglu[10]研究了泡沫在空爆时发生密实化的条件。对于水下爆炸,由于流固耦合及空化的发生,使问题变的更为复杂。因此,要得到多孔覆盖层有效厚度的显式表达就变的很困难。这里,覆盖层的有效厚度指冲击波能量刚好被完全耗散时压溃的覆盖层的厚度。而到目前为止,也没看到相关方面的研究工作。
本文主要研究多孔覆盖层在不同水深水下爆炸时有效厚度的工程估算方法。首先建立考虑覆盖层大变形、流固耦合、空化及静水压力的理论模型,计算覆盖层的有效厚度。然后运用有限元分析验证理论模型的有效性。并利用已验证的理论模型分析冲击环境参数变化及覆盖层参数变化对多孔材料有效厚度的影响。最后通过参数分析的结果,总结出覆盖层有效厚度的工程估算方法,得到覆盖层有效厚度的显式表达式。
1 理论模型
多孔覆盖层由面板(面密度mf)和塑性泡沫芯层组成;舰艇壳体假设固定,静水压力为pst。坐标原点取在流固耦合面上,如图1(a)所示。沿正向传播的入射冲击波作用在覆盖层上,入射冲击波可表示为指数衰减波的形式[11]
pm=p0e-t/θ
(1)
式中:p0为冲击波峰值;θ为衰减系数。

(a)

(b)图1 多孔覆盖层受水下爆炸冲击波和空化溃灭过程Fig.1 Sketch of cellular cladding to water blast and cavitation closure
多孔泡沫芯层的材料模型用刚塑性模型来描述,其密度、屈服强度和密实化应变分别为ρ0、σ0、εD。在冲击波作用下,覆盖层被快速压缩,根据塑性冲击波理论[12],冲击波波后的动态应力可表示为
σD=σ0+ρ0V2/εD
(2)
式中,V为被压溃覆盖层的速度。覆盖层前面板及被压溃部分以速度V一起运动。根据牛顿第二定律,覆盖层的运动方程为
(3)
式中:u为面板的位移,满足du/dt=V;pwet为湿表面的压力。根据Taylor板理论[13],流固耦合面上的总压力可以表示为静水压力pst、入射压力pin、反射压力pr及由于覆盖层运动产生的稀疏波的总和
pwet=pst+pin+pr-ρwcwV
(4)
式中,ρw、cw分别为水的密度和声速。
覆盖层被快速压溃过程中产生的稀疏波会使水发生空化。水中位置x处的压力和速度可表示为
pw(t,x)=pst+pin+pr-ρwcwdu/dt
(5)

(6)
空化发生时有pw(t,x) = 0,代入式(6),得到位于x处水粒子的空化速度为
(7)
式中,tcav为x处水粒子发生空化的时刻。
空化的传播及溃灭与文献[14-16]类似,这里不再赘述。向湿表面传播的空化最终会发生溃灭,产生二次加载波(重构波)pCF,out,作用在覆盖层上,如图1(b)所示。假设重构波的波阵面此时位于xCF处,由于空化溃灭所辐射的波可以表示

(8)
(9)
空化的发生,截断了水中的入射压力,同时,由于空化溃灭又重新辐射压力作用到覆盖层上。记作用到覆盖层上的真实入射压力为pa,其可表示为
(10)
式中,t0为空化溃灭辐射的二次加载波首次传播到湿表面的时间。假设覆盖层面板的刚度要远大于水的刚度,则流固耦合面总压力为
pwet=pst+2pa-ρwcwV
(11)
联立式(3)、式(8)~式(11),并考虑初始条件
u=0, du/dt=V=0
(12)
可准确求得塑性多孔覆盖层的有效厚度u/εD。
2 数值验证
为了验证理论模型的正确性,用商业有限元软件ABAQUS/Explicit对所分析的对象进行建模计算。覆盖层面板取1 mm厚的钢板,其密度、弹性模型和泊松比分别为7 800 kg/m3、2.1×1011Pa和0.3。水的长度为3 m,密度和声速分别为1 000 kg/m3和1 500 m/s。覆盖层芯层的材料选用密度为150 kg/m3的刚性聚氨酯泡沫,其屈服强度和密实化应变分别为1.465 9 MPa和0.566 7。入射指数衰减波的峰值为30 MPa,衰减系数为0.045 92 ms。分别考虑静水压力为0 MPa和1 MPa两种工况。
在有限元模型中,覆盖层采用平面应变单元模拟,水采用声学单元模拟。水发生空化的条件为压力降为0。沿冲击波传播方向,单元的尺寸为0.012 5 mm。
图2给出了理论方法和有限元计算得到的湿表面压力结果。湿表面压力峰值接近60 MPa,为了使压力曲线中的应力平台能更好的显示出来,压力曲线的峰值被截断了。从图2可知,两种方法计算的结果吻合很好。与给定的入射冲击波pin相比,湿表面压力在流固耦合作用下快速下降,随后出现一个应力平台,其值与覆盖层多孔材料的屈服强度相当。随着静水压力增加,湿表面压力曲线的形状变化不大,但是应力平台持续的时间会变长。

图2 理论及有限元计算得到的湿表面压力结果Fig.2 The pressure at the wetted interface by the two methods
图3给出了两种方法计算得到的覆盖层的压缩速度和传递到结构的应力。可以看出,多孔材料在压缩过程中,传递到结构的应力始终等于多孔材料的屈服强度,与冲击波的大小无关,前提是覆盖层没有完全密实化。理论结果与有限元结果吻合很好,证明了理论模型的有效性。
对有限元模型进行反复试算,得到冲击波能量刚好耗散完时覆盖层的有效厚度,并与理论结果进行对比,如表1所示,两者结果吻合很好。

表1 理论及有限元计算得到的覆盖层有效厚度

图3 覆盖层面板的运动速度及传递到舰船壳体的应力Fig.3 The velocity of the cellular cladding and the stress transmitted to the protected structure
3 参数分析
在第“1”节中我们给出了计算覆盖层有效厚度的理论模型,通过数值求解式(3)、式(8)~式(11),即可得到覆盖层在给定冲击载荷作用下的有效厚度。在第“2”节中通过数值验证,证明了理论模型的有效性。显然地,覆盖层的有效厚度与冲击环境和覆盖层参数有关。本节运用已验证过的理论模型分析参数变化对有效厚度的影响,为有效厚度的工程估算做准备。定义无量纲的参量为


(13)
式中:ψ为流固耦合参数;I0=2p0θ为最大冲量。
无量纲后,运动方程可表示为
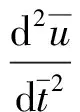
(14)
其中,
(15)
(16)
(17)
经无量纲化后,剩下p0一个参数,下面的分析中,我们选参考的入射压力峰值为pref=30 MPa来进行分析。覆盖层的有效厚度为u/εD与压缩量u密切相关,因此,下面用压缩量u来评估覆盖层的有效厚度。
3.1 流固耦合参数的影响
图4给出了流固耦合参数变化对覆盖层压缩量的影响。从图4可知,只有当流固耦合参数较小时,可以减小覆盖层的压缩量。根据流固耦合参数的定义,ψ=ρwcwθ/mf,可知,ψ减小意味着增加覆盖层面板的质量。对于实际的覆盖层来讲,面板是很薄的一层,质量不可能太大。因此,流固耦合参数的影响可忽略。

图4 流固耦合参数ψ变化对覆盖层压缩量的影响(pref = 30 MPa, ρ0/ρw = 0.2, εD = 0.7, pst = 0)Fig.4 The effects of the FSI parameter, ψ, on the non-dimensional stroke
3.2 多孔材料参数的影响
多孔材料的参数包括密度、屈服强度和密实化应变三个参量。覆盖层的压缩量与密实化应变无关,因此这里只考虑多孔材料的密度和屈服强度的影响,如图5和图6所示。对比图5和图6可知,多孔材料的密度对覆盖层的压缩量影响很小,可忽略;而屈服强度对覆盖层的压缩量影响很大,屈服强度越高,压缩量越小。这是因为,屈服强度越高,覆盖层单位体积的吸能量越多,因此吸收冲击波能量所需的覆盖层厚度越薄。我们发现,覆盖层的压缩量可拟合得到如下表达式
(18)
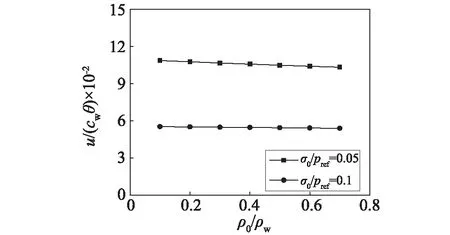
图5 多孔材料密度变化对覆盖层压缩量的影响(pref=30 MPa, ψ=20, εD=0.7, pst = 0)Fig.5 The effects of the foam density on the non-dimensional stroke
3.3 冲击波峰值的影响
冲击波峰值变化对于覆盖层压缩量的影响,如图7所示。从图7可知,保持σ0/p0不变,增加p0,覆盖层压缩量线性增加。对于曲线上的任意两点A1和A2,满足

(19)
注意:式(19)满足的前提是σ01/p01=σ02/p02。
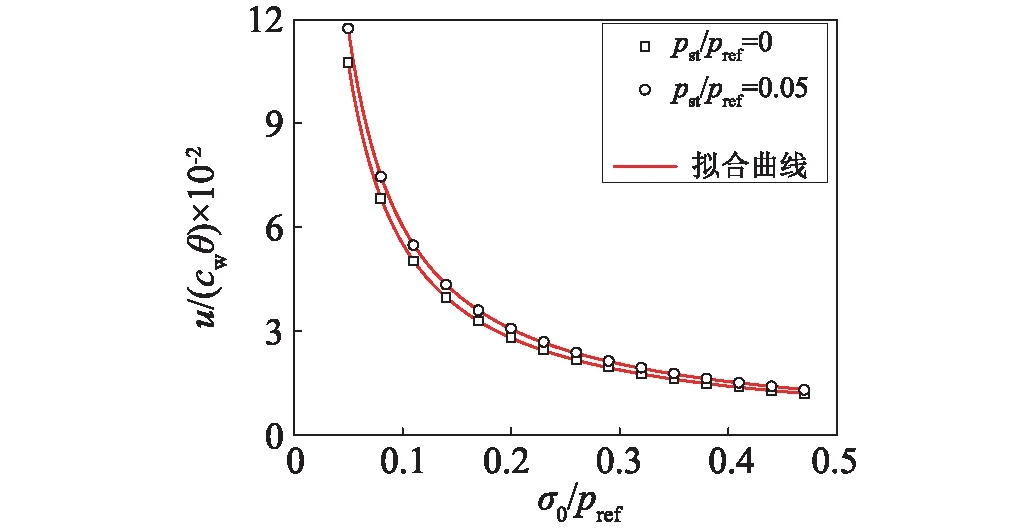
图6 多孔材料屈服强度变化对覆盖层压缩量的影响(pref=30 MPa, ψ= 20, ρ0/ρw = 0.2, εD = 0.7)Fig.6 The effects of foam strength on the non-dimensional stroke

图7 入射冲击波峰值变化对覆盖层压缩量的影响(ψ= 20, ρ0/ρw=0.2, εD = 0.7, pst = 0)Fig.7 The effects of the incident peak pressure on the non-dimensional stroke
3.4 静水压力的影响
通过计算发现,随着静水压力增加,覆盖层的压缩量也增加。对于某一多孔材料及给定的入射冲击波,定义其考虑静水压及不考虑静水压时的有效厚度增加率(或压缩量增加率)为
δ=(Leff|pst-Leff|pst=0)/Leff|pst=0
(20)
式中:Leff|pst=0和Leff|pst分别为静水压力为0时的有效厚度和静水压力为pst时的有效厚度。通过大量计算发现,δ只与无量纲的静水压力值有关,如图8所示。图8中的结果,可用多项式拟合方式,得到
δ=1.758 6(pst/p0)+1.688 42(pst/p0)2
(21)
4 覆盖层有效厚度工程估算方法
4.1 覆盖层有效厚度估算公式
通过第“3”节的参量分析结果可知:流固耦合参数、覆盖层密度的影响可忽略;冲击波峰值、覆盖层屈服强度以及静水压力的影响较大。根据第“3”节的结果,我们可以总结出通过式(18)~式(20)求解任意屈服强度的覆盖层在任意冲击波载荷下的有效厚度。对于任意给定的冲击环境(p0,θ,pst),覆盖层参数(ρ0,σ0,εD),覆盖层有效厚度Leff的求解步骤如下:
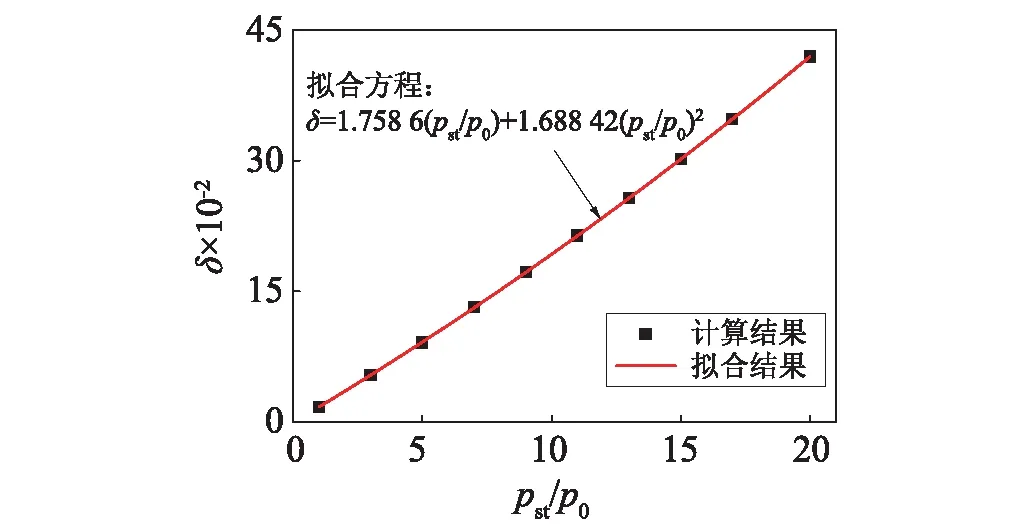
图8 静水压力变化对覆盖层有效厚度变化率的影响(ψ= 20, ρ0/ρw = 0.2)Fig.8 The increment rate of the effective foam thickness as a function of the normalized static pressure
步骤1 根据式(18),求解等效强度为σref的覆盖层在参考压力峰值pref及静水压力为0时的压缩量

(22)
式中,σref/pref=σ0/p0。
步骤2 根据式(19),求解强度为σ0的给定覆盖层在给定压力峰值p0及静水压力为0时的压缩量
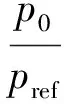
(23)
步骤3 根据式(20),求解强度为σ0的给定覆盖层在给定压力峰值p0及静水压力为pst时的压缩量
u3=(1+δ)u2=
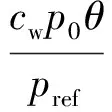
(24)
步骤4 计算覆盖层的等效厚度

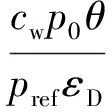
(25)
式中:pref= 30 MPa;cw=1 500 m/s为水中冲击波的传播速度。
式(25)中包含冲击环境参数(p0,θ,pst)和覆盖层特性参数(σ0,εD),给出了任意覆盖层在任意冲击环境下的有效厚度估算公式。
注意:静水压力与覆盖层屈服强度满足pstlt;σ0,这是因为若覆盖层在静水压力作用下已压溃,则其已经不具有抗冲击的特性,再研究其冲击防护效果已无意义。
4.2 覆盖层有效厚度工程估算公式的应用算例
在第“4.1”节中,我们推导出多孔泡沫覆盖层有效厚度的工程估算公式,即式(25)。现在我们给出一个应用算例。现有两种不同密度的刚性聚氨酯泡沫,通过压缩实验,得到其名义应力-应变曲线,如图9所示。其等效刚塑性模型的参数如表2所示。

图9 两种刚性聚氨酯泡沫压缩时的名义应力-应变曲线Fig.9 The nominal stress-strain curve of polyurethane foam

表2 两种不同刚性聚氨酯泡沫等效刚塑性模型参数
冲击环境通常采用冲击因子来描述,壳体冲击因子的定义为
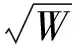
(26)
式中:W为炸药的质量;R为爆源到目标的直线距离。对于同一冲击因子,不考虑静水压力时,同一冲击因子的不同的(p0,θ)组合对舰船的破坏程度相当,即峰值高、脉宽短的冲击波的破坏程度和峰值低、脉宽长的冲击波的破坏程度相当。因此,本节计算同一冲击因子不同(p0,θ)组合时覆盖层的有效厚度,若计算得到的有效厚度差不多,亦可反映覆盖层有效厚度估算公式的可行性。
水下爆炸冲击波的峰值和衰减系数可表示为
(27)
(28)
对于TNT炸药,如果取国际单位制,则K1=53.4,A1= 1.13,K2=0.092 5,A2=-0.22。图10给出了不同壳体冲击因子时所对应的冲击波的不同(p0,θ)组合。

图10 不同壳体冲击因子与冲击波峰值及衰减系数的关系Fig.10 The shock wave for shock factor with different values
应用式(25),我们计算了两种聚氨酯泡沫在不同冲击因子及静水压力时的有效厚度,分别如图11和图12所示。对比结果可知:
(1) 对于同样的冲击因子,屈服强度高的PUR2泡沫的等效厚度更薄,这是因为PUR2单位体积的吸能量比PUR1泡沫高;
(2) 当静水压力为0时,同一冲击因子不同(p0,θ)组合时,计算得到的等效厚度基本相同,这也反映了同一冲击因子下的冲击波破坏强度相当,与冲击因子的定义吻合;
(3) 当考虑静水压力时,同一冲击因子的等效厚度不再相同,对于冲击波峰值小、衰减系数大的组合,等效厚度更厚。这是因为此时静水压力与冲击波峰值的比值更大,静水压力的影响更大,如“3.4”节的结果所示。

图11 PUR1泡沫在不同冲击因子及静水压力时的有效厚度Fig.11 The effective thickness of PUR1 foam under different shock factor and static pressure

图12 PUR2泡沫在不同冲击因子及静水压力时的有效厚度Fig.12 The effective thickness of PUR2 foam under different shock factor and static pressure
4 结 论
本文对多孔抗冲覆盖层在不同水深水下爆炸冲击载荷下的有效厚度开展了理论分析。根据所分析问题的特点,建立了完整的考虑覆盖层大变形、流固耦合效应、空化效应及静水压力影响的理论模型,用以计算覆盖层的有效厚度。采用商业有限元软件ABAQUS/Explicit验证了理论模型的有效性。利用已验证的理论模型分析了冲击环境变化及覆盖层参数变化对有效厚度的影响。得到了塑性多孔覆盖层关于冲击环境参数和多孔材料参数的有效厚度估算公式。研究结果可以为多孔覆盖层用于不同深度水下爆炸冲击防护的设计提供参考。
本文的研究结果是基于一维的理论结果,考虑的是平面冲击波。对于实际的水下爆炸,冲击波是球面波,作用于结构不同位置处的冲击波也不同。因此,在以后的工作中,我们期望能推导出适用于二维甚至三维问题的结果,为实际工程应用提供更准确的参考。
[ 1 ] FLECK N A, DESHPANDE V S. The resistance of clamped sandwich beams to shock loading [J]. Journal Applied Mechanics, 2004,71(3):386-401.
[ 2 ] TILBROOK M T, DESHPANDE V S, FLECK N A. The impulsive response of sandwich beams: analytical and numerical investigation of regimes of behavior [J]. Journal of the Mechanics and Physics of Solids, 2006,54(11):2242-
2280.
[ 3 ] MCSHANE G J, DESHPANDE V S, FLECK N A. Underwater blast response of free-standing sandwich plates with metallic lattice cores [J]. International Journal of Impact Engineering, 2010,37(11):1138-1149.
[ 4 ] 谌勇,华宏星,汪玉,等.超弹性夹芯覆盖层的水下爆炸防护性能[J].爆炸与冲击,2009,29(4):395-400.
CHEN Yong, HUA Hongxing, WANG Yu, et al. Protective effects of hyper-elastic sandwiches coated onto metal boxes subjected to underwater explosion [J]. Explosion and Shock Waves, 2009, 29(4): 395-400.
[ 5 ] 章振华,谌勇,华宏星,等.超弹性夹芯覆盖层抗冲击性能分析及实验研究[J].振动与冲击,2012,31(5):132-134.
ZHANG Zhenhua, CHEN Yong, HUA Hongxing, et al. Simulation and test for hyperelastic sandwich coatings in crush dynamics [J]. Journal of Vibration and Shock, 2012, 31(5):132-134.
[ 6 ] COOPER G J, TOWNEND D J, CATER S R, et al. The role of stress waves in thoracic visceral injury from blast loading: Modification of stress transmission by foams and high-density materials [J]. Journal of Biomechanics, 1991, 24(5): 273-285.
[ 7 ] BEN-DOR G, MAZOR G, IGRA O, et al. Shock wave interaction with cellular materials. Part II: open cell foams; experimental and numerical results [J]. Shock Waves, 1994, 3(3): 167-179.
[ 8 ] LI Q M, MENG H. Attenuation or enhancement-a one-dimensional analysis on shock transmission in the solid phase of cellular material [J]. International Journal of Impact Engineering, 2002, 27(10): 1049-1065.
[ 9 ] HARRIGAN J J, REID S T, YAGHOUBI A S. The correct analysis of shocks in a cellular material[J]. International Journal of Impact Engineering, 2010, 37(8): 918-927.
[10] TURKYILMAZOGLU M. Air blast response of compaction foam having a deformable front face panel incorporating fluid structure interactions[J]. International Journal of Mechanical Science, 2016, 105: 340-347.
[11] COLE R H. Underwater explosions[M]. Princeton: Princeton University Press, 1948.
[12] DAVISON L. Fundamentals of shock wave propagation in solids [M]. Berlin: Springer, 2008.
[13] TAYLOR G I. The pressure and impulse of submarine explosion waves on plates [C]∥ In the Scientific Papers of G.I. Taylor, vol. III. Cambridge: Cambridge University Press,1963: 287-303.
[14] KENNARD E H. Cavitation in an elastic liquid [J]. Physical Review, 1943,63(5/6): 172-181.
[15] SCHIFFER A, TAGARIELLI V L, PETRINIC N, et al. The response of rigid plates to deep water blast: analytical models and finite element predictions [J]. Journal of Applied Mechanics, 2012,79(6): 061014.
[16] YIN C, JIN Z, CHEN Y, et al. One-dimensional response of single/double-layer cellular cladding to water blast [J]. International Journal of Impact Engineering, 2016, 88: 125-138.
Anengineeringmethodforestimatingtheeffectivethicknessofcellularcladdingstowaterblast
YIN Caiyu, JIN Zeyu, CHEN Yong, HUA Hongxing
(The State Key Laboratory of Mechanical System and Vibration, Shanghai Jiao Tong University, Shanghai 200240, China)
This paper was devoted to derive an explicit expression of the effective foam thickness subjected to deep underwater explosion. One-dimensional analytical model considering the large deformation of cladding, fluid-structure interaction, the cavitation phenomenon and the initially applied hydrostatic pressure was built up to calculate the effective foam thickness. The results provide an engineering estimating method for the design of such cellular claddings under deep water blast.
underwater explosion; cellular cladding; effective foam thickness; engineering estimating method
国家自然科学基金(11272215)
2016-05-06 修改稿收到日期: 2016-07-27
殷彩玉 女,博士,1988年生
谌勇 男,博士,副研究员,1977年生
O383+.1
A
10.13465/j.cnki.jvs.2017.22.010

