基于小波包和拉普拉斯特征值映射的柱塞泵健康评估方法

王浩任， 黄亦翔， 赵 帅， 刘成良， 王双园， 张大庆

(1.上海交通大学 机械系统与振动国家重点实验室，上海 200240; 2.山河智能装备集团，长沙 410100)

基于小波包和拉普拉斯特征值映射的柱塞泵健康评估方法

王浩任1， 黄亦翔1， 赵 帅1， 刘成良1， 王双园1， 张大庆2

(1.上海交通大学 机械系统与振动国家重点实验室，上海 200240; 2.山河智能装备集团，长沙 410100)

柱塞泵是液压系统的关键部件之一，监测其健康状态对液压系统的可靠运行具有重要意义。提出一种基于小波包和流形学习的方法，用于分析柱塞泵出口振动信号，从而对其进行健康评估；该方法利用小波包对原始信号进行分解，从中提取用于描述柱塞泵健康状态的有效特征群；把提取的高维特征群作为输入，利用并比较多种流形学习方法进行特征降维，选取状态识别准确率最高的拉普拉斯特征映射方法，建立起的特征向量到健康状态之间的对应关系，实现液压泵健康状态监测的分类要求。实验结果表明，采用小波包和拉普拉斯特征映射相结合的方法可以有效提高柱塞泵状态评估的准确性。

小波包分析；流形学习；柱塞泵；拉普拉斯特征映射；健康状态评估

液压泵广泛应用于各种工业场合，但液压泵健康评估机理复杂，缺乏理论研究模型，且检测信号所包含的噪声较多，所以难以对健康状态识别。当液压泵处于故障初期，一般表现为振动、冲击、噪声增加，并制约生产效率提高；随着故障不断加剧，液压泵往往会因为故障引起压力下降，最终导致液压泵不能正常工作，甚至造成严重的安全事故。因此，通过对液压泵的健康状态的评估，判断液压泵的运行状态，从而对可能产生的故障进行预防，具有极其重要的作用。小波分解(Wavelet Decomposition, WD)[1-2]是一种时频域分解的方法，适用于非平稳信号的分解。小波包分解(Wavelet Package Decomposition, WPD)[3]利用一对高通滤波器和低通滤波器，能对信号的高频和低频成分作同样的精细的分解。运用小波包的分析方法，弥补了小波分解对高频信号分辨率的不足。对于具有非平稳特性的实际柱塞泵振动信号，需要对高频和低频信号成分进行较为全面的分析。使用小波包分解，能够更好地提取信号的特征，获得信号的潜在信息。

流形学习是一种用于高维空间数据降维的算法，作为一种维数约简的手段，能挖掘高维非线性数据的几何特征，从而在复杂的非线性空间中获取信息。自Science杂志首次发表与流形学习相关算法后，相继出现了局部线性嵌入算法(Local Linear Embedding, LLE)[4]、等距特征映射(Isometric Mapping, ISOMAP)[5]、拉普拉斯特征值映射(Laplacian Eigenmaps, LE)[6]、局部保持投影映射算法(Locality Preserving Projections, LPP)[7-8]等。其中流形学习在一些常见机械设备的故障诊断中已有应用：Jiang等[9]提出了监督拉普拉斯映射算法，并成功应用到了齿轮箱的故障诊断中；Yu等[10]提出了LPP的改进算法，并运用在轴承的故障检测和状态评估中；王红军等[11]提出了局部切空间排列算法(Local Tangent Space Alignment，LTSA)在数控机床上的应用，并成功用于机床主轴的状态评估。虽然流形学习方法在一些常见的机械设备已经有了一定的研究，但对柱塞泵等液压元件尚未应用。

针对目前国内外研究现状，本文提出了一种针对柱塞泵健康评估研究方法。采用小波包分解对信号预处理，并提取时域特征作为高维特征向量。通过拉普拉斯特征映射等流形学习方法对高维特征向量进行降维处理，并使用K最近邻方法(K-Nearest Neighbors, KNN)验证分类效果。实验结果表明，所提出的健康评估的方法能够提高辨识精度，对柱塞泵的健康状态识别具有重要的作用。

1 小波包系数分解

本文利用小波包对非平稳随机的柱塞泵振动信号进行分解，能够获得信号在某一时间点的频率特性。同时，小波包能够更加精细地对原始信号进行分解和重构，细化不同健康状态对应的信号频率范围，有利于准确评估健康状态，提高模型对柱塞泵可靠性。小波包通过分解应用一对相关联的低通滤波器和高通滤波器，将信号序列分解为某一尺度下的低频和高频两部分。在改变尺度对已分解的低频部分和高频部分再次进一步分解，获取更为细化的频率成分。这种分解可以进行多次，以达到所需要的频率分辨率。图1为小波包三层分解示意图。

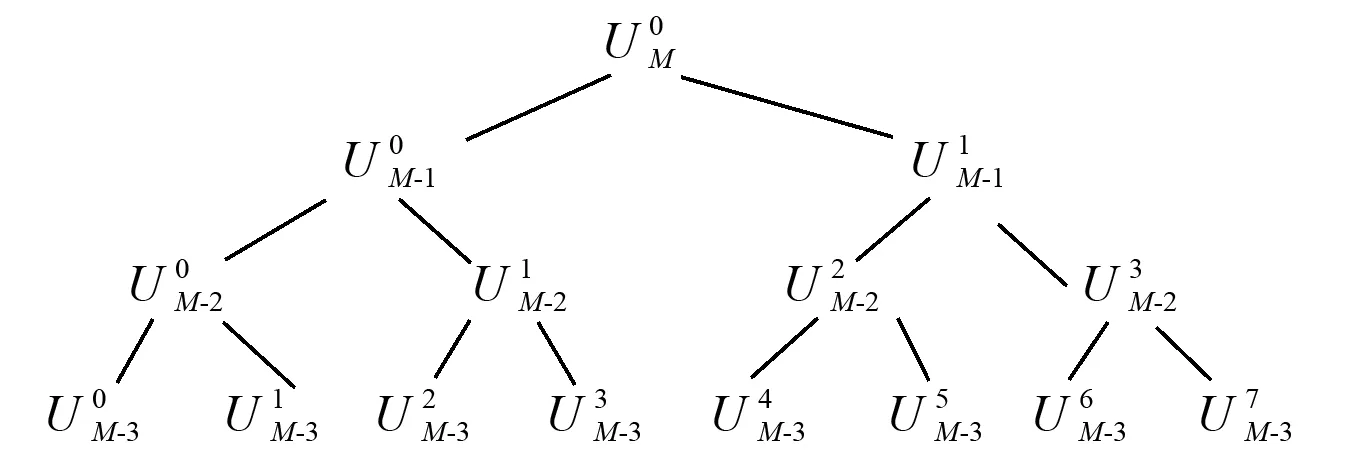
图1 小波包三层分解示意图Fig.1 Wavelet package decomposition of three layers schemes

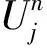
(1)

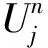
(2)

(3)

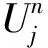
2 拉普拉斯特征值映射方法

拉普拉斯特征值映射(LE)[12]是一种非常有效的流形学习的算法。拉普拉斯特征值映射的基本思想是平均意义上保持数据点的邻近信息，即通过特征映射，原本在高维空间上距离接近的点在低维空间中的映射后也应该距离接近。以两个数据点之间的加权距离作为罚函数，利用图拉普拉斯算子进行求解。拉普拉斯特征值映射具有良好的算法保持性，具有对噪声不敏感，使用局部距离不易短路等优点。

LE算法可表述为以下三个步骤：

步骤1 构建近邻图。如果Xi和Xj是近邻点，可以在结点i和j之间置一条边，目前有ε-和K近邻两种方法。本文选用k=5的K近邻方法构建邻接图。

步骤2 确定边的权值Wij。边的权值的确定一般有两种方法：① 热核方法(Heat Kernel)，若第i个节点和第j个结点之间的是连接的，则定义边的权值：Wij=exp(-‖xi-xj‖2/σ2)，否则Wij=0；② 直接法，如果第i个和第j个节点之间有边连接，则定义边的权值为Wij=1，否则Wij=0。

步骤3 特征映射。假设前面所建立的邻接图是连通的，寻找低维的嵌入的问题实际上是对广义特征向量的求解

Ly=λDy

(4)

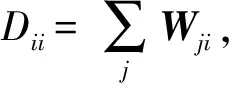
(5)

经过特征值分解得到的第2项～第d+1项的特征值对应的特征向量也就是算法的d维输出坐标。LE算法把问题转化为了特征值的求解，不需要迭代值的计算，所以只需要很少的计算量。

3 故障特征的提取方法

3.1 高维原始特征向量的形成

柱塞泵运行时的健康状态的识别的关键是通过对柱塞泵运行状态特征的提取。由于实验的设备复杂，所测得的振动信号中包含大量噪声数据和冗余信息，所以难以直接通过振动信号进行评估。借助于特征提取的方法，把原始信号变换到高维的特征空间中，进而通过对特征的分析掌握设备运行的健康状态。通过原始信号提取的时域，频域和时频混合域的参数已经被广泛使用，但是对于不同的设备对应采集信号的性质各不相同，甄选出具有较高分辨率和规律性强的特征参数是状态评估的关键。

本文采用常见的小波系数能量为计算特征向量的方法[13]，同时根据柱塞泵振动信号的特点，选取最大绝对均值，最小绝对均值，绝对均值，方差，峰度和偏度六个参数作为信号的时频信息，采用db6小波进行8层分解，得到全频带均匀划分的256个特征作为子频带滤波信号，将各子频带的能量作为频域的统计特征。表1所列的时域和频域的262个特征构成数据表示为X∈RN×m，其中N为样本数目，m为原始特征数，m=262。

表1 时域与频域特征参数表

3.2 特征向量的归一化处理

为了避免某些节点系数能量的绝对值过大导致在分析中造成偏差，一般需要对所得小波系数能量均进行规范化处理，使得各维度取值在一定范围内避免较大偏差，且方便连续算法处理。采用规范化方法z-score算法，其公式为

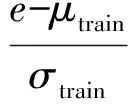
(6)

式中:μtrain为从某一训练集计算的均值；σtrain则是从同一训练集中计算的标准差。

3.3 基于拉普拉斯特征映射对特征的提取

柱塞泵系统的结构复杂，要获得精确的数学模型并不容易，因此模式识别是对柱塞泵的健康状态进行评估的有效方法。

在对故障样本进行特征提取后，再利用拉普拉斯特征向量良好的映射能力，对故障数据样本的特征进行相关，将故障样本特征映射到特征空间蕴涵的几何关系作为分类特征，进而识别故障的类别。本文通过k=5的K最近邻法(KNN)构建邻接图，使用热核法确定权值，进而使用局部线性投影和低维特征提取。

如图2所示，基于拉普拉斯特征向量柱塞泵诊断方法主要步骤为：

步骤1 从柱塞泵测试系统采集到的原始数据作为振动信号的样本空间；

步骤2 对信号进行预处理，分别提取振动信号时域、时频域的特征，共计262个特征参数，组成特征空间；

步骤3 选取特征空间的高维矩阵，对特征向量矩阵进行降维处理，选取的主要方法有LLE、LE、LPP、PCA(Principal Component Analysis)[14]、KPCA(Kernel Principal Component Analysis)[15-16]、Isomap[17-19]等；

步骤4 通过降维后的特征向量使用K最近邻算法进行分类，计算步骤4不同的降维方法获得的分类精度；

步骤5 评价不同降维方法的分类效果。

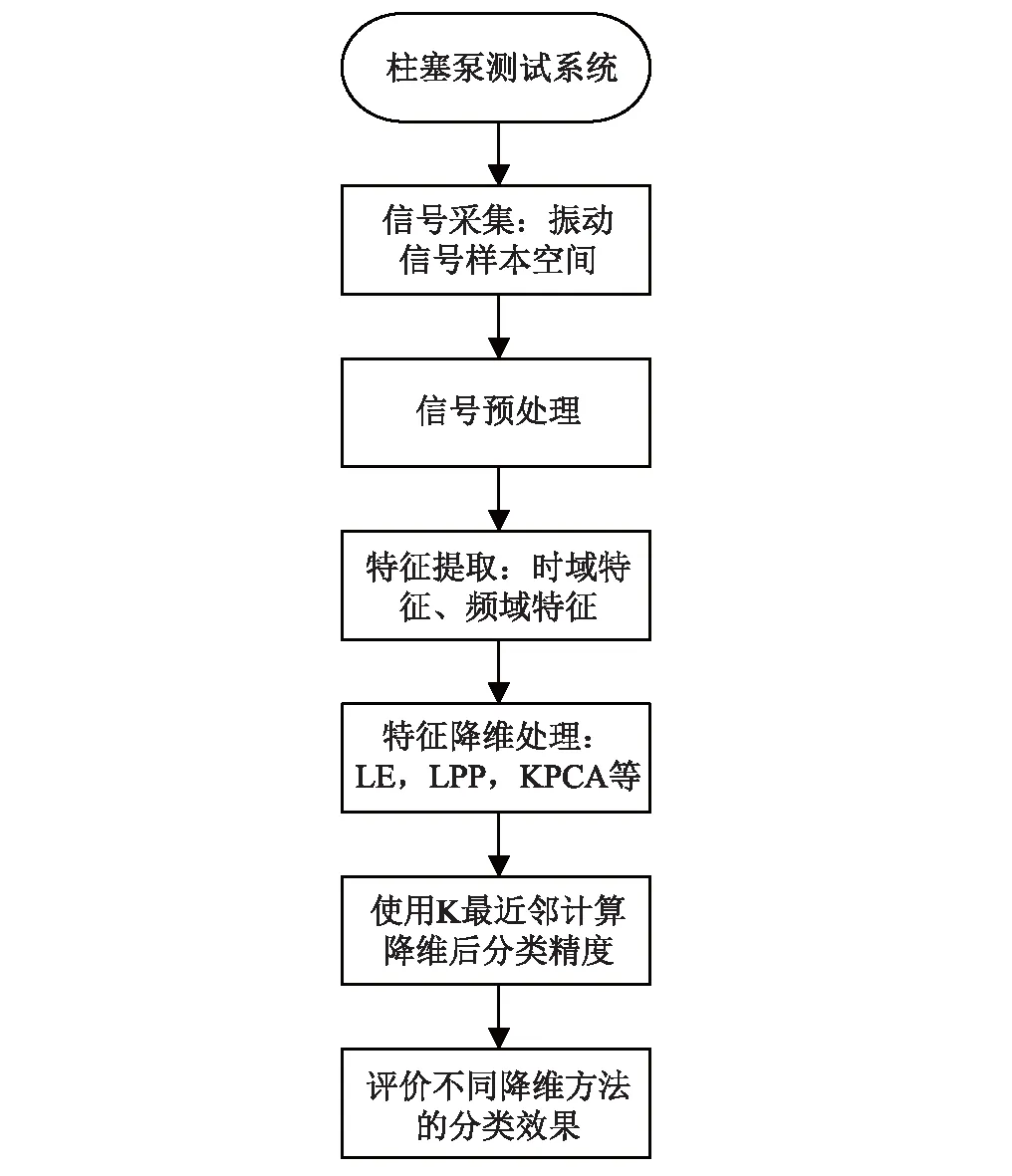
图2 健康评估方案流程Fig.2 Health assessment program flow

本文方法的最大优点在于通过对特征集的时域、频域和时频域特征的选择，得到了一组能够通过表征系统故障特性的特征向量，通过降维之后的低维矩阵进行健康状态分类，降低了分类的难度。

4 健康状态分类实验验证

本文中的柱塞泵测试系统参考国标“液压传动电控液压泵性能试验方法：GB/T 23253—2009 ”中的标准进行搭建。实验的对象为川崎K3V系列，是一种具有9个柱塞的斜盘式轴向柱塞泵。柱塞泵的压力脉动频率ω和柱塞泵的转速n成正比，ω=18πn/60 rad/s。实验选取1#～5#柱塞泵，在柱塞泵转速为2 200 r/min工况下运行800 s，泵的出口处的脉动频率为2 073.5 Hz。一般情况下，在柱塞泵保持运行状态时，很少会出现两种故障同时发生的情况，每次运转柱塞泵的故障所造成的压力冲击只有一次，于是柱塞泵的冲击频率为ω1=2πn/60 rad/s。当柱塞泵的转速为2 200 r/min时，故障特征频率的集中在230.4 Hz。柱塞泵的振动信号通过JX61G系列振动传感器测得。实验使用的振动传感器有3个，分别安装在柱塞后泵油泵出口处的左上、右上和正下方，任意两个传感器之间的夹角为120°。传感器的采样频率为50 kHz，满足奈奎斯特采样定理的要求。实验台搭建如图3所示。

图3 实验台系统Fig.3 Test-bed system

4.1 实验Ⅰ柱塞泵磨损情况验证

实验用的柱塞泵在前400 h是柱塞泵的磨合期，柱塞泵振动信号的性质变化较大。为了细化柱塞泵在前400 h的工作情况，我们分别选取1#，2#和4#作为柱塞泵的磨合期测试实验泵，选取5#作为正常工作(健康状态)的测试柱塞泵，选取3#作为即将报废的实验泵。表2对应柱塞泵的实际运行时间和简记代号。

实验中选取了工作时间最长的3#柱塞泵进行拆解，对应部件的磨损情况如图4所示。经过实际测量，可测得斜盘支撑座的最大磨损量为1.24 mm，最小磨损量为0.22 mm，而柱塞磨损量为0.06 mm。从图4(c)可以看出，斜盘支撑座的高压区的铜镀层已经磨尽，而低压区的铜镀层磨损量相对较少，表明即使是同一部件，由于工况不同造成不同位置的磨损量不同。

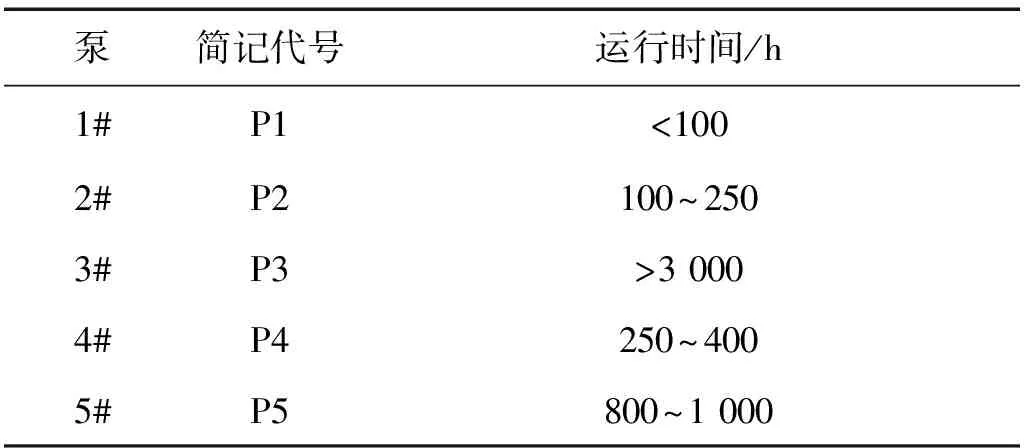
表2 柱塞泵代号

4.2 实验Ⅱ 不同柱塞泵健康状态评估实验

我们分别从P1、P2、P3、P4和P5柱塞泵选取了共500个数据样本点，其中每种状态样本各选100个数据样本点，特征空间维数为262，特征空间可以表示为X500×262。分别以LE、LPP、LLE、Isomap、PCA和KPCA算法对数据进行维数约简处理，转化到低维空间进行特征提取以进行模式识别分析。设参数的邻近因子k=5，使用最大似然估计计算嵌入维数d′=23。

图4 3#柱塞泵不同部件磨损情况Fig.4 3# wearing condition of different piston parts

如图5(a)所示，是拉普拉斯故障信号明显被分成了5类，类内距小，聚合明显，容易区分，其中P1和P2类间距较近，说明柱塞泵在前100 h和100～250 h的特征区别不明显，可以作为同一类型的健康状态处理。P3、P4和P5类间距大，类内距小，健康状态区别明显，P3和其他几类间距更大，区别明显。如图5(b)和图5(e)所示分别采用LPP和PCA方法进行分类，类间距大，样本分散，聚类性差。如图5(f)所示，采用KPCA方法进行分类，虽然使用了核函数方法使类内距变小，但是类间距小，分类效果差。如图5(c)和图5(d)所示，分别采用LLE方法和Isomap方法对数据进行降维，和LE方法同属非线性降维方法，特点是降维后类内距小，聚类效果优于线性降维方法，但是P4和P5类出现了不同程度的混叠，聚类效果也不如LE方法。

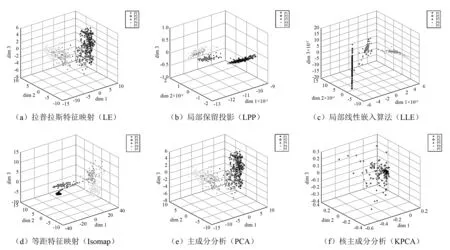
图5 柱塞泵1#～5#特征向量降维结果Fig.5 Feature vectors reduction results of piston 1#～5#

为了比较不同嵌入维数对分类精度的影响，我们计算了使用LE方法降维后的数据在不同嵌入维数的下的降维结果，然后计算出使用KNN作为分类器的辨识精度，实验结果如图6所示。实验结果表明，当嵌入维数23lt;d′≤262，此时特征维数较高，原始特征矩阵包含大量噪声等冗余信息，最小特征值对应的特征向量往往和噪声有关，降维能起到降噪的效果；当嵌入维数0lt;d′lt;23，此时特征维数较低，一定程度上损失了大量有用信息，此时的辨识率随着维数的不断下降而减少；使用最大似然估计计算嵌入维数d′=23获得最佳分类精度98.649%。

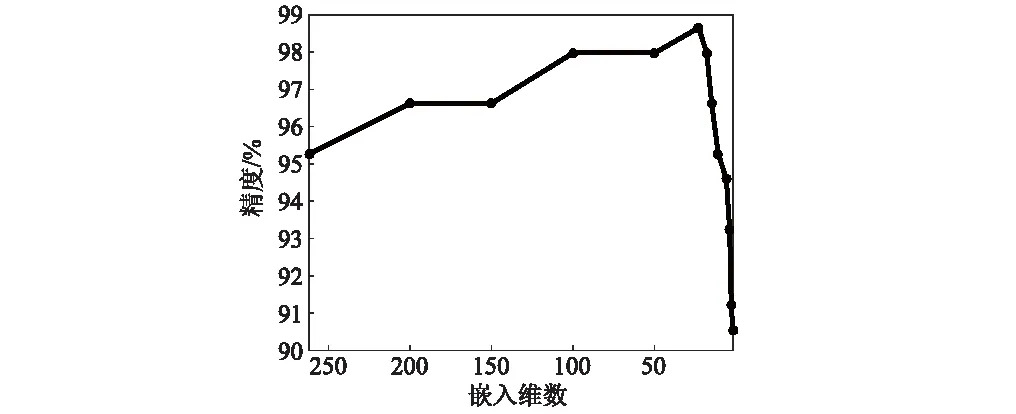
图6 不同嵌入维数下的分类精度Fig.6 Classification accuracy of different embedding dimension

为了评价不同降维方法对应的分类效果，我们选用K最近邻分类法验证模型分类精度。设置近邻因子k=5，把实验样本按照7∶3分为训练样本和测试样本两类，训练样本用于训练模型，利用测试样本数据来验证模型的准确性。不同降维方法对应模型的分类精度按10次平均计算，并由此获得最佳的效果。如表3所示，使用LE、LLE、KPCA等不同降维方法获得的降维结果经过K最近邻方法验证，比较不同验证模型的准确性，LE方法具有最高分类精度97.973%，表明使用LE方法对于柱塞泵的运行状态具有较高的区分性，评估最为准确。

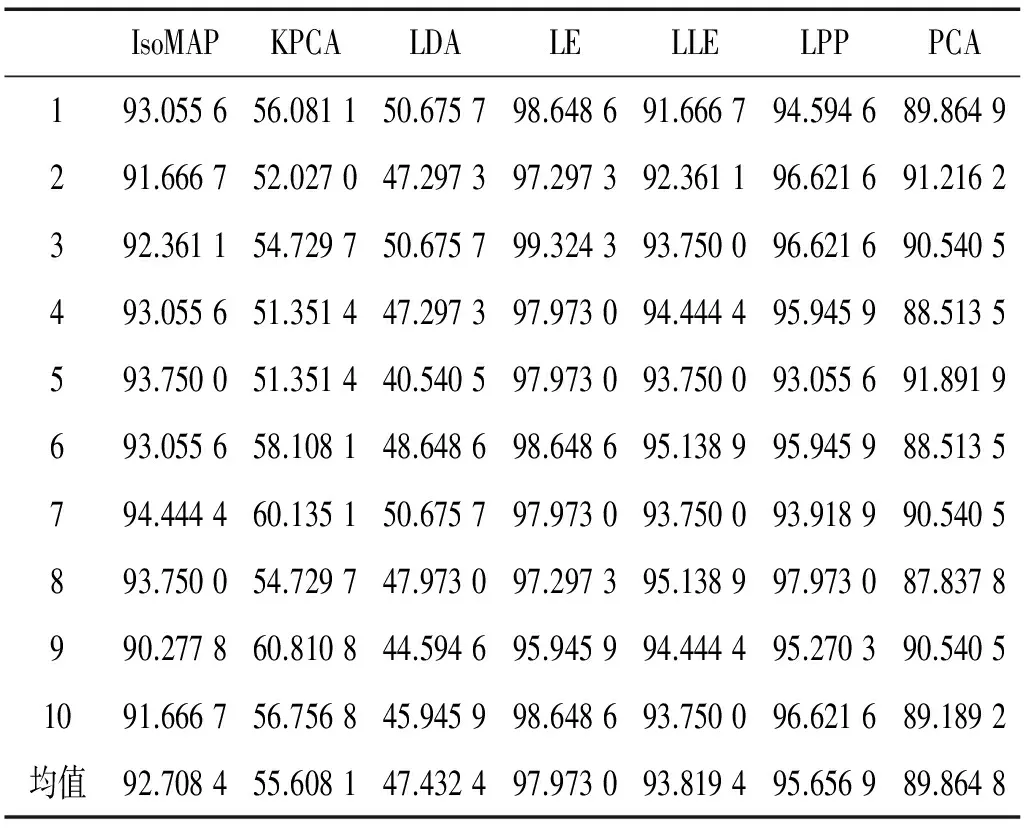
表3 柱塞泵1#～5#降维后的数据辨识结果

5 结 论

本文针对柱塞泵的健康评估问题，提出了一种基于小波包和拉普拉斯特征值映射的分析方法。该方法利用小波包对高频信号的分辨率高的特点，选取时域特征和小波包系数的能量作为特征，使用流形学习方法降维处理，并做出状态评估。分析实验结果表明：

(1) 对于柱塞泵柱塞泵健康状态评估方法，通过LE方法降维后的数据都具有更好的聚类性，状态识别的准确率比LPP、LLE、Isomap、PCA和KPCA等方法更高。通过对柱塞泵状态的准确评估，能对有可能产生的故障进行预防，具有重要的意义。

(2) 利用小波包对信号进行分解，能同时对高频和低频信号进行精细划分，再加上能表征信号特性的时域特征，实验表明，所选取的特征能较好地反映柱塞泵的状态信息，对柱塞泵的状态的评估具有重要作用。

(3) 在今后的工作中，将会采用不同型号的柱塞泵，分析验证该模型的准确性，同时使用在工程机械的实际应用场合，结合周围元件对柱塞泵的影响，验证实际工况下不同条件对液压泵健康状态的影响。

[ 1 ] 何正嘉，訾艳阳，孟庆丰．机械设备非平稳信号的故障诊断原理及应用[M]．北京：北京高等教育出版社，2001．

[ 2 ] DAUBECHIES I, BATES B J. Ten lectures on wavelets[J]. The Journal of the Acoustical Society of America, 1993, 93(3)： 1671.

[ 3 ] 高英杰，孔祥东. 基于小波包分析的液压泵状态监测方法[J]. 机械工程学报, 2009, 45(8)： 80-88.

GAO Yingjie, KONG Xiangdong. Wavelet packets analysis based method for hydraulic pump condition monitoring [J]. Journal of Mechanical Engineering, 2009, 45(8)： 80-88.

[ 4 ] ROWEIS S T, SAUL L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290： 2323-2326.

[ 5 ] TENENBAUM J B, SILVA V D, LANGFORD J C. A global geometric framework for nonlinear dimensionality reduction[J]. Science, 2000, 290： 2319-2323.

[ 6 ] 蒋全胜，贾民平，胡建中，等. 基于拉普拉斯特征映射的故障模式识别方法[J].系统仿真学报，2008，20(20)： 5710-5713.

JIANG Quansheng，JIA Minping，HU Jianzhong，et al. Method of fault pattern recognition based on Laplacian eigenmaps[J]. Journal of System Simulation，2008，20(20)：5710-5713.

[ 7 ] HE X，NIYOGI P. Locality preserving projections[M]. Cambridge: MIT Press，2003：153-160.

[ 8 ] 徐金梧，吕勇，王海峰. 局部投影算法及其在非线性时间序列分析中的应用[J]. 机械工程学报，2003，39(9)：146-150.

XU Jinwu, LÜ Yong, WANG Haifeng. Local projective method andit’s application onnonlinear time series[J]. Journal of Mechanical Engineering,2003,39(9)： 146-150.

[ 9 ] JIANG Quansheng，JIA Minping，HU Jianzhong，et al. Machinery fault diagnosis using supervised manifold learning[J]. Mechanical Systems and Signal Processing，2009，23(7)： 2301-2311.

[10] YU Jianbo. Local and non-local preserving projection for bearing defect classification and performance assessment[J]. IEEE Trans. Ind. Electron，2012，59(5)： 2363-2376.

[11] 王红军, 徐小力，万鹏. 基于轴心轨迹流形拓扑空间的转子系统故障诊断[J]. 机械工程学报, 2014, 50(5)： 95-101.

WANG Hongjun, XU Xiaoli, WAN Peng. Rotor system fault diagnosis based on orbit manifold topological[J]. Journal of Mechanical Engineering, 2014, 50(5)： 95-101.

[12] 黄宏臣，韩振南，张倩倩，等. 基于拉普拉斯特征映射的滚动轴承故障识别[J]. 振动与冲击, 2015, 34(5)： 128-134.

HUANG Hongchen,HAN Zhennan,ZHANG Qianqian, et al. A method for fault diagnosis of rolling bearings based on laplacian eigenmap[J]. Journal of Vibration and Shock, 2015, 34(5)： 128-134.

[13] 丁晓喜，何清波. 基于WPD和LPP的设备故障诊断方法研究[J].振动与冲击, 2014, 33(3)： 89-93.

DING Xiaoxi, HE Qingbo. Machine fault diagnosis based on WPD and LPP[J]. Journal of Vibration and Shock, 2014, 33(3)： 89-93.

[14] 高东，吴重光，张贝克，等. 基于PCA和SDG的传感器故障诊断方法研究及应用[J].系统仿真学报, 2011， 23(3)： 567-573.

GAO Dong, WU Chongguang, ZHANG Beike, et al. Method combining PCA and SDG for fault diagnosisof sensors and its application[J]. Journal of System Simulation, 2011, 23(3)： 567-573.

[15] XU Yong, ZHANG D, SONG F, et al. A method for speeding up feature extraction based on KPCA[J]. Neurocomputing, 2007, 70(4/5/6)： 1056-1061.

[16] 杨先勇，周晓军，张文斌，等. 基于局域波法和 KPCA-LSSVM的滚动轴承故障诊断[J]. 浙江大学学报(工学版), 2010， 44(8)：1519-1524.

YANG Xianyong, ZHOU Xiaojun, ZHANG Wenbin, et al. Rolling bearing fault diagnosis based on local wave methodand KPCA-LSSVM[J]. Journal of Zhejiang University (Engineering Science), 2010, 44(8)： 1519-1524.

[17] BALASUBRAMANIAN M, SCHWARTZ E L. The isomap algorithm and topological stability[J]. Science, 2002, 295： 7.

[18] 孟德宇，徐晨，徐宗本. 基于Isomap的流形结构重建方法[J]. 计算机学报, 2010, 33(3)： 545-555.

MENG Deyu, XU Chen, XU Zongben. A new manifold reconstruction method based on Isomap[J]. Chinese Journal of Computers, 2010, 33(3)： 545-555.

[19] 刘爱萍, 王洪元, 程起才, 等. 基于KISOMAP-LDA-KNN算法TE过程故障诊断研究[J]. 计算机与数字工程, 2010, 38(11)： 34-37.

LIU Aiping, WANG Hongyuan, CHENG Qicai, et al. An algorithm of KISOMAP-LDA-KNN for the research of the fault diagnosis of TE process[J]. Computer and Digital Engineering, 2010, 38(11)： 34-37.

HealthassessmentforapistonpumpbasedonWPDandLE

WANG Haoren1, HUANG Yixiang1, ZHAO Shuai1, LIU Chengliang1, WANG Shuangyuan1, ZHANG Daqing2

(1.State Key Laboratory of Mechanical System and Vibration, Shanghai Jiao Tong University, Shanghai 200240, China;2. Sunward Intelligent Equipment Group, Changsha 410100, China)

A piston pump is one of the key components in a hydraulic system, monitoring its health condition is of significant importance for reliable performance of the hydraulic system. Therefore, a health state evaluation method was proposed based on the wavelet packet decomposition (WPD) and the manifold learning by analyzing the vibration signals at the piston outlet. The wavelet packet method was used to decompose original signals and effectively extract health state features group from them. The high dimensional feature group was set as an input and multiple manifold learning methods were conducted and compared for dimensional reduction. The Laplacian eigenmaps (LE) method of the highest accuracy was used to establish a relationship between feature vectors and health states, which achieved the aim of health state classification. It is shown that the combination of the wavelet packet decomposition and the manifold learning method improve the accuracy of piston pump health state evaluation.

wavelet packet analysis; manifold learning; piston pump; Laplacian eigenmaps; health state evaluation

国家科技支撑计划(2014BAA04B01)；国家自然科学基金(51305258)；上海市科委项目(1411104600)

2015-12-10 修改稿收到日期： 2016-09-14

王浩任 男，博士生，1991年生

黄亦翔 男，博士，讲师，1980年生

TP306

A

10.13465/j.cnki.jvs.2017.22.008