充填体的分数阶微积分蠕变本构模型及其在FLAC3D中的开发应用
郭瑞凯,丁建华,赵 奎,谷睿智
(江西理工大学 资源与环境工程学院,江西 赣州 341000)
充填体的分数阶微积分蠕变本构模型及其在FLAC3D中的开发应用
郭瑞凯,丁建华,赵 奎,谷睿智
(江西理工大学 资源与环境工程学院,江西 赣州 341000)
为了更加准确地评估分析充填采矿法中实际矿山充填体矿柱的稳定性,通过在广义开尔文体中引入分数阶黏性元件来模拟胶结充填体蠕变过程,根据试验数据对所得蠕变本构方程利用爬山算法和全局优化法相结合的方式进行参数辨识,并将得到的蠕变本构方程开发进岩土数值分析软件FLAC3D中进行数值计算。计算结果表明,改进后的分数阶蠕变本构方程很好地拟合了试验数据,证明了改进模型及其计算程序的正确性。该成果对矿山矿柱充填及稳定分析具有实际指导意义。
胶结充填体;分数阶微积分;蠕变本构模型;爬山算法;FLAC3D二次开发
0 引言
随着对能源需求量的增加以及矿山开采强度的不断加大,地表和地下浅部矿产资源逐渐减少,国内外矿山开始逐渐进入资源的深部开采[1]。充填体采矿法可以很好地控制地表的沉陷,解决因地下开采引起的一系列难题[2],同时在降低矿石损失贫化等方面也具有显著的优势。有学者预测充填采矿法将成为21世纪最具潜力的采矿方法[3],因此充填采矿法将被金属矿山广泛使用。近年来,地下矿山的开采深度和强度在不断增大,充填体的蠕变特性越来越受到重视,有关充填体蠕变特性的研究产生了大量的成果,赵奎等[4]将充填体制成直径50 mm×100 mm的试样,并在实验室进行单轴蠕变试验,同时利用Hoek-Kelvin模型来描述充填体的蠕变特性,将模型嵌入进FLAC3D软件中,很好地模拟了胶结充填体的蠕变特性。马乾天等[5]通过单轴压缩试验研究块石胶结充填体的失稳方式,并利用基于颗粒流理论的PFC程序对充填体蠕变进行模拟,模拟结果与试验结果吻合良好。赵树果等[6]对充填体进行单轴分级蠕变试验,并通过引入Burgers模型来描述其蠕变特性,结果表明蠕变理论曲线很好地吻合了试验曲线。
目前对充填体蠕变本构模型的研究大都采用传统整数阶元件组合的方式,然而对用分数阶流变元件组合来模拟充填体蠕变特性的研究仅有少量研究成果。分数阶微分方程是将传统微分方程中整数阶次用分数来替代,相比整数阶微积分,分数阶微积分能够更好地拟合自然界中某些物理系统的动态过程和记忆过程,因此逐渐有学者开始将分数阶微积分引入到材料流变特性的研究当中。Y Kawada[7]等研究了岩石和矿物黏弹性行为,并基于分数阶微积分用分数阶导数代表时间的延迟程度推导出其本构方程。陈静[8]基于分数阶微积分并结合岩石蠕变过程中的损伤效应推导出花岗岩的蠕变本构方程,并将研究成果应用于锦屏水电站地下洞室群围岩长期稳定性研究。吴斐[9]通过引入分数阶非线性黏壶元件较好地描述了岩盐的蠕变全过程。
综上所述,利用改进的分数阶流变元件来模拟充填体的流变性质具有一定的实际意义。本文通过研究矿山采场充填体的蠕变特性,基于分数阶微积分推导出充填体在单轴加载下的蠕变本构方程,并将得到蠕变本构方程开发进岩土数值分析软件FLAC3D中,对得到的充填体蠕变模型进行蠕变试验数值模拟,研究结果可应用于矿山充填体矿柱的稳定性分析。
1 蠕变试验和蠕变模型
1.1 蠕变试验
试验所用水泥和尾砂皆来自武山某矿,其中水泥和尾砂的配比为1∶20,将其浇注成50 mm×100 mm的圆柱,并将其置于自制的简易分级增量循环加卸载装置上进行单轴加载,按照其事先测定的单轴抗压强度 1.5MPa,将其分成 210kPa、436kPa、662kPa、939 kPa、1 191 kPa五个级别进行分级加载。加载过程中当位移增量小于0.001 mm/h时,切换到下一个加载级别。加载得到的时间-应变曲线如图1所示。

图1 单轴分级加载下充填体时间-应变曲线Fig.1 Time-strain curve of filling body under uniaxial loading
由图1可知充填体不同于普通岩石的脆性破坏、塑性破坏以及弱面剪切破坏,充填体表现出明显的黏塑性特性,该类型蠕变形式存在明显的减速蠕变和等速蠕变阶段,无明显的加速蠕变阶段[10]。
1.2 蠕变模型
传统的广义开尔文体由一个弹簧体和一个开尔文体串联组成,其力学模型如图2所示。
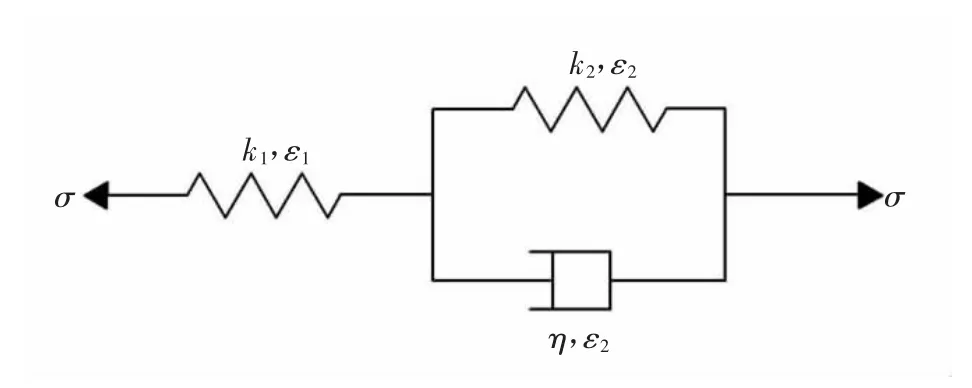
图2 广义开尔文体模型Fig.2 The generalized Kelvin model
图2 中σ为应力,MPa;k1和k2表示弹簧的弹性元件弹性参数,GPa;η表示黏壶的牛顿黏性系数,GPa·h;其蠕变方程如式(1)所示。

本文在广义开尔文体模型的基础上,引入一个改进的分数阶微积分黏性元件,该元件用于描述充填体蠕变过程中处于弹性和黏弹性之间的状态,并反映蠕变过程中时效性。改进之后的模型如图3所示。

图3 改进后的广义开尔文体模型Fig.3 The modified generalized Kelvin model
有关分数阶微积分的定义主要有三种,分别是Grümwald-Letnikov 定义、Riemann-Liouville 定义和Caputo定义,试验研究中选择最常用的Riemann-Liouville定义。Riemann-Liouville对分数阶导数的定义如式(2)所示。

其中Γ(n-α)为伽马函数,伽马函数的定义是:

吴斐等[11]根据Riemann-Liouville定义推导出分数阶黏性元件的应变与时间的关系如式(4)所示。

因此改进后的充填体蠕变本构方程见式(5)。

其中,k1、k2为弹性元件的弹性参数,GPa;η1、η2分别为改进黏性元件和传统黏性元件的黏性系数,GPa·h;β表示分数阶次,且 0≤β≤1;t为蠕变时间,s。
2 参数识别
有关本构模型参数辨识的研究有很多,常见的有最小二乘法、遗传算法、神经网络法等,本试验选择比较简单但效率较高的爬山算法。爬山算法是通过模拟现实中的爬山过程,开始随机选取一个值进行逼近,每次都在选定值的临近的空间中选择最优解作为当前解,直到局部最优解。其爬山算法存在的缺点是比较容易在辨识过程中陷入局部最优解,而局部最优解并不一定满足全局最优解。因此本研究借助七维高科有限公司(7D-Soft High Technology Inc.)开发的优化分析软件1stOpt,通过应用爬山算法并结合1stOpt软件内嵌的通用全局优化法对蠕变本构方程(5)进行参数辨识,克服了爬山算法的不足,辨识结果见表1。
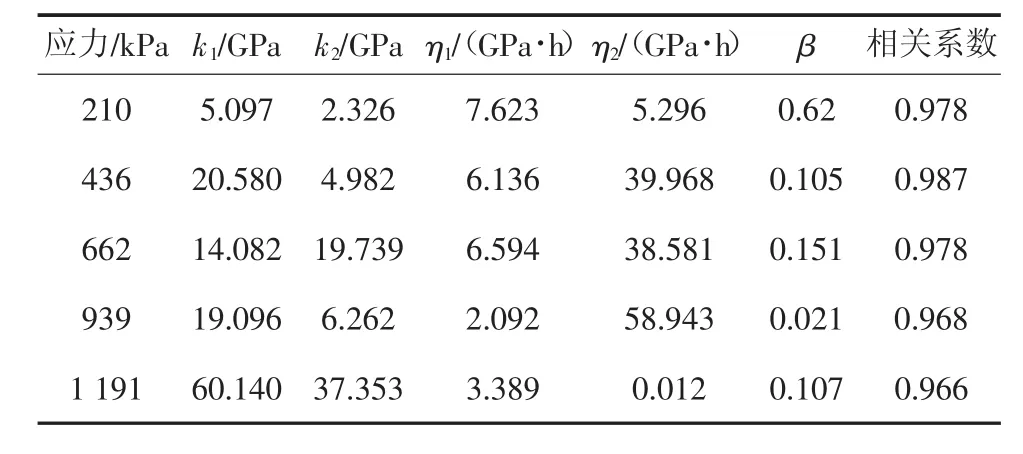
表1 改进模型拟合参数Tab.1 Fitting parameters of the modified model
3 蠕变本构模型在FLAC3D中的开发与实现
将自定义的蠕变本构模型开发进FLAC3D中需要将式(5)转化成三维的有限差分形式,研究根据陈静[2]推导的结果得出充填体蠕变本构方程的三维有限差分形式如式(6)所示。


式中:


式中:

式中:GM表示有弹性元件和改进黏性元件组成的类Maxwell体的剪切模量。
借助岩土数值分析软件FLAC3D预留的端口,在Visual Studio 2010中进行充填体蠕变本构模型的编写,编写内容主要包括头文件Gamma函数、基类Constituive Model等,其中式(6)、(7)和(8)将被编写进基类ConstituiveModel的成员函数run()中,生成可供FLAC3D计算调用的dll.文件,并将该文件嵌入到FLAC3D软件包中,在计算过程中通过config cppudm命令即可对蠕变模型进行调用。具体内容许多文献[12-16]已经报道,本文不再赘述。
数值计算模型为与试验试件相同尺寸的圆柱,如图2所示,模拟蠕变过程中利用FLAC3D内嵌的fish语言编写时步函数time_fun,计算过程中模型底部在y轴方向上施加约束,模型顶部施加垂直载荷,因模拟单轴加载,故模型侧向不施加约束,蠕变分析时步设置为1×10-3,监测点为圆柱顶部的中心原点。

图4 数值计算模型Fig.4 Model of numerical calculation
4 数值模拟计算结果与试验数据的对比
FLAC3D模拟结果如图5所示,将数值计算结果从FLAC3D中导出并与试验值进行对比,由图5和图6可知,数值计算结果很好地拟合了充填体的减速和等速蠕变阶段,证实了本试验所开发程序的正确性。

图5 FLAC3D模拟充填体分级加载Fig.5 Hierarchical loading of FLAC3Dsimulated filling body
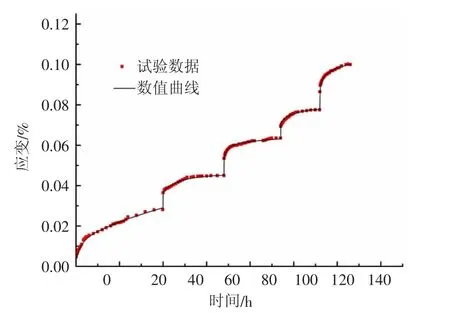
图6 模拟数据与试验数据对比Fig.6 Comparison between simulated data and experimental data
5 结论
通过试验与数值模拟相结合,通过二次开发,使理论得到的该配比下充填体分数阶微积分蠕变本构方程更好地应用于实际矿山中充填体矿柱的稳定性分析,得出以下结论:
(1)该配比下的胶结充填体具有显著的黏塑性特征,存在明显的减速蠕变和等速蠕变阶段。
(2)利用拟合软件1stOpt中内嵌的爬山算法和全局优化法对改进的蠕变本构方程进行参数辨识,辨识结果表明拟合参数合理有效,因此将爬山算法与全局优化法相结合可以提高其精度和寻优速度,对于参数辨识具有一定的意义。
(3)将数值计算结果与试验结果进行对比,发现改进的分数阶蠕变本构方程可以较好地拟合该配比下充填体的蠕变过程,并体现出了蠕变过程的时效性,从而证实了所开发模型的适应性和正确性。
[1] 何满潮,谢和平,彭苏萍,等.深部开采岩体力学研究[J].岩石力学与工程学报,2005,24(16):2803-2813.HE Manchao,XIE Heping,PENG Suping,et al.Study on rock mechanics in deep mining engineering[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(16):2803-2813.
[2] 史俊伟,陈章良,孙玉峰,等.充填开采控制地表沉陷可靠性模糊综合评判[J].中国钨业,2015,30(4):21-26.SHI Junwei,CHEN Zhangliang,SUN Yufeng,etal.Fuzzy comprehensive evaluation of reliability of surface subsidence control by filling mining[J].China Tungsten Industry,2015,30(4):21-26.
[3] 胡 华,崔明义.高水材料硬化体特性及其充填体力学作用机理分析[J].矿业研究与开发,2001,21(5):23-25.HU Hua,CUI Mingyi.Characteristics of high water content hardening body and analysis on the mechanical mechanism of fill body[J].Mining Research and Development,2001,21(5):23-25.
[4] 赵 奎,何 文,熊良宵,等.尾砂胶结充填体蠕变模型及在FLAC3D二次开发中的实验研究 [J].岩土力学,2012(增刊1):112-116.ZHAO Kui,HE Wen,XIONG Liangxiao,et al.Testing study of creep model for tailing cemented backfill and its secondary development based on FLAC3D[J].Rock and Soil Mechanics,2012(supply1):112-116.
[5] 马乾天,张东炜.基于颗粒流的块石胶结充填体短时蠕变特性研究[J].矿业研究与开发,2015(7):68-71.MA Qiantian,ZHANG Dongwei.Study on short-time creep characteristics of rocky cemented filling body based on PFC[J].Mining Research and Development,2015(7):68-71.
[6] 赵树果,苏东良,邹 威.充填体分级加载蠕变试验及模型参数智能辨识[J].矿业研究与开发,2016,36(6):54-57.ZHAO Shuguo,SU Dongliang,ZOU Wei.Study on creep properties of backfill under step loading and intelligent identification of constitutivemodelparameters[J].MiningResearchandDevelopment,2016,36(6):54-57.
[7] KAWADA Y,YAJIMA T,NAGAHAMA H.Fractional-order derivative and time-dependent viscoelastic behaviour of rocks and minerals[J].Acta Geophysica,2013,61(6):1690-1702.
[8] 陈 静.硬岩时效变形和破坏机制及其工程行为分析 [D].北京:中国科学院大学,2013.CHEN Jing.Time-dependent deformation and fracture mechanisms of hard rock and engineering behavioural analysis[D].Beijing:The University of Chinese Academy of Sciences,2013.
[9] 吴 斐,谢和平,刘建锋,等.分数阶黏弹塑性蠕变模型试验研究[J].岩石力学与工程学报,2014,33(5):964-970.WU Fei,XIE Heping,LIU Jiangfeng,et al.Experimental study of fractional viscoelastic-plastic creep model[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(5):964-970.
[10] 杨 欣.充填体蠕变本构模型及其工程应用[D].赣州:江西理工大学,2011.YANG Xin.Creep constitutive model of filling body and its engineering application[D].Ganzhou:Jiangxi University of Science and Technology,2011.
[11] 吴 斐,刘建锋,武志德,等.盐岩的分数阶非线性蠕变本构模型[J].岩土力学,2014,35(增刊 2):162-167.WU Fei,LIU Jianfeng,WU Zhide,et al.Fractional nonlinear creep constitutive model of salt rock [J].Rock and Soil Mechanics,2014,35(supply2):162-167.
[12] 蓝 航,姚建国,张华兴,等.基于FLAC3D的节理岩体采动损伤本构模型的开发及应用[J].岩石力学与工程学报,2008,27(3):572-579.LAN Hang,YAO Jianguo,ZHANG Huaxing,et al.Development and application of constitutive model of jointed rock mass damage due to mining based on FLAC3D[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(3):572-579.
[13] 陈育民,徐鼎平.FLAC/FLAC3D基础与工程实例[M].北京:中国水利水电出版社,2009.
[14] 周宏伟,王春萍,段志强,等.基于分数阶导数的盐岩流变本构模型[J].中国科学:物理学 力学 天文学,2012,42(3):310-318.ZHOUHongwei,WANGChunping,DUANZhiqiang,etal.Rheological constitutive model of salt rock based on fractional derivative[J].Scientia Sinica Physica,Mechanicaamp;Astronomica,2012,42(3):310-318.
[15]朱晓鹏.基于节理岩体损伤本构模型的FLAC3D二次开发及应用[D].北京:中国地质大学,2015.ZHU Xiaopeng.The secondary development of FLAC3DBased on Jointed rock mass damage model and its application[D].Beijing:China University of Geosciences,2015.
[16] 高文华,刘 正,张志敏.基于FLAC3D的粉砂岩压缩蠕变试验数值模拟研究[J].土木工程学报,2015(3):96-102.GAO Wenhua,LIU Zheng,ZHANG Zhimin.Numerical simulation study on compression creep experiment of siltstone based on FLAC3D[J].China Civil Engineering Journal,2015(3):96-102.
Fractional Calculus Creep Constitutive Model of Filling Body and its Development and Application in FLAC3D
GUO Ruikai,DING Jianhua,ZHAO Kui,GU Ruizhi
(Faculty of Resources and Environmental Engineering,Jiangxi University of Science and Technology,Ganzhou 341000,Jiangxi,China)
For an accurate analysis on the stability of filling pillars,this paper simulated the creeping process of cemented backfill by applying fractional viscous components in the generalized Kelvin system.Parameters were identified on the creep constitutive equation by combining Hill Climbing algorithm and global optimization method.The creep constitutive equation is developed into numerical analysis software FLAC3Dfor rock and soil numerical calculation.The calculated results show that the modified fractional creep constitutive equation fits the experimental data well,which testifies the correctness of the improved model and its calculation program.
cemented filling body;fractional calculus;creep constitutive model;hill climbing algorithm;FLAC3Dsecondary exploration
TD853;TU443
A
10.3969/j.issn.1009-0622.2017.05.005
2017-08-28
江西省科技计划项目(20143ACG70010);江西省主要学科学术和技术带头人培养计划(20153BCB22004);江西省“5511”优势科技创新团队(20165BCB19012)
郭瑞凯(1990-),男,河北邢台人,硕士,主要从事岩石力学方面的研究。
赵 奎(1969-),男,安徽六安人,教授,主要从事岩石力学测试技术方面的研究。
(编辑:游航英)

