芳香胺固化环氧树脂非等温DSC动力学的研究

张思思，周茗萱，李文翔，吴攀洛，管 蓉

（湖北大学化学化工学院，湖北 武汉 430062）

芳香胺固化环氧树脂非等温DSC动力学的研究

张思思，周茗萱，李文翔，吴攀洛，管 蓉

（湖北大学化学化工学院，湖北 武汉 430062）

基于非等温DSC得到的数据，采用唯像模型法及非模型法研究了环氧树脂/芳香胺固化体系的固化动力学。唯像模型法中，通过对固化曲线及Málek法引入的y（α），z（α）曲线分析，预测了该固化体系符合SB双参数自催化模型，并使用Levenberg-Marquardt（LM）算法进行最小二乘拟合，引入动力学修正因子Cf进 行修正拟合；非模型法中，使用改进的等转化率法（NLV Vyazovkin法）计算了不同固化度（α）条件下活化能（Eα）的大小，通过ABS微分法对几组简化的SB方程进行了补偿参数计算。结果表明，引入Cf的 SB双参数自催化模型能够较好地拟合该固化体系固化反应动力学过程；反应前期Eα随α增加而快速下降，固化反应后期Eα又逐渐增加；Eα与指前因子（A）之间的关系能够通过“补偿参数”方程进行较好的表达。

环氧树脂；固化动力学；修正模型法；改进等转化率法；补偿参数法

环氧树脂基复合材料在军事工业，航空航天及电子工业等方面应用十分广泛。随着环氧树脂基复合材料使用范围逐渐拓展、围绕环氧树脂复合界面及固化反应对复合材料最终性能影响的研究逐渐深入[1，2]，从中发现固化动力学是深入研究环氧树脂交联固化形成稳定三维网络过程的重要手段，对于调控交联网络结构，提高复合材料性能十分关键[3]。环氧树脂固化反应动力学过程十分复杂，导致其复杂性的原因有多个方面：一是固化机理的内在复杂性，固化反应中可能发生多种引发、多步终止以及链增长的复杂竞争；二是交联网络形成过程的复杂性，随着固化的推进，分子质量、支化程度在增加，凝胶及玻璃化出现，都对支化交联网络的形成带来较大的影响[4]。固化过程的复杂性对于动力学的研究提出了更高的要求，这种要求体现在先进的测试手段和科学的动力学数据处理这2个方面。本研究采用非等温DSC法获取动力学参数，利用唯像模型法及非模型法，通过多重数学分析手段，全面分析环氧树脂/芳香胺体系固化动力学过程，构建了动力学修正模型，并建立了动力学因子之间的函数关系，以期为环氧树脂固化动力学的研究提供理论依据及数学分析方面的重要参考。

1 实验部分

1.1 实验原料及仪器

环氧树脂（E-51、环氧值为0.49～0.52），岳阳石化股份有限公司；改性间苯二胺固化剂（GT-5），湖北奥生新材料有限公司。

DSC200 F3型差示扫描量热仪，德国耐驰公司。

1.2 DSC测试程序

先 控 制 m（固 化 剂 GT-5）∶ m（E-51）=35∶100[5]。

DSC扫描前使用超微电子天平称取5～7 mg样品至铝样品坩埚中，盖上盖子后迅速放入样品池中，分别以5、7.5、10、15、20 K/min在-20～280 ℃内进行等速升温测试，然后迅速降温至0 ℃，再以10 K/min升温至280 ℃确认固化完全并测定玻璃化转变温度（Tg）。测试过程中使用高纯N2保护，N2流量为40 mL/min。

2 结果与讨论

2.1 动态扫描过程分析

不同升温速率下DSC热流对时间的关系如图1a所示。由图1a可知：该固化体系固化反应呈现明显的固化延迟行为。选择水平基

线，对热流时间进行积分，可以得到不同升温速率下的固化反应热△HTotal。 不同升温速率下的固化曲线还可以转化为热流温度曲线，按照ASTM E2041[6]标准，固化的凝胶温度（Tonset） 、后固化温度（Tendset）以及峰值温度（Tp）可以根据热流温度曲线得到。二次扫描后，按照ASTM E2602[7]标准可以得出Tg。 以上基本动力学参数均列于表1中。表1还列出了固化峰值温度时的固化度αp及 峰值固化速率（dα/dt）p、 （dα/dT）p。

2.2 动力学模型的预测和分析

动力学分析过程实际是对固化速率过程的量化，动力学分析都是以方程（1）为基础的[8]。

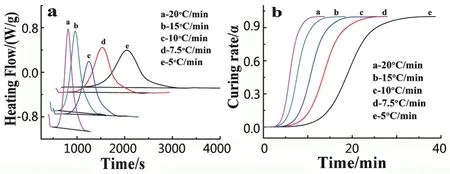
图1 （a）不同升温速率下热流对时间关系图；（b）不同升温速率下固化度对时间关系图Fig.1 a.Heating flow at different heating rates versus time，b.Curing degree at different heating rates versus time

表1 固化反应基本动力学参数Tab.1 Basic kinetic parameters of curing reactions

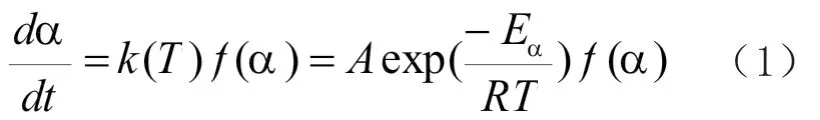
式中：α为固化度，t为时间，T为温度，k（T）为反应速率常数，且遵循阿伦尼乌斯方程，f（α）为固化机理函数，A为指前因子，Eα为表观活化能，R为气体常数，R=8.3145 J·mol/K。对于恒定升温速率β=dT/dt的固化过程，一般使用方程（2）进行固化动力学的处理。

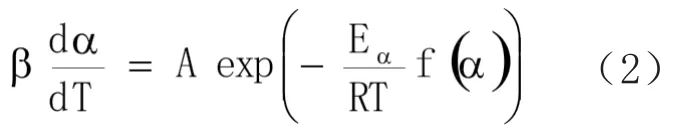
目前，环氧树脂固化动力学研究领域可根据固化机理函数f（α）形式特点，将不同固化动力学模型主要分为n级反应模型和自动催化模型[4]。 根据Yousefi等[9]对不同固化模型特点分析及ICTAC[10]关于不同固化反应模型α-T图形的归纳，对得到的“S”型α-T图（图1b）分析可以预测反应模型为自催化模型，对于该体系的具体固化模型可以根据Má lek[11]法 进行进一步的确定。Málek[12]定义的2个特殊方程y（α）及z（α）如式3和式4所示。

通过对y（α）及z（α）图形进行分析认为，可以采用合理的模型对固化过程进行描述，上述2式中X=Eα/RT，Salvador Montserrat[12]认为，可以使用Senum和Yang提出的近似式[13]来表示π（X）（见式5）。

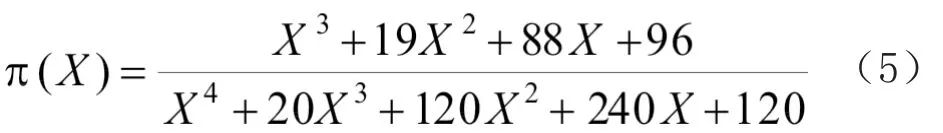
用计算得到的平均活化能Eα值（在后面的计算中得到）就能够得到y（α）、z（α）值，将其标准化在[0，1]范围内做y（α）及z（α）对α的关系曲线，如图2所示。

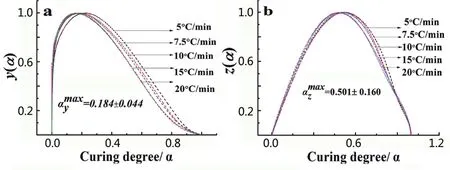
图2 a为y（α）对α关系曲线，b为z（α）对α关系曲线Fig.2 a Curves for y（α）versus α，b curves for z（α）versus α

当处于固化峰值温度时，固化速率的导数等于0，也就是说固化度是关于温度的常数而与升温速率无关，根据Sun等[15]的报道可以对上面公式进行近似处理得到方程式（8）。

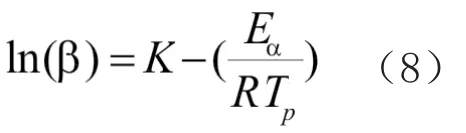
式中：Tp为 峰值固化温度，对方程（8）进行线性拟合，根据斜率可以计算得到Eα，具体数值均列于表2中。根据截距得到K，K还可以表达为式（9）。

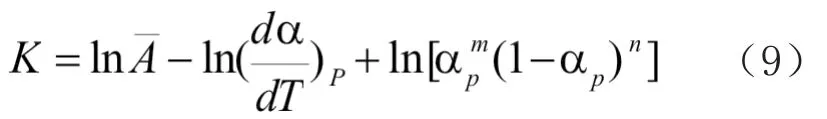
式中：（dα/dT）p为 峰值相对于温度的固化速率，αp为 相对最大固化速率时的固化度，具体值在表1中给出，代表5个升温速率下的指前因子平均值，对式（9）进行变换和整理可以得到式（10）。

根据文献[5，15，16]报道，在得到平均指前因子后，可以通过引入修正因子Cf进 行修正并计算出与升温速率有关的指前因子Af， 方程如式（11）所示。

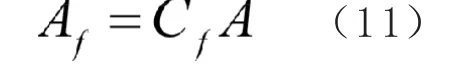
将方程（10）、（11）及机理函数方程（6）代入方程（1），整理可以得到固化速率方程（12）。

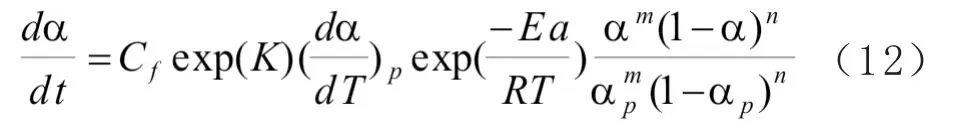
修正因子Cf， 反应级数m、n可以使用基于LM算法进行最小二乘拟合得出，结果列于表2中。

2.3 拟合结果

整个固化过程的拟合使用平均指前因子和平均表观活化能进行计算，在确定出A、Eα、m及n后，对α与T之间的关系方程（13）进行积分可以得到固化度与温度之间的关系，为保证积分结果的精确，这里使用了四阶Runge-Kutta法进行积分计算。结果如图3a所示，其中a为实验数据，b为修正前的拟合数据，c为修正后的拟合数据。由图3可知：引入修正因子后的拟合结果更加接近于原始实验数据结果，拟合效果更佳。

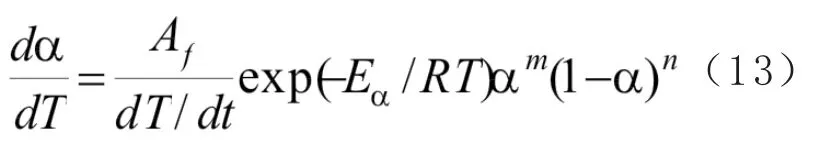
图3b为5个不同升温速率下固化反应速率与反应温度之间的拟合关系图，图中实线代表实验数据，间断线代表模型拟合数据，间断点线代表修正模型拟合数据，图3b能够得出与图3a相同的结论，修正后的拟合结果优于修正前，且更加逼近实验数据。

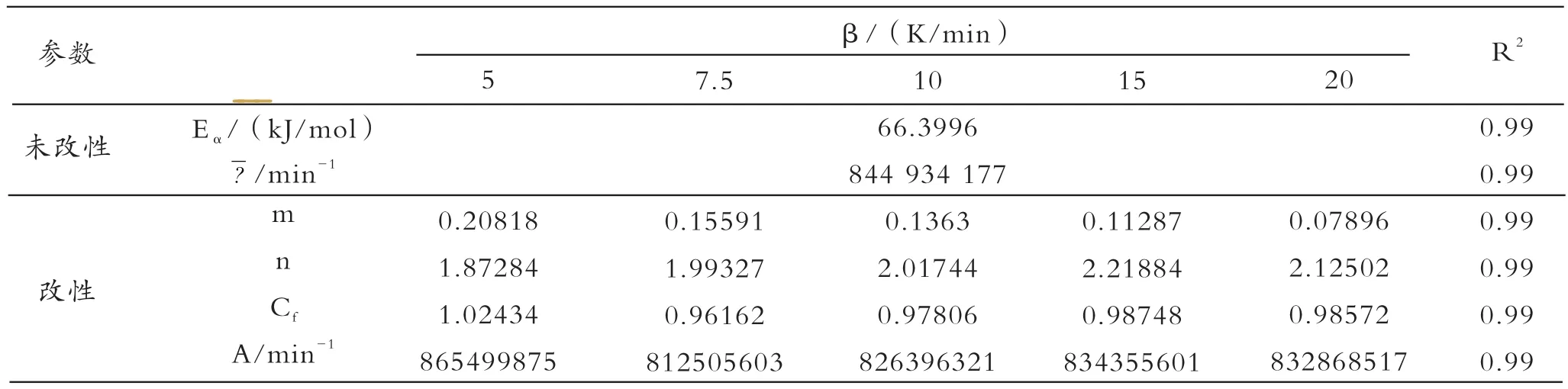
表2 自催化模型得到的动力学参数Tab.2 Kinetic parameters obtained from autocatalytic dynamic model

2.4 NLV Vyazovkin法

图3 a为10 K/min下固化度对温度的实验、拟合及修正拟合关系比较图，b为不同升温速率下实验、拟合及修正拟合的固化速率与温度之间的关系比较图Fig.3 a.Curing degree versus temperature:Comparison of experimental result and results of autocatalytic models with and without modified pre-exponential factor at 10℃/min，b.Curing rate versus temperature: Comparison of experimental results and resulta of autocatalytic models with and without modified pre-exponential factor at five heating rates

非模型法的基本假设为固化度相同，固化 速 率 仅 仅 是 温 度 的 函 数[10，16]， 将β=dT/dt代入方程（2），2边取自然对数并做关于T-1的微分可以得到方程（14）。

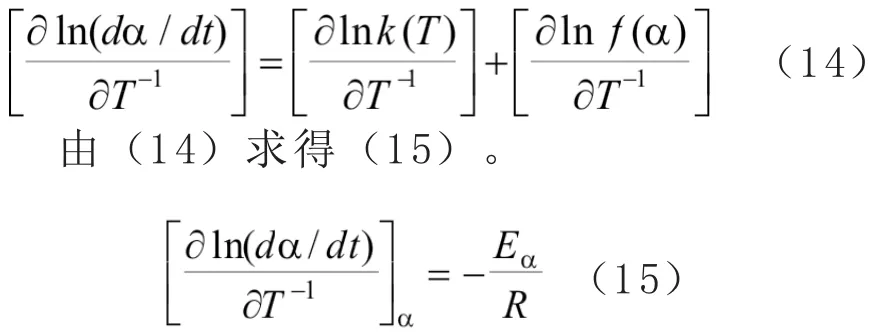
根据方程（15）可以得到给定固化度值相应的活化能Eα，等转化率原则已经广泛用于 Flynn、 Wall及 Ozawa等 积 分 法 中 ，Vyazovkin[17]考虑时间积分误差会影响E的

α变化，提出了方程（16）。

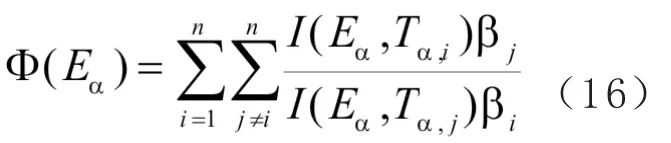
其 中Tα,i和 Tα,j为 不 同 实 验 达 到 给 定 固 化度时的温度，I为微小区间[αt， αt+△t]的积分值，对于恒定升温速率程序，其一般可以表示为近似方程（17）[5]。

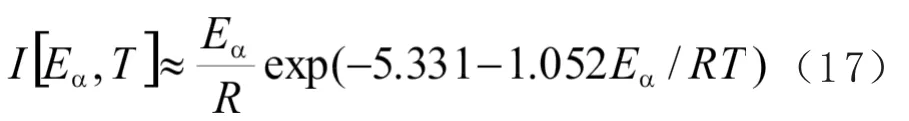
根据等转化率法的定义，升温程序对反应模型不造成影响，当给定了α值后在不同的5个β条件下的实验应当满足等式（18）。

那么由理论上可知，当n=5时，方程（16）右边能够计算得到确定值，但由于Tα的测定会出现误差，方程（18）的左边必定会有一个相对最小值。将实验得到的Tα和β代入方程（19），且随机改变Eα值，就能得到每一个给定的α对应的活化能Eα。实验计算α的取值范围为0.05～0.95，步长选择0.01，实验结果如图4所示。

由图4的活化能计算结果可以看出，反应体系前期自催化效应明显，活化能逐渐降低，反应后期随着反应位阻增大，分子链段运动所需要的能量增加，反应活化能又有所增加。

2.5 补偿参数法

补偿参数法认为，在固化过程中，活化能和指前因子会随着固化度、温度的变化而变化[16]。这种变化关系可以通过方程（20）来描述。

其中a，b为补偿参数，不同的实验会对应 不 同 的Ai和 Eαi。 为 了 尽 可 能 提 高DSC微 分 数据计算结果的精度，Sbirrazzuoli[18]认为，可以使用Achar-Brindley-Sharp-Wendworth（ABS）微分法来计算补偿参数。通过几组简化的SB方程特定指数m、n（分别是m=0，n=2；m=1，n=2；m=1，n=1；m=0.5，n=1.5；m=2，n=1），选择α范围在0.2～0.8之间，使用ln[dα/（f（α）dT）]对1/T作图，经线性拟合并根据截距求出ln（Ai） ，根据斜率求出Eαi， 计 算 结 果 列 于 表3中 。 得 到ln（Ai） 、Eαi后 ，再经线性拟合就可以得到不同升温速率条件下的补偿参数a，b值，具体值列于表4中，从而可以建立了不同升温速率条件下的ln（A）与Eα之间的关系。

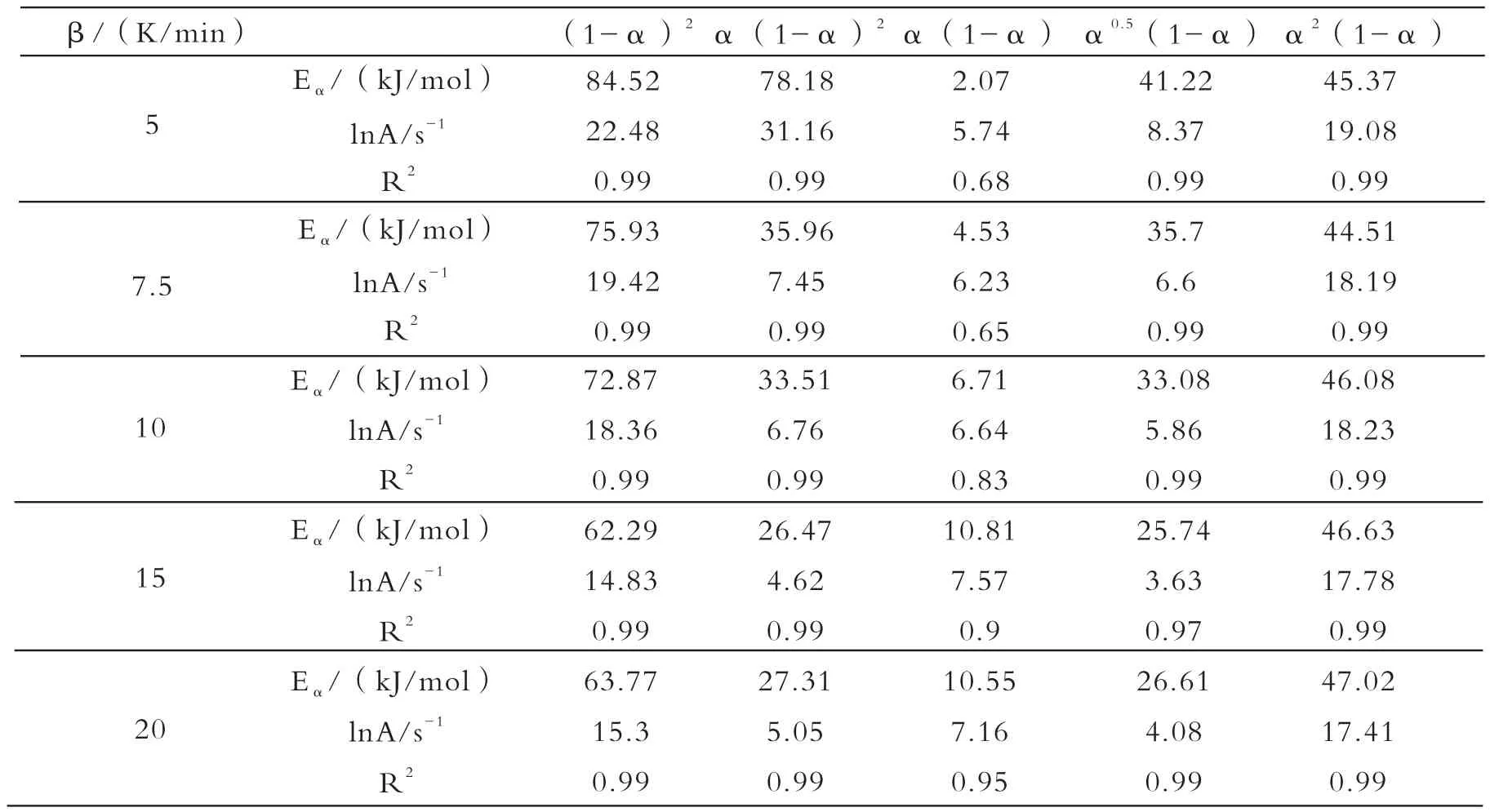
表3 使用ABS微分法计算得到的动力学参数Tab.3 Kinetic parameters obtained from ABS differential method

3 结论

（1）使用唯像模型法和非模型法对芳香胺/环氧树脂固化行为进行研究，提出了适合该体系的动力学模型及数学分析方法。

（2）唯像模型法中，引入了动力学修正因子Cf，对SB双参数模型进行修正拟合，修正后的拟合结果优于修正前，且更加逼近实验数据；非模型法中，通过NLV Vyazovkin法计算出不同α所对应的Eα值及反映固化过程中活化能Eα随固化度α的变化关系，从而证实了模型法中关于固化过程的描述。同时，补偿参数法中使用ABS微分法能相对精确地建立动力学因子之间的函数关系。

（3）本研究采用多重数学分析手段精确计算了动力学参数和拟合动力学过程，从方法论的角度为环氧树脂固化动力学的研究提供了理论依据。

表4 使用ABS微分法计算的补偿参数Tab.4 Compensation parameters obtained from ABS differential method

[1]肖婉萍,周德文,吕满庚,等.纳米填料对含长链取代基液晶环氧树脂固化动力学及热性能的影响[J].复合材料学报,2012,29(1):1-7.

[2]张靠民,顾轶卓,李敏,等.快速固化环氧树脂及其碳纤维/环氧复合材料性能[J].复合材料学报,2013,30(6):21-27.

[3]甘丽,孙志杰,顾轶卓,等.升温与等温法模型动力学研究环氧树脂固化反应[J].高分子学报,2010,54(8):1016-1022.

[4]张竞,黄培.环氧树脂固化动力学研究进展[J].材料导报,2009,23(13):58-61,81.

[5]Xia L J,Zuo L,Zha S W,et al.Kinetic research on low-temperature cure of epoxy adhesive[J].International Journal of Adhesion and Adhesives,2014,50(4):255-264.

[6]America Society for Testing and Materials.ASTM E2041-03 Standard Test Method for Estimating Kinetic Parameters by Differential Scanning Calorimeter Using the Borchardt and Daniels Method[S].West Conshohocken,America:American Society for Testing and Materials,2003.

[7]America Society for Testing and Materials.ASTM E2602-09 Standard Test Method for the Assignment of the Glass Transition Temperature by Modulated Temperature Differential Scanning Calorimetry[S].West Conshohocken,America:American Society for Testing and Materials,2009.

[8]Vyazovkin S.Evaluation of activation energy of thermally stimulated solid-state reactions under arbitrary variation of temperature[J].Journal of computational chemistry,1997,18(3):393-402.

[9]Yousefi A,Lafleur P G,Gauvin R.Kinetic studies of thermoset cure reactions:a review[J].Polymer Composites,1997,18(2):157-168.

[10]Vyazovkin S,Burnham A K,Criado J M,et al.ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data[J].Thermochimica Acta,2011,520(1):1-19.

[11]Má lek J.The kinetic analysis of nonisothermal data[J].Thermochimica acta,1992,200(92):257-269.

[12]Montserrat S,Málek J.A kinetic analysis of the curing reaction of an epoxy resin[J].Thermochimica acta,1993,228:47-60.

[13]Senum G I,Yang R T.Rational approximations of the integral of the Arrhenius function[J].Journal of thermal analysis,1977,11(3):445-447.[14]Šesták J,Berggren G.Study of the kinetics of the mechanism of solid-state reactions at increasing temperatures[J].Thermochimica Acta,1971,3(1):1-12.

[15]Sun L,Pang S S,Sterling A M,et al.Thermal analysis of curing process of epoxy prepreg[J].Journal of applied polymer science,2002,83(5):1074-1083.

[16]Moussa O,Vassilopoulos A P,de Castro J,et al.Early-age tensile properties of structural epoxy adhesives subjected to low-temperature curing[J].International Journal of Adhesion and Adhesives,2012,35(7):9-16.

[17]Vyazovkin S,Dollimore D.Linear and nonlinear procedures in isoconversional computations of the activation energy of nonisothermal reactions in solids[J].Journal of chemical information and computer sciences,1996,36(1):42-45.

[18]Sbirrazzuoli N.Determination of pre-Exponential factors and of the mathematical Functions f(α) or G(α) that describe the Reaction mechanism in a model-free way[J].Thermochimica Acta,2013,564(5):59-69.

Non-isothermal DSC kinetics of curing of epoxy resin with aromatic amine

ZHANG Si-si, ZHOU Ming-xuan, LI Wen-xiang, WU Pan-luo, GUAN Rong
(College of Chemistry and Chemical Engineering, Hubei University, Wuhan, Hubei 430062, China)

Based on the data obtained by the non-isothermal DSC tests, the reaction kinetics of curing of bisphenol-A epoxy resin with aromatic amine were investigated by using the phenomenological model method and the model-free method. In the phenomenological model method, we forecasted the curing system according with the SB double parameter autocatalytic model by employing the Málek method. To reduce fitting errors, the dynamic modification factor Cfwas introduced to revise the fitting obtained by using the least square fitting based on Levenberg-Marquardt (LM) algorithm. For the model-free method, using the improved isoconversional method (NLV method) the values of activation energy (Eα) at different curing degree(α) were obtained, and the compensation parameters were obtained through the ABS differential method for several simplified SB equations. The results show that by introducing the modification factor Cf, the SB double parameters autocatalytic model can better fit the kinetic process of curing reaction of the curing system. At the early stage of reaction, the Eαvalue falls off fast as α increased. But at the later period of reaction , the Eαvalue was gradually increased.In addition, the relationship between activation energy (Eα) and pre-exponential factor (A) can be expressed by the compensation parameter equation better.

epoxy resin; curing kinetics; modified model method; improved isoconversional method; compensation parameter method

TQ433.4+37

A

1001-5922（2017）11-0017-07

2017-05-13

张思思（1993-）女，硕士，研究方向为环氧树脂胶粘剂的改性。E-mail：1160758730@qq.com。

管蓉（1956-），女，博士，教授，博士生导师，研究方向为高分子材料的结构与性能、胶粘剂、高分子电解质膜等。E-mail：rongguan@hubu.edu.cn。