理想格上基于身份的代理重签名方案

商玉芳，梁向前，孙意如

山东科技大学 数学与系统科学学院，山东 青岛 266590

理想格上基于身份的代理重签名方案

商玉芳，梁向前，孙意如

山东科技大学 数学与系统科学学院，山东 青岛 266590

代理重签名作为密钥管理的一个重要工具，它不仅能够简化密钥管理、简化证书管理，还能够提供路径证明等功能。目前，针对基于大整数分解与离散对数的困难问题，在量子环境下代理重签名方案的不安全性，有人提出了一种能够抵抗量子攻击的代理重签名。利用理想格，以及基于理想格上的小整数解的困难性，构造了理想格上基于身份的代理重签名方案，该方案与其他的具有相同性质的基于身份的代理重签名方案相比，具有较短的签名和公钥、运算复杂度降低的优点。

代理重签名；理想格；小整数解问题

1 引言

代理重签名的概念最早于1998年在欧密会上由Blaze，Bleumer等人[1]提出。在代理重签名方案中，Alice和Bob之间存在着一个半可信的代理者，作为他们两者之间的转换者，即代理者能够把一个消息m在Alice下的签名转换为Bob在同一消息m上的签名，同时，代理者拥有一个重签名秘钥，并且由Alice和Bob的私钥生成，但是，代理者不能代理Alice或Bob在任一消息上进行签名，因为代理重签名相当于一个变换函数，它具有很多的应用场景，如简化秘钥管理、提供路径证明、透明认证等。

自 2005 年以来，Ateniese[2]，Libert[3]，Schnorr[4]，Shao[5]等人对文献[1]方案进行了深入分析之后，分别给出了代理重签名的新的形式化定义和安全模型，在标准模型下可证明安全的代理重签名方案，以及构造了第一个基于身份的单项代理重签名方案等。近几年来随着量子计算机的出现，对于传统一些基于有限域上的困难假设的密码学方案，证实了他们不能够有效地抵抗量子计算机的攻击，由于格密码是一类抗量子计算机的密码体制，因此，在格上构造签名方案成为一个新的研究热门方向。2010年，Ruckert等人[6]在随机预言机模型和标准模型下分别构造了基于格困难问题的基于身份的方案，2012年，Daniele Micciancio和Chris Peikert[7]提出了新的格陷门生成算法，而且提出了一个基于格的强不可伪造的签名方案。2014年，Ducas等人[8]根据文献[9]提出了格陷门生成算法，利用理想格，提出了一个相对较短的签名方案。2015年杨丹婷等人[10]提出了一个理想格上基于身份的签名方案。

本文利用文献[7]理想格上特殊的代数结构，构造了具有不可伪造性的基于身份的代理重签名方案，该方案的安全性是基于小整数解的困难问题，与其他基于身份的签名方案相比，具有强不可伪造性、相对较短的公钥和签名长度。

2 预备知识

2.1 格

定义1[11]格是Rm中一类具有周期性结构离散点的集合。严格的说格是m维欧式空间Rm的n(m＞n)个线性无关的向量组b1,b2,…,bn∈Rn的所有整系数的线性组合，即

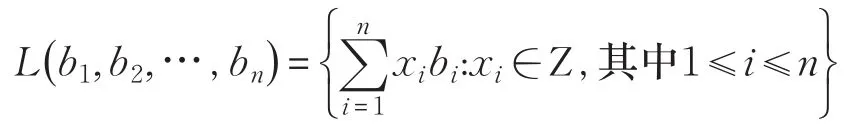
这里b1,b2,…,bn∈Rn构成了格Λ的一组基。

注：同一个格可以用不同的格基来表示，在上面的定义中，m为格的维数，n为格的秩，若满足m=n，则称为满秩格。该文主要关注的是整数格，即Λ∈Zm。

定义2[11]设q是一个素数，A∈Zqn×m，u∈Zqn，两个整数格 Λ⊥q(A )和 Λuq(A)分别定义为：

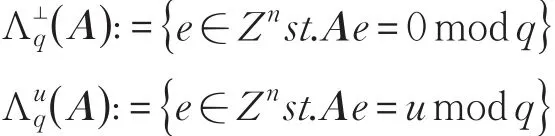
有定义知Λuq(A )=Λ⊥q(A )+s，其中 s∈Λuq(A)。

2.2 理想格

定义3[7]环Zn的理想I又是格Zn的子格，称这个子格为格Zn的理想格。具体定义如下：多项式环若满足以下三条性质：

（1）f(x)的首项（最高次的项）系数为1。

（2）在Z上是不可约的。

（3）对环 Z[x]上的任意多项式 f(x)和g(x )，都有

||g(x)h(x)modf(x)||＜ poly(n)||g(n)||⋅||f(x)||成立，则称环的理想为 f()x-理想格，有时也简写为I。

本文所考虑的格问题都局限于理想格，而且所研究的结论适应于任意分圆环的理想格，所使用环的形式为ℜ=Z[x]/(Φ2n(x))或 ℜq=(ℜ/qℜ)，其中 q=3k∈Z ，n是2的幂次方，Φ2n=Xn+1是分圆多项式。

2.3 格上的困难问题及离散高斯分布

定义4[12]（SISq,n,m,β小整数解问题）给定一个矩阵A∈Zn×mq，q为整数，β为大于零的实数，求解一个非零向量v，满足 Av=0modq且||v||≤β，其中v∈Λ⊥q()A。

定义5[9]（RingSISq,n,m,β环上小整数解问题）给定行向量 A∈ℜl×mq、q为整数、β为大于零的实数，求解一个非零向量v，使得v∈Λ⊥q()A ，并且满足||v||≤β。

定义6[13]（高斯函数）对任意的n维格Λ、向量c∈Rn和实数s＞0，定义Rn上的高斯函数为：

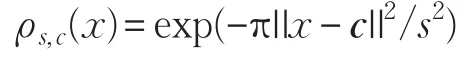
其中，对任意的x∈Rn，c为中心，s为标准差。如果下标c，s为0时，可省略不写。

定义7[13]（高斯分布）格Λ上的离散高斯分布为：对任意的n维格Λ、向量c∈Rn和实数s＞0，有

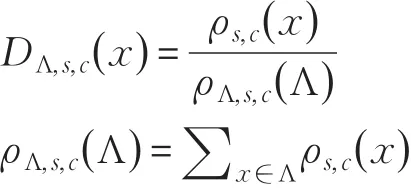
同高斯函数的定义下标s，c也可省略不写。

定义8[12]（格陷门）设A∈Zn×mq，G∈Zn×wq，可逆矩阵 H∈，其中，m＞w＞n，若满足则称R∈为A的一个G-陷门。

2.4 相关定理

定理1[14]存在一个概率多项式时间算法TrapGen(q,n)，设 q≥3是一个奇数，且 m=6nlbq，则输出两个矩阵 A∈和T∈，A在上是接近于均匀的，T是格Λ⊥q(A)的一组基，除了一个可忽略的概率外，且和 ||T||≤Ο((nlbq))同时成立，其中，‖‖⋅表示为欧几里德范数。

定理2[8]设q≥2，矩阵 A∈Zn×mq，m＞n，T 是格ΛΛq(A)的一组基，，那么对于c∈Rm,u∈Znq有：

（2）存在一个概率多项式时间算法Samplepre(A,T,u,σ)，抽取一个Λuq(A)中的向量 x，使得 x的分布统计接近于 DΛuq(A),σ,c。

定理3[11]存在一个有效的多项式算法SampleD(A,u,R,s)，输入矩阵 A∈，u∈ℜq，可逆标记H∈ℜ对应 A的一个G-陷门R∈和参数s1(R )，输出一个与分布统计上相近的抽样。

定理4[11]设，且，则s1()R ≤s⋅以压倒性优势的概率成立。

定理5[10]存在一个陷门委托算法DelTrap(A′=[A |A1],H ′,s′)，输入矩阵逆矩阵，参数 s′≥η(Λ)，其中 Λ=Λ⊥(A)，输出矩阵 A′的陷门

定理 6[12]设是 [A ,A]的G-陷门，

i，标记 Hi∈ℜq，则对ci∈ℜq，任意的线性组合的G-陷门，其中标记

定理7[12]（最小熵）设，以极大的概率选择 A，且A←Uw，若从 Dℜ,s中独立随机选取 xi(i=1,2,…,w)，则对任意的非零向量v∈ℜw{0} 的最小熵为，所以的概率是小于Ω(n)的。

定理8[12]（左基取样）存在一个多项式时间算法SampleBasisLeft(A,M,TA,0,σ)，输入矩阵 A、M ，M∈，格 Λ⊥q(A)的一组短基TA，输出格的 一 组 短 基 TF1，其 中 F2=A|M ，

3 基于身份的代理重签名的一般模型

基于身份的代理重签名一般模型由以下多项算法KeyGen，Extract，Rekey，Sign，Resign，Verify组成：

（1）KeyGen(1n)：输入一个安全参数n，输出该方案的公共参数 pp和主密钥msk。

（2）Extract(pp,msk,id)：输入一个安全参数 pp，主密钥msk和用户身份id，运用私钥提取算法输出id的私钥。

（3）Rekey(p kA,skB)：输入用户A的公钥的 pkA，用户B的私钥skB，运用重签名密钥生成算法，输出用户A和B之间的重签名秘钥rkA→B。

（4）Sign(p p,skid,m ) ：输入安全参数 pp，私钥skid以及消息m，运用签名算法输出消息m的签名σ。

（5）Resign(r kA→B,pkA,m,σ) ：输 入 重 签 名 密 钥rkA→B，消息m，用户A的公钥 pkA以及用 pkA来验证m的签名σ，运用重签名算法输出消息m的签名σ′。

（6）Verify(p p,pkB,m,σ′)：输入安全参数 pp，用户B的公钥 pkB，消息m以及重签名σ′，验证重签名算法是否是合法签名，如果是则接受，否则拒绝。

4 方案介绍

（1）KeyGen(1n)：输入安全参数n，算法如下：

② 随机选择向量Ai,Bj(0 ≤i≤1),(0 ≤j≤d )，l为用户身份的长度，d为消息的长度，以及

③ 输出pp=(A0,A1,…,Al,B1,B2,…,Bd,U,v )公共参数及主密钥Msk=T。

（2）Extract( )pp,Msk,id ：输入公共参数 pp，用户身份id及主密钥T。

（3）Rekey(FidA,FidB,rkA→B)：输入用户 A的公钥FidA，用户B的公钥FidB及私钥RidB。

①设用户FidA=( )a11,a12,…,a1n

T，对任意的b1i∈ℜq，i=1,2,…,n 。

②根据定理2，运行原像抽样算法Samplepre(FidB,RidB,a1i,σ)，抽取向量 δi，使得 FidBδi=a1imodq 且||δi||≤，令SidA-idB=( )δ1,δ2,…,δm，FidBSidA-idB=Fmodq，且满足输出重签名密钥 rkidA→idB=

（4）Sign(p p,skid,m )：输入公共参数 pp，私钥skid，消息m∈(0 ,1)nk∈ℜkq。

①随机选取向量r∈{0 ,1}nk和标记T，计算：

以及u=Uu+v∈ℜq，其中参数U∈ℜl×kq,v∈ℜq。

② 由定理3，运行 SampleD( )Fid,u,R,s算法，，输出一个与DΛ⊥u(Ai)⋅s分布统计上相近的抽样，输出用户A对消息m的签名σ=(i dA,eidA,t)。

（5）Resign(r kA→B,FidA,m,σ) ：输 入 重 签 名 密 钥rkA→B=SidA-idB，用户A及其公钥FidA，消息m和用户A对消息m签名σ=(i dA,eidA,t)。

①代理者首先验证用户A对消息m签名的正确性，即 FidAeidA=umodq 且是否同时成立。

②若上式成立，则利用代理重签名密钥计算重签名eidB=SidA-idBeidA，即输出用户 A→B的重签名为σ′=(i dB,eidB,t)。

（6）Verify(p p,FidB,m,t)：输入公共参数 pp，用户B的公钥FidB，消息m和用户 A→B对应的重签名σ′=(i dB,eidB,t)。

利用计算出的Fid,Ft及t，验证如果满足同时成立，则接受重签名σ′，否则拒绝。

5 方案的安全性分析

定理9在随机预言机模型下，本文基于身份的代理重签名方案是在环上的小整数解问题(R ingSISq.n.m.β)的困难假设下的，其中，假设存在一个概率多项式时间敌手A在进行了至多M 次的询问，ε≥2-Ο(n)，且 1≤M≤2Ο(n)，当 敌 手 A进 行S次 询 问 时 ，S∈{ }

0,1,…,M-1，在运行时间T内，以概率ε攻破该方案，构造了一个算法 B，则利用敌手 A以概率来解决RingSISq.n.m.β困难问题。

证明 以下证明过程包括6部分（证明过程可部分参考文献[12]和文献[13]）。

（1）参数生成：敌手A将(i d ′,m(1),m(2),…,m(p))发送给模拟者 B，id′为目标身份且id′=(b ′1,b′2,…,b′l) ∈(0 ,1)l，m(1),m(2),…,m(p)为 p个选择的消息。

（2）私钥提取询问：当敌手A询问用户身份id的私钥时，且 id≠id′，模拟 B将计算用户公钥 Fid=，通过运行左基取样算法，R←将产生的私钥R发送给敌手A。

（3）重签名密钥询问：当敌手A对身份(i dA,idB)进行重签名密钥询问时，若idA=idB时，询问停止，否则，模拟者B计算重签名密钥rkidA→B，首先利用用户A的公钥FidA和用户B的公私钥对(FidB,RidB)，以及重签名密钥生成算法生成的重签名密钥rkidA→idB=SidA-idB，使得AidBSidA-idB=AidAmodq并发送SidA-idB给敌手A。

（4）签名询问：模拟者 B 首先根据 id′=(b′1,b′2,…,b′l)目标身份产生公开参数 A0,A1,…,Al,i=0,1,…,l，令 Ai=EiG-A0Ri，Ri为 [A0,Ai]的一个G-陷门 且Ri∈ ℜlq×

w因为g为一个环同态[7]，Ei表示为：

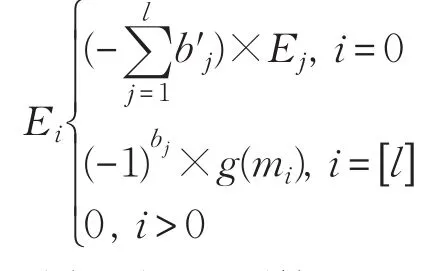
分析可得以下结论:

①当id=id′时：

②当id≠id′时：

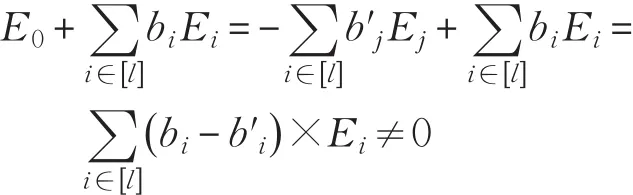
同样令 A′=E′iG-A0R′i，R′i为 [A0,A′i] 的一个G-陷门且 R′i∈ ℜlq×w。再根据消息m(1),m(2),…,m(p)生成公开参数B0,B1,…,Bd（下面计算过程可参考文献[51]）当模拟者B计算串q∈{0 ,1}≤d的集合Q时，d为消息m(i)，i∈{0 ,1,…,p}的长度，且有|Q|=(d -1) p+1，q不是任意消息m(i)的前缀，则选择任意的q∈Q且记γ=|q|≤d ，其中 E′i表示如下：

通过分析得出结论：

①对任意消息m不以q为γ位前缀时，而是以φ为γ位前缀时：

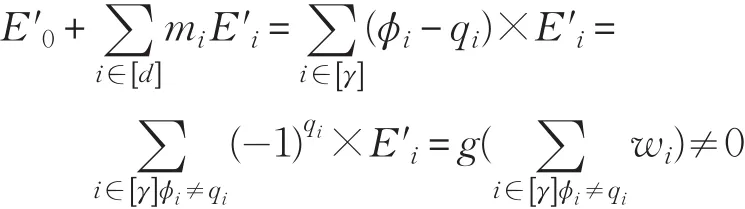
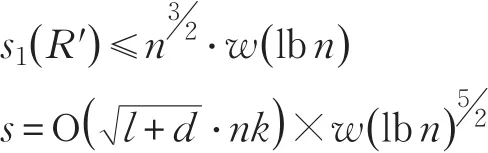
所以利用多项式算法SampleD产生id′在消息m上的签名，最后将签名发送给敌手A。

（5）重签名询问：当敌手A询问用户身份id(i d ≠id′)在消息m上的重签名，模拟者B首先对消息m上的签名σ进行验证。若Verify( )pk,m,σ=1成立，则利用重签名密钥计算出重签名σ′，并发送σ′给敌手A。

（6）伪造阶段：敌手A对消息m′进行伪造签名，对每个消息m(j)，当模拟者B随机选取t(j)∈T，如果前缀发生碰撞，有且j≠s，则模拟者发生的概率至多为否则，当模拟者B随机选择一个前缀B希望有t≤∗γ=t′≤γ，敌手输出伪造签名 σ′=(id′,e′,t′)，由于敌手认为t≤∗γ∈Tγ是独立选取的，故t≤∗γ=t′≤γ发生的概率为1|Tγ|。故若不是，则中止模拟。

设 v=Ft′e′-U ⋅u′,则有Ft′e′=U ⋅u′+v。

令 Ft∗⋅e∗=U⋅u∗+v 对任意的，当时F=[A |-AR|E′G-AR′]，有 E=E=0t00id′t0t∗t′以及 RU←Dℜ,σ′,U=A0Ru则有：

由以上分析可得A0φ=0，下面令：

可知ψ≠0且很小（根据文献[8]可知）ψ=0的概率是小于 2-Ω(n)，由于 σ∗，σ′是有效的签名且 ||σ∗||,||σ′||≤，此外，对于任意的标记，所以可得到

6 效率分析

本文提出的基于身份的代理重签名方案，较好地利用了理想格所特有的结构，使其具有较高的运算效率，减少了运算的复杂度，所以该方案要比其他同类的基于身份的方案的运算速度快得多。在本方案中，使用了Hash函数运算，以及陷门委托算法、原像抽样算法，下面是将本文方案与基于相同性质的文献的方案进行比较，分析结果如表1。

表1 方案的效率对比

7 结论

本文利用理想格，构造了一个新的在标准模型下给出安全性证明的基于身份的代理重签名方案，该方案的安全性基于环上的小整数解困难问题，即在RingSIS假设下，该方案满足不可伪造性，与其他的基于身份的签名方案相比，充分地利用了理想格中的特殊的代数结构，构造的签名方案具有较短的签名和相对较短的私钥长度，降低了运算复杂度，提高了运算效率。

[1]Blaze M，Bleumer G，Strauss M.Divertible protocols and atomic proxy cryptography[J].Lecture Notes in Computer Science（LNCS），1998，1403：127-144.

[2]Ateniese G，Hohenberger S.Proxy re-signatures：new definitions，algorithms，and applications[C]//ACM Conference on Computer and Communications Security，Alexandria，VA，USA，2005：310-319.

[3]Libert B，Vergnaud D.Multi-use unidirectional proxy resignatures[C]//ACM Conferenceon Computerand Communications Security，Alexandria Virginia，USA，2008：511-520.

[4]Schnorr C P.Efficient identification and signatures for smartcards[J].Lecture Notes in ComputerScience（LNCS），1990，435：688-689.

[5]Shao Jun，Feng Min，Zhu Bin，et al.The security model of unidirectional proxy re-signature with private re-signature key[J].Lecture Notes in Computer Science（LNCS），2010，6168：216-232.

[6]Rückert M.Strongly unforgeable signatures and hierarchical identity-based signatures from lattices without random oracles[C]//Post-Quantum Cryptography.Berlin Heidelberg：Springer，2010：182-200.

[7]Micciancio D，Peikert C.Trapdoors for lattices：Simpler，tighter，faster，smaller[C]//Advances in Cryptology—EUROCRYPT 2012.Berlin Heidelberg：Springer，2012：700-718.

[8]Ducas L，Micciancio D.Improved short lattice signatures in the standard model[C]//Advances In Cryptology-CRYPTO 2014.Berlin HeidelbErg：Springer，2014：335-352.

[9]赛炜，胡予濮.基于理想格的公钥密码中模多项式的应用研究[D].西安：西安电子科技大学，2014，1：10-11.

[10]Yang D T，Xu C G，Xu L，et al.Identity-base signature scheme over ideal lattices[J].Journal of Cryptologic Research，2015，2（4）：306-316.

[11]Alwen J，Peiker C.Generating shorter bases for hardrandom lattices[C]//The 26th International Symposium on Theoretical Aspects of Computer Science，Freiburg，Germany，2009：535-553.

[12]Gentry C，Peikert C，Vaikuntanathan V.Trapdoors for hard lattices and new cryptographic constructions[C]//Symposium on Theory of Computing 2008，Victoria，British Columbia，Canada，2008：197-206.

[13]李明祥，刘阳，赵秀明.高效格上的基于身份的签名方案[J].计算机应用研究，2014，3（3）：825-828.

[14] 王小云，刘明洁.格密码学研究[J].密码学报，2014，1（1）：13-27.

[15]Cash D，Hofheinz D，Kiltz E，et al.Bonsai tree，or how to delegate a lattice basis[C]//Proceedings of the 29th Annual International Conference on Theory and Applications of Cryptographic Techniques，2010：523-552.

SHANG Yufang,LIANG Xiangqian,SUN Yiru

College of Mathematics and Systems,Shandong University of Science and Technology,Qingdao,Shandong 266590,China

Identity-based proxy re-signature over ideal lattice.Computer Engineering and Applications,2017,53（21）：110-114.

As an important tool of key management,the proxy re-signature scheme can not only simplify the secret key management and certificate management,but also can be used to provide certificate path and so on.Currently,for the difficulty of integer factorizating and logarithm discretization and the insecurity of proxy re-signature schemes in the quantum environments,a proxy re-signature scheme that can resist the attack of quantum has been presented in the literature.The first identity-based proxy re-signature scheme over ideal lattice is constructed in this paper,by using ideal lattice and based on the difficulty of the Small Integer Solution（SIS）problem.Compared with other proxy re-signature scheme that has the same properties,this has a shorter signature,and public key,and the advantage of decreasing the computational complexity.

proxy re-signature;ideal lattice;Small Integer Solution（SIS）problem

A

TN91

10.3778/j.issn.1002-8331.1605-0428

国家自然科学基金（No.61402265，No.61170054）。

商玉芳（1990—），女，硕士研究生，主要研究领域为信息安全理论与应用；梁向前（1969—），男，博士，副教授，主要研究领域为信息安全，E-mail：liangxq87@126.com；孙意如（1991—），女，硕士研究生，主要研究领域为信息安全理论与应用。

2016-05-31

2016-07-05

1002-8331（2017）21-0110-05

CNKI网络优先出版：2016-11-21,http://www.cnki.net/kcms/detail/11.2127.TP.20161121.2047.064.html