基于分数阶傅里叶变换的LFM信号参数估计

渠莹+杨俊

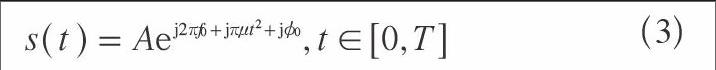
摘 要：线性调频信号作为一种典型的非平稳信号，具有大时宽带宽积的特殊优势，广泛应用于雷达、通信、地质探测和声呐信号处理等研究领域。因此，研究线性调频信号具有十分重要的意义。分数阶傅里叶变换实质上是一种线性变换，它不仅可以理解为chirp基分解，还没有交叉干扰的问题。所以，分数阶傅里叶变换特别适合用来处理chirp类信号。文中基于分数阶傅里叶变换，研究了线性调频信号的检测和参数估计算法。首先利用Matlab对线性调频信号进行仿真，并分析了其时域波形特性；然后在不同信噪比的背景下，对单分量和多分量的线性调频信号进行了参数估计。仿真结果表明：在噪声环境中，分数阶傅里叶变换能够检测出线性调频信号的相关参数，设计的线性调频信号参数检测估计仿真软件具有较好的交互性能。

关键词：线性调频信号；分数阶傅里叶变换；信号检测；参数估计

中图分类号：TP39；TN953 文献标识码：A 文章编号：2095-1302（2017）11-00-03

0 引 言

线性调频（chirp）信号作为最常见的调频信号，具有大时宽带宽积的优势，广泛应用于雷达信号处理、医学成像处理、地质探测、声纳信号处理等领域，因此，该信号的检测与估计具有重要意义[1，2]。Wigner-Ville分布方法在对线性调频信号进行检测时，会有交叉项干扰[2，3]；短时傅里叶变换对线性调频信号检测时，虽然具有较快的速度，但估计精度有待进一步提高[4]；小波变换能够较好地完成线性调频信号的时频分析，但实时性能较差[5]。

本文实现了基于分数阶傅里叶变换的线性调频信号检测与估计。仿真结果验证了算法的有效性和可靠性。

1 分数阶傅里叶变换的线性积分定义

定义在时间域的函数 x（t），其p阶分数阶傅里叶变换（FRFT）[6，7]是一种线性积分运算，表示如下：

公式（2）给出了FRFT的线性积分定义，但其不具备移不变性。因为核函数Kp（u，t）与时间t和阶次p都有关系。这里我们分析特殊阶次的FRFT：

（1）当p=4n，即α=2nπ时，函数x（t）的FRFT等于函数本身，即F4n为恒等算子I。

（2）当p=4n±2，即α=（2n±1）π时，函数x（t）的FRFT等于x（-t），即F4n±2为奇偶算子P。

（3）当p=1，即α=π/2时，函数x（t）的FRFT等于函数的FT，即F1退变为FT算子F。

（4）当p=-1，即α=-（π/2）时，函数x（t）的FRFT等于函数的傅里叶逆变换F-1。

从情况（3）可知，X1（u）就是x（t）的普通傅里葉变换。同理，我们从上面可以得到函数x（t）的傅里叶逆变换，即X-1（u）。

2 基于分数阶傅里叶变换的线性调频信号检测

在分数阶傅里叶域的线性调频信号有一个优点，即线性调频信号的能量聚集性会随着阶数的不同而改变。根据该特点，就可对含有未知参数的线性调频信号进行检测。把旋转角α当作检测时所用的变量，然后再对观测信号作分数阶傅里叶变换，把线性调频信号的能量分布在二维平面（α，u）上，最后按照事先设置好的阈值对信号峰值点的位置进行检测，即可实现线性调频信号的检测和参数估计。

线性调频信号的频率会随着时间的不断变化而变化，且两者间是线性关系。可以通过数学表达式给基本的线性调频信号建立如下模型：

其中，A，φ0，f0和μ分别表示线性调频信号的幅度，初始相位，起始频率和调频斜率，T表示线性调频信号的持续时间。

在本模型中，线性调频信号的持续时间和观测时间都为[0，T]。这里假设线性调频信号的终止频率为fm，那么线性调频信号的调频斜率可以表示为μ=（fm-f0）/T。

将含有噪声的单分量线性调频信号表示为如下模型：

把旋转角α当作检测的变量时，分数阶傅里叶变换 （FRFT）可以在FFT的帮助下大大减小计算量。在处理多分量线性调频信号时，分数阶傅里叶变换和WVD变换相比，能够避免后者复杂的变换过程，且分数阶傅里叶变换作为一种线性变换，还可以排除交叉项的干扰。此外，分数阶傅里叶变换在对线性调频信号参数进行估计时，可以保留线性调频信号的相位信息。

3 算法仿真结果与分析

3.1 线性调频信号参数估计

设置线性调频信号的幅度为1，起始频率为20 Hz，采样频率为800 Hz，终止频率为100 Hz。线性调频信号的持续时间为2 s，那么信号的观测时间为[0 s， 2 s]。设置好这些参数后，单分量的线性调频信号仿真波形如图1所示。

还可以利用Matlab产生一个多分量的线性调频信号，信号1的幅度为1，起始频率为20 Hz，采样率为800 Hz，终止频率为100 Hz；信号2的幅度为1，起始频率为20 Hz，采样率为800 Hz，终止频率为200 Hz；信号3的幅度为1，起始频率为20 Hz，采样率为800 Hz，终止频率为400 Hz。它们的观测时间都设置为2 s。多分量线性调频信号的综合仿真波形如图2所示，参数估计结果如图3所示。从图中可以清楚地知道线性调频信号调频斜率的真实值（设计线性调频信号时所给出的调频斜率）和测量值以及它们之间的误差。

3.2 多分量信号的时频估计

多分量的线性调频信号为 X2（t），信号1的幅度为1，采样率为800 Hz，起始频率和终止频率分别为20 Hz、100 Hz，线性调频信号的观测时间为2 s；信号2的幅度为1，采样率为800 Hz，起始频率和终止频率分别为20 Hz、200 Hz，线性调频信号的观测时间为2 s；信号3的幅度为1，起始频率为20 Hz，采样率为800 Hz，终止频率为400 Hz，线性调频信号的观测时间为2 s。不含有噪声的多分量线性调频信号的仿真波形如图4所示，含有噪声的多分量线性调频信号的仿真波形如图5所示。endprint

从仿真结果可以看出，叠加在一起的多分量线性调频信号在不含噪声和含有噪声（6 dB）的情况下，信号变换杂乱无章，幅度不在[-1，1]区间。单从时域已经看不出信号的变化规律，因此我们需要借助时频分析来进一步分析。

多分量线性调频信号设置如下：

信号1的幅度为1，起始频率1 kHz，采样率为40 kHz，终止频率为10 kHz，线性调频信号的观测时间为0.2 s；

信号2的幅度为1，起始频率1 kHz，采样率为40 kHz， 终止频率为2 kHz，线性调频信号的观测时间为0.2 s；

信号3的幅度为1，起始频率1 kHz，采样率为40 kHz，终止频率为20 kHz，线性调频信号的观测时间为0.2 s。

在不含噪聲和含有噪声（3 dB）的情况下，线性调频信号的时频分析仿真结果如图6与图7所示。

从仿真结果可以看出，在没有噪声的环境中，多分量线性调频信号的短时傅里叶变换在时频平面上为三条具有不同斜率的直线，而且它没有受到噪声的污染，能量比较集中；在信噪比为3 dB的环境中，线性调频信号在时频平面上也为三条具有不同斜率的直线，能够较为清晰地检测到信号。

4 结 语

本文实现了基于分数阶傅里叶变换的线性调频信号检测，仿真结果表明，即使在噪声环境中，本文方法仍然可以对线性调频信号进行有效的检测与估计。

参考文献

[1]吴进，孔辉. 一种利用线性调频信号的新型扩频调制技术[J].电讯技术，2017，57（4）：397-401.

[2]李秀坤，吴玉双.多分量线性调频信号的Wigner-Ville分布交叉项去除[J].电子学报，2017，45（2）：315-320.

[3]张学俊，梁晨，糜玉林.基于WVD的LFM信号检测方法研究[J].物联网技术，2013，3（4）：29-32.

[4]迟华山，王红星，郭奇.短时傅里叶变换在线性调频信号时频滤波中的应用[J].电讯技术，2012，52（2）：155-159.

[5]郑生华，徐大专.基于小波脊线-Hough变换的LFM信号检测[J].量子电子学报， 2008，25（2）：145-150.

[6]杨玉婷，张廷蓉，龚霞.余弦高斯光束通过含球差分数傅里叶变换系统的传输[J].光学学报， 017（2）：77-83.

[7]李婧，沙学军，梅林，等.基于加权分数傅里叶变换域的2天线发射方法[J].哈尔滨工业大学学报， 2017，49（5）：10-15.

[8]李志明.一种基于Radon变换的文档图像倾斜校正改进算法[J].物联网技术，2016，6（7）：62-65.endprint