细说中考高频题

戴晓燕 樊翠霞

细说中考高频题

戴晓燕 樊翠霞

勾股定理及其逆定理在近几年的中考中是热点问题，以下就以2017年部分中考题为例，希望为大家带来一些思考和借鉴.

一、弦图的应用

例1（2017·长春）图1是我国汉代的赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”.此图案的示意图如图 2，其中四边形ABCD和四边形EFGH都是正方形，△ABF，△BCG，△CDH，△DAE是四个全等的直角三角形，若EF=2，DE=8，则AB的长为 .

图1

图2

【解】AF=DE=8，EF=2，AE=6，由勾股定理求得AD=10，故AB=AD=10.

例2（2017·石家庄一模）图甲是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的，若AC=6，BC=5，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到图乙所示的“数学风车”，则这个风车的外围周长是（ ）.

A.52 B.42 C.76 D.72

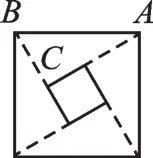
图甲

图乙

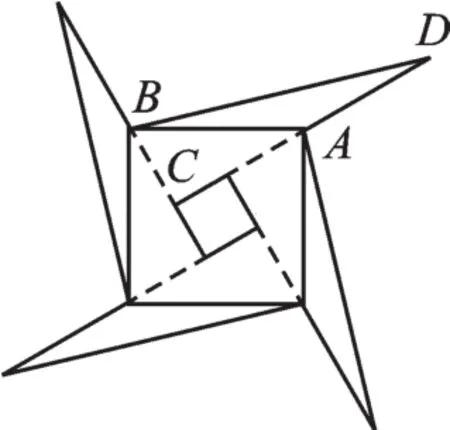
图3

【解】如图3，由AC=6，得DC=12，在直角△DBC中，由BC=5，DC=12得BD=13，所以BD+AD=19，故周长为19×4=76.

【评析】教材中应用“赵爽弦图”证明勾股定理，“赵爽弦图”是初中数学的重要基本图形之一，近年来在全国各地的中考题里常有出现.

二、折叠问题

例3 （2017·武威）如图4，一张三角形纸片ABC，∠C=90°，AC=8cm，BC=6cm.现将纸片折叠：使点A与点B重合，那么折痕长等于____cm.

图4

图5

【解】如图5，作AB的垂直平分线，分别交AB、AC于D、E，在Rt△BEC中，由勾股定理得（8-BE）2+62=BE2，解得，进一步算得

例4 （2017·嘉兴）一张矩形纸片ABCD，已知AB=3，AD=2，小明按下图步骤折叠纸片，则线段DG长为（ ）.

【解】由翻折得到△A′DE，△B′GE是等腰直角三角形

【评析】统观近年各省市的中考试题，不难发现“折叠”问题在中考试题里频频出现，而利用勾股定理建立方程是解决问题的重要方法.命题者通常以直角三角形为载体，以数形结合、方程思想等重要的数学思想为依托，实现了对“四基四能”的全面考查.

三、逆定理的应用

例5 （2017·益阳）如图6，△ABC 中，AC=5，BC=12，AB=13，CD是AB边上的中线，则CD=

.

图6

【解】由AC=5，BC=12，A B=13知△ABC是直角三角形，故CD=6.5.

例6（2017·南京）“直角”在初中几何学习中无处不在.如图7，已知∠AOB.请仿照小丽的方式，再用两种不同的方法判断∠AOB是否为直角（仅限用直尺和圆规）.

小丽的方法：如图8，在OA、OB上分别取点C，D，以C为圆心，CD长为半径画弧，交OB的反向延长线于点E.若OE=OD，则∠AOB=90°.

图7

图8

图9

图10

【解】方法1：如图9，在OA、OB上分别截取OC=4，OD=3.若 CD=5，则 ∠AOB=90°.方法 2：如图10，在OA，OB上分别取点C，D，以CD为直径画圆.若点O在圆上，则∠AOB=90°.

【评析】勾股定理的逆定理主要是由数量关系确定三角形是否为直角三角形，然后在直角三角形的背景下解决有关问题.勾股定理的逆定理体现了由数到形的重要数学思想，在近年来各地的中考题中常有出现，但往往考查定理本身，故难度不是太大.

四、旋转问题

例7 （2013·包头）如图11，点E是正方形ABCD内的一点，连接AE、BE、CE，将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1，BE=2，CE=3，则∠BE′C= 度.

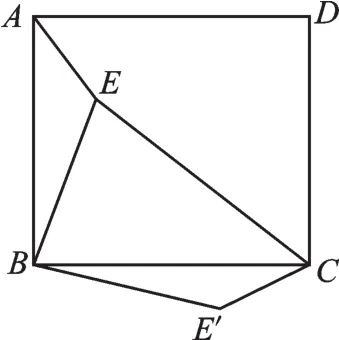
图11

图12

【解】本题采用分割的方式，如图12，通过连接EE′将∠BE′C转化为∠BE′E与∠EE′C的和.首先根据旋转的性质得∠EBE′=90°，BE=BE′=2，AE=E′C=1，那么，在Rt△EBE′中，由等腰直角三角形，可得∠BE′E=45°，由勾股定理可得此时△EE′C的三边长都已知了，且E′E2+E′C2=8+1=9，EC2=9，即 E′E2+E′C2=EC2，又由勾股定理的逆定理知△EE′C是直角三角形，所以可得∠EE′C=90°.故∠BE′C=135°.

【评析】根据已知得出△EE′B是等腰直角三角形比较容易，但想到利用勾股定理的逆定理找出△EE′C是直角三角形才是解题关键.勾股定理常用，同学们也比较容易想到，而勾股定理的逆定理，也是将边的关系转化为角的关系的常用方法，同学们可要用心哦！

（作者单位：江苏省常州市金坛区茅麓中学，常州市金坛区西岗中学）