相对传递路径分析方法及其在轿车车身振动分析中的应用

王增伟 朱平 覃智威 刘钊

（上海交通大学 上海市复杂薄板结构数字化制造重点实验室，上海 200240）

相对传递路径分析方法及其在轿车车身振动分析中的应用

王增伟 朱平 覃智威 刘钊

（上海交通大学 上海市复杂薄板结构数字化制造重点实验室，上海 200240）

提出一种基于全局传递率矩阵的相对传递路径分析方法，该方法建立传递路径分离模式，对分离模式下的响应进行预测，并计算出传递路径相对贡献度。针对轿车车身振动问题进行应用研究，选取发动机悬置安装点加速度和车内座椅安装处加速度作为振动传递分析的研究对象，试验结果表明，基于全局传递率矩阵的相对传递路径分析方法可以有效预测振动传递分离模式下的目标加速度，能够识别出贡献度较大的传递路径，验证了方法的工程可行性，为开展轿车车身NVH性能分析提供了可借鉴的方法和途径。

1 前言

传递路径分析方法（TPA）广泛用于分析和处理复杂机械系统的振动与噪声问题[1]。TPA主要分为经典TPA、基于子结构 TPA[2～4]和基于传递率矩阵TPA[5～9]。这些TPA方法基于“源—路径—目标”的分析模型识别研究系统的“源”和“路径”，计算传递路径对目标响应的“绝对”贡献量，但它们无法预测结构改进后系统目标响应变化的程度[10]。近年来，为了分析结构改变后的系统响应变化，学者们提出了传递路径分离技术[11]。路径分离技术可以预测传递路径断开后的目标响应，根据目标响应的变化程度计算传递路径的“相对”贡献量，为了区别于“绝对”TPA，基于路径分离技术的TPA称为“相对”TPA。研究表明，路径分离技术不需计算工况载荷就可以计算传递路径对目标响应的相对贡献度[12]，但是其需要拆卸结构，测试工作复杂。

本文将全局传递率矩阵和路径分离技术相结合，提出一种基于原位测量的传递路径相对贡献度计算方法，利用该方法进行了车身振动分析研究，并通过试验验证了该分析方法的工程可行性。

2 基于全局传递率矩阵的相对传递路径分析方法

假设所研究的物理系统是线性时不变的，将需要研究的子系统（或称为自由度）表示成一个离散的线性系统，如图1所示，图1中的s、i、j等代表子系统。基于“源—路径—目标”模型，TPA分析振动能量从载荷源通过不同路径传递到目标子系统的过程，而相对TPA则分析子系统之间连接断开后目标子系统响应变化的过程。全局-直接传递率矩阵方法（GTDT）是一种新型的TPA，其用全局传递率矩阵和直接传递率矩阵对目标子系统响应进行分解，当子系统之间的连接断开后，它可以预测系统在原载荷作用下的响应。

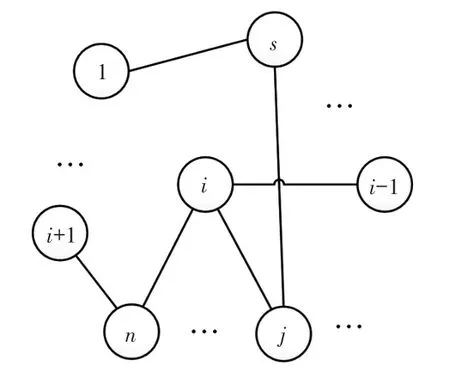
图1 n自由度的离散子系统

2.1 全局传递率矩阵和直接传递率矩阵

在GTDT方法中，子系统的响应可以表达为：

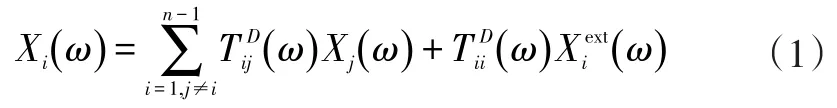
当其它子系统都被固定，只在子系统i上施加激励，则子系统i的响应记为则可以表示为：

直接传递率函数反映了子系统之间的连接情况，在实际测试中，通过测量全局传递率矩阵来计算直接传递率矩阵。当只有子系统j受到激励作用且所有子系统都没被固定住，子系统i与j的响应的比值称为j到i的全局传递率函数即

上式也可以写为：

式中，Hij为子系统j到子系统i的传递函数；Hjj为子系统j到自身的传递函数。

全局传递率函数表征一个受到激励的子系统的响应通过所有路径传递到另外子系统或自身的能力，它比较容易通过试验测得，且TGii=1。全局传递率函数与直接传递率函数有如下关系：

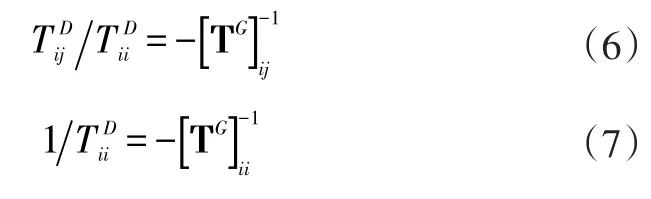
最后，系统的工况响应可以表达为：

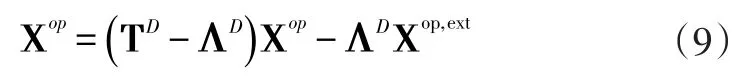
式中，ΛD是包含直接传递率矩阵对角元素的对角矩阵。

式（9）与式（1）是等价的，GTDT对系统响应的分解不需要解耦系统，更不需要测量任何力，它是一种效率高、可执行性强的TPA方法。

2.2 传递路径分离模型及响应预测

传递路径分离就是断开两个直接相连子系统之间的连接（物理连接，如发动机悬置等），如图2所示，子系统i和j之间的连接被断开。断开后的新系统在原系统载荷作用下，若目标子系统（假设为第n子系统）的响应变小，则认为i和j之间的传递路径对降低目标响应起正向作用，若目标子系统的响应变大，则认为i和j之间的传递路径对降低目标响应起负向作用。新系统和原系统中的目标响应之差表征断开路径对目标子系统响应影响的大小。这种通过断开子系统之间的连接以分析目标响应变化，进而找出对目标响应影响最大（正向）的传递路径的过程称为传递路径相对贡献度计算方法。下面阐述从原系统全局传递率矩阵推导传递路径分离后的新系统响应的过程。

将式（5）写成矩阵形式，即

式中，H是系统传递函数矩阵，它的逆矩阵为动刚度矩阵Z。

对全局传递率矩阵求逆可得：

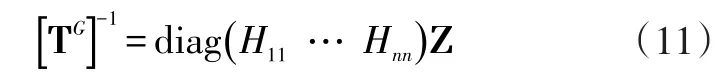
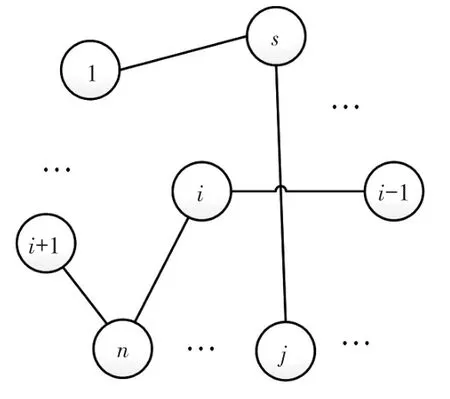
图2 传递路径分离模式

当子系统i和j之间传递路径被断开（图2），则系统变成一个新的n自由度系统。为了区别于原系统的变量，用符号“^”表示新系统变量。由离散系统的特性可知新系统的动刚度矩阵为：

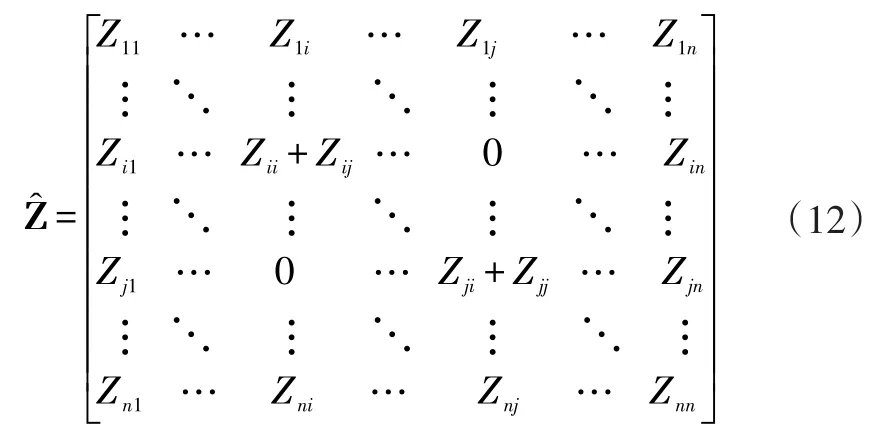
式中，Zst（第s行、第t列）为原系统动刚度矩阵的单元。

根据全局传递率矩阵的定义，新系统的全局传递率矩阵可表示为：

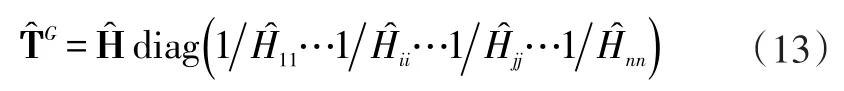
记原系统全局传递率矩阵的逆矩阵的第s行、第t列单元为即

为了计算新系统的全局传递率矩阵，定义转换矩阵为TGp，其逆矩阵为：

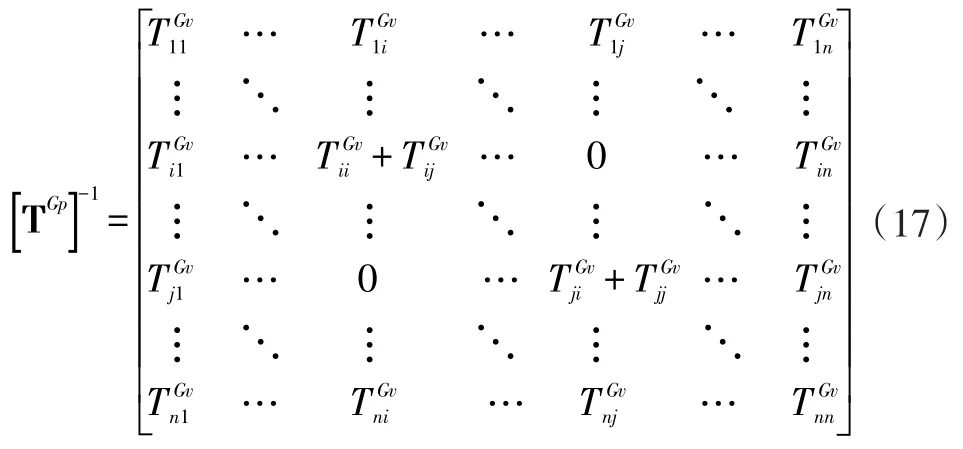
将式（17）展开后可得：

然后将式（12）带入式（18），得：

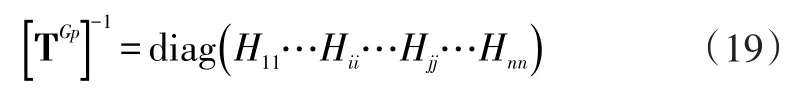
对式（19）求逆可得：

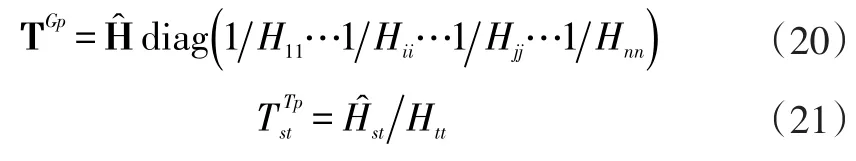
结合式（14），新系统的全局传递率函数则可以通过下式计算：

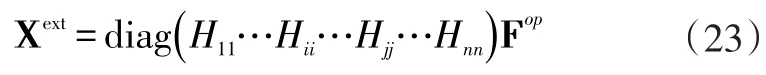
新系统的外部响应同样可以表达为：

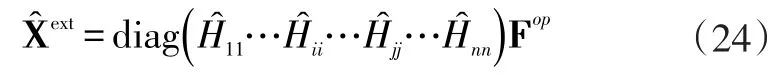
联立公式（23）和式（24）可得：

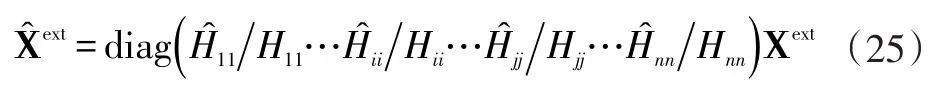
新系统中第s子系统的响应则可表达为：

这表明新系统中子系统的外部响应等于原系统的子系统外部响应乘以相应的转换矩阵单元。根据式（8）可知，新系统的响应为新系统全局传递率矩阵与新系统外部响应的乘积：

新系统的直接传递率矩阵可以通过新系统的全局传递率矩阵计算得到，最后新系统响应的分解公式可以表达为：

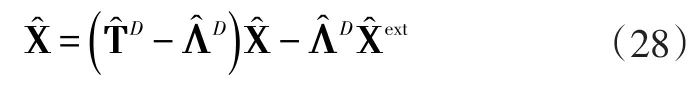
综上所述，新系统的响应可以通过原系统的响应和全局传递率矩阵计算得到，其计算流程如图3所示。首先测量原系统的响应和全局传递率矩阵；然后根据式（8）计算原系统的外部响应，并通过式（17）计算转换矩阵；再根据式（26）计算得到新系统的外部响应，用式（22）计算得到新系统的全局传递率矩阵；最后用式（27）计算得到新系统的响应，根据式（6）和（7）计算得到新系统的直接传递率矩阵，新系统的响应分解用式（28）表示。原系统的响应和全局传递率矩阵比较容易测量得到，新系统响应的计算不涉及任何载荷的测量，因此，基于全局传递率矩阵的相对传递路径分析方法是一种比较容易实施的方法[13]。

图3 传递路径断开后的系统响应预测流程

为了量化传递路径对目标子系统响应的影响，引入插入损失（Insertion Loss,IL）来表示由于传递路径的断开所引起系统响应变化的程度[14，15]。插入损失在电子系统中定义为当某一元件连入系统时传到负载的功率与原系统传到负载的功率比，插入损失用于相对TPA分析时，可定义为传递路径断开前、后目标子系统响应的有效值之比。插入损失大说明该路径在降低目标响应是主要的，根据定义，插入损失的计算式为：

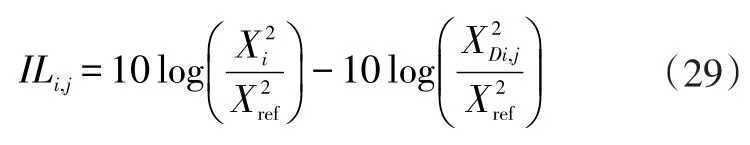
式中，ILi,j为分离第j条路径后子系统i响应的插入损失；Xi为原系统子系统i响应；XDi,j为分离第j条路径后目标子系统i响应；Xref为参考响应。

3 轿车车身振动分析应用

以某轿车为例，应用所提出的相对TPA对发动机引起车内结构振动的传递路径进行分析。该轿车的发动机通过3个悬置与车身连接，每个悬置考虑x、y、z等3个平动方向加速度，发动机到目标点的路径共有9条。验证后的车身有限元模型如图4所示，为了模拟发动机激励下的振动响应，在发动机质心位置施加20～200 Hz竖直方向的单位简谐力，动力总成惯性参数如表1所示。

图4 有限元分析模型

表1 动力总成惯性参数

选取座椅安装点竖直方向加速度作为目标响应，其加速度响应谱如图5所示，由图5可看出，该谱线中，在频率为137 Hz、147 Hz和176 Hz处出现比较明显的响应峰值，需要对这3个响应峰值进行传递路径分析。首先建立“发动机激励—悬置传递路径—目标加速度”模型，如图6所示，每个悬置有两个连接点，即发动机一侧和车身一侧连接点，每个连接点有3个平动自由度，因此整个模型共有19个自由度。建立TPA模型，如图7a所示，其路径分离结构如图7b所示。

运用相对TPA分别预测分离3个悬置的x-x、y-y、z-z传递路径后的目标加速度，计算插入损失值，如表2所示。由表2可知，在频率为137 Hz时，断开悬置1的x-x、z-z、悬置2的z-z和悬置3的y-y的传递路径可得到正的插入损失值，即断开这些传递路径后系统在原来激励作用下目标加速度会变小，其中悬置1的z-z方向传递路径具有最大值7.211 7；断开悬置1的y-y、悬置2的x-x、y-y和悬置3的x-x、z-z的传递路径得到负的插入损失值，即断开这些传递路径后系统在原来激励作用下目标加速度会变大，悬置3的z-z方向传递路径具有最小值-8.285 8。在频率为147 Hz时，悬置1的y-y方向、悬置3的y-y和z-z方向的传递路径具有负的插入损失值，悬置1的x-x方向具有最大值1.224 1，悬置3的z-z方向具有最小值-10.636 5。在频率为176 Hz时，悬置1的x-x、y-y、悬置3的x-x和y-y方向的传递路径具有正的插入损失值，悬置3的x-x方向具有最大值7.670 1，悬置2的z-z方向具有最小值-23.192 2。

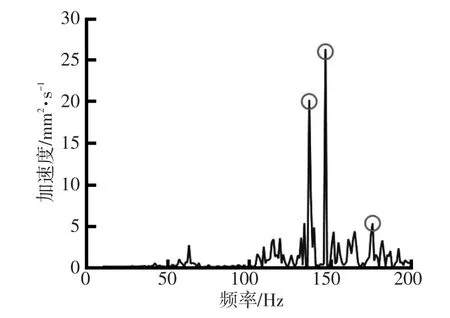
图5 座椅安装点加速度响应谱

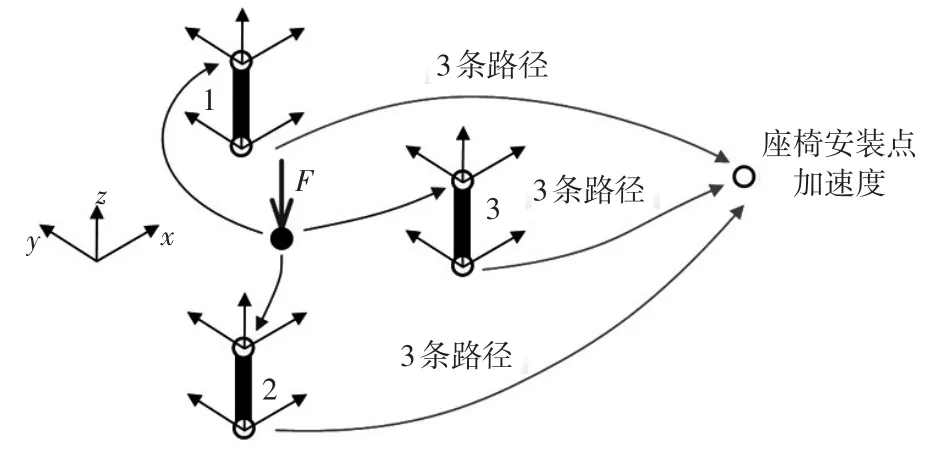
图6 传递路径模型

为了验证相对TPA分析结果的有效性，以频率为147 Hz为例，分别将3个悬置的3个方向动刚度设置为0，并计算目标加速度，结果如图8所示。其中横坐标值1～3分别代表将悬置1的x-x、y-y和z-z方向动刚度设置为0，4～6分别代表将悬置2的x-x、y-y和z-z动刚度设置为0，7～9分别代表悬置3的x-x、y-y和z-z动刚度设置为0。由图8可知，将悬置1的y-y、悬置3的y-y和z-z方向动刚度设置为0时，目标加速度比其原始值大，即它们的插入损失值为负，悬置3的z-z具有最大值；而当将其它方向的动刚度设置为0时，目标加速度小于其原始值，即它们的插入损失值为正。由此可知，图8中的目标加速度响应与表2中频率为147 Hz时的插入损失值是一致的，这说明相对TPA可以准确计算出路径断开后的目标响应，并计算出不同路径对目标响应的相对贡献度。

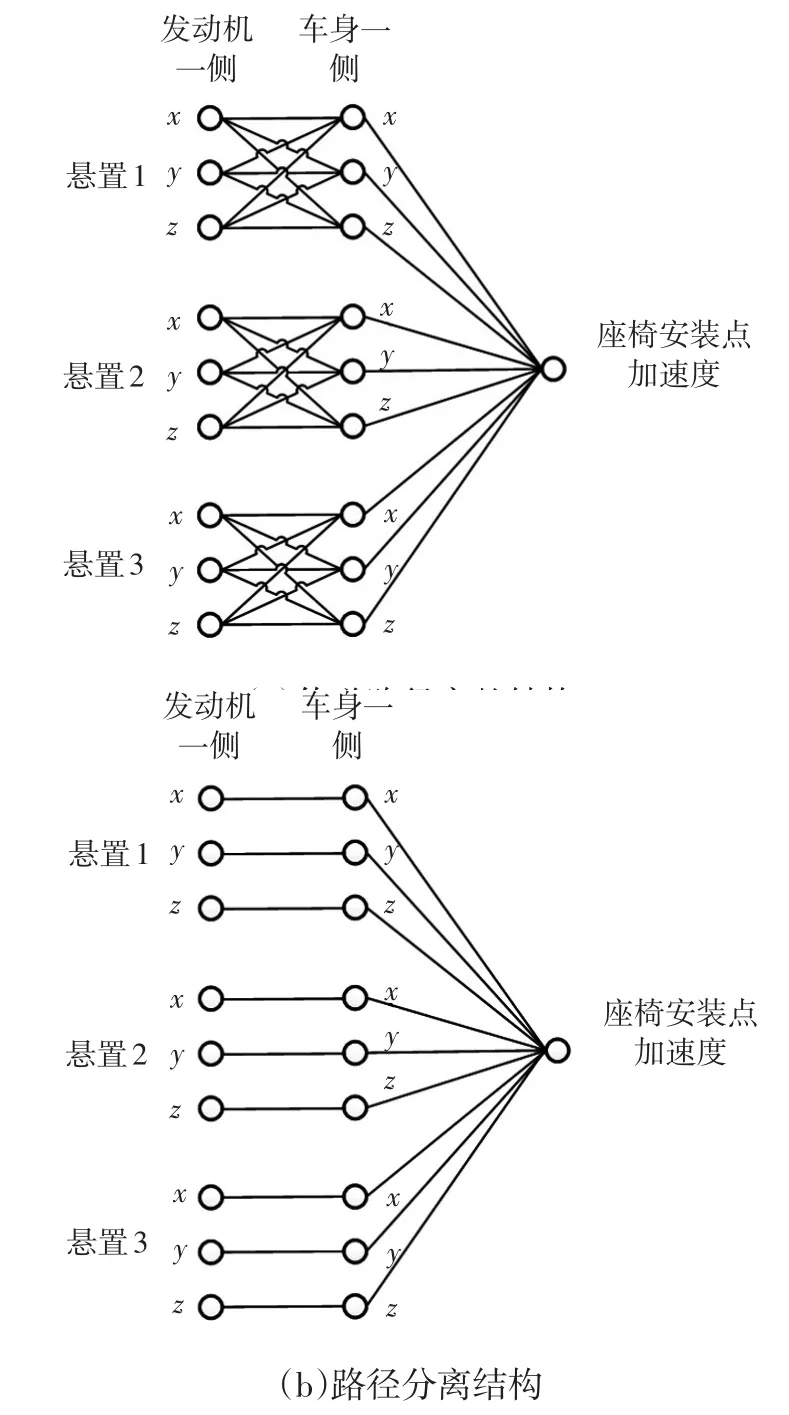
图7 相对TPA模型

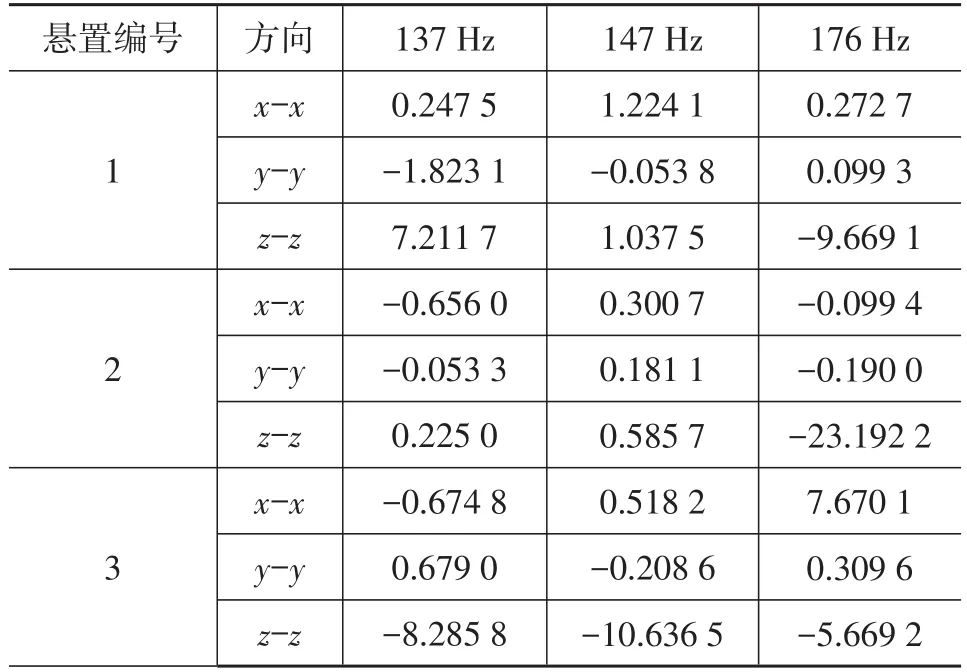
表2 插入损失值

图8 动刚度设置为0后的座椅安装点加速度

根据计算得到的插入损失值对9条传递路径进行排序，同时采用经典TPA对9条传递路径进行分析，计算传递路径的绝对贡献度，并对传递路径的重要性进行排序，频率为147 Hz时的路径排序结果如表3所示。由表3可知，相对TPA前3个最重要传递路径为悬置1的x-x、z-z和悬置2的z-z，而经典TPA前3个最重要传递路径为悬置3的z-z、悬置2的y-y和z-z。对比传递路径排序结果可知，相对TPA的传递路径重要性排序与经典TPA的排序结果不同。这是由于相对TPA（相对贡献度）表征的是传递路径分离后目标加速度响应的变化程度，而经典TPA（绝对贡献度）表征的是从载荷点通过传递路径上传递到目标加速度响应的能量的大小。相对TPA能够在不需要拆分动力系统的情况下预测结构改变后的目标响应，并计算传递路径相对贡献度，指出了结构改进的方向以降低目标响应，是对以经典TPA为代表的传递路径绝对贡献度分析方法的重要补充和对TPA的完善。

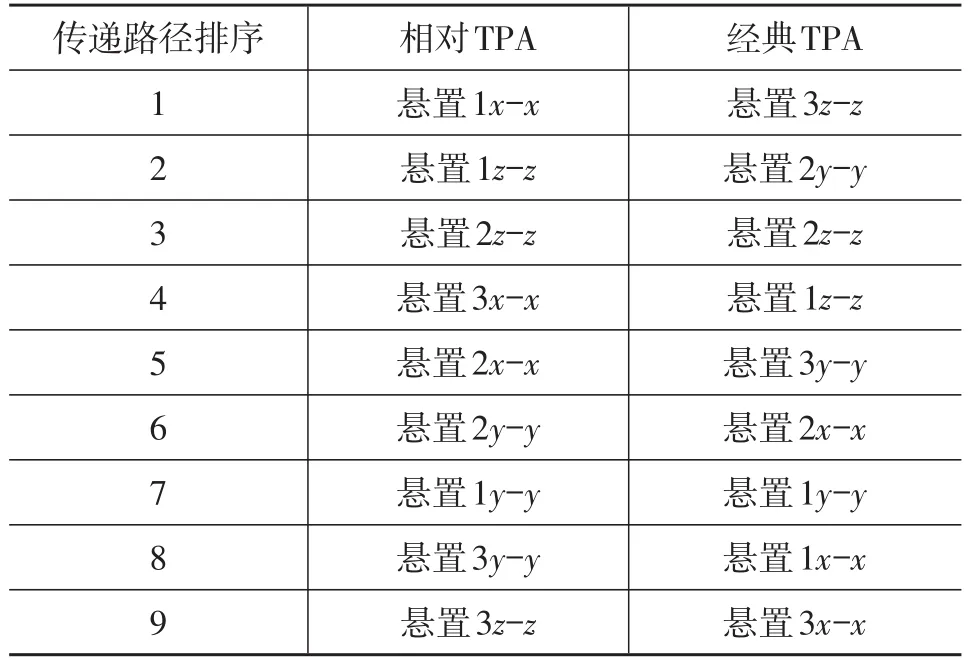
表3 频率为147 Hz时传递路径重要性排序

4 结束语

结合全局传递率矩阵和路径分离技术，提出了一种原位测量的相对TPA，可以预测传递路径分离后的系统响应。在发动机引起车身振动传递的案例中，采用该方法进行了振动传递分析应用研究，结果表明，相对TPA能够在不需要拆分动力系统的情况下预测结构改变后的目标响应，并计算传递路径相对贡献度，指出了结构改进的方向，是对以经典TPA为代表的传递路径绝对贡献度分析方法的重要补充和对TPA的完善。通过车身振动案例验证了该方法的工程可行性，并为开展轿车车身NVH性能分析提供可借鉴的新方法和途径。

1 郭荣，万钢，左曙光.燃料电池轿车车内噪声传递路径分析研究.汽车工程，2007，29（8）：635～641.

2 Rixen D J,Boogaard A,et al.Vibration source description in substructuring：A theoretical depiction.Mechanical Systems and Signal Processing,2015,60～61,498～511.

3 Klerk D de,Rixen D.Component transfer path analysis method with compensation for test bench dynamics.Mechanical Systems and Signal Processing,2010,24,6,1693～1710.

4 M V van der Seijs,Klerk D de,DRixen J.General framework for transfer path analysis：History,theory and classification of techniques.Mechanical Systems and Signal Processing,2015,68～69,217～244.

5 乔宇锋，黄其柏，李天匀.工况传递路径分析(OPA)方法在应用中的缺陷.噪声与振动控制，2010,1（5）：132～136.

6 Gajdasty P,Janssens K,Desmet W,et al.Application of the transmissibility concept in transfer path analysis.Mechanical Systems and Signal Processing,2010,24,7,1963～1976.

7 Klerk D D,Ossipov A.Operational transfer path analysis theory,guideline and tire noise application.Mechanical Systems and Signal Processing,2010,24,1950～1962.

8 郭荣，裘剡，房怀庆，等.频域传递路径分析方法(TPA)的研究进展.振动与冲击，2013,32（13）：49～54.

9 Klerk D,Dennis,Lohrmann,et al.Application of operational transfer path analysis on a classic car.NAG/DAGA2009,2009.

10 Zengwei Wang,Ping Zhu.Response prediction for modified mechanical systems based on in-situ frequency response functions：Theoretical and numerical studies.Journal of Sound and Vibration,2017,400,417～441.

11 Inoue A,Singh R，Fernandes G A.Absolute and relative path measures in a discrete system by using two analytical methods.Journal of Sound and Vibration,2008,313,3-5,696～722.

12 Guasch O.Direct transfer functions and path blocking in a discrete mechanical system.Journal of Sound and Vibration,2009,321,3-5,854～874.

13 Zengwei Wang,Ping Zhu,Jianxuan Zhao.Response prediction techniques and case studies of a path blocking system based on Global Transmissibility Direct Transmissibility method.Journal of Sound and Vibration,2017,388,363～388.

14 赵薇，周娜，张义民.振动传递路径系统的路径插入损失分析.东北大学学报（自然科学版），2015,36（2）：250～258.

15 Zengwei Wang,Ping Zhu.A system response prediction approach based on global transmissibilities and its relation with transfer path analysis methods.Applied Acoustics,2017,123,29～46.

（责任编辑 文 楫）

修改稿收到日期为2017年7月8日。

Relative Transfer Path Analysis Method and Its Application in Auto Body NVH Analysis

Wang Zengwei,Zhu Ping,Qin Zhiwei,Liu Zhao
（Shanghai Key Laboratory of Digital Manufacture for Thin-Walled Structures,Shanghai Jiaotong University,Shanghai 200240）

A relative transfer path analysis method based on global transmissibility matrix is proposed in this paper,that establishes transfer path separation mode and predicts the system response under this mode.The relative transfer path contribution is then calculated.The method is applied to passenger car body NVH issue,in which the acceleration at engine mounting point and seat mounting point are chosen as objects of study.The results show that the proposed method can predict the target acceleration under the vibration transfer separation mode effectively,recognize the transfer path with greater contribution.Engineering feasibility of this method is proved,which provides referential methods and approach for passenger car body NVH analysis.

Vehicle bodyvibration,Transferpath,Transmissibilitymatrix,Relative contribution

车身振动 传递路径 传递率矩阵 相对贡献度

U461.4 文献标识码：A 文章编号：1000-3703（2017）09-0034-06