例谈叠加电场强度的求解

■浙江省温岭中学高三（2）班 叶佳木

例谈叠加电场强度的求解

■浙江省温岭中学高三（2）班 叶佳木

电场强度是描述电场力的性质的物理量,是电场中最基本、最重要的概念之一。求解单个电场的场强相对比较容易,当遇到求解多个电场的叠加电场强度时就需要注意了。下面将求解叠加电场强度的方法进行归纳总结,与同学们共勉。

1.叠加原理:多个电荷在空间某处产生的电场为各电荷在该处所产生的电场强度的矢量和。

2.运算法则:平行四边形定则。

3.计算叠加电场强度常用的方法:

(1)电场叠加合成法:多个电场在空间某点产生的合场强等于每个电场单独存在时在该点产生的场强的矢量和。这种方法是求解叠加电场的电场强度的理论通用方法,在求解实际问题时,若能够采用更加简单快捷的方法,则可以优先采用其他方法,以节省时间、锻炼思维。

(2)对称法:利用对称法分析解决叠加场强问题可以避免复杂的数学演算和推导,直接抓住问题的实质,获得出奇制胜之效。比如,均匀带电的球壳在球外空间产生的电场等效于电荷集中于球心处产生的电场。如图1所示,在半球面AB上均匀分布着正电荷,总电荷量为q,球面半径为R,CD为通过半球顶点与球心O的轴线,在轴线上有M、N两点,OM=ON=2R。已知M点的场强大小为E,求N点的场强大小。这道题就可以运用对称法顺利求得N点的场强大小为(同学们不妨试试看)。

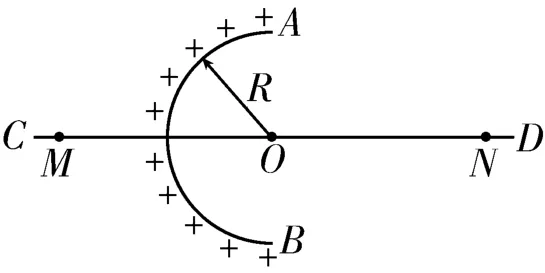
图1

(3)微元法:微元法是将研究对象分割成若干微小的单元,或从研究对象上选取某一“微元”加以分析,从而达到化曲为直的目的,使变量、难以确定的量转化为常量、容易确定的量,进而使问题获解。在求解叠加电场强度时,若能适时使用微元法往往会获得意想不到的效果。

(4)等效法:等效法的实质是在效果相同的情况下,利用物理问题中某些相似或相同效果进行知识迁移的一种方法。利用等效法解决叠加电场强度问题可以将较复杂的电场问题转化为较简单易行的问题。

(5)补偿法:当需要求解一个不规则带电体所产生的电场时,因为没有现成的公式可以直接套用,所以就需要变换思维角度,采用补偿法解决了。比如,如图2所示,半径为R的球体上均匀分布着电荷量为Q的电荷,在过球心O的直线上有A、B两点,O和B、B和A间的距离均为R。现以OB为直径在球内挖一球形空腔,求A点处场强的大小。显然,本题的物理模型是均匀带电球壳在球外空间产生的电场,然而因为球内被挖去了一个球形空腔,成了一个不规则带电体,所以要想顺利求解就必须采用补偿法了。将这个球形空腔补全,就形成一个电荷均匀分布的完整带电球体,完整带电球体在A点处产生的场强被挖去的小球的电荷量在A点处产生的场强E'=这样,求解不规则带电体所产生的场强问题就变为求解两个规则带电体所产生的场强的矢量和问题了。因此所求场强大小为

图2

注意:(1)电场强度为矢量,在求解叠加电场强度时千万不可忽略场强的方向;(2)在由点电荷形成的电场中,不要把场源电荷和试探电荷混淆;(3)应用计算匀强电场的场强时,d是指两点沿电场方向的距离,而不是两点间的距离。

(责任编辑 张 巧)