基于Mann-Kendall突变检验与ARIMA模型的臭氧水平预测

仲 露，夏 杰，赵良娟，陈富媛,何东平

(1.安徽财经大学财政与公共管理学院，安徽 蚌埠 233030;2.安徽财经大学统计与应用数学学院，安徽 蚌埠 233030)

基于Mann-Kendall突变检验与ARIMA模型的臭氧水平预测

仲 露1，夏 杰2，赵良娟2，陈富媛2,何东平1

(1.安徽财经大学财政与公共管理学院，安徽 蚌埠 233030;2.安徽财经大学统计与应用数学学院，安徽 蚌埠 233030)

目的针对未来50年臭氧水平预测，首先以南半球为例，从美国航空航天局(NASA)中获取1985—2015年臭氧含量的数据，按季节分为4类。方法运用Mann-Kendall突变检验的方法,利用MATLAB软件对数据进行检验，应用ARIMA模型对不同季节分别进行预测，考虑到影响大气中臭氧含量的3类因素：相关卤烃浓度、氟氯烃浓度以及氮氧化物浓度，以它们为自变量，臭氧含量为因变量做多元线性回归模型。结果全球30年的春季未出现大的突变，全球30年夏季未出现大的突变，全球30年秋季未出现大的突变，全球30年冬季未出现大的突变；其次，残差序列已经可以认为是一个纯白噪声的序列。结论未来50年臭氧含量不会一直减少，因变量与自变量成反比，即这些物质的排放量逐渐减少，未来50年大气中的臭氧含量缓慢升高至平稳。

臭氧水平；ARIMA时间序列预测模型；多元线性回归模型；M-K突变检验

在距离地球表面20～40 km的高空平流层中的臭氧层浓度高达百万分之十，占大气中总臭氧的90%以上。高层大气中存在着臭氧的形成和分解两种光化学过程，这两种过程达到动态平衡，使臭氧含量长期保持在相应范围，形成了一个浓度相对稳定的臭氧层。有资料观测分析表明，从1985至1995的10年间，北半球上空大气臭氧损耗平均达到5%，南半球上空臭氧损耗平均达3%，并且这种臭氧损耗趋势还在继续。科学家们认为，人工合成的一些含氯和含溴的物质是造成南极臭氧洞的元凶。最典型的是氟氯碳化物(CFCs，俗称氟氯昂)和含溴化合物哈龙(halons)。这些化合物在对流层是化学惰性的，十分稳定，不能通过一般的大气反应去除。在平流层内，强烈的紫外线照射使CFCs和halons发生解离，释放出高活性的原子态的氯和溴，氯原子自由基和溴原子自由基就是破坏臭氧层的主要物质。早在20世纪60年代,Junge提出了一套对流层臭氧产生的经典理论,认为对流层的臭氧主要来源于平流层的动力下传,平流层产生的臭氧下传到对流层成为对流层臭氧的源，从而保持对流层臭氧的平衡,Junge的理论强调的是对流层动力下传，以及平流层与对流层之间的相互交换。20世纪70年代Levy Crutzen等提出了臭氧主要是大气光化学反应的结果。随着对臭氧研究的深入,1983年Brewer最先提出了非甲烷碳氢化合物(NMHC)在大气光化学臭氧形成过程中的作用。在化学机理中,考虑的有机物种类越来越多,1994年Chameides提出了大陆尺度(metro-agro-plexes，MAP)的概念,讨论了区域尺度的城市工农业排放造成的臭氧对全球生态系统的可能影响。本文对未来五十年的臭氧水平进行预测，并得到相关结论。

1 基于MANN-KENDALL突变检验模型对臭氧水平数据的检验

1.1 研究思路

MANN-KENDALL(M-K)法是一种非参数统计检验方法。其优点是不需要样本遵从一定的分布，也不受少数异常值的干扰，更适用于分类变量和顺序变量，计算也比较方便，现已广泛应用于降水、径流、气温等水温气象参数趋势分析等。

1.2 研究方法

M-K[1]是在气象学和气候学中经常用来进行突变检验的一种方法。具体方法如下：

(1)设原始时间序列为y1,y2,…,yn,mi表示第i个样本yi大于yj(1≤j≤i)的累积数，定义统计量：

(2)在原序列随机独立等假设下，dk的均值和方差分别为

E(dk)=k(k-1)/4,var(dk)=k(k-1)(2k+5)/72

(3)将上面公式的dk标准化，得：

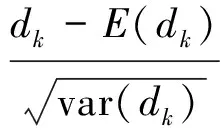
(4)UFk组成一条UF曲线，通过信度检验可得出其是否有明显的变化趋势。

(5)把此方法引用到反序列中，计算得到另一条曲线UB， 则两条曲线在置信区间内的交点确定为突变点。

(6)给定显著性水平α=0.05，则统计量UF和UB的临界值为±1.96。UFgt;0， 表示序列呈上升趋势；反之，表明呈下降趋势，UF大于或小于±1.96，UF表示上升或下降趋势明显。

1.3 模型的求解

利用从美国航天局(NASA)获取的1985—2015年臭氧含量数据，运用MATLAB软件对上述模型求解，做出它们的Mann-Kendall突变检验图(图1～4)。

在Mann-Kendall突变检验图[1]中，如果c1和c2在临界值1.96(α=0.05))之间有一个显著的交点，且c2上升超过了+1.96或下降低于-1.96，则可以认为序列产生了突变，前者表示臭氧的含量由低向高突变，后者表示臭氧的含量由高向低突变，并且这个交点就是突变的开始。

从图1～4可见，全球30年的春季，未出现大的突变，全球30年夏季未出现大的突变，全球30年秋季未出现大的突变，全球30年冬季未出现大的突变。

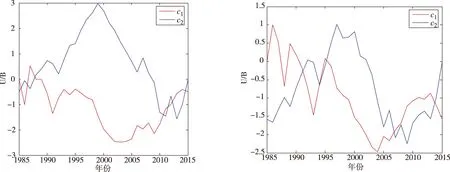
图1春季突变检验图图2夏季突变检验图

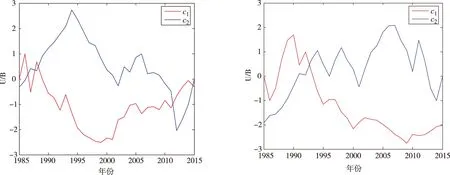
图3秋季突变检验图图4冬季突变检验图

2 基于ARIMA模型对未来50年不同季节臭氧水平预测

2.1 研究思路

ARIMA模型是时间序列分析中最常用的模型之一，ARIMA模型提供了一套有效的预测技术，在时间序列预测中具有广泛的应用[2]。ARIMA模型又称自回归移动平均模型。它是将非平稳时间序列转化为平稳时间序列，然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。ARIMA模型将预测指标随时间推移而形成的数据序列看作是一个随机序列，这组随机变量所具有的依存关系体现着原始数据在时间上的延续性，它既受外部因素影响，又有自身变动规律。具体研究思路流程如图5所示。

图5 研究思路流程图

2.2 研究方法

(1)AR(p)(p阶自回归模型)

xi=δ+φ1xi-1+φ2xi-2+…+φpxi-p+ui

其中ui是白噪声序列，δ是常数(表示序列数据没有0均值化)

AR(p)的特征方程是：

φ(L)=1-φ1L-φ2L2-…-φpLp=0

式中L为延迟算子，AR(p)平稳的充要条件是特征根都在单位圆之外。

(2)MA(q)(q阶移动平均模型)

xi=μ+μi+θ1μi-1+θ2μi-2+…+θqμi-q

其中ui是白噪声过程，MA(q)具有平稳性，由于MA(q)是由ui本身和q个ui的滞后项加权平均构造出来的，因此它是平稳的。

(3)ARMA(p，q)(自回归移动平均过程)

xi=φ1xi-1+φ2xi-2+…+φpxi-p+δ+ui+θ1ui-1+θ2ui-2+…+θqui-qΦ(L)xi=(1-φ1L-φ2L2-…-φpLp)xiΦ(L)xi=δ+(1+θ1L+θ2L2+…+θqLq)ui

ARMA(p,q)平稳性条件是方程Φ(L)=0的根都在单位圆外。

(4)ARIMA(p,d,q)(单整自回归移动模型)

Δxi=xi-xi-1=xi-Lxi=(1-L)xi

则wt是平稳序列，于是可对wt建立ARMA(p,q)模型，所得到的模型称为xi～ARIMA(p,d,q)模型的形式是：

wt=φ1wi-1+φ2wi-2+…+Φpwi-p+δ+ui+θ1ui-1+θ2ui-2+…+θqui-q

由此可转化为ARIMA模型。[3]

2.3 模型的求解

根据以上分析结果，利用EVIEWS软件预测未来50年的臭氧层在不同季节下含量的具体情况，见表1。

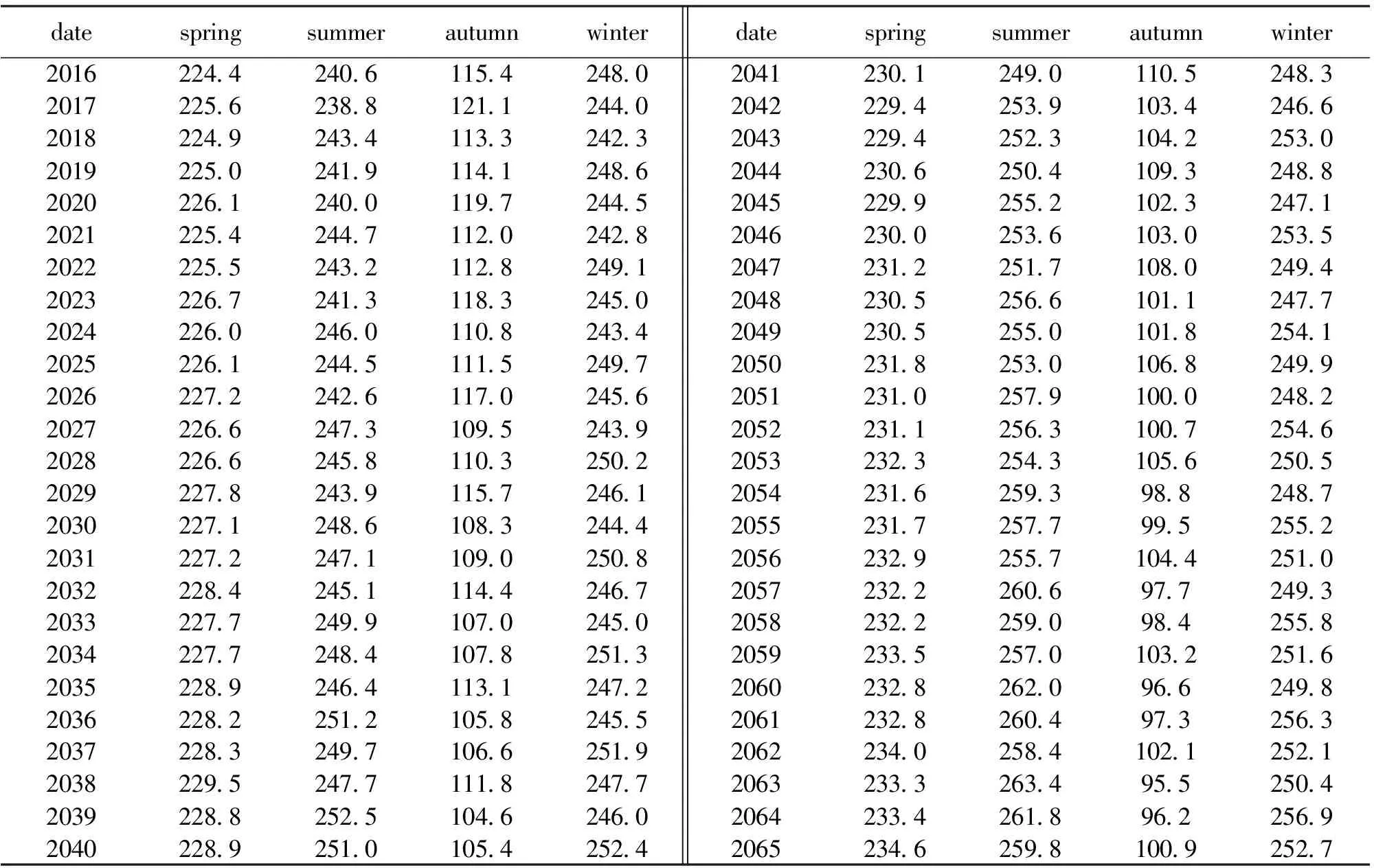
表1 不同季节下的臭氧层含量(单位：mg·L-1)

再分别对春、夏、秋、冬4个季节的预测结果的数据做出自相关图[4]，如图6～9所示。

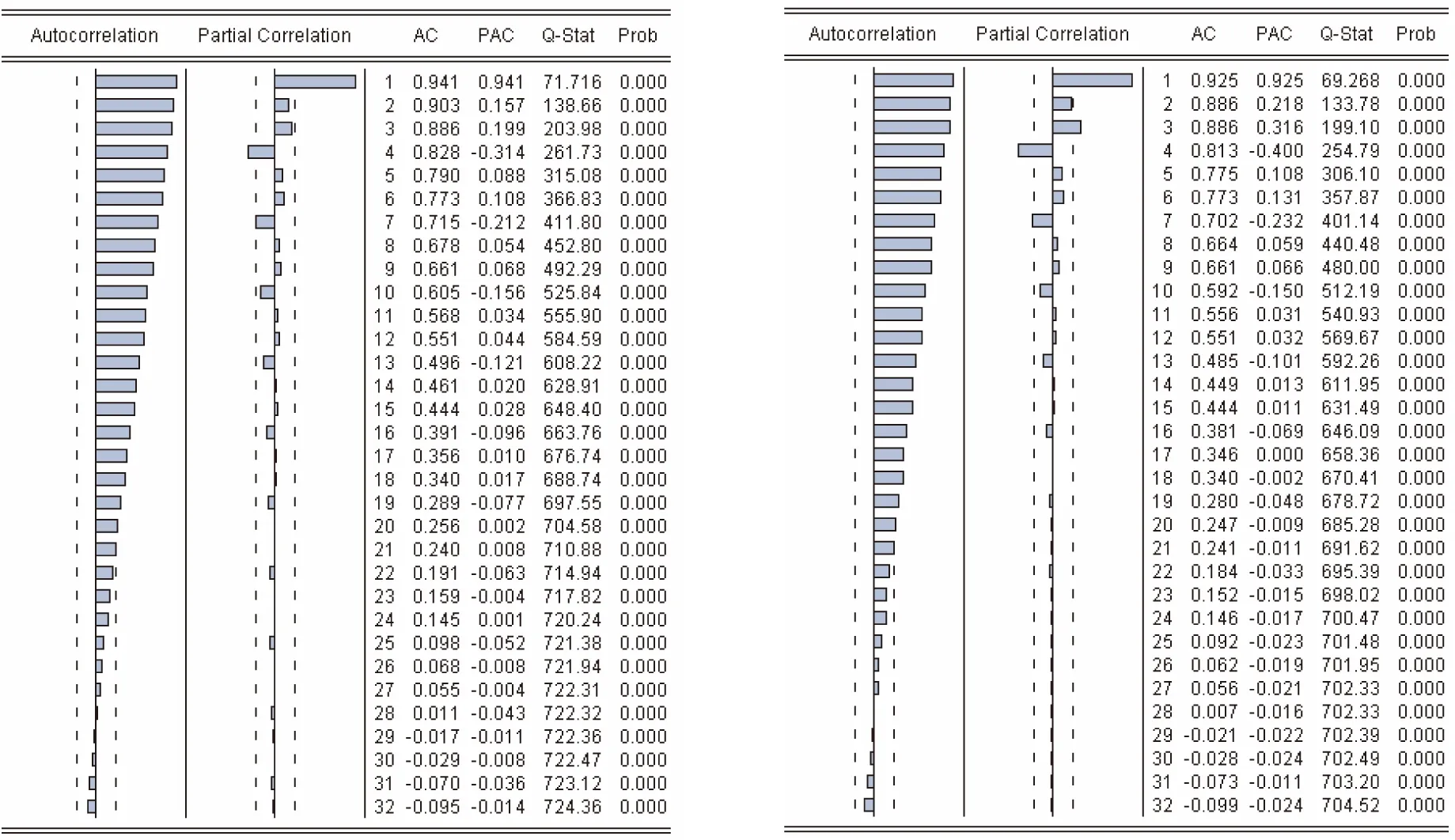
图6春季自相关图图7夏季自相关图

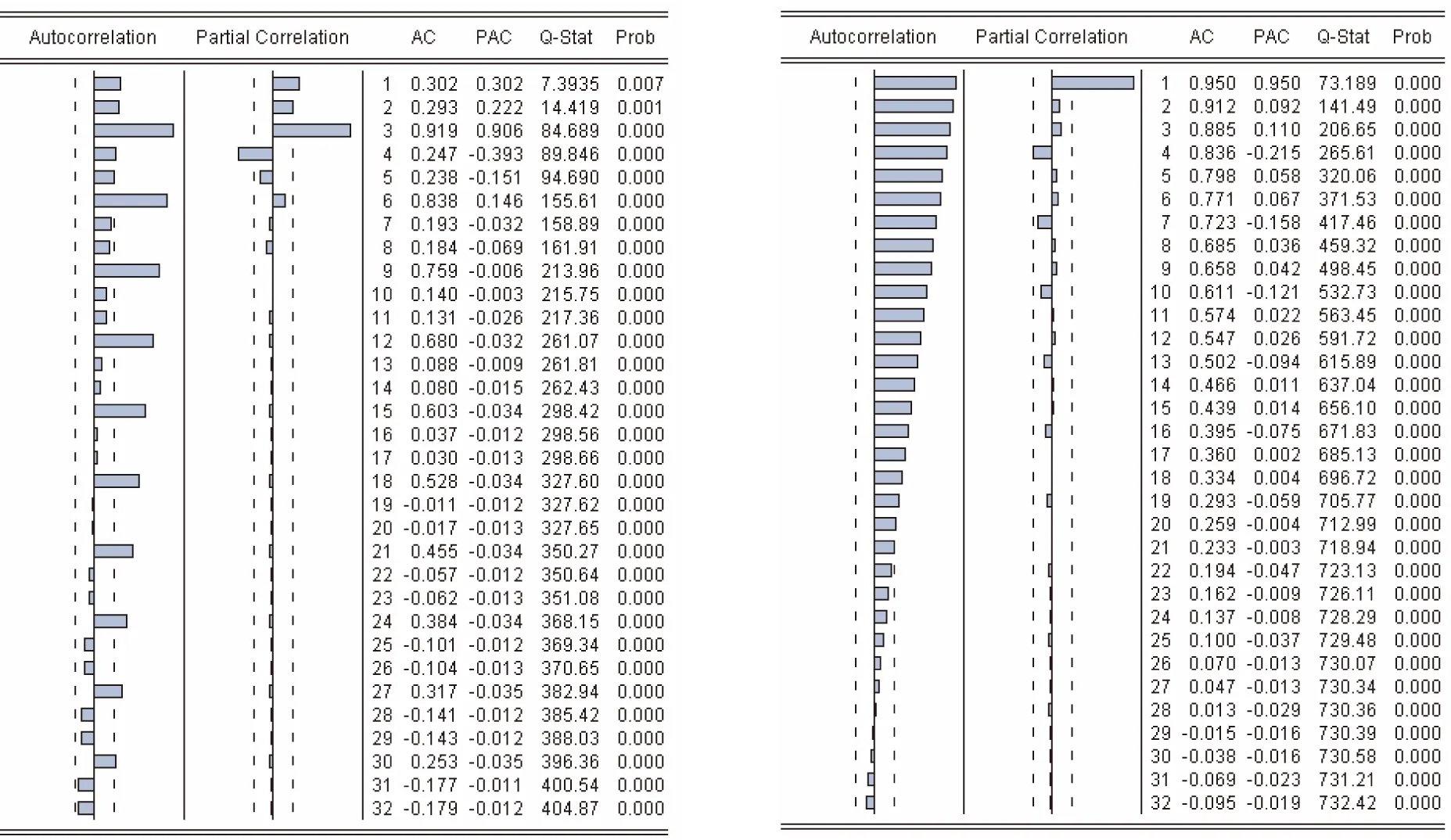
图8秋季自相关图图9冬季自相关图

通过这一检验，看到残差序列已经可以认为是一个纯白噪声的序列[5]，说明模型已经将有用的信息充分提取了。

3 基于多元线性模型臭氧平均浓度与各因素关系研究

3.1 研究思路

1987年43个国家的代表签署了《蒙特利尔议定书》，参与者同意冻结氟氯烃生产，停留在1986年的水平，在1999年将其产量缩减到原来的50%，即大气层中臭氧的水平不会再继续减少下去。选取1985年、1992年、2000年、2007年以及2015年的数据，画出折线图进行比较得出，每一年大气层中的臭氧含量波动的幅度相近，尤其在秋季臭氧总量在下降，到冬季臭氧总量有所回升[6]。并且在1992年以及2007年这两年的臭氧总量较低，即大气层中的臭氧由于氟氯烃的排放而有损失，2015年的数据虽然没有1985年的高但没有持续下降，由此可以看出《蒙特利尔议定书》的颁布起到了一定的限制作用。利用多元线性回归的方法，对臭氧平均浓度与氟氯烃浓度和氮氧化物浓度进行研究[7]。

3.2 研究方法

在研究3个变量：相关卤烃浓度、氟氯烃浓度、氮氧化物浓度对臭氧平均浓度影响的时候，首先通过SPSS对各变量之间的关系进行分析得到各个自变量之间的系数相关性[8]，见表2。

表2 系数相关性

在SPSS软件中做臭氧平均浓度与其他3个自变量的多元线性回归[9]，得到的结果，见表3～4。

表3 回归系数表

表4 变异数分析

从回归结果可以看出，F检验表明回归方程线性关系显著，且氟氯烃浓度，氮氧化物浓度与相关卤烃浓度均通过检验。从回归标准化残差的常态P-P图(图10)可以看出：回归标准残差几乎都在P-P图的对角线上，因此可以认为残差是服从或近似服从正态分布的。

由此可以确定回归方程为

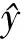
事实上，并不能由上式代入未来50年的氟氯烃浓度、氮氧化物浓度与相关卤烃浓度从而得到当年的臭氧浓度，因为预测本就存在许多不确定因素，存在许多假设，只有在特定条件下才能得到该结果。

图10 常态P-P图

3.3 研究结果

同时，可以观察到臭氧平均浓度与氟氯烃浓度和氮氧化物浓度成反方向变动，这是符合认知与调查分析的，但臭氧浓度与相关卤烃浓度成正反向变动，这并不符合人们的认知。事实上，当对3种影响因素分别与臭氧平均浓度做回归分析时，均呈反方向变动，所以推理分析得出：当氟氯烃、氮氧化物与相关卤烃3种物质共同存在的时候，会发生某种化学反应，相关卤烃浓度上升反而使得臭氧平均浓度升高，但是由于其系数比较小，可以推断影响效果并不明显。[10]

4 结论与讨论

随着经济社会的发展，人们对环境质量更加重视，光化学烟雾成为影响城市环境空气质量的重要因素。本文研究结果表明，臭氧浓度随季节变化趋势明显，春、夏季臭氧浓度较高，秋季臭氧浓度次之。臭氧浓度在每天中呈单峰型的变化规律，白天臭氧浓度处于较高水平，夜间臭氧浓度较低。臭氧浓度日变化随季节变化明显。与冬季相比，春、夏和秋季臭氧浓度的日变化幅度比较大，臭氧浓度分布比较分散。通过对臭氧浓度变化的研究，得到了未来50年的臭氧含量不会一直减少的结论；对于影响大气中臭氧含量的3类因素：相关卤烃浓度、氟氯烃浓度以及氮氧化物浓度，发现臭氧含量与各个因素成反比，即这些物质的排放量逐渐减少，未来50年大气中的臭氧含量缓慢升高至平稳。保护臭氧层的任务迫在眉睫，人们应当减少那些对臭氧层损害较大的物质的使用，同时鼓励推广使用对环境和人类无害的替代物质。这样，臭氧层损耗的问题将在人类的努力下渐渐消逝。

[1] 王会祥,唐孝炎.臭氧层损耗:人类面临的重大环境问题:1995年诺贝尔化学奖简介[J].大学化学,1996,11(03):6-10.

[2] 王俊萍.大气臭氧层的形成及破坏机理的研究[J].内蒙古石油化工,2006,9(05):7-8.

[3] 岳超,王少鹏,朱江玲.2050年中国碳排放量的情景预测:碳排放与社会发展IV[J].北京大学学报,2010,46(04):517-524.

[4] 胡璇.对地球“两极”臭氧层严重破坏的研究[J].安徽农业科学,2015,43(04):263-265.

[5] 王振友.多元线性回归统计预测模型的应用[J].理论新探,2008,5(05):46-47.

[6] 刘志威,朱家明,陈媛,等.基于高斯烟羽扩散模型的蚌埠市空气质量的研究[J].赤峰学院学报(自然科学版),2016,32(01):133-137.

[7] 汪雅倩,朱家明,钱舒婷,等.合肥市PM2.5影响因素及分布演变规律的定量分析[J].商丘师范学院学报,2016,32(03):1-6+16.

[8] 单欣,朱家明,陆玉,等.基于扩散模型的京津冀地区空气污染研究[J].河南工程学院学报(自然科学版),2016,28(01):52-57.

[9] 徐路,朱家明,宣琳,等.基于高斯扩散模型PM2.5污染物的成因与演变[J].佳木斯大学学报(自然科学版),2016,34(02):293-296+299.

[10] 何玲,朱家明,林根,等.基于高斯扩散模型PM2.5污染的影响因素分析[J].丽水学院学报,2016,38(02):42-48.

[责任编辑：刘志媛英文编辑：刘彦哲]

OzoneLevelPredictionBasedonMann-KendallMutationTestandARIMAModel

ZHONGLu1,XIAJie2,ZHAOLiang-juan2,CHENFu-yuan2,HEDong-ping1

(1.Institute of Finance and Public Management,Anhui Finance and Economics University,Bengbu,Anhui 233030,China;2.Institute of Statistics and Applied Mathematics,Anhui Finance and Economics University,Bengbu, Anhui 233030,China)

ObjectiveTo study the forecast of ozone level in the next 50 years,the data of ozone in the 1985-2015 in the southern hemisphere were obtained from NASA.MethodsThe data were analyzed by Mann-Kendall mutation test.And the ARIMA model was used to predict the different seasons.The three factors affecting the ozone content in the atmosphere were taken into account,such as the relevant halocarbon concentration,HCFC concentration and nitrogen oxide concentration.By taking them as the independent variables and the ozone content as the dependent variable,multiple linear regression model was conducted.ResultsFirst in the four seasons for 30 years of the global,no major mutations were found;second,the residual sequence showed a sequence of purely white noise.ConclusionOzone content will not be reduced in the next 50 years.The dependent variable is inversely proportional to the independent variable,that is,the emission of theses substances will gradually decrease and the ozone content in the atmosphere will rise slowly in the next 50 years.

ozone level;ARIMA time series prediction model;multiple linear regression model;Mann-Kendall mutation test

来稿日期：2017-01-13

国家自然科学基金资助项目(11601001)

仲露(1996-)，女，安徽天长人，安徽财经大学财政与公共管理学院在读学生，研究方向：税收学。

何东平(1971-),安徽安庆人，安徽财经大学财政与公共管理学院讲师，硕士，研究方向:公共管理与社会调查。

X 515

A

10.3969/j.issn.1673-1492.2017.11.004