大气污染排放物的最优控制研究
徐 芹
(甘肃中医药大学定西校区 理科教学部,甘肃 定西 743000)
大气污染排放物的最优控制研究
徐 芹
(甘肃中医药大学定西校区 理科教学部,甘肃 定西 743000)
针对目前大气污染严重影响人类健康的问题,列举实例,通过定量分析建立了最优化数学模型,经LINGO求解得出在不同的污染点源分别采用斜板沉淀槽、喷雾洗涤器、多级除尘器等控制方法,可以1 871 114元/年将污染物削减80%.结果表明该优化算法执行效率高,速度快,结果精确,且能够以最有效的控制方法,最低的成本把大气污染物总排放量削减到国家规定的标准,进而为有关部门制定更加有效、经济的污染物控制和削减方案提供了科学的依据,具有一定的参考价值和指导意义.
总悬浮颗粒物;削减度;控制方法;允许排放量
0 引言
近几年,大气污染严重影响着我国大部分地区,特别是2016年入冬后,时间长且波及范围极广的雾霾天气,致使多地航班延误甚至取消,许多学校不得不停止学生的户外活动.可见大气污染已成为影响经济发展、危害国民健康的隐形杀手.如何降低污染,提高空气质量,备受社会各界人士的关注.刘正广[1]、何吉成[2]、史宇[3]等对近 20 年大气污染的特征、趋势等做了一定的分析,并提出了一些防治措施.2015年8月29日,在第十二届全国人民代表大会常务委员会上,《中华人民共和国大气污染防治法》正式修订通过,该法规进一步彰显出国家防治大气污染,保护和改善生活环境和生态环境,保障人体健康的决心和力度[4].国家投入了大量的专项治理资金,那么如何节省治理资源,加大治理效率,以使防治工作取得事半功倍的效果,成为人们关注的热点之一.本文以实际问题为例,给出了大气污染排放的最优控制方案,解决了以下三个问题:
1)在不同的大气污染排放点源,采取何种控制方式最有效;
2)如何把大气污染物总排放量削减到国家规定的标准;
3)以最小的费用保证污染物控制措施高效实施.
1 问题描述
就种类而言,我国的大气污染物主要包含二氧化硫、总悬浮颗粒物、氮氧化物等,雾霾现象就是一种典型的总悬浮颗粒物污染[5-6].现假设某市区内有三个排放总悬浮颗粒物(Total Suspended Particulate 简称TSP)的点源,其中一个是水泥厂,另两个是燃煤发电厂.水泥厂每生产1 t水泥排放86 kg总悬浮颗粒物,而发电厂每烧1 t煤排放98 kg总悬浮颗粒物.两个发电厂燃煤量分别为 500 000 t/a和400 000 t/a,水泥厂燃煤量为260 000 t/a.当前,这三个总悬浮颗粒物排放源都没有采用控制措施.现在,每个点源可以选择的控制方法的去除效率和费用如下表所示.此问题的目标是以最小的费用把水泥厂和两个发电厂的总悬浮颗粒物总排放量削减80%.
注:y/t表示元/吨,t/a表示吨/年,kg/a表示千克/年,kg/t表示千克/吨.
2 符号及参数说明
2.1 符号说明
i—污染源,1表示发电厂1,2表示发电厂2,3表示水泥厂;
j—控制方法,0表示不控制,1表示斜板沉淀槽,2表示多级除尘器,3表示长锥除尘器,4表示喷雾洗涤器,5表示静电除尘器;
Xij—点源i采用控制方法j的生产量;
M—未控制前小区TSP总排放量;
Mp—小区TSP的总允许排放量;
Mi—未控制前第i个点源TSP的排放量;
Mpi—控制后第i个点源TSP的排放量;
Ej—采用第j种控制方法后TSP的去除效率;
Z—采用各种控制方法后的总费用.
2.2 参数说明
2.2.1 总排放量(M)
小区内排放总悬浮颗粒物的点源共有三处,即发电厂1、发电厂2和水泥厂,故总排放量为各点源排放量之和,
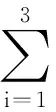
2.2.2 允许排放量(Mp)
允许排放量指在采取了一定的控制方法后,最大允许排放污染物的数量,本文要求将总悬浮颗粒物总排放量削减80%,即允许排放20%,故
Mp=M×20%=87 750 000×0.2=17 550 000(kg/a)
采取不同的控制方法后,悬浮颗粒物的去除效率不同,导致最终的排放量不一样.故采取控制后点源i的总悬浮颗粒物排放量为
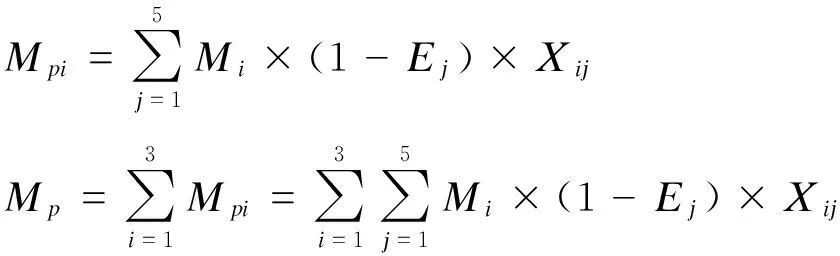
3 建立数学模型并求解
3.1 数学模型
在对大气污染进行控制的过程中,一方面我们要降低成本,以最少的费用完成任务;另一方面我们还要选择合理的控制方法将污染物控制在允许的范围内,使污染物的削减量达到国家允许的范围.就成本而言,我们应选择费用最低的控制方法,如斜板沉淀槽去污法,而为了增大削减量又应该选择去污效率较高的控制方法如静电除尘去污法,它的去污效率可达97%.但通过比较不难发现,费用低的控制法往往去污效率低,去污效率高的控制法,费用相对较高.如何平衡这一对矛盾体,在保证削减量的同时使所需费用最低,成为问题的关键和难点.通过目标和条件的综合考量,可将该问题归结为最优化问题,并建立了如下最优化数学模型:
s.t.
minZ=1.0X11+2.0X14+2.8X15+1.4X21+2.2X24+3.0X25+1.1X31+1.2X32+1.5X33+3.0X34
(1)
X10+X11+X14+X15=500 000
(2)
X20+X21+X24+X25=400 000
(3)
X30+X31+X32+X33+X34=260 000
(4)
98X10+39.0X11+5.7X14+2.9X15+98X20+39.0X21+5.7X24+2.9X25+86X30+34.9X31+
22.1X32+13.6X33+5.1X34≤17 550 000
(5)
在上述模型中,(1)为目标函数,保证了采取各种控制TSP排放量的方法后,所需费用最小;(2)、(3)、(4)式为限制条件,要求发电厂1的燃煤量为500 000 t/a,发电厂2的燃煤量为400 000 t/a,水泥厂的燃煤量为260 000 t/a,符合题目要求;(5)式保证了采取控制措施后TSP的总排放量削减80%,即不超过17 550 000 kg/a.
3.2 LINGO求解
为更加快捷准确地得到模型结论,经分析建立如下LINGO求解程序:
sets:
polution/elec1,elec2,cement/:coal,discharge;
controls/con0..con5/:effect;
arcs(polution,controls):production,fare,include;
endsets
data:
coal=500000,400000,260000;
discharge=98,98,86;
effect=0,0.59,0.74,0.84,0.94,0.97;fare=0 1.00 0 0 2.00 2.80
0 1.40 0 0 2.20 3.00
0 1.00 1.20 1.50 3.00 0;
enddata
min=@sum(arcs(i,j):fare(i,j)*production(i,j)*include(i,j));@sum(polution(i):@sum(controls(J):discharge(I)*(1-effect(j))*production(i,j)*include(i,j)))<=@sum(polution(i):coal(i)*discharge(i))*0.2;
@for(polution(i):@sum(controls(j):production(i,j)*include(i,j))=coal(i));
@for(arcs(i,j):include(i,j)=@if(fare(i,j)#eq# 0,0,1));
@for(arcs:@gin(production));
运行程序,整理后结果如表2所示:

表2 最小费用及各点源采用不同控制方法的生产量
4 控制方案的分析与评价
结果数据表明,在发电厂1采用斜板沉淀槽和喷雾洗涤器的控制方法每年分别燃煤320 886吨和179 114吨,在发电厂2采用喷雾洗涤器的控制方法每年燃煤400 000吨,在水泥厂采用多级除尘器的控制方法每年燃煤260 000吨既可以最小的费用1 871 114元/年使水泥厂和两个发电厂总悬浮颗粒物的总排放量不超过17 550 000 kg/a.各项数据清晰可靠,均符合题目要求,且操作方便、易行,值得推广.
5 结语
近年来,随着人们对生存环境的高度重视,特别是雾霾现象对人们正常出行和身体健康造成的危害,大气污染和防治的研究逐步趋于白热化,国家和政府也出台了一系列相应的法律政策[7-9],但对大气污染控制的各项指标量化分析的研究却是该领域的一个薄弱点.控制方法的选择、污染物的控制效果以及相应污染物的削减费用是大气污染防治最重要的指标和信息.本文从实际问题出发,给出的数据真实可靠,且通过详细分析研究,建立了最优化数学模型,同时解决了这三方面的问题,并用LINGO软件求解该优化问题,执行效率高,速度快,结果精确. 总之,上述大气污染物治理模型为国家和政府制定更加有效、经济的污染物控制和削减方案提供了科学的依据,具有一定的参考价值和指导意义.
[1] 刘正广,马忠玉,刘婷婷.近20年来中国工业主要污染物的时空分布特征分析[J].环境污染与防治,2010,32(3):185-188.
[2] 何吉成.30年来中国民航运输行业的大气污染物排放[J].环境科学,2012,(01):1-7.
[3] 史宇,罗海江,林兰钰,等.如何从规划层面推进城市大气污染防治——以北京市为例[J].干旱区资源与环境,2017,(05):64-69.
[4] http://baike.so.com/doc/3831091-4022940.html
[5] 丁宏.治理雾霾与防治大气污染[J].资源节约与环保,2015,(12):137.
[6] 齐婧辰.雾霾天气对人体健康的影响[J].中国城乡企业卫生,2017,(03):43-47.
[7] 王德征,江国虹,顾清,等.采用时间序列泊松回归分析天津市大气污染物对心脑血管疾病死亡的急性影响[J].中国循环杂志,2014,(06):453-457.
[8] 毛雪莲,李冬,朱晓华.环境污染对人体健康的影响及对策研究进展[J].环境与可持续发展,2016,(06):127-129.
[9] 陈青祥.我国大气污染防治法律制度研究[D].太原:山西财经大学,2015.
[10] 陈华友,等.数学模型与数学建模[M].北京:科学出版社,2014.
(责任编辑郑绥乾)
StudyonOptimalControlofAirPollutionEmissions
XU Qin
(GansuUniversityofChineseWedicine,Dingxi743000,China)
In view of the problems of air pollution seriously affecting human health,enumerating examples,the optimization mathematical model is established by quantitative analysis,the LINGO method can be used to calculate the pollutant reduction of 1 871 114 yuan/year by adopting different control methods,such as inclined plate settling tank,spray scrubber,multi-stage dust collector,etc.,which can be used in different pollution sources.The results show that the optimization algorithm with high efficiency,fast,accurate,and can be the most effective way to control,the lowest cost to the total emissions of air pollutants reduction to the national standards,provides a scientific basis for the control of pollutants and to develop more effective and economic for the relevant departments and cuts,has a certain the reference value and guiding significance.
total suspended particulate matter;reduction degree;control method;allowable emission
O 221.1
A
1000-5846(2017)04-0310-05
2017-04-28
定西师范高等专科学校一般项目(TD2016YB10);定西师范高等专科学校一般项目(TD2016YB09)
徐芹(1980-),女,甘肃武威,甘肃中医药大学定西校区理科教学部,讲师,硕士研究生,从事最优化理论及其应用研究.
——专业服务大型水泥厂

