一种改进的三维网格凸度衡量方法

李 瑞,刘 磊,盛 蕴,张桂戌

(华东师范大学 计算机科学与软件工程学院,上海 200062)

一种改进的三维网格凸度衡量方法

李 瑞,刘 磊,盛 蕴,张桂戌

(华东师范大学 计算机科学与软件工程学院,上海 200062)

针对现有方法需要不断地调整投影方向、时间消耗大的缺点,提出了一种改进的三维网格凸度衡量方法,该方法只需在物体主方向投影一次,减少了时间消耗.该方法首先采用主成分分析(Principal Component Analysis,PCA)计算网格模型的主方向,然后计算模型在主方向上的投影面积和网格模型中每个面片在主方向上的投影面积之和,将它们的比值作为凸度值的初始估计,最后在主方向上对模型进行切片处理,计算所有切片的二维凸度值的加权平均,并将其作为凸度值的修正.实验结果证明,这种改进的凸度衡量方法在计算速度上比现有方法更快,而且更加符合人类的视觉感知.

形状分析; 凸度衡量; 主成分分析

0 引 言

形状分析是计算机视觉、模式识别和计算机图形学中的基础性问题.形状的几何特征提取是形状分析的一个子方向,常用的几何特征有凸度[1-2]、线性度[3-5]、紧密度[6]、椭圆度[7]和对称度[8]等.其中,凸度在形状分解[9]、分类[10]和检索[11-12]等领域得到了广泛的研究,在人类的视觉感知中扮演着重要角色[13-14].凸的物体具有显著的视觉特征和简单的几何特性[13,15],所以基于视觉显著性的模型分解往往把模型的凸度值作为分解的依据[9,16-18],这种基于凸度值的分解比单纯的基于严格凸模型的分解具有更好的鲁棒性,而且可以把凸度值设为分解的阈值,控制分解的细致程度[9].

在三维空间中,只有当网格模型内任意两点之间的连线都在这个模型的内部时,这个模型才是一个完全凸的模型.一般来说,三维网格模型的凸度衡量方法需要满足以下4个基本条件[1,19].

(1)任意网格模型的凸度值都是一个实数,并且在0到1之间.

(2)只有当网格模型是完全凸的时候,其凸度值才为1.

(3)一定存在这样的网格模型,它的凸度值无限接近于0.

(4)凸度衡量方法对于给定的网格模型必须满足相似变换不变性.

1 相关工作

本文将回顾几种常用的二维和三维凸度衡量方法.为了能区别二维和三维的凸度衡量方法,我们用小写字母c表示二维凸度衡量方法,用大写字母C表示三维凸度衡量方法.

1.1 二维形状的凸度衡量方法

二维凸度的衡量方法已经得到了广泛的研究,其中最常用的是将形状本身的面积与其凸包的面积的比值作为凸度值[1].

定义1 给定一个二维形状s,其凸包为CH(s),则它的凸度c1(s)为

公式(1)中,c1是一种简单而高效的衡量方法,具有较强的抗噪性,但它对边界的变化不敏感,比如对细长的凹陷反映不敏感[1].基于周长的凸度衡量方法解决了这个问题.在基于周长的凸度衡量方法中,对于任意一个二维形状s,它的周长和凸包的周长一定存在着

这样的关系,当s为完全凸的时候,公式(2)两边才相等.因此,s的凸包周长与其本身周长的比值可用作凸度值的衡量.

定义2 给定一个二维形状s,其凸包表示为CH(s),则它的凸度c2(s)为

因为c2是一种基于周长的凸度衡量方法,它对边界的变化较为敏感,所以抗噪性比c1要差.

还有一些与凸包无关的凸度衡量方法,如ˇZuni´c等人[1]提出了一种基于边界投影的方法,这种方法需要不断旋转图形来寻找一个使凸度值最小的外接矩形;Rosin等人[20]提出了一种具有对称性的凸度衡量方法,与基于凸包的方法不同,这种方法通过一个凸多边形去逼近原始多边形,以这个凸多边形与原多边形的面积的比值作为凸度值;在此方法的基础上,Kolensnikov等人[21]提出了一种基于动态规划的优化算法来计算最优拟合多边形;Rahtu等人[22]提出了一种基于概率的凸度衡量方法,这种方法通过计算图形内任意两点连线上的某一点属于图形内部的概率来计算凸度.

1.2 三维网格的凸度衡量方法

相比于二维凸度衡量方法,三维网格的凸度衡量方法并没有得到广泛的研究.一些二维的凸度衡量方法可直接扩展到三维空间,与定义1中的二维凸度衡量方法类似,一种常用的基于体积的三维网格凸度衡量方法为网格自身体积与其凸包的体积之比.

定义3 给定一个三维网格M,其凸包为CH(M),则它的凸度C1(M)为

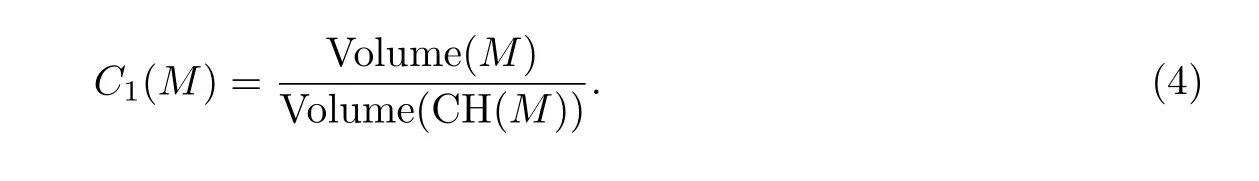
值得注意的是,本文所提及的三维网格都是三维封闭网格.与c1类似,C1同样对于细长的凹陷不敏感[2],而且对于具有相同体积和凸包体积的网格模型,根据C1的计算方法会得到相同的凸度值,而这在很多情况下是不合理的,如图1所示.

而一些二维的凸度衡量方法不能直接扩展到三维空间,如果我们把基于边界的二维凸度衡量方法c2直接扩展到三维空间,则二维空间中形状的边界可以看作是三维空间中网格的表面积.在二维空间中,一定存在不等式(2),但在三维空间中,却不存在关于网格模型表面积与其凸包的表面积的不等式.这是因为对于一些类似于图2的网格模型,存在

不等关系;而对于一些类似于中空立方体的网络模型(见图8),却存在相反的不等关系

因此,不能直接将二维的c2扩展到三维空间.

图1 具有相同的体积与凸包体积的网格模型Fig.1 Different meshes with identical mesh and convex hull volumes

图2 一个具有很多空洞的立方体模型Fig.2 A cube with many holes

为了解决方法C1对细长凹陷不敏感的问题,Lian等人[2]提出了一种基于投影的三维网格凸度衡量方法,该方法是由文献[1]扩展而来.

定义4 给定一个三维网格模型M,它的凸度值可以定义为

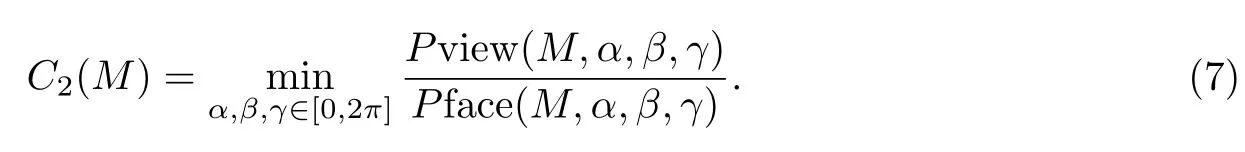
公式(7)中,Pface(M,α,β,γ)和Pview(M,α,β,γ)是网格模型分别绕x,y和z轴旋转α,β和γ角度后的Pface和Pview,其中,Pface是网格上所有面片分别在坐标平面XOY,Y OZ和ZOX上的投影面积之和,即

Pview是网格模型在平行于坐标平面的外包立方体上的投影面积之和,因为外包立方体有6个面,所以Pview可以表示为

图3(a)表示网格模型中的一个三角面片在坐标平面上的投影.图3(b)表示网格模型在三个坐标平面的投影,即Pviewx,Pviewy和Pviewz.对于所有的网格模型都存在不等关系

只有当网格模型为完全凸的时候等号才成立.而不断的旋转模型,是为了找到一个最小的凸度值作为模型最终的凸度值.

由于最小化C2(M)的计算是一个非线性的优化问题,传统的优化方法不能解决,因此Lian提出了用遗传算法进行求解.在计算Pview时,需要将网格模型在3个坐标平面上进行透视投影,然后提取出缓冲区中的投影图,借此来估算投影面积.而遗传算法需要多次迭代,每次迭代又需要多次计算每个个体的值,导致该方法运行耗时,不方便使用,因此需要设计一种快速的凸度衡量方法.

基于以上问题,本文提出了一种改进的三维网格模型的凸度衡量方法.该方法同样是一种基于投影的方法,是对Lian的方法的一种改进.Lian的方法计算速度过慢的原因在于遗传算法需要多次计算投影面积,而本文的思想是只在特定方向上投影一次,再对在此方向上计算的投影比值进行修正,以最后的修正值作为网格的凸度值.因为这种新方法结合了基于体积的方法和基于表面积的方法,因此其具有基于体积的方法的抗噪性,又能对细长的凹陷较为敏感,而且相对于C2,新方法大大缩短了计算时间.

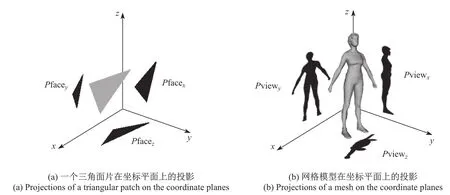
图3 Pface与Pview的示意图Fig.3 Illustration of Pface and Pview

2 改进的三维网格模型的凸度衡量

本文提出了一种改进的三维模型凸度衡量方法,通过旋转模型至某一固定方向,并对3个坐标平面进行投影来估计凸度的初始值;然后平行于每个坐标平面方向对模型进行切片,通过计算切片的凸度值对初始估值进行修正,从而得到最终的凸度值.该方法用公式表达为

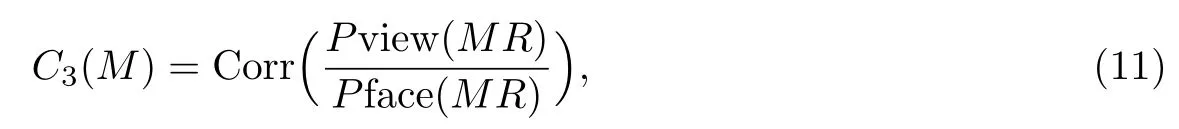
其中,R是将网格旋转至特定方向的旋转矩阵,Corr()是对初始估值的修正函数.

2.1 主方向上的初始估值

如上所述,我们希望通过旋转矩阵R把网格模型旋转至某一特定方向,通过这一方式来替代Lian的方法中耗时的遗传算法.从定义4可知,通过旋转模型至某一个特定方向,C2最终会达到一个最小值.一般来说,只有当模型的所有面片在三个坐标平面投影具有最大重合时,C2才会达到最小值.因此,我们的目标就是不通过优化算法,只旋转一次就让投影重叠的面积接近于最大值.

这里我们采用了主成分分析(PCA)来对旋转方向进行估计,这主要是基于以下两点原因.首先,PCA是一种常用的降维方法,通过对数据集协方差矩阵进行特征分解,得到数据集的主方向及其权值,数据集在主方向上具有最大的方差.因此PCA可以保证面片在坐标平面上的投影具有相对较大的重叠面积,从而获得一个相对较小的初始估值.其次,在接下来的修正过程中,垂直于主方向对模型进行切片比其他方向更能表示出模型的几何特征.

假设E为网格顶点的特征向量所组成的协方差矩阵,把公式(11)中的参数R用E代替,则在主方向上的凸度的初始估值Ce可以表示为

图4显示了4个三维网格模型的主方向,以及模型在坐标平面上的投影.从图中可以看出,初始估值Ce(M)与经过遗传算法优化后的值C2(M)比较接近.

图4 模型在主方向坐标系下的投影以及C2和Ce的值Fig.4 Mesh silhouettes along the principal axes with the mesh convexity values calculated by C2and Ce

但在主方向上的估计也有一定的局限性.在Pview与Pface比值最小的方向上,网格表面投影重叠最多,而主方向只能反映网格顶点在此方向上的方差最大.对于不是完全凸的网格,在主方向上可能没有投影重叠的表面,即在主方向上比值为1.如图5所示,图中的网格是一个工程部件的模型,可以计算出在主方向上的投影面积比为1,但是它并不是完全凸的.通过以上的例子可以看出,若直接用主方向上的比值代替最小比值作为网格的凸度值,不能满足凸度衡量方法的条件2,因此需要对主方向上的初始估值进行修正.

图5 一个用PCA会产生错误估计的模型Fig.5 An example whose convexity is overestimated by PCA

2.2 初始估值的修正

缺少合理高效的三维网格凸度衡量方法的一个重要原因是三维模型比二维形状的复杂度高.若能将三维网格的凸度问题转化为二维形状的凸度问题,那么借助于常用的二维凸度衡量方法,三维网格的凸度也能方便的计算出来.在二维凸度计算中,c1和c2是最基本的凸度衡量方法,我们把模型沿着主方向坐标轴进行切片,通过对切片进行二维凸度值测量来对初始估值进行修正.

类似于医学上断层扫描的思想,我们也可以在三个方向对网格模型进行“切片”.如图6所示,图中只显示了沿一个方向的切片,此方向上的切片都是凸的,但是在另外两个正交方向上存在凹切片.通过切片处理,一个网格模型被转换为一系列的二维形状,而这些二维形状的凸度则反映了原始网格的凸度值.因此,我们使用这些二维形状的凸度值来计算每个主方向的修正系数.

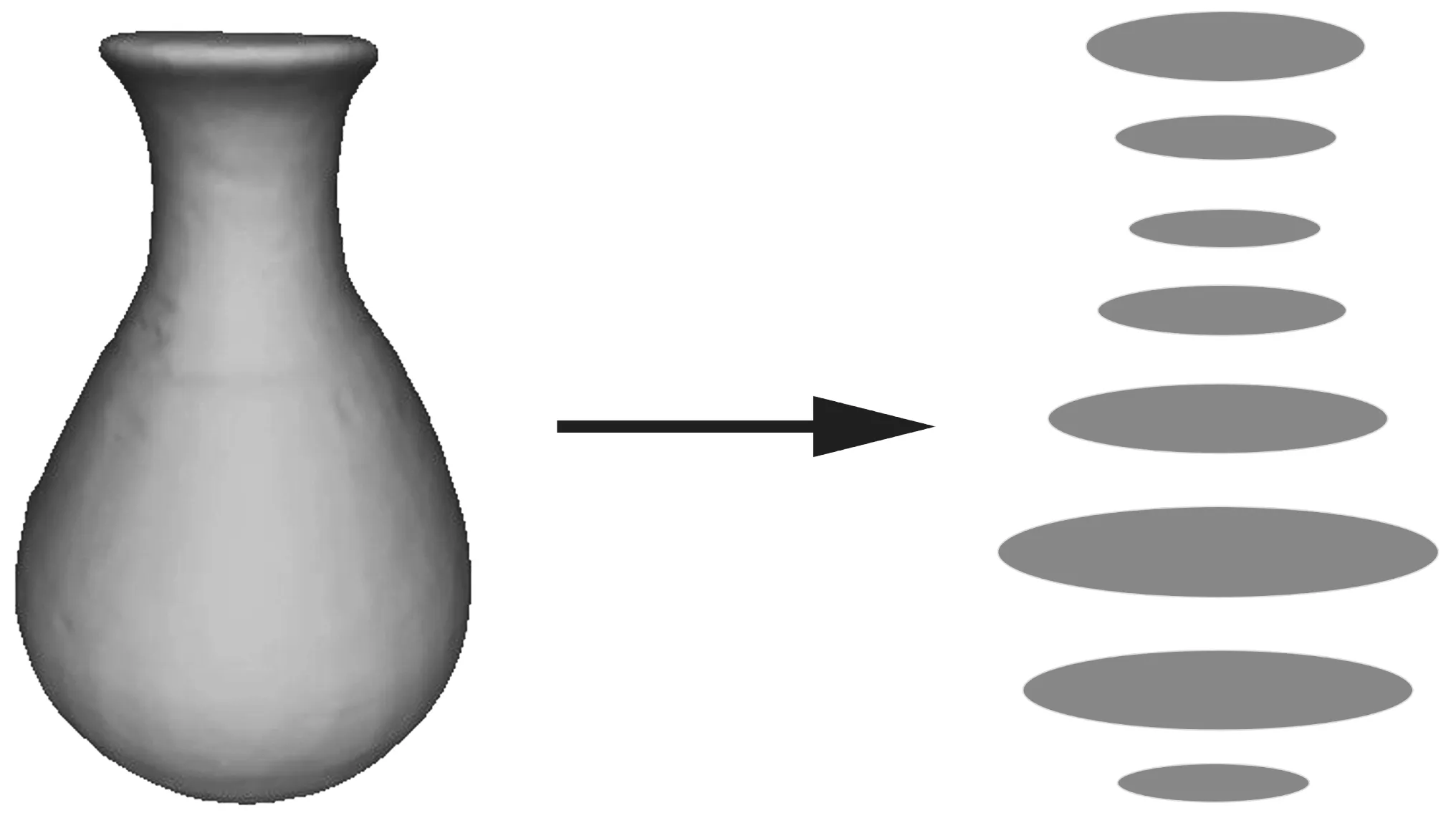
图6 三维网格切片示意图Fig.6 An illustration of mesh slicing

本文通过计算切平面与网格的交点得到切片,由于网格模型的表面一般凹凸不平,如图7所示,以上方法所得切片的边界常呈锯齿状,而基于边界的方法c2对边界的变化非常敏感,若采用c2进行凸度计算,则会产生较大误差.因此我们采用基于面积的方法c1来消除边界噪声产生的影响.

图7 三维网格表面Fig.7 The surface of 3d mesh

假设我们在某一方向上把三维网格模型切成N+1份,每个切片之间是等距的,则修正系数可以表示为

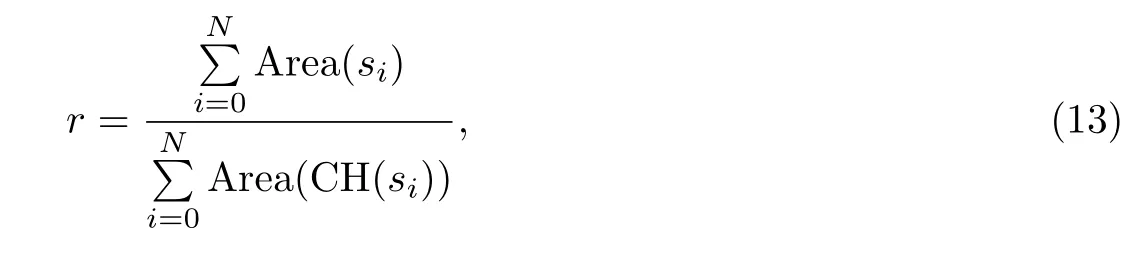
其中,Area(si)是第i个切片的面积,Area(CH(si))是第i个切片对应的凸包的面积.实际上,计算Area(si)是比较复杂的,通过改变公式(13),将其分子分母同时乘以切片的间距lstep,则可变为

在N足够大的时候,分子可约等于模型的体积.

为了使切片数量根据网格模型的精度自适应调整,保留更多的几何特征,我们提出平均网格边长的概念.网格模型中所有边长的平均值即为平均网格边长l,我们把平均网格边长的一半作为切片的步长,即

假设模型在某一主方向上最大的投影长度为L,那么总的切片数量为N=L/lstep.为了控制切片数量,我们设置了一个最大阈值Nmax,当N等于或超过这个阈值时,则用最大阈值作为切片数量,即

针对本文中用到的模型,我们将Nmax默认设置为200.如果Nmax设置的较小,则会影响凸度计算的精度,如果Nmax设置的较大,则会增加凸度的计算时间,综上,三个方向的修正项最终可以表示为

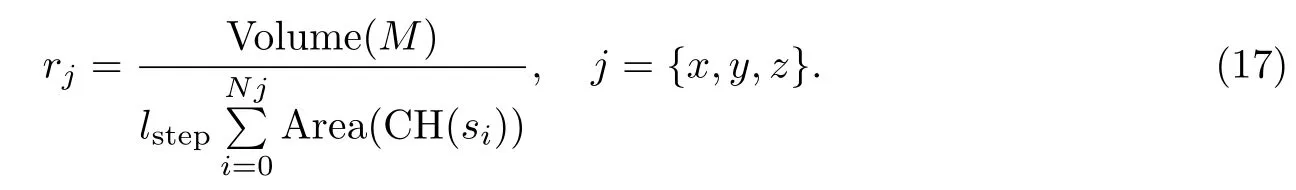
定义5 对于一个给定的三维网格M,它的凸度值C3(M)为

其中,

为了证明C3的可行性,我们需要验证它是否满足凸度衡量方法的4个基本条件.

证 明:如果网格模型M是完全凸的,则每一个二维的切片都是凸的,那么rx=ry=rz=1.另一方面,在任意方向上Pview(ME)=Pface(ME),所以C3(M)=1恒成立,条件2得证.当M不是完全凸的时候,必定存在某些切片是非凸的,则rx,ry,rz∈(0,1],而任意一个模型在主方向上Pview≤Pface一定成立,根据公式(18)和公式(19),我们可以得出C3(M)≤1,条件1得证.由于主方向的计算与网格初始的状态和网格的位置无关,而修正项是在主方向的基础上进行的计算,因此最后计算出的凸度值具有平移旋转不变性.又因C3(M)是基于比值的计算,因此具有缩放不变性,条件4得证.

为了证明条件3,我们构造出一个中空的立方体,如图8所示.假设立方体的外边长为a,内边长为b,则

当不断增大b,使其无限接近于a时,

条件3得证.至此,我们已经证明了定义C3满足凸度衡量的基本条件.

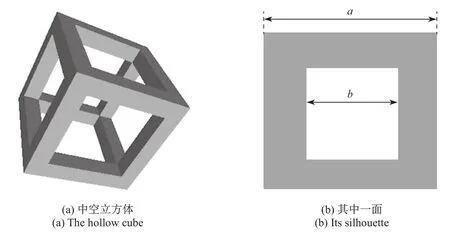
图8 中空立方体Fig.8 The hollow cube

此外,如果采用Lian的方法计算中空立方体的凸度,则

如果不断减少b,直到b=0,则C2(M)=1;而如果不断增加b,使其无限接近于a,由C2计算的凸度值为

本文认为这是一种不合理的情况.

3 实验结果对比与分析

本节我们对一些来自公共数据库里的模型进行定量分析.第3.1节与其他三维网格凸度衡量方法进行对比;第3.2节与Lian的方法进行计算时间的对比.

3.1 实验分析

为了证明本文方法的有效性,我们采用McGill Articulated 3D Shape Benchmark和Princeton Benchmark[23]数据库中的网格模型进行实验.在实验之前,我们先对网格模型进行预处理,将网格模型的重心设为坐标系原点.

图9 不同凸度衡量方法的对比Fig.9 The comparison of different convexity measures

图9显示的是用不同凸度衡量方法计算出的凸度值,网格模型按照C3的值进行排序.通过结果可以看出,本文方法对模型1,3,6,7和8计算的凸度值较低,相反,C2的值较大.从模型18我们可以看出,单纯基于体积的方法C1对于细长的凹陷并不敏感,而C2和C3却能够给出合理的结果.由于公式(14)是一个近似计算,对于球形模型会产生一个较大的误差,所以模型23计算出的值并不是完全凸的.

为了更好的表明C2与C3的区别,我们人为设计了4个模型,如图10所示,当内边界b分别等于0,0.2a,0.5a和0.8a时,C2与C3的凸度值不断地减少,这符合我们的视觉感知.

图11显示的是一个具有较深凹槽的立方体,当凹槽的宽度n趋近于0的时候,凹槽的体积趋近于0,则此时C1(M)为

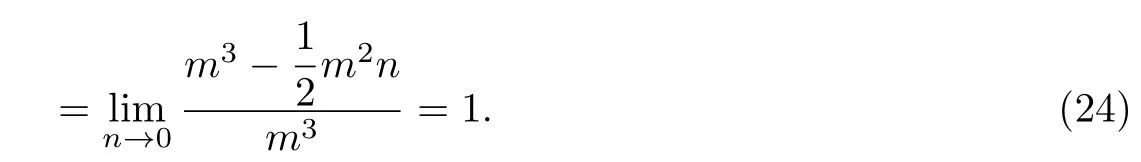
图10 不断增大b时的凸度值Fig.10 The hollow cubes with broadening b

图11 一个具有深凹的立方体模型Fig.11 A cube with a deep dent

然而这个值不能反映出凹槽的存在,而C3却可以探测到这个凹槽的存在,

对于图1的两个模型,C3计算出的凸度值分别为0.6756和0.7483,即凹陷深的模型,凸度值较低.而C1只受到凹陷的体积的影响,没有考虑到凹陷是在模型的边缘区域还是内部区域.

图12显示的是同一手模型在不同姿势下的凸度.从图中可以看出,5个手指完全张开时,凸度值最大.而当手指弯曲的程度越高或弯曲手指越多时,其凸度值越小,这与人们心理上对凸度的衡量是一致的.

图12 不同手势的凸度值Fig.12 Hand gestures calculated by C3

本文从MPI-FAUST、McGill Articulated 3D Shape Benchmark和Princeton Benchmark数据库中提取了80个网格模型,共分为5个类别,图13显示的是其中的一些样本.我们把模型的凸度作为特征进行了分类实验,实验采用的k近邻分类算法,由于样本集较小,我们采用了留一法交叉验证(Leave-one-out Cross Validation).当采用C2作为特征进行分类时,分类的准确率为81.25%,而当采用C3作为特征进行分类时,分类的准确率提升到了85.00%.由于此处采用的是单一全局特征作为分类的特征,不能达到较高的分类准确率,当把C2和C3作为特征进行分类时,分类的准确率达到了92.50%.

图13 5类模型的样本Fig.13 Samples of 5 types of meshes

3.2 算法的时间复杂度分析

Lian在算法中使用的参数为50个个体,进行200次迭代.当网格模型的顶点非常多的时候,此算法的执行速度较慢.与Lian的方法不同,本文的方法避免使用遗传算法多次从帧缓存中读取图像,而只需计算一次投影面积.表1显示了在计算网格模型的凸度时,本文方法与Lian的方法在时间消耗上的对比.本文使用的实验环境是:CPU为Intel CORE i5;内存为6GB;编程环境为 Microsoft Visual Studio 2010.Lian的方法时耗的计算以从缓冲区读取图像的时间为基准,再将此时间乘以迭代次数得到运行总时间(实际运行时间比表中显示的时间更长).从表中可以看出,本文方法与Lian的方法相比,大大减少了时耗.

4 结 论

为了解决现有三维网格模型凸度衡量方法的缺点,本文提出了一种根据Lian的方法C2进行改进的方法C3.与C1相比,C3可以探测到细长的凹陷,而且对于具有相同体积和相同凸包体积的模型,C3能够根据凹陷的深浅进行凸度计算,而不是单纯的计算体积比,这更加符合人类的视觉感知.与C2相比,C3通过引入基于面积的二维形状的凸度计算,使该方法具有了基于体积的方法与基于投影的方法的特点.通过先确定主方向再进行投影,C3极大的缩短了C2的计算时间,这使其更能适用于实际应用.

表 1 时间消耗对比Tab.1 Comparison of time consumptions

[1]ˇZUNI´C J,ROSIN P L.A new convexity measure for polygons[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2004,26(7):923-934.

[2] LIAN Z,GODIL A,ROSIN P L,et al.A new convexity measurement for 3D meshes[C]//Computer Vision and Pattern Recognition(CVPR),2012 IEEE Conference on.IEEE,2012:119-126.

[3]ˇZUNI´C J,ROSIN P L.A rectilinearity measurement for polygons[C]//European Conference on Computer Vision.Berlin:Springer,2002:746-758.

[4] LIAN Z,ROSIN P L,SUN X.Rectilinearity of 3D meshes[J].International Journal of Computer Vision,2010,89(2/3):130-151.

[5] ROSIN P L.A two-component rectilinearity measure[J].Computer Vision and Image Understanding,2008,109(2):176-185.

[6]ˇZUNI´C J,HIROTA K,MARTINEZ-ORTIZ C.Compactness measure for 3D shapes[C]//Informatics,Electronicsamp;Vision(ICIEV),2012 International Conference on.IEEE,2012:1180-1184.

[7] ROSIN P L.Measuring shape:Ellipticity,rectangularity,and triangularity[J].Machine Vision and Applications,2003,14(3):172-184.

[8] LEOU J J,TSAI W H.Automatic rotational symmetry determination for shape analysis[J].Pattern Recognition,1987,20(6):571-582.

[9] REN Z,YUAN J,LIU W.Minimum near-convex shape decomposition.[J].IEEE Transactions on Pattern Analysisamp;Machine Intelligence,2013,35(10):2546-2552.

[10] ROSIN P L.Classification of pathological shapes using convexity measures[J].Pattern Recognition Letters,2009,30(5):570-578.

[11] SARFRAZ M,RIDHA A.Content-based image retrieval using multiple shape descriptors[C]//Ieee/acs International Conference on Computer Systems and Applications.2007:730-737.

[12] YANG Y B,LIN H,ZHU Q.Content-based 3D model retrieval:A survey[J].Chinese Journal of Computers,2004,27(10):1297-1310.

[13] BIEDERMAN I.Recognition-by-components:A theory of human image understanding[J].Psychological Review,1987,94(2):115.

[14] SIDDIQI K,KIMIA B B.Parts of visual form:Computational aspects[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1995,17(3):239-251.

[15] SINGH M,HOFFMAN D D.13-part-based representations of visual shape and implications for visual cognition[J].Advances in Psychology,2001,130:401-459.

[16] LIU H,LIU W,LATECKI L J.Convex shape decomposition[C]//Computer Vision and Pattern Recognition(CVPR),2010 IEEE Conference on.IEEE,2010:97-104.

[17] GHOSH M,AMATO N M,LU Y,et al.Fast approximate convex decomposition using relative concavity[J].Computer-Aided Design,2013,45(2):494-504.

[18] ASAFI S,GOREN A,COHEN-OR D.Weak convex decomposition by lines-of-sight[J].Computer Graphics Forum,2013,32(5):23-31.

[19] 刘磊.三维网格特征提取与分割[D].上海:华东师范大学,2015.

[20]ROSIN P L,MUMFORD C L.A symmetric convexity measure[J].Computer Visionamp;Image Understanding,2004,103(2):101-111.

[21] KOLESNIKOV A,FRANTI P.Optimal algorithm for convexity measure calculation[C]//IEEE International Conference on Image Processing.2005:353-356.

[22] RAHTU E,SALO M,HEIKKILA J.A new convexity measure based on a probabilistic interpretation of images[J].IEEE Transactions on Pattern Analysisamp;Machine Intelligence,2006,28(9):1501-1512.

[23]CHEN X,GOLOVINSKIY A,FUNKHOUSER T.A benchmark for 3D mesh segmentation[J].ACM Transactions on Graphics,2009,28(3):341-352.

(责任编辑:李 艺)

An improved convexity measure for 3D meshes

LI Rui,LIU Lei,SHENG Yun,ZHANG Gui-xu
(School of Computer Science and Software Engineering,East China Normal University,Shanghai200062,China)

In this paper we proposed an improved 3D mesh convexity measure by projecting only once a given 3D mesh onto the orthogonal 2D planes along its principal directions.Unlike the previous work which was time-consuming and required constant adaptations of the projection direction,we used the calculated result along the principal directions as an initial estimate of mesh convexity,followed by a correction process.In the initial estimation,our measure computed only once the summed area ratio of mesh silhouette images to mesh faces,along the principal directions of the mesh.Then,the mesh was sliced into a number of 2D cross sections along its principal directions.Finally,a 2D convexity measure for the 2D sliced cross sections was employed to correct the convexity overestimated by the initial estimation.Experimental results had demonstrated the effectiveness and effciency of the improved convexity measure against the existing ones.

shape analysis;convexity measure;principal component analysis

TP391.4

A

10.3969/j.issn.1000-5641.2017.06.006

1000-5641(2017)06-0063-13

2016-08-16

国家自然科学基金(61202291)

李 瑞,男,硕士研究生,研究方向为计算机图形学.E-mail:15201802836@163.com.

盛 蕴,男,副教授,硕士生导师,研究方向为计算机图形学、计算机视觉等.

E-mail:ysheng@cs.ecnu.edu.cn.