一种面向GPS单频RTK的周跳探测算法

金星,王玲,黄文德

(1.湖南师范大学 物理与信息科学学院,湖南 长沙 410012; 2.国防科技大学 机电工程与自动化学院,湖南 长沙 410073)

一种面向GPS单频RTK的周跳探测算法

金星1,2,王玲1,黄文德2

(1.湖南师范大学 物理与信息科学学院,湖南 长沙 410012; 2.国防科技大学 机电工程与自动化学院,湖南 长沙 410073)

针对传统码-载波相位周跳探测方法应用于单频RTK时,存在的对小周跳不敏感、易受码观测噪声的影响等问题,本文提出一种多普勒观测值辅助的单频周跳探测方法。该方法将连续两个相邻历元多普勒观测值与载波相位差分观测值相结合,以构造实时周跳探测的多普勒-载波相位差分序列。然后应用假设检验方法,检测单频载波相位观测值是否存在周跳。实测数据分析表明:本文提出的方法能够准确探测单频载波相位观测数据中的小周跳,且该方法对周跳探测的灵敏度比传统码-相位差分序列方法更高,适用于单频RTK定位技术。

周跳探测;单频RTK;多普勒观测;差分序列;假设检验

0 引 言

目前,GNSS导航定位已经被广泛应用在各个领域,比如行人导航、汽车导航、测绘、精密农业等领域。虽然不同应用领域对导航定位精度的要求也不尽相同,但对高精度位置服务的需求却与日俱增。

在高精度定位领域应用比较广泛的RTK技术就是采用载波相位观测值来获取高精度定位。然而在GNSS接收机进行连续的载波相位测量过程中,由于某种原因会导致整周计数发生错误,就会使载波相位观测值较之正常值出现一个整数周的跳跃,但不足一周的部分仍然正常,该跳跃称为周跳。文献[1]指出引起周跳的主要原因有:1) 信号遮挡;2) 到达接收机处卫星信号的信噪比低;3) 接收机或者卫星故障;4) 接收机的运动。文献[2]指出使用低成本单频GPS接收机进行RTK定位时,周跳将会更加频繁的发生。

在模糊度解算过程中,针对周跳的处理策略可以分为三类: 1) 单历元模糊度解算; 2) 当出现周跳时,对模糊度进行初始化; 3) 只在模糊度解算开始时,进行初始化,当出现周跳时,进行修复。第一类周跳处理策略,可以避免繁琐的周跳探测与修复算法,然而单历元模糊度解算需要高精度的伪距观测值,且在Kalman滤波中没有考虑模糊度观测值作为常量的特性,又由于伪距观测值精度通常比较低,因此,GPS单频RTK不适合采用该策略处理周跳。基于上述原因,在GPS单频RTK定位中,只有成功、可靠的探测周跳才能更好的进行周跳修复,才能避免模糊度参数频繁初始化,加快模糊度的收敛速度。目前双频观测值的周跳探测的方法很多:文献[3]和[4]利用P码伪距和双频的载波相位的组合构造MW和LG组合观测量来探测周跳,该方法的实质是利用电离层延迟在历元间变化缓慢的特性,具有较高的周跳探测精度[5-7]。然而,单频周跳探测仍然是一个开放性的问题,特别是对于动态导航定位。

1 单频RTK观测值噪声特性分析

周跳探测灵敏度一般会受到观测噪声的影响,在电离层不活跃时,码-相位组合法的观测噪声主要来源于伪距观测值,针对较小周跳探测时,探测结果往往会失败,主要是由于小的周跳会淹没在伪距噪声中。同样的,采用新方法时也需要对观测噪声特性进行分析。

在t时刻,GPS的伪距、载波相位和多普勒的观测方程分别为

Pi(t)=ρ(t)+c(dt(t)-dT(t))+Ii(t)+

T(t)+εPi(t)，

(1)

φi(t)=ρ(t)+c(dt(t)-dT(t))-Ii(t)+

λi·N(t)+T(t)+εφi(t)，

(2)

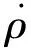
(3)

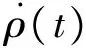
通常,在某一历元的观测量噪声可以用零均值白噪声表示,因此假设:

εk～N(0,σk) ，

(4)

式中,σk表示观测量的噪声标准差。文献[8]和[9]指出伪距观测噪声方差在0.11 ～0.35 m2之间,载波相位观测噪声方差要远小于伪距观测噪声。由于多普勒观测值的精度主要受多路径与导航信号强度的影响,本文将利用文献[9]中简化随机模型给出信噪比法实时估计多普勒观测值的噪声。

(5)

式中:S0为参考信噪比;σ0为信噪比最大时的标准差;a为放大系数。在中国香港CORS网不同站点(HKKT、HKMW、HKNP、HKST、HKOH、HKPC等多个采用徕卡接收机的站点),获取50组观测数据,数据的采样时间为1 h,采样间隔为1 s,截止高度角设置10°。将每组多普勒观测值进行多项式拟合,获得其观测值误差标准差,并计算每组观测值对应信噪比的均值,其中部分观测值误差如图1所示。

图1 部分多普勒观测值误差

将50组观测数据进行数理统计,并给出模型参数σ0=0.022 37 m,a=16,S0=9 m.观测值误差标准差与其对应的信噪比均值如图2所示。

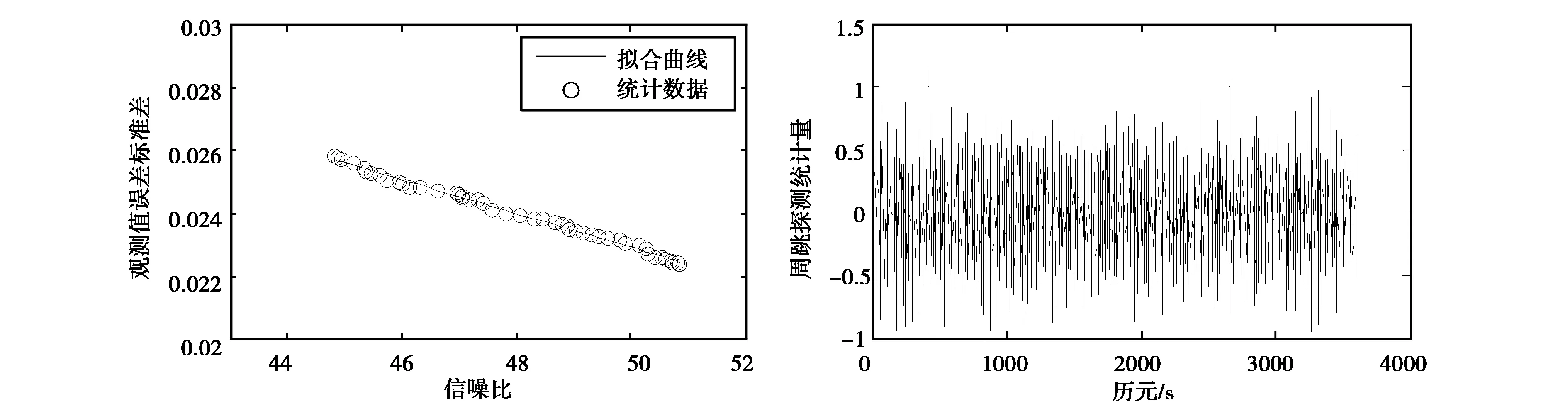
图2 多普勒观测值误差标准差与信噪比均值的关系 图3 传统码-相位差分序列周跳探测曲线

2 基于多普勒-载波相位差分序列的周跳探测方法

在电离层延迟变化比较平稳的地区,传统的单频码-相位组合方法的周跳探测性能主要取决于伪距观测噪声的大小,其探测曲线如图3所示。由于伪距观测值的精度比较差,一般会达到亚米级的精度,且GPS载波L1,L2的波长分别约为0.19 m和0.24 m,因此,使用该方法探测较小的周跳时(比如大小为1～2周的周跳),周跳一般会被淹没在观测量的噪声当中而无法及时探测。因此为了保证周跳探测的准确性,可以采用精度更高的多普勒观测值,并且预先对多普勒观测量的噪声水平做出估计。

2.1多普勒-载波相位差分序列的构造

在t-1和t连续两个相连历元,对式(3)求均值,对式(2)做差:

(6)

φi(t)-φi(t-1)=Δρ+cΔdt-cΔdT+

λi·ΔN-ΔIi+

ΔT+εφ，

(7)

(8)

则式(6)可以重新表示为

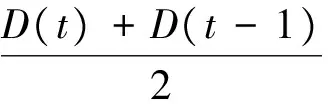
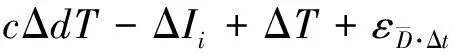
(9)

再对式(9)和式(7)做差,则:

Δγ(t,t-1)≡φi(t)-φi(t-1)-

(10)

2.2周跳探测的假设检验方法

当不存在周跳时,ΔN为零。则可以认为Δγ(t,t-1)服从零均值的正态分布:

(11)

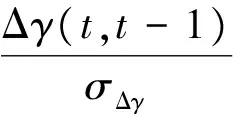
(12)

则η服从零均值的标准正态分布,周跳发生会使得η的均值不再为零。问题是根据样本值来判断η=0还是η≠0.为此,提出两个相互对立的假设

H0:η=η0=0和H1:η≠η0.

(13)

由式(13),Δγ(t,t-1)的方差σΔγ可以写作连续两个相邻历元之间的多普勒观测噪声方差的组合。由式(5),可以根据信噪比实时估计多普勒观测值噪声。

在实际应用中,用探测周跳效果来确定显著性水平,接着根据这一显著性水平来给出相应的拒绝域,并由拒绝域设定检测门限κ,如果η≥κ则可以判断此时存在周跳,否则判断此时没有产生周跳。

3 实验分析

3.1徕卡接收机静态数据验证分析

2017年5月使用徕卡接收机在长沙国防科大1号院北区19栋楼顶采集一组GPS观测数据,采样时间为1 h,采样间隔为1 s,截止高度角设置10°.

选取G03和G27 2颗在采样时间内未发生周跳的卫星进行分析,2颗卫星的信噪比如图4和图5所示。利用式(5)中的简化随机模型实时估计多普勒观测量的标准差,实时变化情况如图6和图7所示。

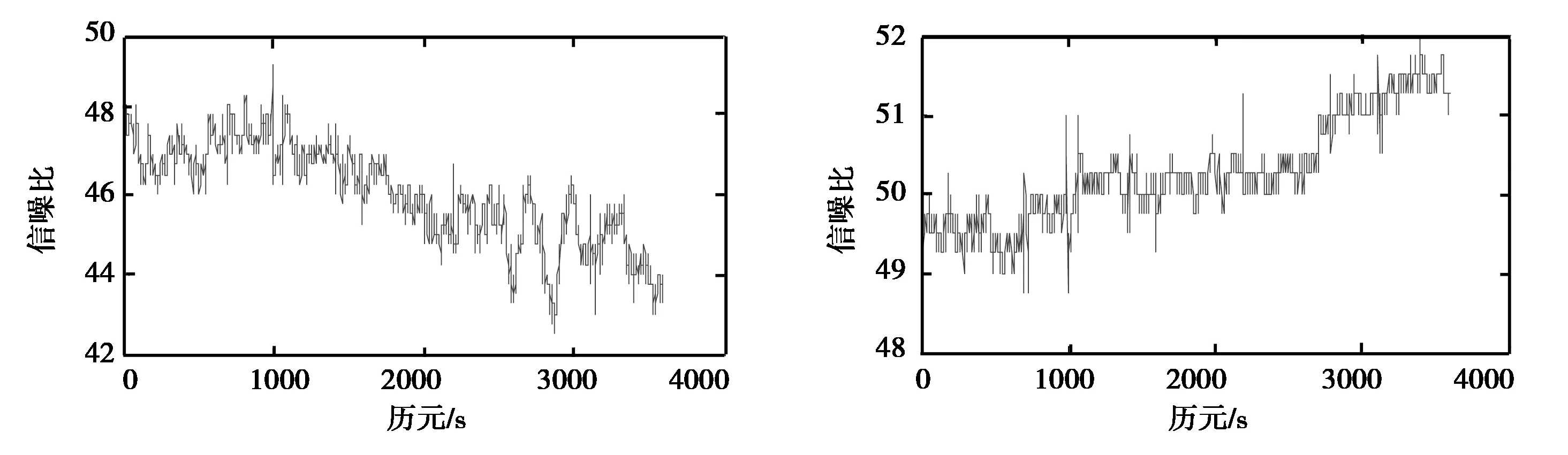
图4 G03信噪比变化情况 图5 G27信噪比变化情况

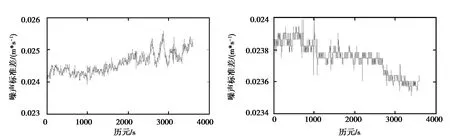
图6 G03的多普勒观测量噪声标准差 图7 G27的多普勒观测量噪声标准差

为了验证本文提出的新方法,人为的在某些历元的观测值上加入一些小周跳,并利用传统方法和本文提出的新方法分别进行探测。周跳探测方案如表1所示。

表1 周跳添加方案

利用传统的方法和本文提出的新方法探测周跳,对这2种方法的探测效果进行分析,假定探测成功率为99.9%,则此时假设检验的显著性水平为0.001,相应的检测门限是标准正太分布的上侧 0.001/2=0.000 5分位数,通过查阅正态分布表可以得到探测门限值为 3.31.两种方法探测周跳的结果如图8和图9所示。

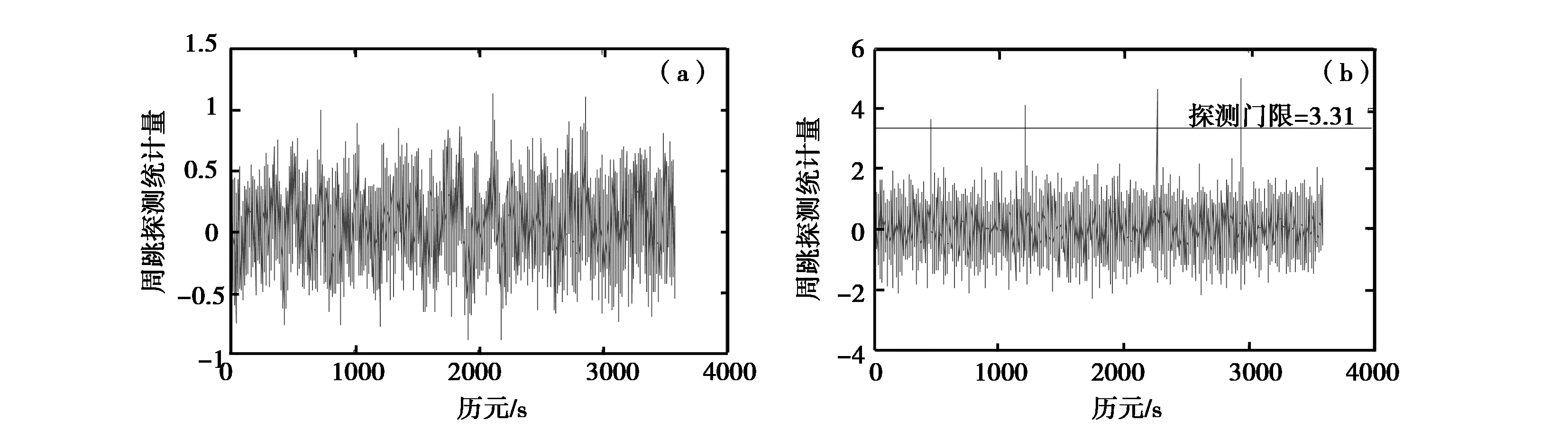
图8 G03周跳检测结果 (a)使用传统方法的周跳探测曲线; (b) 使用新方法的周跳探测曲线

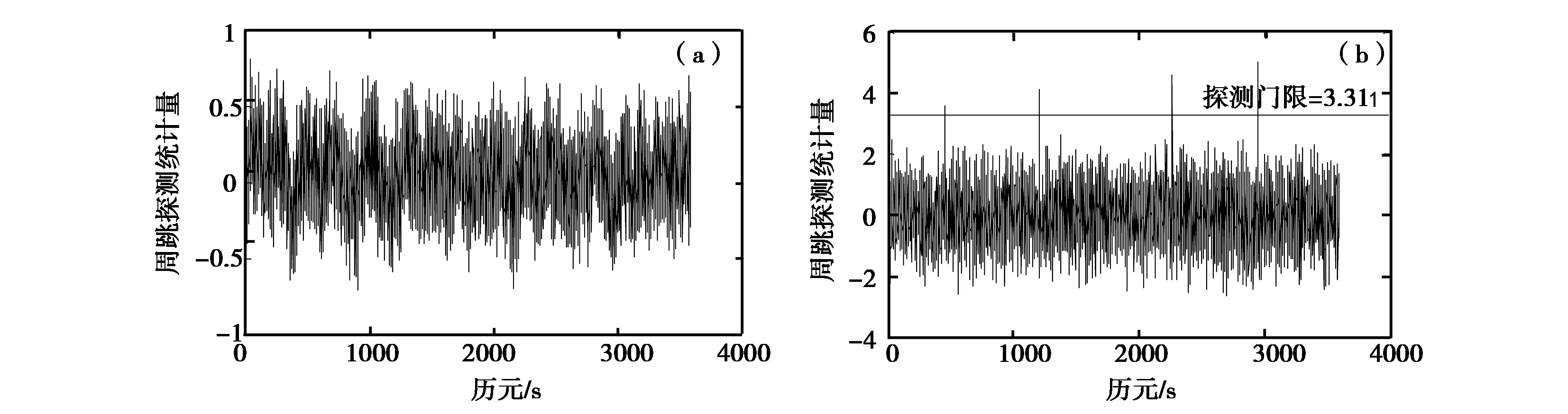
图9 G27周跳检测结果 (a) 使用传统方法的周跳探测曲线; (b) 使用新方法的周跳探测曲线

由表1可见,人为加入的周跳值都比较小,从图8和图9可见,对应于发生在相应历元上的小周跳,利用传统的方法周跳淹没在噪声中,而利用新的方法进行周跳检测时,检测曲线在发生周跳的时刻都超过了门限,这说明在发生小的周跳时改进的周跳探测方法可以做出正确的判断。

3.2U-blox接收机动态数据验证分析

此数据来源于2017年7月使用U-blox M8T接收机在长沙开福区采集。采样时间为30 min,采样间隔为1 s,截止高度角为15°,使用RTKLib程序进行转码获得。

选取卫星G03进行分析,该卫星的信噪比及实时估计多普勒观测量的标准差如图10和图11所示。

为了更好验证新的周跳探测算法的实用性,将实测数据进行周跳探测。两种算法的探测结果如图12所示。

图10 G03信噪比变化情况 图11 G03的多普勒观测量噪声标准差

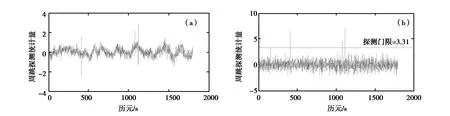
图12 G03周跳检测结果 (a) 使用传统方法的周跳探测曲线; (b) 使用新方法的周跳探测曲线

由图12可见,对于较大的周跳两种算法都可以有效探测,但是图12(a)中示出的探测结果在400历元左右时探测失败,图12(b)中示出新的周跳探测算法可以正确的进行探测。因此,相对于传统的方法而言,新的方法对于小周跳具有很好的探测效果,周跳探测新方法灵敏度比传统码-相位差分序列方法更高。

4 结束语

本文在传统的伪距与载波相位组合周跳探测的方法上做出了改进,利用多普勒观测量替换伪距观测量,提出了一种新的周跳探测方法。新的周跳探测方法对实时的多普勒观测噪声做出了估计,在一定程度上削弱了观测噪声对周跳探测的影响。实测数据验证表明:新的周跳探测方法相比于传统的伪距与载波相位组合周跳探测方法,提高了周跳探测的灵敏度,可以更为准确的发现较小的周跳。由于该方法只需要使用单频观测量,因此是一种面向GPS单频RTK的周跳探测算法。

致谢: 本课题由湖南省军民融合项目资助,同时感谢中国香港CORS网提供的相关实验数据。

[1] 李征航,张小红.卫星导航定位新技术及高精度数据处理方法[M]. 武汉:武汉大学出版社, 2013.

[2] REALINI, E. GoGPS free and constrained relative kinematic positioning with low cost receivers[D]. Politecnico Di Milano,2009.

[3] 方荣新,施闯,魏娜,等.GPS数据质量控制中实时周跳探测研究[J].武汉大学学报(信息科学版), 2009,34(9): 1094-1097.

[4] 王爱生,欧吉坤.无几何距离组合联合MW组合探测周跳的改进算法[J].数据采集与处理, 2007,22(4): 468-474.

[5] 熊伟,伍岳,孙振冰,等.多频数据组合在周跳探测和修复上的应用[J].武汉大学学报(信息科学版), 2007,32(4): 319-320.

[6] BISNATH S B.Efficient, automated cycle-slip correction of dual-frequency kinematic GPS date [C]//ION GPS-2000. Salt Lake City: Utah,2000.

[7] 刘柳,吕志伟,于晓东,等. GNSS周跳探测及产生周跳的影响因素研究[C]//第七届中国卫星导航学术年会论文集——S05 精密定位技术,2016.

[8] 高书亮,黄智刚,李锐.适用于单频GPS用户的周跳探测方法[J]. 北京航空航天大学学报, 2011,37(8): 1021-1025.

[9] 柳响林.精密GPS动态定位的质量控制与随机模型精化[D].武汉:武汉大学,2002.

ACycleSlipsDetectingAlgorithmforGPSSingleFrequencyRTK

JINXing1,2,WANGLing1,HUANGWende2

(1.CollegeofPhysicsandInformationScience,HunanNormalUniversity,Changsha410012,China;2.CollegeofMechanicalEngineeringandAutomation,NationalUniversityofDefenseTechnology,Changsha410073,China)

Aiming at the problem that the traditional code-carrier phase cycle detection method is applied to single frequency RTK, which is not sensitive to small cycle slips and is susceptible to observation noise, the thesis presents a single frequency cycle slip detection method with Doppler observations supporting. And this method combines two consecutive epochal Doppler observations with carrier phase difference observations to construct a Doppler-carrier phase difference sequence for real-time cycle slip detection. Then the hypothesis-test method is applied to detect whether there is a cycle slip in the single frequency carrier phase observations. Finally, the measured data shows that the method proposed in the thesis can accurately detect the small cycle slips in the single frequency carrier phase observation data, and the detection sensitivity of the method is higher than that of the traditional code-phase difference sequence method, which is suitable for single frequency RTK positioning technology.

Cycle slips detection; single frequency RTK; Doppler observation; difference sequence; hypothetic check

10.13442/j.gnss.1008-9268.2017.05.014

P228.4

A

1008-9268(2017)05-0068-06

2017-08-28

联系人: 金星E-mail: jin102008@163.com

金星(1992-),男,硕士研究生,主要研究方向为GNSS高精度定位。

王玲(1962-),女,教授,博士生导师,主要研究方向为现代通信与网络技术等。

黄文德(1981-),男,博士,讲师,主要从事航天器轨道动力学及卫星导航系统技术研究。