风险管理与投资决定
李永辉
上次粗略谈到投资理财和培育子女的风险及可以考虑的选项,这次让我们再讨论一下有关风险的一些概念及面对风险考虑决策的一些有趣问题。
首先,风险一般都可被视为不确定性 (Uncertainty)。由此可见,所有我们不能完全控制结果的事情都存在风险,而“风险”一词给人们一般的印象都是较负面。其实,从统计学的角度来看,以x轴表示数值而以y轴表示出现对应该x数值出现的频率 (Frequency),任何偏离x = Mean(x) 的情况都是风险 (σ)。故此,风险可以是出现比预期差的结果,也可以是出现比预期好的结果,而在结果符合正态分布 (Normal Distribution) 的情况下,两者出现的机会更是均等的。故此,风险也应该是一个中性的名词。当然,我们要管理的主要在 Mean(x) 左方,即带来更差结果的风险罢了。
我们很多时候都会听到“固有风险” (Inherent Risk) 及“剩余风险”(Residual Risk),但一般人可能不太理解。固有风险可理解成一件事情 (如一种业务) 在我们没有采取内部控制措施的情况下自然存在的风险,而剩余风险就是我们采取了适当的内部控制措施后仍会继续存在的风险。举个例说,如我们打算经营一家餐厅的话,售出的食品便存在食材变质这个固有风险,即是说,除非我们不出售食品,否则一出售的话,食品含有变质食材这个风险便一定存在。鉴于此,我们须要引入一些内部控制措施 (即在自己控制笵围内可进行的风险控制步骤),如要求员工检查食材必须储存于冰箱内,冰箱内加设独立温度计确保温度为合适水平,必须分开处理生及熟的食物,甚至摆盆子前必须先试味,这些都是可考虑的内部控制措施。采取了这些措施后,售出变质食物的风险便大幅降低,但机率也不会是零,因为人为操作上的失误或机器的失效还是会有机会出现的。这时,我们便可审视剩余风险了。如果剩余的风险已没有办法再进一步降低,则我们可以选择接受风险 (Risk Acceptance) 或转移风险 (Risk Transfer)。接受风险的做法可以是接受及同意现时可做的内部控制措施已是目前最好的措施,并订立下一次检讨的时限,到时检视出售了变质食品的次数及带来的后果,如客人投诉、被媒体报导、赔偿、罚款、销售损失 (Loss of Sales) 等;检讨有否新的内部控制措施可供实施 (如新型号拥有更可靠温度控制的冰箱,或提供更长时间不受干扰电力的后备紧急电源),再决定下一步做法。转移风险一般可以是购买保险,即以一定金额的保费来换取万一出事时的保险金。当然,如剩余风险还是高到一个不能接受或不能转移的程度,那可能我们便需考虑经营另一门生意了。
同样,养育子女时我们也会面对类似情况,上次提到小孩生病可能影响上课学习的风险,这也是固有风险,而我们可以做的内控措施便是替他们安排接种疫苗,或是鼓励他们均衡饮食及多做运动,注意个人卫生,等等。当然这并不能杜绝他们生病的机会,但却可以由于提升免疫力而大幅降低感染传染病的机会,从而尽量降低剩余风险。作为家长,相信大部分人都已自自然然地在实行这些措施,但可能不太多的人会联想到这些其实都是我们正在应对风险的内控措施。这里需要指出,作为一个理性的投资者 (Rational Investor),我们所做的决策及行动背后都应该是有目的及有合理证据支持的,而不是盲从或迷信甚至受羊群心态支配,更不应不进行思考而作出随机 (Random) 决定。
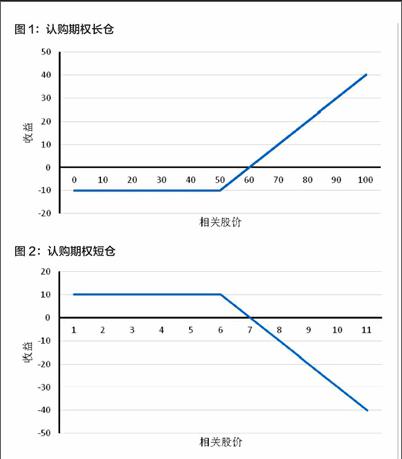
当剩余风险出现而达到不好的结果 (Undesirable Outcome) 时,我们首先需要预测最坏情况是什么,这个除了能帮助我们作出适当的决定外,也能管理我们的期望 (Managing expectation) 。对一般投资而言,我们可以用到“收益图”(Payoff Diagram),其中以x轴表示不同的外在情况,以y轴表示我们的损益 (Profit and Loss)。以投资股票期权为例,认购期权 (Call Option) 的长仓 (Long Position) 及短仓 (Short Position) 便有完全不同的收益图 ,如图1、图2所示。
由图中可见,两者的收益是相反的,也是一个镜像 (Mirror Image),亦可见做认购期权长仓 (图1),最坏情况就只是亏掉期权金 (Option Premium),因为即使相关股票价格跌至零,期权只会变得毫无价值,但你并不会因此欠对家什么。相反,如果我们做的是认购期权短仓 (图2),亦即是我們向对家 (Counterparty) 沽出认购期权。这时,假如到了到期日(Expiry Date) ,相关股票价格升到无限大 (当然实际上股票价格不会是数学上的无限大),我们的亏损便是无限大了,因为对家可以用该期权的行使价 (Strike Price) 来向你购入约定的股票数量。简单举例说,如你沽出的期权是对家可以在3个月后以 $100购入1股的股票A,而期权金是$10。如到了3个月后该股票涨到 $150,那你的亏损便是 $40了,因为你需要用$150的价格在市场上购入1股A来交付 (Deliver) 给对家,但只能收取对家的行使价 ($100),加上先前收取的期权金 ($10),所以你的收益便是 $100 + $10 - $150 = –$40 (亏损40)了。如果到期日时该股票涨到 $1,000,那么你的收益便成了 $100 + $10 - $1,000 =–$890 (亏损 $890)了。这只是个简化的例子,但也可说明不同的决策带来不同的潜在收益,而我们绝对需要知道最坏结果是什么。
当清楚知道可能发生的最坏情况后,我们便要考虑有什么对策,亦即有什么选择 (Alternatives)。要止损 (Stop Loss)、对冲 (Hedging),还是相信本来的决定而不进行更改?要做这些决定并不容易,我们应该科学地和有系统地审视每一种选择将会导致的结果 (也即损益) 及他们出现的机率 (Probability) ,来协助自己分析当前情况,而不是理所当然地或纯粹本能地认为某一选项是唯一选项。这些决定一般可用“期望值 (Expected Value) ”或“效用 (Utility) ”来分析。
一般人都很容易理解期望值,例如某件事情A发生的机率为pA 而 (0≤PA≤1,而其带来的损益为XA,那么A的期望值便是PA*XA。举例说,如你到赌场玩轮盘,下注 $100到红色格子,小铁球落在红色格子的机率为0.5 (简单点先不理会00号),赔率为1︰1,那么期望的收益便是0.5 × $200 = $100,亦即一个公平游戏 (Fair Game)。当然事实上赌场进行的并不会是 Fair Game,而是更类似赌博,即“庄家 (Banker) ”从不同结果 (Outcome) 的赔率上进行“套利”(Arbitrage) 活动。玩“骰宝的桌子上投注“大”及“小”的赔率均为1︰1,看上去似是Fair Game,但是从可发生的6 × 6 ×6 = 216 个结果中,就有6个“围骰”(由赌场“通吃”) 的可能,所以买“大”及“小”的期望值是要比公平值小一点的。由于开出4~10 (扣除围骰) 方为“小”,所以出现“小”的机率其实只有 [(6 × 6 × 6 - 6) / 2] / 216 = 0.486111 而不是0.5,这也表示赌场本质上 (Intrinsically) 已赢了1 - 2× 0.486111 = 2.7778%。而投注在“围骰”的情况更甚,比如“围1”(掷出的3颗骰子均为1) 的赔率为1︰150 ,但是其出现机率其实只有1︰216 (即0.00463),这意味着你每投注216次 (假设每次$100),于投注 $21,600 后便预期能赢取一次 $15,000了。这时,相信很容易便能想像赌场在这里的优势便高达1 - 151×0.00463 = 30.09%。即使外国有些赌场的指定围骰 (如围1) 的赔率为1︰180,赌场的优势仍然高达1 - 181×0.00463 = 16.20%。
说到这里,理性的投资者 (Rational Investor) 似乎都应该清楚地了解到,去赌场投注的期望值并不会对投注人有利,那么为什么还有这么多人喜欢去赌场呢?先撇开赌徒的心理因素及他们以赌博为“娱乐”的心态 (既然是娱乐当然要付出一些“溢价” (Premium) 吧),我们也可以从Utility 的角度来理解人们作出数学上并不合理的决定背后的原因。试想想下列情况:假如你中了一个彩票,而现在你有2个选择,一是肯定赢取 $100;二是有50%机会赢取 $200,同时有50%机会一无所有。两者的期望值均为 $50 (情况1的期望值 = 1×$100,情况2的期望值 = 0.5×$200 + 0.5 ×$0)。而以往的研究大部分结果 (如 Kahneman and Tversky) 都是比较多受访者倾向选择1。既然两者的期望值一样,那一定是有其他因素影响我们的选择,而 Utility 便是其中一种解析。普遍认为倾向选择1的人比较厌恶风险 (Risk Averse) ,他们宁可锁定自己的利润 (Profit Taking) 而不愿承受更高风险来达到更高利润。这个也是因为在这些人心目中,赢得 $200带来的满足喜悦并不是赢得 $100的2倍或以上,亦即 U(200) ≤2×U(100)。再来看一个类似情况,假如我们因合约纠纷被控告到法院,我们有2个选择,一是赔偿 $10,000 作为和解代价;二是选择打官司 (假设不用律师费用),而打官司的结果有50%胜算而不用赔偿,但同时有50%机率败诉而要赔偿 $20,000。研究也指出大部分于先前彩票的例子中选择了前者的人这时会倾向选择后者。而很明显,在这个官司的例子中,两个选择的期望值是一样的 (选择前者的期望值 = 1 ×-$10,000,选择后者的期望值 = 0.5 ×0 + 0.5×-$20,000)。这样与彩票例子的取向便相反了,这也道出了一般人对损失的感觉往往比利益来得敏感。故此,可以发现原来大部分人都倾向锁定利润,而不倾向锁定亏损。在投资市场上我们也很容易看到这种现象,那就是股票价格涨了5%~10%便急于平仓获利,反之跌了20%还死抱着股票而不平仓止损的情况比比皆是。换句话说,很多原来的风险厌恶者在面对亏损的时候便会变成风险爱好者 (Risk Lover)。 Utility 同时亦解释了为什么香港“六合彩”受欢迎的原因,买“六合彩”的人都知道中头奖的机会很低很低,同样“庄家”(即香港赛马会) 从赔率上占绝对优势,但投注的人仍会乐此不疲,就是因为他们会认为即使不中奖,损失 $10 (一注) 也无关痛痒,但万一 (其实远低于万分之一,简化一点不计算“特别号码”的话,从49个号码中选中6个号码的机率仅为49! / (49-6)!6! = 1 / 13,983,816,即约一千四百万分之一、而中了头奖数千万的话,带来的喜悦则会是无与伦比 (Unparalleled) 地高,故此才有买“六合彩”这种行为。
再者,行为金融学 (Behavioral Finance) 已提出一般人都会出现“过度自信”(Over-Confidence),亦即比較倾向相信自己做出的决定为正确的决定。曾有心理学研究 (Ola Swenson) 受访的驾驶者认为自己的驾驶技术如何,结果发现竟然高达93% 的受访者认为自己的驾驶技术“高于平均水平”(Above Average),而事实上只会有50%的驾驶者会拥有高于平均水平的驾驶技术,而另外50% 则必然是低于平均水平的。故此,一般人面对亏损时,都有可能倾向认为自己本来的决定是正确的而选择继续持有亏损的投资,而非客观地从新审视当前情况而决定是否该改变策略。说到这里,重点是要“重新审视当前情况”,所以一方面要有纪律严守止损,但也不能是盲目抛售。在这种情况下很多人都会陷入“趋势” (Trend) 的谬误,或称为“赌徒的谬误” (Gamblers Fallacy),如认为已走到下降轨的股票将继续下跌,反之亦然。但其实股票价格涨跌的原因不胜枚举,除了基础因素外,市场消息、大户的策略部署以至散户的情绪都会影响整个市场气氛。故此,趋势研究并不是灵丹妙药。有研究以完全随机事件来比喻股票价格的涨跌,我们先撇开这个是否是一个百分百洽当的比喻,但某种程度上从结果来看也有些接近。同样以刚才骰宝的例子,试想想,在赌场中骰宝桌显示刚才已连续开出了10次“大”,这时会有部分人 (更多可能是大部分人) 会在第11局继续投注于“大”,原因是他们认为开“大”会比较“旺”,故此会做出“趁势”的决定;同时,也有部分人会认为已开出了这么多次“大”,这次开出的该是“小”了罢;当中更会有一些略懂数学的人认为,连续开出11次“大”的机会是很小的,从上文提到每一次掷出“大”的机率为48.6111%,那么连续掷出11次“大”的机率则只有48.6111%^11 = 0.0003582或0.03582%,所以便应该投注于“小”。究竟哪一种想法比较可取?我们首先要弄清楚掷骰子的第n 次与第n+1 次的结果之间有什么关联,为什么我们会认为第1次与第2次之间没有关联,但当观察了10局之后会突然“领悟”到第11局的结果会与之前的连续10局有关?这就是堕入了趋势的谬误了。掷骰子第n次与第n+1次的结果很明显是独立事件 (Independent Event) ,并不会互相影响,而每一次都是一次个别的随机 (Random) 事件,骰子自己并不会有记忆而储存自己之前的掷出结果,更不会有力量令自己的掷出结果在某个掷出的次数内符合机率的预期并纠正之前的偏差。但人们总喜欢想当然地尝试“发现”(Uncover) 他们当中的关联,即使他们本来就知道他们根本没有任何关联。
总结一下,话题虽然好像拉到了很远,但这些都和投资理财息息相关:我们要有系统地理性分析现状,预算可能出现的状况,找出可能对应的选项,再审视每一个选项的结果和出现的机率,作出客观的决定。要做到这一点并不容易,毕竟我们不是机器,感情、情绪、贪婪、恐惧,都不时挑战我们的客观分析,更往往占了上风。有投资专家提醒投资者不要和股票“谈恋爱”,不无道理。有不少投资者因为某股票曾替他们赢得第一桶金,以后便“爱上了”这股票,即使客观分析有其他股票更值得投资,他们都会与它“长相厮守”。也有人会拿一些看似客观或科学化的数字来继续欺骗自己,如有人于爱股持续下跌后对别人说 (其实也是对自己说):即使股价跌了不少,但看看派息率每年有 5% 也算不俗了。他们应该想想,如股价再下跌50%而派息金额不变,派息率更将升至 10%,这个又是否是他们乐于见到的结果呢?又或者,如他们心爱的股票原来的派息率为每年 5%,而最近股价涨了一倍,他们又会否埋怨派息率下跌了 50% 到每年只有2.5%呢?
最后,要解析种种看似理性的人为何往往会作出不理性的决定,行为金融学对之有很多值得参考及借鉴的见解,希望往后有机会能和大家讨论一下。反复思考,温故知新,总是有趣的。

