重叠纤类图像的凹点匹配和分割算法
陈晓春, 张彦彬,2, 彭 虎,3, 陈 翔,3, 褚乃清
(1. 深圳清华大学研究院 电子设计自动化实验室, 广东 深圳 518057; 2. 哈尔滨工业大学(深圳), 广东 深圳 518055; 3. 中山大学, 广东 广州 510275; 4. 深圳出入境检验检疫局 工业品检测技术中心, 广东 深圳 518045)
重叠纤类图像的凹点匹配和分割算法
陈晓春1, 张彦彬1,2, 彭 虎1,3, 陈 翔1,3, 褚乃清4
(1. 深圳清华大学研究院 电子设计自动化实验室, 广东 深圳 518057; 2. 哈尔滨工业大学(深圳), 广东 深圳 518055; 3. 中山大学, 广东 广州 510275; 4. 深圳出入境检验检疫局 工业品检测技术中心, 广东 深圳 518045)
为解决混纺纤维类图像中多根纤维的分离和识别难题,提出一种基于凹点匹配的新方案来实现重叠纤维分割。在图像轮廓寻找角点,利用三角形矢量面积法找到角点中包含的凹点;通过凹点、该凹点的前继点(或后继点)和目标凹点构成的三角形,结合凹点的几何特征来判断该凹点和目标凹点是否匹配;通过将匹配凹点连线来实现图像中的纤维分割。与现有分割算法相比,新方法采用了凹点距离和三角形构造原理相结合的机制来实现匹配。结果表明,该算法可适用于多根纤维相互黏连或交叉的复杂场景,且有较高的分割精度。
图像分割; 重叠纤维; 角点; 矢量三角形面积; 凹点匹配
目前国内出入境检验检疫单位对混纺纤维的识别,一般由工程师通过显微镜放大样品图像后人工判断来实现,不仅耗费大量人力,而且效率低下,有较高的自动化识别技术需求。现有智能化纤维识别技术大都依赖于多项特征指标提取,如棉纤维的纵向和横截面特征,或通过提取纤维宽度并测量纵向宽度变化作为特征参数[1-2]。这些指标往往基于对单根纤维的精确测量,但实际检测中所获取的样本图片中往往存在多根纤维交叉和黏连现象,因此研究如何对重叠图像分割是首要解决的问题[3-4]。
传统的纤维图像分割方法有形态学图像处理方法[5]、分水岭方法[6]及基于交叉处各分支斜率的分离方法[7]等。数学形态学方法通过膨胀腐蚀获取纤维的轮廓边缘曲线,但是膨胀和腐蚀的次数需要人工指定,不仅效率低并且有一定的误差存在。分水岭方法虽计算简单且精度高,但对噪声过于敏感,往往产生严重的过分割结果。基于交叉分支斜率的方法用相近的边缘斜率进行匹配,但仅对3根以内的交叉纤维分割的正确率较高,故此类方法在实际的纤维重叠图像中并不实用。
本文研究提出一种基于轮廓凹点匹配的分割方法,利用纤维重叠区域所产生的凸多边形特性与轮廓凹点之间的关联性对凹点匹配,用匹配上的凹点对重叠纤维图像分割。结果表明,本文算法可在不改变纤维轮廓特征的前提下,快速实现纤维自动化分割。
1 前期处理
1.1图像预处理
光学显微镜拍摄的纤维图像存在亮度不均以及放大后的边缘模糊等现象,影响了图像在输出时的正确性。而且纤维轮廓图像的数字化误差和噪声的影响会造成轮廓线不平滑和灰度深浅不一等现象,这样会导致最终得到的轮廓线不连续,因此首先要对纤维图像去噪[8-9]及平滑处理轮廓曲线,使得纤维的图像信息可准确再现。
采用B样条曲面拟合[10]与复数域滤波方法[11]对显微镜下拍摄的纤维图像进行预处理。在最小二乘法准则的约束下,采用双三次B样条曲面拟合得到图像背景,用原始纤维图像减去拟合背景得到目标图像,达到去除图像背景和解决光照不均的效果;采用复数域非线性各向异性扩散滤波,可在消除图像噪声的同时,保证边缘信息的完整性。再对目标图像进行二值边缘提取,对二值化后的图像进行形态学运算及纤维内部填充处理,其中包括5次复域非线性各向异性扩散滤波迭代处理。处理过程如图1(a)~(d)所示。经过以上处理可得到边缘较为光滑的纤维二值图像,如图1(e)所示。为获取轮廓角点再对其进行二值轮廓提取,结果如图1(f)所示。

图1 图像预处理Fig.1 Image preprocessing. (a) Original image; (b) B-spline surface fitting;(c) Real domain; (d) Complex domain;(e) Fiber binary image; (f) Fiber contour image
1.2轮廓角点的提取
角点即图像轮廓曲线的曲率极大值点。对于连续的曲线,可直接利用数学上的定义来计算其曲率,而数字曲线由一组离散整数坐标点组成,因其离散特性,不能直接计算轮廓曲线上各像素点的曲率,故需采用离散曲率计算公式来计算各像素点的曲率值大小。常用的离散曲率计算方法有增量曲率[12]、点到弦距离累加[13]、K余弦曲率[14-15]等。
K余弦曲率算法作为计算离散曲率最著名的方法之一,至今仍被广为使用。将第t条轮廓曲线表示为
Lt={Pi(xi,yi)|i=1,2,3,…,n}
(1)
式中:n为第t条轮廓线上轮廓点的个数。如图2中轮廓曲线,取点Pi(xi,yi),在该点取前、后第k个像素点坐标Pi-k(xi-k,yi-k)和Pi+k(xi+k,yi+k),令
αi(k)=(xi-xi-k,yi-yi-k)
βi(k)=(xi-xi+k,yi-yi+k)
设点Pi的2个向量αi(k)、βi(k)夹角余弦值为
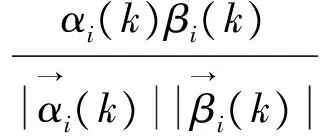
(2)
在Pi两侧计算曲线上所有点与Pi形成的向量夹角的余弦值并进行比较,找出余弦值最大的夹角,其余弦值记作Cmax,记录下当前K值记作KM。满足Ci+KM(K)具有最大的余弦值。曲率的极大值点应满足余弦值极大。设定阈值CT,拥有余弦值超过CT的点认为是曲率极大值点,即轮廓曲线上的角点。由此便完成了角点的提取工作。
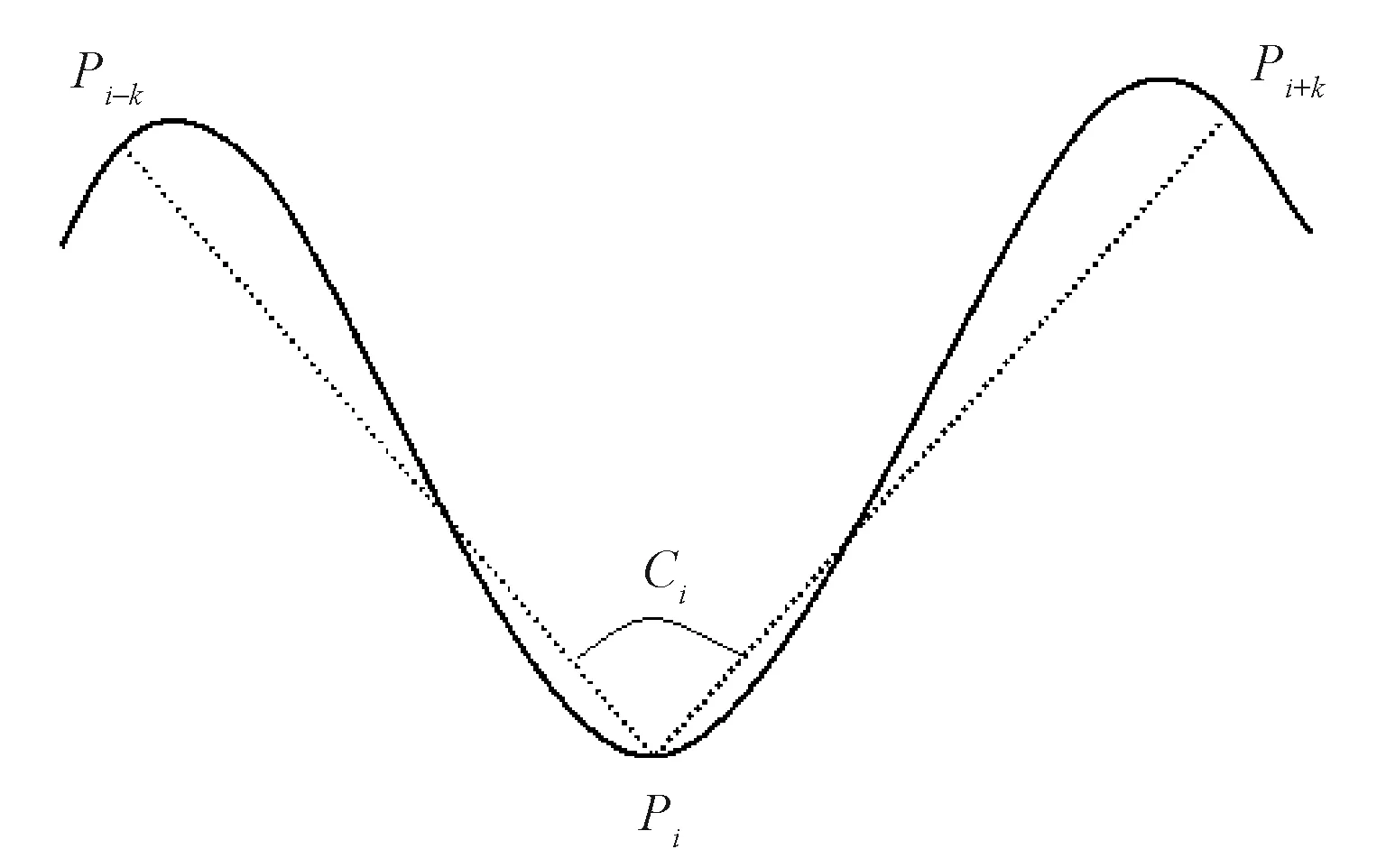
图2 K余弦曲率算法Fig.2 K-Cosine curvature algorithm
1.3轮廓凹点的确定
轮廓角点分为凸点和凹点2类,采用矢量三角形面积法来确定边界上的凹点。
由图像拐点Pi(x0,y0)与该点相距m个像素的前继点Pi-m(x1,y1)和后继点Pi+m(x2,y2)围成一个矢量三角形,利用式(3)计算此三角形面积Si。
(3)
本文研究中轮廓点的坐标按逆时针存储,如果角点Pi与其前继点和后继点围成的三角形的面积Si<0,那么可判断该角点为凹点,如图3(a)所示;如果Si>0,可判断该角点Pi为凸点,如图3(b)所示。由该方法提取的凹点集合按序存放到数组集中。
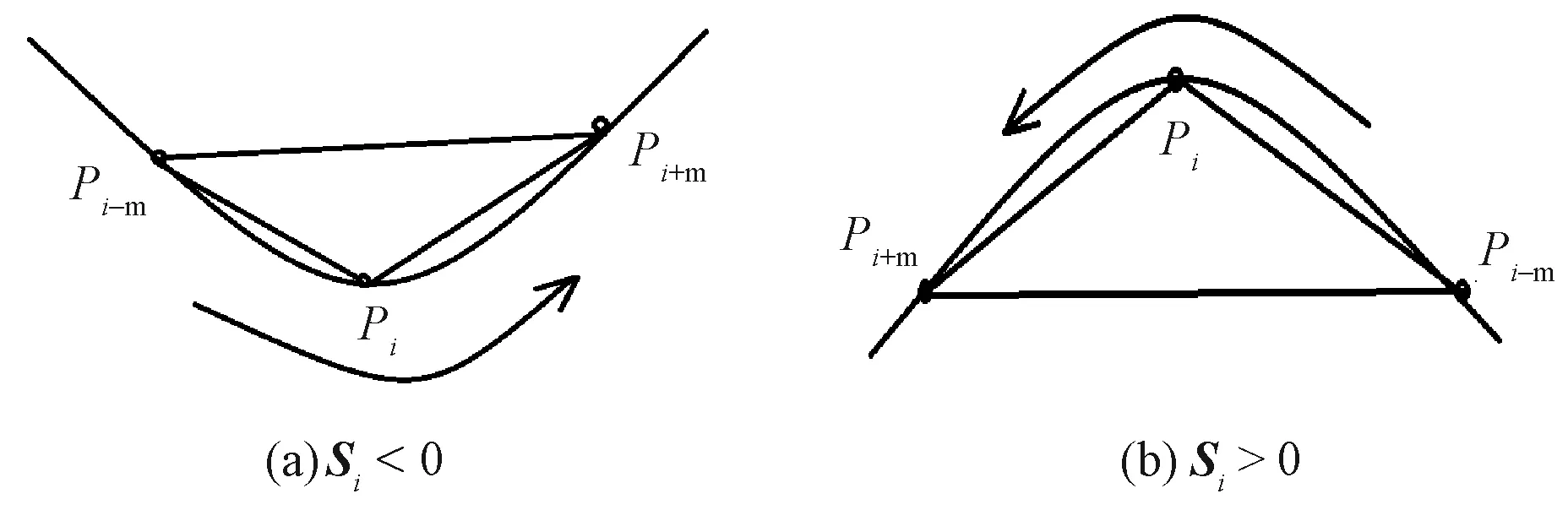
图3 矢量三角形面积法Fig.3 Vector triangle area method
2 凹点匹配算法描述
2.1算法流程
对于交叉型的纤维重叠区域通常有4个凹点,黏连型通常有2个凹点。本文提出凹点匹配的新算法,可将纤维交叉、黏连处的凹点匹配,通过在二值图中将匹配上的凹点相连,达到分离重叠纤维的目的。算法的主要流程如下所述。
步骤1:从凹点集中的第1个凹点开始依次判断,为每个凹点找到其匹配凹点。假设当前凹点为Pi,首先找到它在轮廓线上的坐标和序号;然后对所有其他轮廓凹点Pj(j≠i)进行匹配判断。若Pi和Pj之间存在其他角点,则它们可能为匹配凹点,进行第2步判断;否则认为匹配不成功,继续与下一个凹点Pj+1进行匹配判断。
步骤2:若Pi和Pj连线的中点在纤维的轮廓曲线内部,继续进行第3步判断;否则,认为匹配不成功,继续与下一个凹点进行匹配判断。
步骤3:设当前检测凹点为Pi(x,y),Pi-m(xi-m,yi-m)和Pi+m(xi+m,yi+m)分别是与Pi等间距的前继点和后继点。首先让Pi、Pi-m和Pj构成三角形△PiPi-mPj;计算Pi与Pi-m的距离D1,Pi与Pj的距离D2及Pi-m与Pj的距离D3。若满足:
0≤(D1+D2)-D3 (4) 认为Pi与Pj匹配成功,将Pi与Pj存进匹配数组match1。式(4)中,T为线性判断阈值,本文中T取2。同样对于后继点Pi+m可构造三角形△PiPi+mPj,计算相应距离。若也能得到类似上式结果,则认为Pi与Pj匹配成功,将Pi与Pj存进匹配数组match2。由条件约束,上式仅有1个成立。若都不成立,认为匹配不成功,继续与下一个凹点进行匹配判断。 步骤4:重复以上步骤遍历所有凹点,即可将所有凹点进行匹配。 在上述匹配过程中,存在同一个凹点与多个凹点均满足匹配条件的可能性,保留其中距离最近的一组凹点作匹配结果。最后将match1与match 2结合作为凹点的最终匹配结果。 2.2算法说明 由纤维的轮廓特征可看出,每根纤维的外轮廓都是一个凸多边形。由计算机图形学可知,对任意凸多边形满足: 1)凸多边形所有顶点均为凸点,即所有内角小于180°。即对凸多边形内任意一个内角α满足: α<180° (5) 2)设Pi、Pj为凸多边形上的任意2个顶点,在其内部取点PM,若满足: PM=ηPi+(1-η)Pj (6) 则PM必落在该凸多边形内部,式中0≤η≤1。 对于步骤1:显然平面上给定2个凸多边形,其交集仍是一个凸多边形。故2个纤维轮廓交叠在一起的重叠部分为一个凸多边形,其顶点中的交叉点即为纤维的轮廓凹点。由于相邻2个凹点之间的轮廓曲线上包含着至少1个凸多边形边界,由此纤维重叠位置处属于同一轮廓曲线的相邻2个凹点之间存在至少1个凸点。 对于步骤2:常用的点与多边形的关系判断方法有差积判别法、夹角法和射线法等[16]。由式(6)可知,任意2个凹点连线中点必在纤维重叠区内部。纤维的二值图像可表示为 (7) 式中Tb为二值化阈值。 对同一重叠区任意2个凹点A(xa,ya)与B(xb,yb),它们的连线中点满足: (8) 对于步骤3:三角形是由同一平面内不在同一直线上的3个顶点顺次连接所组成的封闭图形。运用这个性质对凹点进行匹配判断。若2个凹点Pi与Pj(i≠j)在同一根纤维边缘轮廓上,由于纤维的边缘轮廓曲率较为平缓,它们的连线与纤维边缘轮廓线几乎重合,接近于直线。在Pi、Pj所在纤维轮廓,取与Pi相差m个像素(本文取m=10)的前继点Pi-m,则Pi-m、Pi、Pj在同一直线上,满足: 0≤(|Pi-mPi|+|PiPj|)-|Pi-mPj| (9) 若Pi、Pj不在同一根纤维轮廓上,则Pi-m、Pi、Pj不在同一直线上,满足: (|Pi-mPi|+|PiPj|)-|Pi-mPj|>T (10) 再取与Pi相差m个像素的后继点Pi+m,用同样的方法可将Pi的另一个相匹配的凹点找到。 如图4所示,{P1,P2}和{P1,P4}是属于同一根纤维的同侧轮廓线上的2对匹配点,{P1,P3}不是匹配点。以凹点P1为例说明其匹配过程:在P1左侧取相差10个像素的前继点PL,右侧取同样距离的后继点PR。构造三角形△P1PLP2,由于PL、P1、P2这3个点在同一纤维轮廓上,故3点满足:0≤(|PLP1|+|P1P2|)-|PLP2|<2。其他轮廓凹点P3、P4与P1和其前继点PL均不在同一直线上,所以P3满足:|PLP1|+|P1P3|-|PLP3|>2,同理P4满足:|PLP1|+|P1P4|-|PLP4|>2。由此可见前继点PL的引入使得P1找到了与其相匹配的轮廓凹点P2。同理后继点PR的引入使P1找到另一个匹配凹点P4。 图4 匹配过程Fig.4 Matching process 3.1分割情况分析 仿真实验在MatLab编译环境下完成,图5(a)示出4根纤维的准确分割过程,图5(b)、(c)分别展示了由凹点匹配出错导致的过分割和欠分割情况。 在图5(a)所包含的4根纤维中,有1根分离式孤立纤维。利用连通域原理可将其快速找到,对另3根重叠纤维利用匹配凹点作直线进行分割。由分割结果可见,该分割算法能在分离纤维的基础上,最大化地保留原始纤维图像的轮廓特征,这将有利于后续的纤维识别工作。 在此定义分割率Sr为 (11) 注:A为未分割的原始纤维图像; B, C, D, E, F, G分别对应各种情况下原始纤维图像A分割出的单根纤维。图5 重叠纤维图像的分割Fig.5 Segmentation of overlapped fibers image; (a) Segmentation of four overlapped fibers; (b) Under-segmentation caused by concave point matching error;(c) Over-segmentation caused by concave point matching error 式中:Nr为结果中正确分割的纤维个数;Nf为重叠纤维实际的纤维个数。用Sr衡量该算法分割的效果,Sr越大,表示被准确分割的纤维个数越多,分割的效果越好。 在图5(b)中实际包含5根黏连纤维,但在结果中只分离出了4根。在凹点匹配过程中,其中2个凹点由于黏连位置处的2个凹点间线段距离相对过长,并且顶部凹点的前继点(或后继点)和目标点之间难以构成直线关系,导致用本文算法失效。究其原因,这与图像预处理时膨胀过程导致部分面积很小的锐角区域被平滑和填充,使得凹点特征被弱化有关,因此在图像预处理中借用B样条取得轮廓时,应尽量减少或避免膨胀类数学形态学处理。 图5(c)中实际有5根黏连纤维,但是实际却只分割出6根纤维,其原因在于2个不匹配凹点周围的纤维轮廓线特征相近,此外它们又刚好集中在一狭小面积区域内,导致2点和他们的前继点或后继点连线接近于直线,从而出现错误匹配,使得分割根数大于实际根数情况。此处可对算法作改进,即对于有关联匹配的凹点按像素的坐标值排序。如对于图5(c)中的交叉型凹点集按照坐标大小及逆时针方向,如{左,下,右,上}对4个点排序,并禁止对非相邻凹点连线分割纤维,于是问题得以解决。 此外,伪角点的存在有时也会产生错误匹配,导致过分割现象,需在提取角点过程中加以剔除,本文主要通过设置阈值来剔除伪角点。 3.2伪角点的剔除 真正的角点往往存在轮廓曲线的尖角处,而伪角点一般存在于纤维两侧光滑轮廓曲线上。由于局部噪声的影响,使得曲线上产生了一个局部尖角。在很小的范围内,伪角点处的角度变化很大,曲率很大,故被误判为伪角点。伪角点分为伪凹点及伪凸点2类。如图6所示,T1、T2和T3为2种不同类型的伪角点,其中T1为1个伪凸点,T2和T3为2个伪凹点。伪凸点可通过矢量三角形面积的正负排除;伪凹点可通过矢量三角形面积的大小进行排除。故通过控制矢量三角形的面积阈值可在一定程度上减少伪角点的数量。 图6 包含伪角点的纤维二值图Fig.6 Fiber binary image including false corners 图7示出不同的面积阈值下,3~5根纤维凹点检测的准确率统计,可得出将阈值设置为15时,凹点检测的准确率为最高,并且此阈值下的准确率不随根数变化而减小。原因在于虽然纤维重叠个数不同,但伪角点与纤维两边轮廓所围成的面积相近。 图7 面积阈值的选取Fig.7 Choice of area thresholds 3.3实验结果分析 通过对大量样本测试,该算法对包含1~5根重叠纤维的图像进行分割的准确性统计,结果如表1所示。对于1~2根重叠纤维图像,几乎都可正确分割,故没有在表中统计。对于3~5根纤维图像中凹点检测、匹配和分割的结果如表1所示。随着纤维数量增加,纤维的分布更加复杂,凹点的匹配率降低,导致分割的效果有一定程度的下降,但分割的成功率仍可维持在80%以上,证明该算法具有一定的稳定性。如表1所示,分割率与凹点匹配的准确率相关,与检测到凹点的准确性也是密不可分的。 表1 图像分割准确率结果统计Tab.1 Results statistics on image segmentation % 针对多根纤维交叉、黏连等重叠现象,提出了基于凹点匹配的重叠纤维分割算法。利用纤维图像重叠区域凹点之间的特征关系,以及凹点、前继(后继)点和待匹配凹点构成的三角形边长关系,将属于同一纤维轮廓的特征凹点匹配,再用匹配上的凹点对重叠纤维进行分割。结果表明,本文算法可解决多根纤维相互黏连或交叉重叠时不易分离和分割不精确等问题。本文算法不仅适用于提取重叠型纤维图像中对应重叠边界处的凹点,而且可通过匹配算法实现重叠纤维的分割,在复杂重叠情况下,纤维分割成功率可达80%以上。 FZXB [1] 应乐斌, 戴连奎. 基于纤维纵向显微图像的棉/亚麻单纤维识别[J].纺织学报, 2012,33(4): 12-18. YING Lebin, DAI Liankui. Single fiber identification of cotton/flax fabric based on longitudinal view of microscopic fiber images [J]. Journal of Textile Research, 2012, 33(4): 12-18. [2] 任帅杰,张文生,何源.基于图像分析的纤维直径和曲率的测量方法[J].中国图象图形学报,2008, 13(6):1153-1158. REN Shuaijie, ZHANG Wensheng,HE Yuan. Measuring diameter and curvature of fibers based on image analysis[J]. Journal of Image and Graphics, 2008, 13(6):1153-1158. [3] ZHOU Zhiheng, DAI Ming, ZHONG Huiqiang. Parametric shape prior model used in image segment-ation[J]. Journal of Systems Engineering & Electronics, 2016, 27(5):1115-1121. [5] RUBERTO C D, DEMPSTER A G, KHAN S, et al. Analysis of infected blood cell images using morphological operators[J]. Image and Vision Computing, 2002, 20(2): 133-146. [6] GRAU V, MEWES A U, ALCANIZ M, et al. Improved watershed transform for medical image segmentation using prior information[J]. IEEE Transactions on Medical Imaging, 2004, 23(4): 447-458. [7] RIZVANDI N B, PIŽURICA A, PHILIPS W. Automatic individual detection and separation of multiple overlapped nematode worms using skeleton analysis[C]//Image Analysis and Recognition. Berlin: Springer, 2008:37-42. [8] GONZALEZ R C, WOODS R E, EDDINS S L. Digital Image Processing Using MatLab[M]. Upper Saddle River: Prentice Hall, 2004:65-140. [9] MILLER M A, KINGSBURY N. Image denoising using derotated complex wavelet coefficients[J]. IEEE Transactions on Image Processing, 2008, 17(9): 1500-1511. [10] 余成波, 秦华峰, 张莲.基于B样条函数的图像分割分水岭算法研究[J].压电与声光,2008,30(3):356-358. YU Chengbo, QIN Huafeng, ZHANG Lian. Watershed algorithm research of image segmentation based on B-spline function[J]. Piezoelectrics & Acoustooptics,2008, 30(3):356-358. [11] GILBOA G, SOCHEN N. Image enhancement and denoising by complex diffusion processes[J]. Pattern Analysis & Machine Intelligence IEEE Transactions on, 2004, 26(8):1020-1036. [12] FREEMAN H, DAVIS L S. A corner-finding algorithm for chain-coded curves[J]. Computers IEEE Transactions On, 1977,26(3):297-303. [13] AWRANGJEB M, LU G. Robust image corner detection based on the chord-to-point distance accumulation technique[J]. IEEE Transactions on Multimedia,2008,10(6):1059-1072. [14] ROSENFELD A, JOHNSTON E. Angle detection on digital curves[J]. IEEE Transactions on Computers, 1973, 22(9):875-878. [15] SUN T H. K-Cosine corner detection[J]. Journal of Computers, 2008, 3(7):16-22. [16] 陈瑞卿, 周健, 虞烈.一种判断点与多边形关系的快速算法[J]. 西安交通大学学报, 2007, 41(1):59-63. CHEN Ruiqing, ZHOU Jian, YU Lie. Fast method to determine spatial relationship between point and polygon[J]. Journal of Xi′an Jiaotong University, 2007, 41(1):59-63. 2017中国纺织学术年会圆满落幕 2017中国纺织学术年会于11月3-5日在武汉成功召开。本届年会以“融智·融创”为主题,由中国纺织工程学会主办,武汉纺织大学承办、富丽达集团股份有限公司协办,并且得到了江南大学、天津工业大学、西安工程大学、中国纺织科学研究院等单位的大力支持。中国科协学会服务中心党委书记、副主任刘亚东,中国纺织工业联合会会长、中国纺织工程学会理事长孙瑞哲,中国科学院院士张俐娜、中国工程院院士孙晋良、蒋士成、俞建勇,中国纺织工业联合会副会长李陵申出席会议。来自美国、日本、澳大利亚、印度、巴基斯坦、中国香港等国家和地区的海内外科技工作者700余人参会。中国纺织工程学会常务副理事长伏广伟和武汉纺织大学教授徐卫林主持主会场开幕式和学术报告。孙瑞哲理事长,张俐娜院士,2016中国纺织学术大奖获得者程博闻教授、王华平研究员做精彩主题报告。会议宣布浙江理工大学教授陈文兴荣获2017中国纺织学术大奖;丁彬等5人荣获2017中国纺织学术带头人称号;廖周荣等5人荣获2017中国纺织技术带头人称号;刘丽芳等3人荣获2017“富丽达”中国纺织青年科技奖。会上还颁发了第18届陈维稷优秀论文奖,2017中科纺织科技成果转化贡献奖,2017年度纺织优秀博士、硕士学位论文奖。同时还向10家中国纺织工程学会科研基地隆重授牌。 2017中国纺织学术年会共设7个分会场,围绕高品质原液着色纤维及其纺织品产业技术创新、现代纺织技术、产业用纺织品-分离膜技术与应用、服装科技创新、国际纺织高等教育论坛等热点内容展开深入交流;同时第3期“青年人才托举工程”沙龙、中国科协第126期新观点新学说学术沙龙暨第12期纺织科技新见解学术沙龙、中国纺织工程学会第25届理事会第五次扩大会议、《纺织学报》第九届编辑委员会第2次会议同期举行。 Concavepointsmatchingandsegmentationalgorithmforoverlappedfiberimage CHEN Xiaochun1, ZHANG Yanbin1,2, PENG Hu1,3, CHEN Xiang1,3, CHU Naiqing4 (1.KeyLaboraryofElectronicsDesignAutomation,ResearchInstituteofTsinghuaUniversityinShenzhen,Shenzhen,Guangdong518057,China; 2.HarbinInstituteofTechnology(Shenzhen),Shenzhen,Guangdong518055,China; 3.SunYat-senUniversity,Guangzhou,Guangdong510275,China; 4.TechnologyCenterforIndustrialProducts,ShenzhenEntry-ExitInspectionandQuarantineBureauTesting,Shenzhen,Guangdong518045,China) In order to identify the different components which are adhered or crossed each other in a hybrid fiber image, a fiber segmentation algorithm based on concave points matching in the overlap area was proposed. The detection of contour corners was firstly obtained, and the vector triangle area method was also used to find contour concave points from the corner set. For a given concave point, the precursor point (or subsequent point) and the target point were selected to form a triangle. The triangle and other significant features were used to judge whether the concave point and target point were matched. At last, by the connection of the matching concave points, the segmentation of overlapped fiber image could be realized. Compared with the existing algorithms of segmentation, the novel method employed a mechanism combined with distance between concave points and triangular construction principle to achieve the purpose of matching. The experimental results show that the algorithm can deal with the situation of adhesive fiber and cross fiber, with high segmentation accuracy over 80% in complicated scenes. fiber image segmentation; overlapped fiber; corner; vector triangle area; concave point matching 10.13475/j.fzxb.20170202107 TP 319;TS 101.9 A 2017-02-14 2017-04-06 广东省教育部产学研项目(2012B091100495); 深圳市基础研究项目(JCYJ20160429170032960) 陈晓春(1972—),男,高级工程师,博士。主要研究方向为数字图像处理、无线通信及其相关集成电路设计。E-mail:chenxc@tsinghua-sz.org。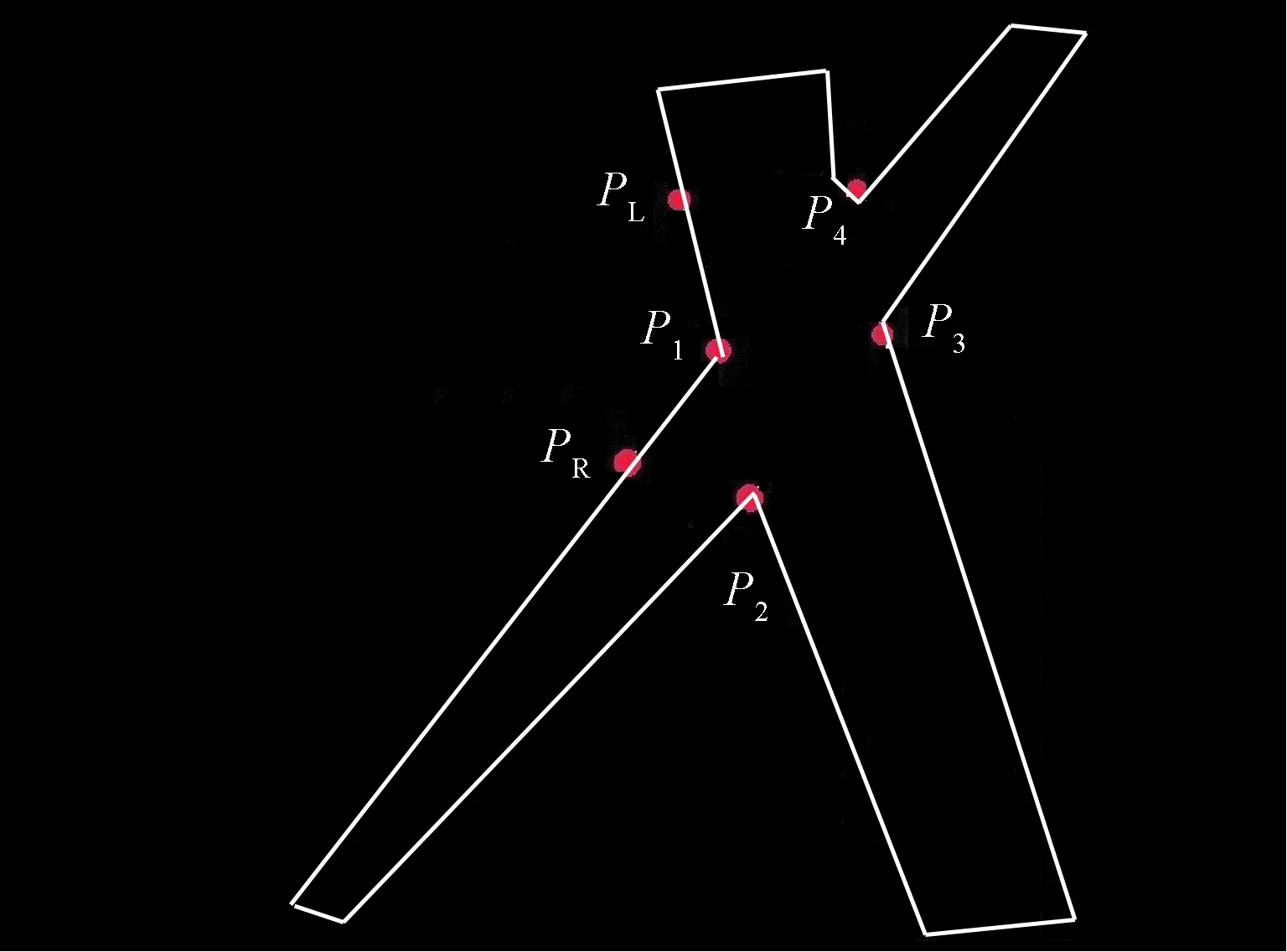
3 实验及结果分析





4 结 论

