含纱疵纱线的气流引纬牵引特性分析

张 荣， 冯志华， 陆 庆， 陈晓明

(苏州大学 机电工程学院， 江苏 苏州 215021)

含纱疵纱线的气流引纬牵引特性分析

张 荣， 冯志华， 陆 庆， 陈晓明

(苏州大学 机电工程学院， 江苏 苏州 215021)

为探究纱疵对气流牵引纱线的影响，根据纱疵在流体中的形状特性，提出以球体或圆柱体模型化短粗节纱疵的新设想。基于Fluent的流场分析结果，对短粗节纱疵牵引力进行了数值计算。通过自行设计的主喷嘴气流引纬牵引力测试装置，测定了短粗节纱疵模型球体在0.3 MPa供气压力下的气流牵引力大小，并对前述数值计算结果的合理性进行了验证，得到较好的一致性。同时，探究了纱疵对纱线牵引力系数的影响效应。结果表明：随着纱疵直径增大，纱线牵引力系数的变化率呈现先上升随后逐渐趋于平缓的现象；而随着纱疵数量的增多，牵引力系数的变化率呈逐次下降态势。

纱线； 纱疵； 气流牵引； 数值计算； 牵引力系数

纱线条干不匀率是评价纱线质量的重要指标之一，对纱线和织物外观质量具有深远的影响。纱线条干不匀常以质量不匀率(线密度不匀率、条干不匀率)、直径不匀率和捻度不匀率等不同的形式表现，其中直径不匀率对纺织品外观质量的影响最突出[1]。迟开龙等[2]以4种不同规格的纯棉纱线为例，提出一种基于数字图像处理技术检测纱线条干不匀率的方法，并证明所提出的纱线条干均匀度检测方法是可行的，可准确高效地检测出纱线的条干不匀值，客观反映纱线的外观质量，依据经形态学运算处理后得到的纱线局部放大图像可发现纱线的直径不匀。

文献[3]中指出纱疵类型按出现概率的不同可分为常发性纱疵和偶发性纱疵，偶发性纱疵的粗细程度较常发性纱疵更为显著，纱疵对纱线的质量影响也越大。毛羽是纱线上的纤维突出部分，国外对纱线毛羽有了一定的研究。Chang等[4]探究了环锭纺中纱管回转时纱线毛羽对能量消耗的影响发现，毛羽长度和毛羽根数对能量消耗起着决定作用，并表明减少纱线毛羽将有助于减少环锭纺的能耗。

为分析气流对纬纱的牵引效应，文献[5-6]基于实验测量，结合Fluent数值计算，较为详尽地分析计算了多种纬纱随气流速度(供气压力)变化的牵引力(系数)，Chen等[7]通过双喷嘴射流性能的探究发现，织机耗气量可进行有效的控制，为织造工艺提供了一定的参考依据，但未涉及纱疵/毛羽对纱线气流牵引特性的影响研究。目前，尚少见纱疵/毛羽对纱线气流引纬影响的研究报道。

纱疵必然影响纱线的质量，进而影响纺织品的质量评定与等级划分。本文研究在文献[5-6]的基础上，围绕不同纱疵类型，结合理论分析与数值计算手段，对气流牵引含纱疵纱线进行数值模拟，并通过实验测试对数值模拟的合理性进行验证，从而探究纱疵对纬纱的气流牵引特性的影响。

1 纱疵等级划分

图1 纱疵对流场速度的影响Fig.1 Effect of yarn fault on airflow. (a) Yarn with long slub faults; (b)Yarn with long thin faults; (c)Yarns with short slub faults.

文献[3]根据瑞士乌斯特公司生产的纱疵分级仪的分级方法，将纱疵分为短粗节、长粗节及长细节3大类，其中，纱疵截面相对原正常纱线截面尺寸粗100%以上、长度在8 cm以下的纱疵称为短粗节；纱疵截面相对原正常纱线截面尺寸粗45%以上、长度在8 cm以上的纱疵称为长粗节；纱疵截面相对原正常纱线截面尺寸细30%～75%、长度在8 cm以上的纱疵称为长细节。在相同的流场中，长粗节、长细节和短粗节对流场速度的影响如图1所示。由图中速度等高线变化可发现，短粗节对流场的影响相对较大，故为探讨纱疵对气流牵引特性的影响，本文将重点探究短粗节纱疵。

结合纱疵形状特征及纺织工艺，一般情况下，纱疵在流体作用下迎流面以钝体状呈现，因此，根据文献[8]理论，可近似将纱线的短粗节纱疵看作球体或圆柱体，气流作用情形如图2所示。对于球体，可通过其直径ds来划分等级；对于圆柱体，可通过其直径dc和长度lc来划分等级，参照文献[8]根据长度与直径比对圆柱体阻力系数的研究，取lc/dc分别为2、4、8，可将每个等级划分成3种。假设纱线的平均直径为d，根据文献[3]对纱疵的分级，将纱疵截面增量界值定为+100%、+150%、+250%、+400%。本文研究以线密度为36.9 tex的纯涤纶纱为主要对象，通过金相显微镜测得纱线的平均直径d为0.29 mm，按照球体和圆柱体截面直径相对于纱线平均直径的百分比，计算出球体和圆柱体的直径界值为0.58、0.73、1.02、1.45 mm。

图2 气流作用情形Fig.2 Action of airflow on spheres (a) and cylinders(b)

2 纱疵阻力的数值计算

嵌入流体中的物体受到的牵引力F(对流体而言即为阻力)与流体的密度ρ、流体与物体的相对速度V、物体的迎流面积A和物体的牵引(阻)力系数CD相关，记为

对于静止于流场中的物体，式中的速度V即为流体的速度[8]。

为获得相对稳定的流场，依照文献[5]中的实验装置，即采用ZAX型喷气织机主喷嘴，在导纱管后面加辅助管道设计了一种纱线牵引力测试装置，并通过数值仿真发现在辅助管道中获得平稳的速度和密度，流体模型如图3所示。利用Fluent模拟可获得辅助管道中球体或圆柱体受到的气流速度及密度。以直径为1.5 mm的球体为例，当主喷嘴供气压为0.3 MPa时，其受到气流作用的速度如图4所示。边界条件参数的设定参照文献[6]中列出的数据值，计算获得每个节点的速度和密度，考虑边界层厚度，采用取平均值的方法获得气流作用球体和圆柱体的速度及密度。

图3 流体模型Fig.3 Fluid model

图4 球体速度等高线图Fig.4 Contour map of velocity in flow field with sphere

球体的阻力系数CD取决于雷诺数Re[9]

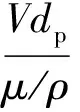
式中：dp为辅助管道直径；μ为空气黏度。因此有

根据Fluent数值模拟可获得密度ρ和速度V，气流的动力学黏度为1.79×10-5，根据雷诺数计算公式可知，辅助管道中雷诺数大于104，因此，计算阻力时取阻力系数CD为0.44。圆柱体的阻力系数CD取决于雷诺数和其长度与直径之比，当雷诺数大于104时，根据文献[8]，lc/dc为2、4、8时分别可取牵引力系数CD为0.85、0.87、0.99，计算得到球体和圆柱体受到的牵引力大小如表1所示。

表1 不同纱疵尺寸牵引力大小Tab.1 Drag force for different sizes of yarn faults

由计算的结果可知，对于短粗节纱疵，当纱疵相对于纱线平均直径越大，疵点受到气流的牵引力也就越大，对引纬过程中纱线受到的牵引力影响也越明显。

3 实验验证

注：A—采集仪；B—四合一放大器；C—动态电阻应变仪； D—计算机设备；E—张力仪；F—主喷嘴；G—辅助管道。图5 实验装置Fig.5 Experimental setup. (a) Experimental global graph; (b) Local view of auxiliary pipe

实验测试装置如图5所示。其中气路控制部分包括螺杆式空气压缩机、储气罐、过滤器、冷冻干燥机等[5]。纱线一端直接固定，另一端悬挂砝码，使纱线存在预张力，如图5(b)所示。通过悬挂不同质量(分别为5、10、20、50、100 g)的砝码重新标定拟合出纱线牵引力和微应变(x)之间的关系为F=1.632 89x。与数值仿真的辅助管道一致，选取有效长度为250 mm、直径为8 mm、主喷嘴在0.3 MPa供气压下，测得原始纱线的牵引力为0.4 733 N。置于辅助管道中的含固定球体纱线如图6所示，实验框架图如图7所示。

图6 含固定球体纱线Fig.6 Yarn with fixed spheres

图7 实验框架示意图Fig.7 Schematic of experimental test

按图6示意，将3个球体固定于纱线上，根据球体直径2、3、4 mm将实验分为3组进行测试，测得3组含有球体的纱线应变值分别为0.317、0.344和0.385，根据纱线牵引力和微应变之间标定的系数以及原始纱线受到的牵引力，即可计算出每个球体受到的平均牵引力，并与数值计算结果进行比较，结果如表2所示。当球体直径为2 mm时，由于不能得

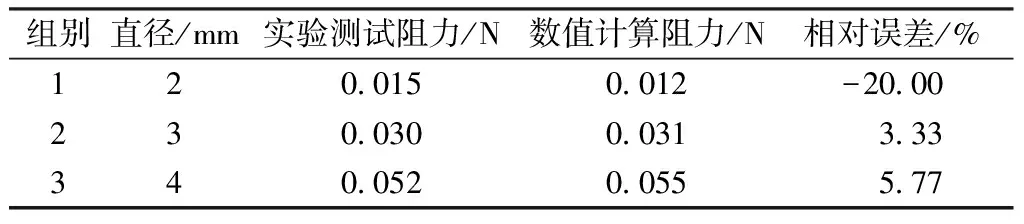
表2 数值计算与实验测试对比Fig.2 Comparison between numerical calculation and experimental test

到足够大的球体与纱线的直径比，导致有较大误差，不过可发现二者间有较好的一致性，从而可认为前述理论与数值计算具有较好的合理性。

4 短粗节纱疵对气流牵引特性影响

基于上述实验测试和数值模拟间较好的一致性，以球体模型化短粗节纱疵，进一步探究短粗节纱疵对气流牵引纱线特性的影响。纱线的牵引力公式[10]将含有球体的纱线受到牵引力分解成纱线受到的牵引力F0和球体受到的牵引力F′，即

由上式可知，牵引力由气流特性和纱线特性共同决定，其中气流特性由气流密度ρ和气流速度V组成，纱线特性采用纱线直径d、纱线长度l进行描述，牵引力特征以纱线牵引力系数CD作为比值参数呈现。由于辅助管道作为一维流场，流动特性比较稳定，可知球体通过改变d和CD来影响牵引力的大小。

取长为△l的纱线，在主喷射流作用下通过实验测试得到其牵引力为△F0，辅助管道中的气流相对平稳，可取△l纱线对应的ρV2的平均值(Fluent数值模拟)。当球体的直径与纱线平均直径d相等时，球体所受到的气流牵引力为0。而当球体直径大于d时，球体所受牵引力由牵引力公式计算，其中CD取0.44[9]。若对于纱线含有n个球体，每个球体都对应其气流参数，即可将含有纱疵的纱线牵引力系数表示为

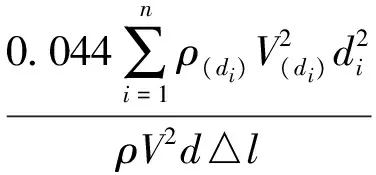
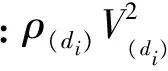
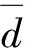
通过上述假设，将牵引力系数CD简化为仅与球体数量和球体大小相关的关系式：

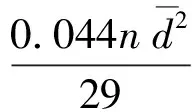
上式表明，当球体间距较大时，阻力系数与球的数量、球体迎流面积成正比，这从理论层面进一步说明纱疵的数量与大小对气流牵引力的影响。

为直观地比较随着球体直径、数量改变对纱线牵引力系数的影响，通过定义变化率来反映影响程度的大小。变化率定义为

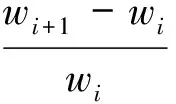
式中，wi为纱线牵引力系数随球体直径增加第i次或数量增加第i次的值。

初始时假设球体直径等于纱线直径，并定义r为球体直径与纱线直径d的比，即初始时r为1，设r以公差0.5增加，则可得到相应球体大小，假设球体直径不超过2 mm，并设球体数量为10，可得到纱线牵引力系数随球体直径增加变化率如图8(a)所示。初始时设球体数量为1，假设球体直径为0.5 mm，可得到纱线牵引力系数随着球体数量增加的变化率如图8(b)所示。

图8 球体对纱线牵引特性影响Fig.8 Influence of spheres diameter (a) and number (b) on drag force of yarn

从图8可看出，随着球体直径增大，纱线牵引力系数的变化率呈现逐渐上升并趋于平缓状态；而随着球体数量的增多，牵引力系数的变化率呈逐次下降态势。

5 结 语

基于纱疵在流体作用下迎流面以钝体状呈现现象，结合流体力学理论，提出将纱线局部纱疵模型化为球体和圆柱体理念，重点以短粗节纱疵为研究对象，结合理论分析方法与数值计算，对气流牵引含短粗节纱疵纱线进行了数值模拟，并通过实验进行了测试，对理论分析与数值模拟的合理性进行了验证，取得了较好的一致性，而进一步分析所得的牵引力系数简化模型对气流引纬的深入探究不仅有一定的理论研究意义，同样也有较强的工程应用价值。

FZXB

[1] 袁汝旺．纱线条干均匀度检测方法基础研究[D]．天津：天津工业大学，2014：5-16．

YUAN Ruwang．Yarn evenness based detection method[D]．Tianjin：Tianjin Polytechnic University，2014： 5-16．

[2] 迟开龙，潘如如，刘基宏，等．基于数字图像处理的纱线条干均匀度检测初探[J]．纺织学报，2012，33(12)：19-24．

CHI Kailong，PAN Ruru，LIU Jihong，et al．Primary discussion on detection of yarn evenness based on digital image processing [J]．Journal of Textile Research，2012， 33(12)：19-24．

[3] 王学元．纱疵分析与控制实践[M]．北京：中国纺织出版社，2011：39-42．

WANG Xueyuan．Analysis of Yarn Faults and Control Practice [M]．Beijing：China Textile & Appareal Press，2011：39-42.

[4] CHANG Lingli，TANG Zhengxue，WANG Xungai．Effect of yarn hairiness on energy consumption in rotating a ring-spun yarn package[J]．Textile Research Journal，2003，73(11)：949-954.

[5] 张晓飞．气流引纬纱线阻力及阻力系数的研究[D]．苏州：苏州大学，2016：56-63．

ZHANG Xiaofei．Analysis of the drag force of yarn and the drag coefficient during weft insertion[D]．Suzhou：Soochow University，2016：56-63.

[6] 徐存强，冯志华，董腾中，等．气流引纬主喷嘴内气流速度与纬纱间摩擦因数的关系[J]．纺织学报，2013，33(11)：147-152．

XU Cunqiang，FENG Zhihua，DONG Tengzhong，et al．Relationship between friction coefficients of weft yarns and velocity of air-flow in main nozzle during weft insertion [J]. Journal of Textile Research，2013，33(11)：147-152．

[7] CHEN Liang，FENG Zhihua，DONG Tengzhong，et al．Numerical simulation of the internal flow field of a new main nozzle in an air-jet loom based on Fluent [J]．Textile Research Journal, 2015，85(15)：1590-1601.

[8] FRANK M. Fluid Mechanics [M]．5th ed．Rhode Island： University of Rhode Island，2004：476-486．

[9] 胡国明．颗粒系统的离散元素法分析仿真[M]．武汉：武汉理工大学出版社，2010：114-115．

HU Guoming．Analysis and Simulation of Granular System by Discrete Element Method[M]．Wuhan：Wuhan University of Technology Press，2010：114-115．

[10] 皮利平科B A．气流引纬[M]．曹瑞，译．北京：纺织工业出版社，1984：19．

PIRRIPINKER B A．Weft Insertion by Air-Flow[M]．CAO Rui，Translating．Beijing： Textile Industry Press，1984：19．

Analysisonairflowdragcharacteristicsofyarnwithyarnfaults

ZHANG Rong， FENG Zhihua， LU Qing, CHEN Xiaoming

(CollegeofMechanicalandElectricEngineering,SoochowUniversity,Suzhou,Jiangsu215021,China)

In order to study the influence of yarn faults on airflow drags yarn, an assumption simulating short slub yarn faults by spheres and cylinders was proposed firstly according to the shape feature of yarn faults in airflow. The drag force of short slub yarn faults were numerically calculated based on analysis on airflow results by Fluent. The drag forces of spheres as model of short slub yarn faults were tested by self-designed testing drag force device for main-nozzle air-jet weft insertion under 0.3 MPa inlet pressure. The rationality of numerical calculation of previous statement was verified, and the consistency was obtained. Finally, the influence of short slub yarn faults on drag coefficient was studied. It is found that the change rate for coefficient of drag force increases firstly then verges to stabilization gradually with the diameter of yarn faults increasing. In addition, the change rate for coefficient of drag force presents descending tendency gradually with increase of the quantity of yarn faults.

yarn; yarn fault; air drag; numerical calculation; coefficient of drag force

10.13475/j.fzxb.20160902706

TS 101.2

A

2016-09-18

2017-08-11

张荣(1991—)，男，硕士生。主要研究方向为新型纺织机械、机电子流动态行为及其控制。冯志华，通信作者，E-mail:zhfeng@suda.edu.cn。