超声波电机转速的PIDNN控制
朱宜家, 陈国光, 范 旭, 杨智杰, 白敦卓
(1.中北大学 机电工程学院,山西 太原 030051; 2.豫西工业集团有限公司,河南 南阳 473000)
超声波电机转速的PIDNN控制
朱宜家1, 陈国光1, 范 旭1, 杨智杰1, 白敦卓2
(1.中北大学机电工程学院,山西太原030051;2.豫西工业集团有限公司,河南南阳473000)
针对行波超声波电机运行过程中的较强时变性与非线性特征,引入了一种比例—积分—微分神经元网络(PIDNN)电机速度控制器。控制器网络融合了状态转换函数,具备动态映射能力,利用PID控制律先验知识确定权值初值,通过可变学习速度反传算法(VLBP)在线学习,使训练结果快速收敛,不易陷入局部极小,从而实现对超声波电机稳定快速的控制。采用参数变化电机模型对控制器进行仿真校验,仿真结果表明:方法具有较快的响应速度和较高的鲁棒性,能通过在线学习补偿电机运行过程中的非线性。
超声波电机; 比例—积分—微分神经网络; 可变学习速度反传算法; 速度控制
0 引 言
由于超声波电机[1~3]特殊的工作原理,其输出特性会随环境温度、摩擦损耗、驱动激励频率等因素变化呈现出严重的非线性与时变性,因此,难以建立其精确数学模型。常规控制方法很难在无精确模型前提下,保证对非线性与时变性较强对象的控制精度。所以,智能控制与自适应控制成为超声波电机控制研究的发展方向[4~6]。由舒怀林提出的比例—积分—微分神经网络(proportion integration differentiation neural network,PIDNN),创造性地将比例、积分、微分环节融入神经元网络中。其结构简单,形态固定,通过PID控制规律确定权重初值,使网络收敛速度快,不易陷入局部极小[7]。
本文引入了PIDNN控制器,实现对超声波电机速度的自学习控制,给出了控制器的结构与数学模型,改进了控制器学习算法,并对控制器控制效果进行了仿真校验。
1 超声波电机速度控制特性
电机在工作过程中表现出较强非线性,在控制中主要面对的问题包括:电机的非线性死区、频率非线性漂移[8]。
非线性死区主要出现在电压幅值控制电机转速的情况下。用电压幅值控制电机转速时,输入电压与电机转速呈线性正比曲线,但当电压幅值低于某一常数时,转子突然停止,电机停转;同样,在输入电压达到一定数值后,电机转速也存在阈值区域[8]。
超声波电机在不同工作情况下,会出现谐振频率非线性漂移。影响电机系统谐振频率因素十分复杂,定子振幅变化、负载力矩变化等均会造成定子与转子之间接触率变化,影响系统谐振频率。此外,摩擦损耗会造成系统发热,电机材料参数变化,使系统谐振频率随温度升高呈下降趋势。电机工作频率一般在系统谐振频率附近,谐振频率漂移直接影响电机的控制效果。在开环控制时,频率漂移会造成电机转速随时间下降,直到达到热平衡,转速下降趋缓;闭环控制时,则会造成电机转速抖动和静差[8,9]。
2 超声电机的PIDNN控制系统
为了克服电机的非线性对控制的影响,改善超声波电机控制特性,在控制领域中引入了人工智能控制方法,并逐渐成为实现电机精确控制的主要研究方向[5]。PIDNN是其中一种重要方法。PIDNN不需要精确的数学模型,本身具有强大的学习能力,能够逼近系统的非线性输入—输出关系。神经元中融入了状态转换函数,能够描述系统动态特性,较一般前向神经元有着更好的动态映射能力[7]。这使得PID神经网络能减少电机不确定性带来的负面影响,实现电机精确控制。
2.1 PIDNN结构形式
单变量PIDNN(single variable PIDNN,SPIDNN)是PIDNN的基本形式,由一个2×3×1的3层前向神经元网络构成。采用SPIDNN结构的控制系统原理如图1,输入层由2个神经元组成,分别以参考速度r、超声电机实际输出速度y作为输入;隐含层由3个神经元组成,分别融入了比例环节、积分环节以及微分环节;输出层仅有一个神经元,完成控制规律的综合与输出[5]。
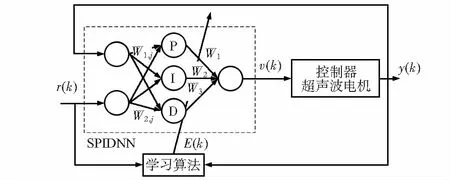
图1 SPIDNN 结构形式
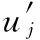
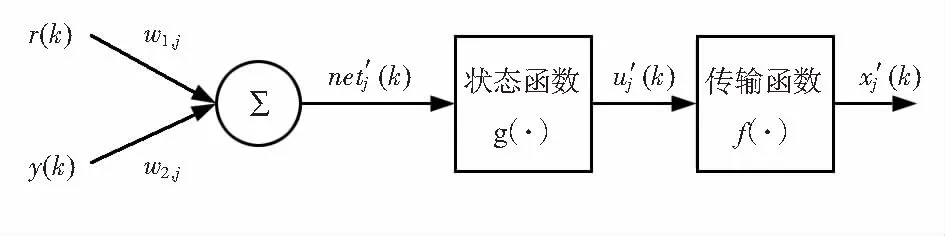
图2 单神经元结构
2.2 SPIDNN的前向算法[7]
1)输入层
在任意采样时刻k,输入层网络输入为
(1)
2)隐含层
隐含层由3个神经元组成,分别为比例元、积分元和微分元,其输入总值为

(2)
式中wi,j为输入层到隐含层的连接权重值。
比例元、积分元和微分元的状态和输出为
(3)
(4)
3)输出层
输出层包含一个神经元,完成网络的综合输出功能。其输出为
(5)
2.3 改进反向传播算法
1)批处理反向传播算法
PIDNN采用批处理反向传播(back propagation,BP)学习算法,调整网络中的权值。在整个训练集均提交网络后才更新参数,平均每个样本计算出的梯度,能有效减少迭代次数,得到更精确的梯度估计[8]。
在速度控制过程中,算法将调整网络中的权值参数,使式(6)目标函数最小化
(6)
根据近似均方误差的最速下降算法[4],可以得到隐含层到输出层权值更新

(7)
式中α2为学习步长;n为训练步数。根据微积分链法则可推导出变化梯度为
(8)
式中
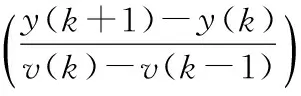
(9)
对于批处理训练网络电机输入对输出影响可被测量计算,其变化量为权重变化量的公因子,所以式(9)中采用输入—输出相对变化的方向表示∂y/∂v[5]。
对于输入层到隐含层,可得到其权值更新为
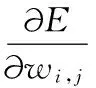
(10)
采用敏感度递推关系式[8],可以反向求得输入层到隐含层梯度变化
(11)
式中
(12)
2)带动量的可变学习速度反传算法
超声波电机工作中的非线性特征,使学习初始点相对位置与方向移动和变化,导致合适的学习步长难以选取:步长过小增加迭代次数,降低学习速度;步长过大造成一些工况下学习结果不收敛,影响系统稳定性。采用基础的BP算法难以获得较好的制效果。因此,本文引入可变学习速度BP(variable learning speed BP,VLBP)算法进行网络训练[8]。
引入动量项对权值更新公式进行改进
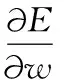
(13)
式中r为动量系数,为取值0~1。加入动量项后,相当于将权值更新从全量变化,变成了增量变化,每次权值变化量均与上一次变化量有关,有助于跳出局部极小值,加快收敛速度。在加入动量项的基础上引入VLBP法则。
VLBP算法学习规则如下:
a.若整个训练集上的均方误差在权值更新后增加,且超过了设置的百分数ζ(典型值为1 %~5 %),则权值更新被取消,学习速度乘以因子ρ,0<ρ<1,并且动量系数置0。
b.若均方误差在更新后减少,则权值更新被接受,学习速度乘以因子η>1。γ恢复原值。
c.若均方误差增长小于ζ,权值更新被接受,但保持原来的学习速度。γ恢复原值。
d.若权值更新后所得均方误差小于设定常数Emin,则停止学习。
在VLBP规则下,网络学习在性能曲面平缓处加速通过,在曲面斜率增加时减少学习速度,避免学习结果陷入局部极小。相对于一般BP算法,VLBP对初始训练步长要求低,对电机参数变化有更强的适应能力。
2.4 神经网络权值初值设定
为保证SPIDNN实现传统PID控制律特点,要使输入层至隐含层连接权值初值,完成由(r,y)→e的映射功能。所以,要求w1,j和w2,j大小相等方向相反,除此之外,为了保证调节过程中系统响应无静差,输入层至隐含层积分单元的权值和在整个过程中保持绝对值相等,符号相反,即|w1,2|=-|w2,2|。
3 仿真校验与分析
3.1 电机模型与控制系统参数给定
采用文献[10]中建立的,在空载情况下USR60超声电机及其驱动控制器辨识模型,即标称系统模型。综合文献[9,11]中实验数据,建立最坏情况模型。设定系统采样时间为0.1 ms,可得2个模型的离散系统差分方程为
y(k)=0.981y(k-1)+0.044 13v(k)+
0.043 8v(k-1)
(14)
y(k)=0.989y(k-1)+0.023 2v(k)+
0.023 11v(k-1)
(15)
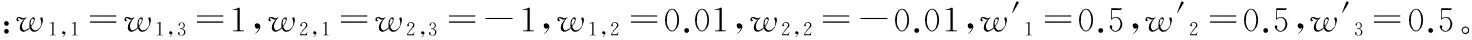
3.2 仿真结果
对PIDNN控制器的控制效果进行Matlab仿真。仿真中假设最坏参数情况发生在低速区,其余速度区间设为标称系统模型,并按照文献[12]中给出的参数变化规律,改变模型参数。
在3种典型输入下,改变初始情况下电机参数,并在控制过程中加入以下变化:恒定输入下,在速度稳态控制过程中使参数突变;跃变输入下,不同速度区间参数突变,低速区间参数进一步发生缓慢变化;正弦与余弦输入下,不同速度区间参数突变。然后,对控制系统进行50次和100次训练,得到优化后的控制效果。仿真结果如图3~图5(图中y为输出转速;r为参考速度)。图(a)为在电机参数突变后,在不同工况下对典型输入信号的跟踪效果;图(b)和图(c)为训练后的控制效果;图(d)为训练过程中目标函数变化曲线。
从图3~图5可以看出:电机参数变化后,系统对不同输入信号跟踪明显变坏,但经过一定步数在线学习,可以得到较为理想的控制效果。
在电机实际运行控制中,噪声、干扰等因素无法避免。所以,在输出信号中加入一定的白噪声,验证系统抗干扰能力。仿真结果如图6所示,可知在噪声的干扰下,系统控制效果受到一定影响:在中、高速区间,噪声的影响较小;在低速区间影响较大,其目标函数曲线出现了明显抖动。
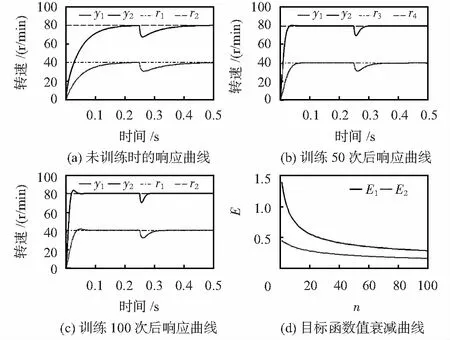
图3 恒定输入下响应曲线
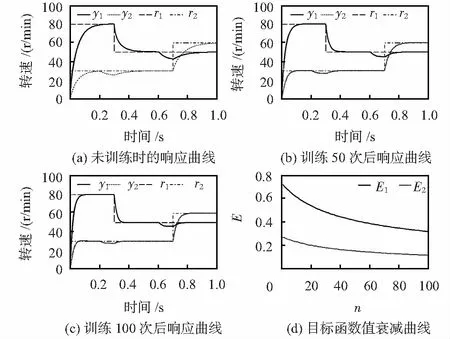
图4 跃变输入响应曲线
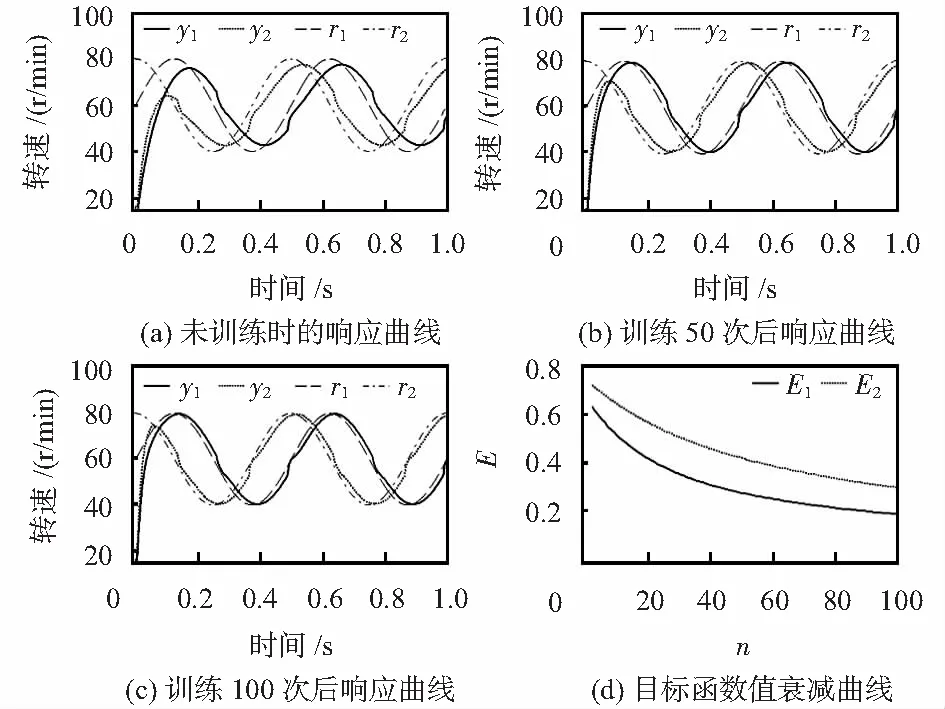
图5 正弦和余弦输入响应

图6 加入噪声的响应曲线
VLBP算法对系统学习性能有了一定的提高,如图7所示。但该方法本质上是BP算法的简单改进,也具有BP算法固有的缺陷,对系统性能提升不大。图中响应产生超调的原因与目标函数有关,改变目标函数可以获得不同控制效果。

图7 2种学习方法响应曲线对比
4 结 论
仿真结果表明:基于PIDNN的超声波电机控制器,能采用等效PID控制律原则,进行权值初值的设定,避免学习陷入局部极小,通过VLBP算法加快了学习的收敛速度,确保了控制系统稳定性。控制器通过在线学习,能够有效补偿电机运行过程的非线性,实现对速度的快速、稳定控制,改善了超声波电机速度控制性能。
[1] 史敬灼,吕方方,吕 琳.超声波电机运动控制技术的发展[J].微特电机,2011,39(5):76-78.
[2] 罗辞勇,卢 斌,张 帆,等.超声波电动机发展现状及应用[J].微特电机,2011,39(11):70-74.
[3] 贺红林,赵淳生.基于模型参考自适应技术的超声电机测控研究[J].传感器与微系统,2008,27(9):52-55.
[4] 张彩霞,史敬灼.超声波电机非线性自适应位置控制[J].微电机,2016,49(10):25-29.
[5] 王寿健,金 龙,徐志科.基于BP神经网络控制算法的超声波电动机控制[J].微特电机,2011,39(2):44-46,59.
[6] 王 健,孙志峻,郭 语,等.单超声机驱动两足行走机器人的设计分析研究[J].传感器与微系统,2010,29(6):11-13.
[7] 翟尧杰,舒怀林,熊胜祖.PID神经网络改进研究[J].机电工程技术,2010,39(8):39-41,115,199.
[8] 史敬灼,尤向阳.超声波电机转速特性仿真与神经网络建模实验研究[J].微电机,2009,42(9):18-21.
[9] 朱 华,贺红林,陈志华,等.超声电机测控系统的一种实现方法[J].传感器与微系统,2006,25(7):64-66.
[10] 雷伏容,钟宜生,徐文立.行波型超声马达的数学模型[J].压电与声光,2003,25(4):328-332.
[11] 马丁·哈根,霍华德·德穆斯,马克·比尔.神经网络设计[M].戴 葵,译.北京:机械工业出版社,2005:232-235.
[12] 张新良,谭永红.行波型超声电机基于输入电压变化的参数模型辨识[J].系统仿真学报,2008,20(13):3492-3495.
PIDNNrotatingspeedcontrolofultrasonicmotor
ZHU Yi-jia1, CHEN Guo-guang1, FAN Xu1, YANG Zhi-jie1, BAI Dun-zhuo2
(1.CollegeofMechanicalandElectricalEngineering,NorthUniversityofChina,Taiyuan030051,China;2.YuxiIndustrialGroupCompany,Nanyang473000,China)
Aiming at strong time-varying and non-linear characteristics in the process of ultrasonic motor operation,a motor speed proportion integration differentiation neural network(PIDNN)controller is introduced.The controller network fuses the state transition function,and uses the PID control law prior knowledge to determine the initial value of the weights.Through the variable learning speed BP(VLBP)algorithm,training results are quickly converged and it is difficult to fall into the local minimum,so as to stably and fastly control ultrasonic motor.Use parametric-variable motor model to simulate and verify controller.The simulation results show that the method has a fast response speed and high robustness, and can compensate the nonlinearity of the motor during operation by online learning.
ultrasonic motor; proportion integration differentiation neural network(PIDNN); variable learning speed BP (VLBP); speed control
10.13873/J.1000—9787(2017)11—0060—04
TP 273
A
1000—9787(2017)11—0060—04
2017—09—07
朱宜家(1991-),男,硕士研究生,主要研究方向为兵器科学与技术。

