基于多惯性传感器姿态的输电线舞动监测算法研究
朱勤翔, 郭 薇, 张 港
(上海交通大学 区域光纤通信网与新型光通信系统国家重点实验室,上海 201100)
基于多惯性传感器姿态的输电线舞动监测算法研究
朱勤翔, 郭 薇, 张 港
(上海交通大学区域光纤通信网与新型光通信系统国家重点实验室,上海201100)
针对目前使用惯性(MARG)传感器还原输电线舞动形状存在很多原理性的问题,如位置积分起始点未知、容易丢失输电线低频运动信息等,提出了一种基于惯性传感器姿态的输电线舞动形状还原算法,采用融合同一根输电线上多个MARG的姿态求取每个MARG真实位移以及输电线整体形状。算法能够避免加速度积分时的累积误差,解决了输电线长度约束问题且使用较少MARG即可还原舞动图像。仿真结果表明:算法可以有效地降低导线舞动振幅的误差,且还原误差不随时间增长。
惯性传感器; 姿态—曲线还原算法; 输电线舞动; 姿态
0 引 言
输电线在覆冰条件下受到强风的激励,容易产生一种自激的、低频、振幅巨大的无规则舞动,从而引起输电线脱皮、跳闸、断股、甚至拉倒杆塔等危害[1]。常用的基于加速度的舞动监测系统在一根输电线上绑定多个惯性传感器(MARG)并测量其加速度、地磁场以及角速度,然后对校正后的MARG加速度进行二次积分得到位移信息,最后通过插值得到整根输电线形状[2]。
该系统存在以下问题: 1)加速度积分过程中,初始速度值和位置值无法准确估计。2)在积分过程中,由于要解决噪声引起的积分不收敛,一般均需要加入滤波器消除噪声。而滤波器消除了真实的MARG的低频移动。因此,即使速度和位置的初始值足够准确,经过一段时间后系统仍然无法计算MARG的准确位移。3)由于每个MARG得到的位移均不够精确,综合这些位移拟合得到的输电线的整体形状与真实值有较大误差。4)刚体绕着某个轴做某个角度的旋转后得到的角度关系称为该刚体的姿态,监测系统需要计算MARG姿态以消除转动误差。在经典的姿态算法中一般需要加速度计、陀螺仪和磁力计三种传感器同时使用才能获得准确的姿态[3]。但在基于加速度的监测系统中加速度用于积分位移,因此,只能使用另外两者计算姿态[2],最终会导致校正过的加速度仍然不准确。
针对上述问题,本文提出了一种新的基于传感器姿态的输电线舞动监测系统及姿态—曲线还原算法。算法舍弃了加速度积分的原理,通过计算绑定在输电线上的MARG的姿态,再结合MARG的绑定位置得到整根输电线的形状。仿真及实验结果表明:本文方法能够很好地避免现有系统的缺陷,并且可以有效地提高还原的位移精度,从而获得较为精确的整体输电线舞动形状。
1 基于姿态舞动监测系统及还原算法
1.1 基于姿态舞动监测系统
图1所示,多个MARG测量单元绑定于同一根输电线:两端各绑定一个MARG,其余以等间隔绑定在输电线中央。每个MARG内含有加速度计、磁力计和陀螺仪用于测量其姿态。基于姿态的监测系统与现有基于加速度的监测系统硬件结构相同,包括带有无线传输功能的MARG、监测基站以及远程控制中心[4]。基于姿态的舞动监测系统的数据处理流程为:接收MARG的测量数据后,系统首先使用姿态算法计算MARG的实时姿态[3,5],其次使用姿态—曲线还原算法得到整根输电线形状,最后计算其他舞动参数,如舞动频率等。
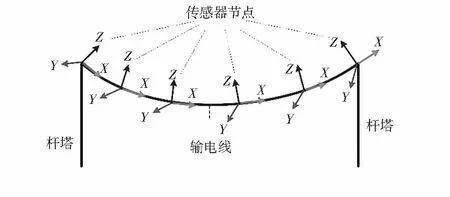
图1 基于姿态舞动监测系统示意
1.2 姿态曲线还原算法
1.2.1 建立输电线方程
姿态—曲线还原算法使用MARG实时姿态作为输入,并通过其计算整根输电线的实时形状。根据MARG的姿态可以计算绑定点输电线的切线方向,且相邻MARG之间的输电线长度为一个已知的常数。姿态—曲线还原算法中用于描述输电线的曲线方程必须具有以下4个性质:
1)连续性约束:曲线必须处处连续,在绑定MARG的“测量点”上也必须连续。
2)首尾位置约束:曲线的起点和终点必须和输电线的首尾两端的坐标相同。
3)切线约束:曲线在测量点上的切线方向必须与实际MARG测量的切线方向相同。
4)弧长约束:该曲线在相邻测量点间的曲线长度必须等于原输电线在对应测量点间的弧长。
为满足上述4个约束,姿态—曲线还原算法使用空间曲线r(t)=(x(t),y(t),z(t))作为描述输电线的方程[6,7]。该曲线的导数r′(t)=(x′(t),y′(t),z′(t))等于某个二次函数σ(t)(空间曲线的速度)
x′2(t)+y′2(t)+z′2(t)=σ2(t)
(1)
该曲线的导数有另外一种等价的复数形式[6]
r′(t)=(|α(t)|2-|β(t)|2,
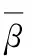
(2)
σ(t)=|α(t)|2+|β(t)|2
(3)

为了满足MARG所处测量点的切线约束以及弧长约束,姿态—曲线算法对每一段被测量点分割的输电线均使用独立曲线表示。具体地,如果一条输电线上绑定了n+1个MARG,那么该输电线将被分成n段,姿态—曲线还原算法使用n段曲线来表示各段输电线。而每一段的曲线方程ri(t)的α(t),β(t) 系数表示为
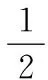
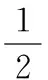
(4)
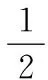
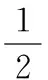
(5)
式中 (pi,qi),i=0,…,N+1为n+2组复数常数;t的取值范围为t∈[0,1]。由上文中4个约束知曲线簇必须满足约束方程
ri(1)=ri+1(0),i=1,…,N-1
(6)
(7)
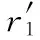
i=1,…,N-1
(8)
(9)
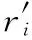
1.2.2 求解输电线模型方程
根据式(2)、式(4)、式(5)确定(pi,qi)后,曲线簇可以被唯一确定。本节将说明姿态—曲线算法如何计算复数(pi,qi)使之满足4个约束,式(2)~式(5)结合约束式(6)~式(9)得到式(10)~式(14)
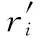
(10)
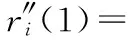
(11)
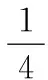
(12)

(13)
(14)

|qi-1-2qi+qi+1|2)
(15)
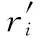
切线约束:式(10)中计算的切线应当满足实际MARG计算得到的切线di=(dxi,dyi,dzi),i=0,…,N,得到式(12)。
弧长约束:式(13)计算了每一段曲线的长度,应该等于实测值li。将式(4)、式(5)代入式(13),可将每段曲线的长度li用复数对(pi,qi)表示。
首尾位置约束:设该输电线首尾两端相对距离Δd=(Δx,Δy,Δz)。将式(2)代入约束方程(7)得到式(14),式(14)也可以用复数对(pi,qi)表示。
目前,四个约束(式(6)~式(9))均能由复数对(pi,qi)表示,式(12)~式(14)共包含了4N+6个标量方程,复数对(pi,qi)中共含4N+8个变量,故姿态—曲线还原算法使用最小化函数式(15)的方法确定(pi,qi)。式(15)可理解为五次曲线到三次曲线的“距离”,描述了输电线的平滑性,值越小输电线越平滑。使用现有的最优化方法求解最小化函数式(15)[8]。最优化计算中,与真值接近的初始值(pi,qi)init可降低姿态—曲线还原算法的运行时间。在姿态—曲线还原算法中,每一个时刻的初值(pi,qi)init设置为上个时刻得到的最优值(pi,qi)optimal。关于初始时刻的最优化初值,可以使用表示输电线静止时的(pi,qi)stabie作为初值。
2 仿真实验
使用Matlab作为仿真环境,对比基于加速度的监测系统和基于姿态的监测系统在两种输电线舞动模式下的还原效果:1)最简单的摆动模型;2)来自于对真实输电线舞动的有限元模拟数据[9],该模式下输电线做无规则运动。文中对比实验中,基于加速度的舞动还原系统的初始位置均为零时刻位置。
2.1 输电线摆动模式舞动还原
该模式下,输电线在无风静止呈垂链线状,开始舞动时输电线上各点多作类单摆运动,运动平面垂直于输电线方向,同时输电线会沿其切线方向做扭转运动。监测系统于输电线绑定了5个MARG。
图2对比了位于输电线中点的MARG的位移图像。在这种舞动模式下,两种系统的还原结果均较准确。这种模式中由于该MARG运动中心并未发生变化,因此,基于加速度系统的劣势并不明显。图2(a)中,基于加速度系统的结果在X轴上有近0.3m的运动,这是由于该系统计算姿态不够准确所致。基于姿态的还原系统不仅能得到绝对的位移,并且在位移幅度和位移平面上也与真实值非常相近。

图2 MARG位移还原(摆动模型)
图3对比了某个时刻两种监测系统对输电线整体形状还原效果。两者均较为准确地获得正确的输电线形状。
2.2 有限元模拟输电线舞动数据还原
现实中,输电线做不规则舞动,监测该输电线使用6只传感器。图4对比了某个MARG的位移图像,图中基于姿态系统的还原结果与真实值非常相似,而基于加速度系统与真实值相差较远。这是由于基于加速度的系统无法测量MARG的低频运动,而基于姿态的系统因为可获得绝对位置,故还原效果更准确。

图3 输电线还原(简单模型)
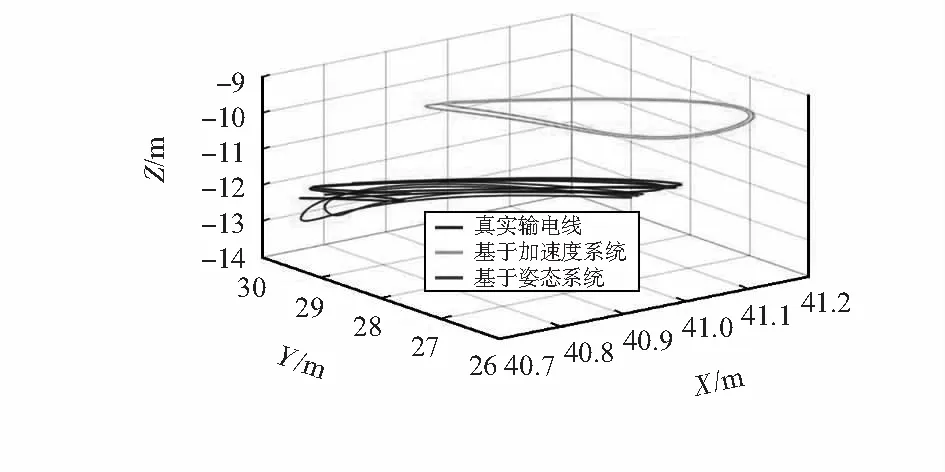
图4 MARG位移还原(有限元设计模型)
图5为某个时刻两种监测系统还原整根输电线的效果。基于加速度的系统只能获得相对位置,当MARG运动中心变化后该系统无法获得准确的采样点位置,导致最终还原结果错误。基于姿态的监测系统则仍然能准确地获得输电线的实时舞动形状。
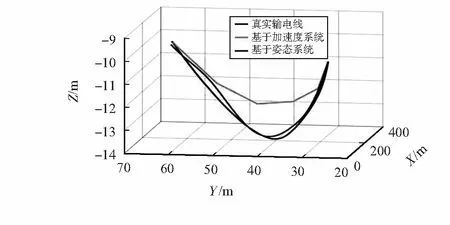
图5 输电线还原(有限元设计模型)
3 结束语
针对现有的输电线监测系统所存在的4个缺陷,提出了姿态—曲线还原算法,主要原理是通过MARG的姿态计算输电线的舞动形状,并代替了现有的基于加速度积分的算法。在硬件架构上,基于姿态的舞动监测系统与现有系统完全相同,因此,姿态—曲线还原算法可以直接应用到现有的舞动监测系统中,并得到更为准确的结果。使用本算法的优势在于能够获得绝对位置、位移幅度更精确并且可以获得整根输电线的舞动形状。
[1] 王少华,蒋兴良,孙才新.输电线路导线舞动的国内外研究现状[J] 高电压技术,2005,31(10):11-14.
[2] Lü Zhongbin,Li Qing,Ni Yiqing,et al.An efficient method for galloping profile monitoring of power transmission lines by use of an inertial unit:Theoretical and experimental investigation[C]∥Advances in Structural Engineering and Mechanics,Korea:Incheon,2015:22-29.
[3] Crassidis J L,Markley F L.Unscented filtering for spacecraft attitude estimation[J].Journal of Guidance,Control,and Dynamics,2003,26(4):536-542.
[4] Xie K,Zhang C,Li Q,et al.Tracking galloping profile of transmission lines using wireless inertial measurement units[J].Journal of Computer and Communications,2015,3(5):220.
[5] Trawny Nikolas.Indirect Kalman filter for 3D attitude estima-tion[J].Twin Cities,Minnesota:University of Minnesota,2005.
[6] Farouki Rida T.Pythagorean hodograph curves[M].Berlin Heidelberg:Springer,2008.
[7] Huard Mathieu.C2 interpolation of spatial data subject to arc-length constraints using pythagorean hodograph quintic splines[J].Graphical Models,2014,76(1):30-42.
[8] 陈宝林.最优化理论与算法[M].北京:清华大学出版社,2005.
[9] Hu J C,Song Z,Ma J G.Model for comprehensive simulation of overhead high voltage power transmission line galloping and protection[C]∥IEEE Conference on Electrical Insulation and Dielectric Phenomena,IEEE,2006:190-193.
ResearchonpowertransmissionlinegallopingmonitoringalgorithmbasedonmultipleMARGsensorattitude
ZHU Qin-xiang, GUO Wei, ZHANG Gang
(StateKeyLaboratoryofAdvancedOpticalCommunicationSystemsandNetworks,ShanghaiJiaoTongUniversity,Shanghai201100,China)
Monitoring the motion of power transmission line(PTL)through magnetic angular rate and gravity (MARG) sensor array,including accelerometer, magnetometer and gyroscope,is one of the most mature technology in PTL monitoring system.However,it suffers lot of principle problems,such as initial point of position integration is unknown and the low frequency movement information of PTL is easy to be lost.Propose a new attitude-based algorithm to estimate real-time movement of PTL during galloping: it fuses the attitudes of multiple MARG sensor deployed on the PTL to calculate the displacement of MARG sensor as well as the movement of PTL.With this algorithm,integration cumulative error in displacements can be avoided,solve length constraints of PTL and recover PTL galloping movement image accurately through just a small number of MARG sensor.Simulations prove that this algorithm can reduce amplitude error of PTL galloping,and restoring error can′t increase with time.
magnetic angular rate and gravity(MARG)sensor; attitude-curve recovery algorithm; power transmission line(PTL)galloping; attitude
10.13873/J.1000—9787(2017)11—0021—04
TP 212
A
1000—9787(2017)11—0021—04
2016—11—09
朱勤翔(1989-),男,硕士,主要从事基于MARG的导航定位方面及输电线舞动监测方面的研究工作。

