轮毂轴承性能试验中泥浆搅拌数值模拟及研究

，，， ， ，

(1.浙江工业大学 机械工程学院，浙江 杭州 310014；2.浙江万向精工有限公司,浙江 杭州 311202)

轮毂轴承性能试验中泥浆搅拌数值模拟及研究

翁泽宇1，关慈明1，黄德杰2，汪峰2，翁聪1，桂元坤1

(1.浙江工业大学 机械工程学院，浙江 杭州 310014；2.浙江万向精工有限公司,浙江 杭州 311202)

掌握泥浆搅拌装置设计的关键技术，依赖于泥浆搅拌过程的研究.在对两相流有限元计算方法和模型展开讨论的基础上，基于欧拉-欧拉方法的Eulerian模型，利用Fluent流体仿真软件，实现了汽车轮毂轴承性能试验中泥浆搅拌过程的数值模拟.通过模拟得到的泥浆固相颗粒分布云图，研究搅拌槽的浓度分布和均匀性.提出了泥浆搅拌装置功能设计的基本要求，研究了泥浆固相颗粒在搅拌槽底部的完全离底悬浮问题和取浆口的设置问题.相关技术已用于指导泥浆搅拌装置的设计.

泥浆；搅拌过程；数值模拟；轮毂轴承

汽车轮毂轴承性能试验中，泥浆是一种十分重要的环境介质，泥浆搅拌装置是环境模拟试验系统的重要组成部分.但是，由于缺乏对泥浆搅拌装置的研究，不符合要求的泥浆搅拌装置将使得汽车轮毂轴承性能试验的有效性很难得到保障，泥浆搅拌装置的设计已经成为了业内的技术瓶颈.汽车轮毂轴承性能试验所用泥浆是由多种成分组成的混合物，除了添加有一定量的不可溶的固体颗粒外，还添加了氯化钠、氯化钙等可溶性物质.泥浆的配比和均匀性直接影响到汽车轮毂轴承性能试验的结果，泥浆的搅拌是影响泥浆的配比和均匀性最重要的影响因素.而且，如果搅拌不当，还会使泥浆在底部长期堆积产生粘连.所以固体颗粒分布问题是泥浆搅拌过程研究的主要内容.泥浆搅拌过程中的固体颗粒分布问题属于液-固悬浮问题，目前对于此类问题主要是采用经验公式进行理论估算，由于经验公式对影响因素的描述比较简单，对一些复杂工程问题，存在较大的误差.计算流体数值模拟技术的发展，为分析计算此类复杂的工程问题创造了条件.对于此种问题可以基于计算流体力学中欧拉-拉格朗日方法和欧拉-欧拉方法进行两相流的有限元计算，可进行此类计算的有限元仿真软件有Fluent，CFX，Star-CD等.目前已有国内外学者关于搅拌问题数值模拟研究的报道，并取得了与实验较高的吻合度.Zadghaffari等[1]利用数值模拟方法对搅拌装置进行了计算，得到了混合时间与功率.Micale等[2]利用数值模拟方法对搅拌装置进行仿真，获得了低浓度固体颗粒的分布规律.ALWAYS等[3]利用数值模拟方法对不同直径固相颗粒分布进行了研究，指出固相颗粒直径越小，在搅拌装置内越趋于均匀.钟丽[4]利用数值模拟方法研究了石英砂-水两相物系固体颗粒离底悬浮的判据.在石油化工领域，庞向飞等[5]利用数值模拟方法对PY型桨叶尺寸、离底高度和转速等对流场分布的影响进行了分析.但是，目前笔者所涉及的泥浆搅拌过程的数值模拟及研究还没有相关的报道.泥浆的固体颗粒粒径较小，属于粉体类型，而且分布范围不宽，使用数值模拟的手段研究泥浆搅拌装置是非常有价值的一种探索.

为了保证轮毂轴承性能试验中泥浆配比的准确性，笔者针对泥浆搅拌装置的颗粒分布问题，采用欧拉-欧拉方法，通过Fluent软件对泥浆搅拌过程进行数值模拟，获得泥浆搅拌过程的流场分布和颗粒分布，进而对泥浆搅拌装置的完全离底悬浮转速、取浆口位置的设置问题进行研究.

1 物理模型与数值模拟方法

如图1所示，泥浆搅拌装置由圆柱形搅拌槽、桨式桨叶和转轴组成.搅拌槽直径D为500 mm，高度H为340 mm；桨叶长T为220 mm，宽度b为60 mm，厚度ε为2 mm；桨叶离底高度h为125 mm，转轴d直径为16 mm.研究的物系为亚利桑那粉-水两相体系，固相密度为2 650 kg/m3，固相体积分数为10%.

由于三维模型属于旋转机械的流场仿真，根据流场的对称性，取槽体的1/2进行网格划分，采用非结构化网格进行划分，网格数为409 502个.

图1 搅拌装置结构示意图Fig.1 The structural diagram of mixing tank

1.1 数值模拟方法

泥浆搅拌装置搅拌的数值模拟涉及到内流场模拟，液-固两相拥有各自不同的特性又会产生相互作用，是一个相对复杂的过程，需要选取合适的模型进行仿真，其中涉及到两相流模型、湍流模型和曳力模型等的选择.

1.1.1 两相流模型

泥浆搅拌装置的液-固悬浮属于两相流问题，在Fluent中对于两相流可以采用基于欧拉-欧拉方法的三种模型：Eulerian模型、混合模型和VOF模型.此类模型的特点是把弥散颗粒相和连续流体相一样视为连续介质，运用类似于连续介质的处理方法来处理颗粒相，将颗粒相视为欧拉坐标系中与连续相相互渗透的一种“假象”流体，称为拟流体.因此，这种模型又叫做颗粒模拟流体模型.

1) Eulerian模型：可用于气-液-固任意相组合的模拟，各相可以是分离的或相互作用的，每一相均采用欧拉方法处理.各相模型的守恒方程与附加守恒方程组成了计算所需的多相流守恒方程.

2) 混合模型：可用于模拟存在相对运动速度的多相流[6]问题，主要有粒子沉降、旋风分离及小体积比的气泡流动等问题，通过求解混合相的质量守恒、动量守恒和能量守恒方程，以及第二相的体积分数方程来模拟各相流速不同的多相流，或耦合性很强的各向同性同流速的多相流.

3) VOF模型：适用于计算两相之间不能相互渗透的流体运动，主要应用于射流破碎、流体中气泡运动、气液界面[7]的稳态和瞬态模拟等问题，通过求解每一相体积分数的连续方程以及单独的动量方程和能量方程来模拟不能相互混合的流体的流动.

对于液-固两相悬浮问题，VOF模型不太适宜，混合模型与Eulerian模型皆可应用，但混合模型实质上是简化的Eulerian模型，计算速度较快但是精度较低，所以笔者选择Eulerian模型进行模拟.

1.1.2 湍流模型

湍流模型采用标准k—ε离散模型[8]，其适用于单一连续相为主相，其余为低体积分数的相，湍流动能k和湍流动能耗散率ε表达式为

(1)

(2)

(3)

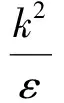
(4)

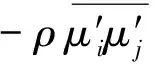
1.1.3 曳力模型

对液-固悬浮问题，需要考虑连续相作用于颗粒上的曳力，在固相体积分数小于20%的液-固体系中Wen-Yu模型比较适用，液-固两相动量交换系数Ksl计算模型为Wen-Yu模型[10]，其表达式为

(5)

(6)

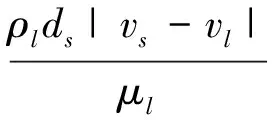
(7)

式中：ds为颗粒的直径，m；vs，vl为固相和液相的流速，m/s；αs，αl为固相和液相的体积分数；ρl为液相密度，kg/m3；μl为液相黏度，Pa·s.

1.1.4 其余设置

本数值模拟分析使用Syamlal&O’Brien碰撞黏度模型.近壁面区域流动计算采用标准壁面函数法.流场的计算使用MRF法，并设定流动性质为定常流动.通过对亚利桑那粉的粒径分析，这里假设固相的主要直径约为20 μm.相应的压力速度耦合选择SIMPLEC法，并采用一阶迎风的差分格式，计算残差取为1×10-4.

2 泥浆搅拌过程的数值模拟

泥浆搅拌装置在工作过程中，固相颗粒会受到液相流动产生的剪切力作用和自身重力等的作用力，在泥浆搅拌装置内各个位置的分布均不相同，通过对泥浆搅拌过程的数值模拟，可以得到其垂直与水平各个位置的固相体积分布图.

2.1 固相颗粒在垂直截面上的分布

图2是搅拌转速70 r/min，搅拌槽在0°，90°两个垂直截面的固相体积分布云图，从图2可以看出：固体颗粒分布在整个搅拌装置中，上部区域靠近顶部与转轴壁面的体积分数最小，下部区域靠近底面中心位置体积分数最大.

图2 垂直截面固相体积分布图Fig.2 Vertical sections volume fraction contours of particles

2.2 固相颗粒在水平截面上的分布

图3是搅拌转速70 r/min，搅拌槽内不同离底高度hf水平截面的固相体积分布云图，在不同高度上，固相颗粒的分布并不一致.

靠近搅拌槽底部位置，由于液相流场在中心部位作用较弱使得固相颗粒易集中于中心位置，中心固相体积分数较高，如图3(a，b)所示；在靠近桨叶部位时，由于液相流体的切向力作用，使得固相颗粒多分布与桨叶与搅拌装置壁面之间，平均体积分数较底部要低，也较为均匀，如图3(c，d)所示；在搅拌槽上半部分，由于液相流场在中心部位作用较弱，使得中心部位颗粒沉降速度更快，从而体积分数更小，平均体积分数较搅拌桨附近区域要低，均匀度也较好，如图3(e，f)所示.

图3 水平截面的固相体积分布图Fig.3 Horizontal sections volume fraction contours of particles

3 泥浆搅拌装置的研究

泥浆搅拌的目的在于，泥浆的固体颗粒与液相经搅拌混合后，在取浆口处使得泥浆配比达到使用规范.因此，泥浆搅拌装置功能设计的基本要求：1) 经搅拌，泥浆必须完全离底，使得搅拌槽底部无固相颗粒沉积，且转速不宜过高，避免增加功耗；2) 取浆口处的浓度均匀，且满足既定的泥浆配比要求.

3.1 固相体积分数分布

为了研究搅拌槽的泥浆颗粒分布与流场情况，分别取不同转速对搅拌过程进行仿真，得到各自转速下颗粒分布处于稳定状态时的分布图.图4是桨叶转速分别为30，70 r/min时的固体颗粒下的体积分数分布图.从图4中可以看出：搅拌装置底部较顶部浓度较高，30 r/min时搅拌装置上部会出现明显的清液层，但是随着转速的提升，随之而消失；而搅拌装置底部是整个系统中固相体积分数最高的地方，并且集中于中心部位，随转速上升，固体颗粒均随着主体流动而悬浮，而中心未悬浮体积缩小，整个系统的体积分布更加趋向于均匀.

图4 0°垂直截面固相体积分布图Fig.4 Volume fraction of 0° area distribution of particles

3.2 完全离底悬浮转速

目前，完全离底悬浮临界转速常用的判据是浓度判据和速度判据，但由于速度判据有一定的局限性，这里采用浓度判据判定完全离底悬浮转速.浓度判据[4]是使用单层球形颗粒的堆积体积分数来判定完全离底悬浮，若槽底局部颗粒堆积体积分数大于0.52，即认为有颗粒沉积现象，当槽底局部颗粒堆积体积分数小于0.52，则认为是固相颗粒完全离底悬浮.

对不同搅拌转速的泥浆搅拌过程进行数值模拟，所得的槽底最大体积分数结果作图5.由图5曲线可知：当转速为43 r/min时达到临界转速，即转速高于43 r/min时，搅拌槽中所有固相颗粒均已悬浮，不再会有颗粒堆积现象.

3.3 取浆口位置设置

取浆口位置设置基于Bohnet和Niesmak[11]的标准偏差模型，σ>0.8为非均匀悬浮体；σ在0.2～0.8为离底悬浮状态；σ<0.2为均匀悬浮状态.由于Fluent软件可以直接显示体积分数图，所以σ=0.1认为在标准偏差在此范围之内皆为符合泥浆配比要求，即固相体积分数为0.095～0.105.

图6，7是搅拌转速为50，70，80 r/min，搅拌槽在0°，90°两个垂直截面的泥浆均匀分布区域.由图6，7可见：均匀分布区域随着转速的提升而逐步扩大，在转速等于50 r/min时均匀分布区域主要分布在桨叶中心平面以下部位，此区域靠近槽底与桨叶，易带起颗粒团导致泥浆泵堵塞，不宜作为取浆口；转速增到70 r/min时，均匀分布区域明显扩大到桨叶以上的区域，除了靠近转轴与顶部液面外，其余位置均较为适宜作为取浆口位置；当转速增到80 r/min时，均匀区域继续扩大，但增速明显减缓.

图6 0°垂直截面均匀分布区域Fig.6 Vertical section of 0° area of uniform distribution

图7 90°垂直截面均匀分布区域Fig.7 Vertical section of 90° area of uniform distribution

4 结 论

采用基于欧拉-欧拉方法的Eulerian模型，可以实现轮毂轴承性能试验中泥浆搅拌过程的数值模拟.泥浆搅拌装置设计的关键是泥浆中的固相颗粒完全离底悬浮，取浆口处的泥浆浓度均匀，且满足既定的泥浆配比要求.泥浆搅拌过程的数值模拟，是研究泥浆搅拌装置技术关键的有效手段.泥浆搅拌装置设计的相关技术成果已经应用于开发汽车轮毂轴承单元单体密封试验机的开发，经实际运行使用，效果较好.

[1] ZADGHAFFARI R, MOGHADDAS J, REVSTEDT J. Study of flow field, power and mixing time in a two-phase stirred vessel with dual rushton impellers: experimental observation and cfd simulation[J]. Chemical product & process modeling, 2009, 4(1):3.

[2] MICALE G, MONTANTE G, GRISAFI F, et al. CFD simulation of particle distribution in stirred vessels[J]. Chemical engineering research & design,2000,78(3):435-444.

[3] ALTWAY A, SETYAWAN H, MARGONO, et al. Effect of particle size on simulation of three-dimensional solid dispersion in stirred tank[J]. Chemical engineering research & design,2001,79(8):1011-1016.

[4] 钟丽,黄雄斌,贾志刚.固-液搅拌槽内颗粒离底悬浮临界转速的CFD模拟[J].北京化工大学学报(自然科学版),2003,30(6):18-22.

[5] 庞向飞,梁红野,陈彦泽.直叶涡轮搅拌槽中流场的数值模拟[J].石油化工设备,2003,32(5):1-4.

[6] 张生昌,朱乐乐,马艺,等.气液两相流下单向球阀动态特性数值模拟[J].浙江工业大学学报,2016,44(1):1-4.

[7] 李相鹏,杨立军,李锋.气相F因子对规整填料内液膜流动的影响[J].浙江工业大学学报,2016,44(2):195-201.

[8] 童跃平,张淑佳,李贤华,等.标准k—ε模型与RSM模型在离心泵三维模拟中的比较[J].浙江工业大学学报,2008,36(6):678-681.

[9] 王福军.计算流体动力学分析[M].北京：清华大学出版社,2004.

[10] WEN C Y, YU Y H. Mechanics of fluidization[J]. Chemical engineering progress symposium series,1966,62:100-111.

[11] BOHNET M, NIESMAK G. Distribution of solids in stirred suspensions[J]. German chemical engineering,1980,3(1):57-65.

Numericalsimulationandresearchofmudmixinginthepropertytestofwheelhubbearing

WENG Zeyu1, GUAN Ciming1, HUANG Dejie2, WANG Feng2, WENG Cong1, GUI Yuankun1

(1.College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, China;2.Zhejiang Wanxiang Precision Industry Co., Ltd., Hangzhou 311202, China)

The research of mud mixing process is the key technology of mud mixing device design. Through the study of Two-Phase Flow finite element method and model, in the property test of wheel hub bearing, the numerical simulation of mud mixing process is realized by using fluent software based on Eulerian model and Euler-Euler method. The concentration distribution and uniformity of mixing tank are studied, by simulating the contours of mud particles distribution. Furthermore, the basic requirements of functional design in the mud mixing device are put forward, and the problems of complete suspension and the setting of mud particles outlet in the mixing tank are studied. Related techniques have been used to guide the design of mud mixing device.

mud; mixing process; numerical simulation; wheel hub bearing

2017-02-17

浙江省自然科学基金资助项目(Y1110994)；浙江省教育厅资助项目(Y200909905)

翁泽宇(1962—)，男，浙江杭州人，教授，研究方向为机械动力学及汽车零部件试验技术与装备，E-mail：wengzy8888@163.com.

U467.3

A

1006-4303(2017)06-0644-05

(责任编辑：陈石平)