基于能量损失理论的混凝土受压损伤本构模型
徐 娜,傅学怡
1) 广东科学技术职业学院建筑工程学院,广东珠海519090;2) 深圳大学土木工程学院,广东深圳518060

【土木建筑工程/ArchitectureandCivilEngineering】
基于能量损失理论的混凝土受压损伤本构模型
徐 娜1,傅学怡2
1) 广东科学技术职业学院建筑工程学院,广东珠海519090;2) 深圳大学土木工程学院,广东深圳518060
在Najar损伤理论基础上,基于《混凝土结构设计规范》(GB 50010—2010),提出一种新型的混凝土单轴受压损伤本构模型,得到混凝土单轴受压损伤的计算公式和演变方程,可更好地描述没有简化的混凝土单轴受压过程中的损伤状况. 给出常用强度等级的混凝土受压损伤本构曲线和损伤变量方程,对比分析不同强度等级混凝土的损伤曲线. 应用软件ABAQUS,建立一个矩形钢筋混凝土筒体剪力墙模型,绘制模型结构的极限承载力骨架曲线. 拟合对比分析,建立材料损伤和结构破坏的宏观近似关系,证明了假定是合理的. 该本构模型具有参数少、简单实用和精度较高等优点,利用此方法可以有效解决混凝土受压损伤的仿真分析.
混凝土;能量损失;Najar损伤理论;受压损伤;本构模型;损伤演变方程
在连续介质力学框架上建立起来的损伤力学中,损伤变量的概念包含在材料的本构关系内[1]. 损伤变量随着应力或应变的变化,被称为损伤的演化规律. 目前,混凝土的研究已广泛应用于损伤理论[2-7]. 其中,损伤理论包含能量损伤理论[8-12]和几何损伤理论[13-16].能量损伤理论的基础力学包括连续介质力学和热力学两方面,损伤过程被认为是能量不可逆的转换过程,损伤的本构方程和损伤的演变方程均通过耗散势能和自由能推导而来[17-18]. 基于能量的角度,损伤是一个不可逆的耗散过程[19-20]. 而建立损伤变量和消耗能量间的某种关系,作为提供解决混凝土受压损伤仿真分析的方法是有效合理的.
1 混凝土材料的损伤变量
基于能量损失的角度,研究混凝土的损伤情况. 在Najar损伤理论[21]中,脆性固体材料的损伤D可定义为
D=ΔWε/Wo
(1)
其中,Wo为应变能密度(无损材料),且
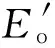
(2)

ΔWε=Wo-Wε
(3)
而
Wε=ε′:E:ε′
(4)
其中,E为损伤材料弹性系数的四阶张量.
2 Najar损伤理论
热力学过程即为混凝土受压力学的全过程,而能量的耗散过程或者不可逆的热力学过程即为其损伤的实质. 混凝土的受力状态如图1[21]所示. 其中,在应变逐渐到达ε的阶段,外力所做的功会转变为3种能量,包括弹性阶段的应变能量、塑性阶段的耗散能以及有关损伤的扩展能量. 在Najar损伤理论中,混凝土假定是无损伤的理想状态,直线OA代表了其应力-应变的关系,即σ=Eoε, 其中σ为应力值,那么外力在混凝土无损伤状态下所作的功为
ωperf=Eoε2/2
(5)
其中,Eo为混凝土初始弹性模量;ε为混凝土压应变.

图1 混凝土受力状态[21]Fig.1 The force of the concrete[21]
实际上,混凝土是处于有损伤的状态,图中OC段为应力和应变的关系曲线,那么在应变为ε时外力功ωPE为
ωPE=σε/2
(6)
损伤变量dc在Najar损伤理论中为


(7)
对混凝土这种损伤材料,它的应力下降现象在式(7)中得到了很好的诠释. 损伤变量方程是基于不可逆的能量耗散原理,无论是宏观上的力学性能还是微观上裂缝发展的整个下降过程,均得到了详细的诠释和表现,并且在混凝土结构的损伤研究中巧妙地绕开了研究混凝土的细微裂纹问题,大大简化了损伤研究的过程. 式(7)中,当结构处于理想状态时(无损伤),ωperf=ωPE,dc=0; 而对损伤的结构, 0≤ωPE≤ωperf, 且在极限状态下,即ωperf>>ωPE,dc→1,dc值在0~1之间.
3 受压损伤变量方程及其演变方程
实际上,直接应用Najar损伤理论使得混凝土的损伤程度得以量化是非常困难的,因为此时混凝土的损伤状态是基于宏观上的能量耗散. 因此,基于Najar损伤理论,本研究提出了一种新的混凝土单轴受压的损伤本构,从而更全面准确地诠释了《混凝土结构设计规范》(GB 50010—2010)[22]附录中混凝土单轴受压本构的损伤演变过程. 在该标准附录中混凝土单轴受压本构的基础上,本研究建立了损伤变量的表达式.
当处于无损伤状态时,σ=Eoε,f*c=Eoεo,即
(8)
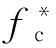
基于等价应变原理,可推出损伤材料的本构关系为
σ=E(1-D)ε
(9)
而假定损伤状态下,
(10)
所以
(11)

Najar损伤理论中
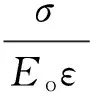
那么
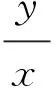
(12)
因此
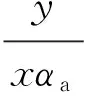
当0≤ε≤εo时,
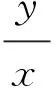
(13)
因此

当εo≤ε≤εcu时,
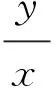
那么
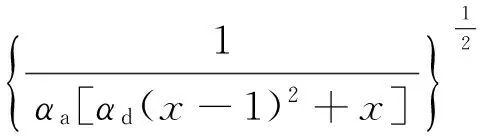

(14)
式(14)为混凝土的损伤变量方程.
在此基础上推导出混凝土损伤演化方程为
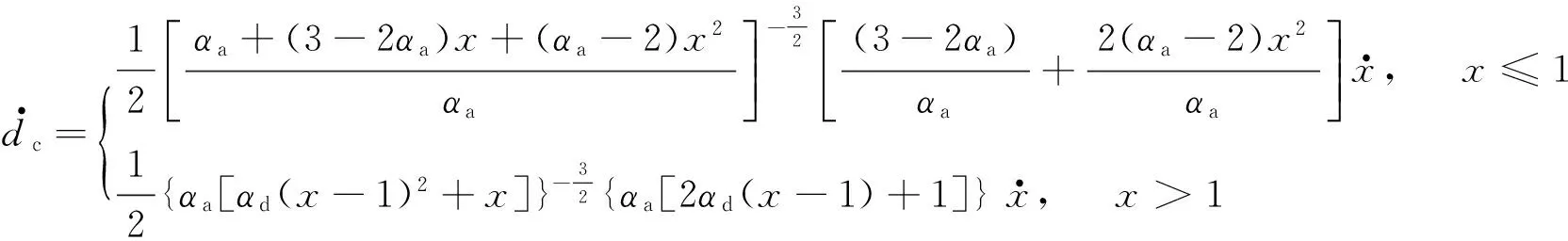
(15)
4 基于不同强度等级的混凝土受压损伤本构关系曲线
3种不同强度等级的混凝土本构关系模型参数见表1[23]. 3种不同强度等级的混凝土单轴受压损伤变量方程见表2. 在表2建立的混凝土损伤变量方程基础上,对比了3种不同强度等级混凝土的受压损伤变量和应变的关系,如图2. 从图2可见,在弹性阶段,混凝土无损伤;随着应变值进一步增大,混凝土进入塑性阶段,当损伤变量值陡然增大,曲线出现了第1个转折点;随着应变值继续增大,而损伤变量值缓慢增长,当曲线出现了第2个拐点时,损伤变量值基本保持不变,dc= 0.7. 此时,混凝土发生受压破坏,应变达到峰值压应变. 对比强度等级不同的混凝土,损伤变量值随着强度等级越低而越大,损伤越严重. 本研究混凝土单轴受压损伤本构模型与文献[24]中典型的混凝土损伤演变图基本一致.

表1 混凝土单轴受压应力-应变曲线的参数值[23]

表2 不同强度混凝土单向受压的损伤变量方程

图2 不同强度混凝土损伤-应变曲线Fig.2 Damage-strain curves of concrete under different strengths
5 受压损伤本构模型的应用
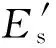
采用混凝土C35,考虑主要研究混凝土的受压破坏,简化其受拉应力应变关系,ft=fck/10, 且不考虑混凝土的受拉损伤. 采用本研究混凝土单轴受压塑性损伤模型,如图3.

图3 受压损伤变量-塑性应变曲线(C35)Fig.3 The relationship curve between compression damage variable and plastic strain(C35)

图4 底部截面应力分布图Fig.4 Stress distribution of bottom cross-section
首先在自重作用下的弹性范围内,分别查看结构底部截面应力、竖向位移及竖向反力,验证模型合理有效. 选取结构底部开洞墙体上的1个截面,该截面上节点1~7的应力值分别为0.760、0.717、0.675、0.674、0.674、0.716和0.759 N/mm2. 该截面的应力分布如图4. 由图4可知,应力集中发生在端部截面,随着应力不断向中间截面扩散,应力在中间位置逐渐达到均匀分布,且对称节点的应力基本相同,每层截面应力值基本相当.
该截面7个节点的竖向反力值分别为62.7、110.5、106.4、104.6、106.2、110.0和62.6 kN(图5),底部节点产生轴向反力,且应力集中发生在角部位置,此处竖向反力较小,中间截面竖向反力较大,截面对称的节点反力基本相同.
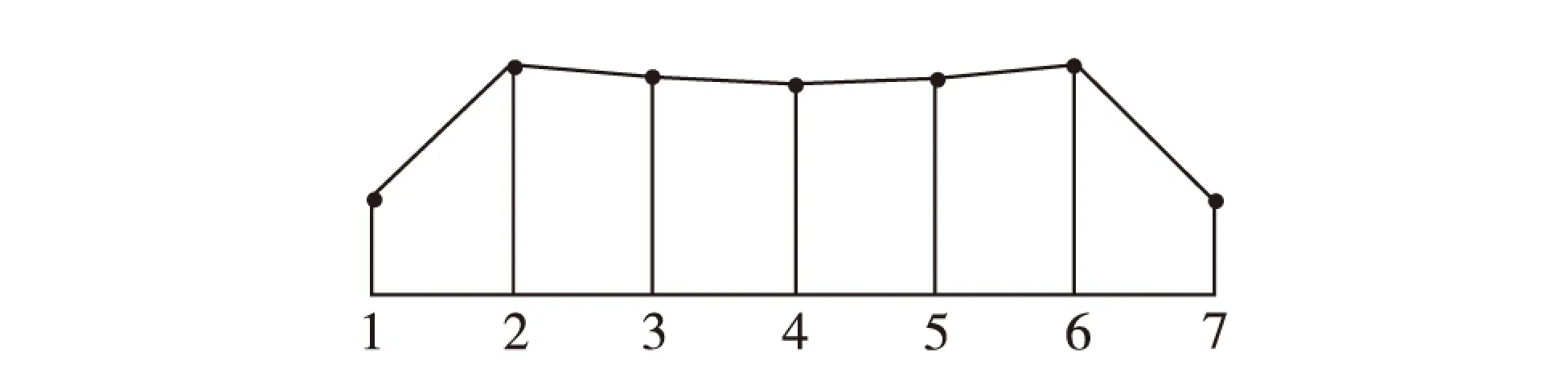
图5 反力分布图Fig.5 Reaction force distribution
该截面7个节点的竖向位移值均为0.34 mm,表明有限元数值模拟与理论相符,从而验证了模型合理可用.
应用该模型,进行弹塑性研究分析. 选取不同的组合,在模型上同时施加水平荷载和竖向荷载,即在保证轴力持续不变的情况下输入水平荷载.
在偏压构件处于正截面承载力极限状态时,其轴向的压力和弯矩是相互关联的. 利用Matlab软件按照下面的步骤编写Nu-Mu曲线的程序,以求得偏压作用下结构的极限承载力Nu-Mu理论的骨架曲线:
1)选取混凝土受压边缘的压应变为εcu;
2)选取受拉一侧的边缘应变;
3)基于混凝土单轴拉压本构模型、钢筋的单轴拉压本构模型以及截面的应变分布,得到混凝土的应力及拉压钢筋的应力;
4)压力Nu和弯矩Mu均根据平衡条件计得;
5)另外选取受拉一侧边缘应变,如图6所示,然后重复步骤3)和步骤4).

图6 计算简图Fig.6 Computing model
在实际情况中,当施加竖向荷载时,构件处于全截面受压状态,由于应力集中等原因,左右两端部截面出现假的损伤情况,所以我们不考虑端部截面的假损伤,只研究中部截面. 研究表明,此种情况下整个截面的受压损伤变量值均达到损伤的临界值,整个截面全部发生破坏. 当将水平荷载与竖向荷载同时施加于模型的时候,首先进入损伤状态的为右端截面,随着荷载的不断加大,损伤扩展,左端截面开始逐渐损伤. 研究偏压作用下所有组合的情况,损伤临界值均首先出现在截面的受压边缘.
假定当占整个截面7%的受压截面均达到损伤临界值时,结构定义为破坏,此时为极限承载状态,求得内力SFi. 处理求得的内力SFi数据,得到Nu-Mu组合,其中
假设受压为正方向,SFi对中间点取矩得到
Mu= SF2×a2+ SF3×a3+ SF4×a4+ SF5×a5+
SF6×a6+ SF7×a7+ SF8×a8+ SF9×a9+
SF10×a10+ SF11×a11+ SF12×a12+ SF13×
a13+ SF14×a14+ SF15×a15+ SF16×a16
(16)
其中,a2=3.5,a3=3.0,a4=2.5,a5=2.0,a6=1.5,a7=1.0,a8=0.5,a9=0,a10=0.5,a11=1.0,a12=1.5,a13=2.0,a14=2.5,a15=3.0,a16=3.5.
应用式(16),可求得实际偏压情况下结构轴力Nu和弯矩Mu的组合值. 再应用已有的绘制Nu-Mu骨架曲线的程序,可求得极限承载力理论骨架曲线. 对比研究分析求得轴力Nu和弯矩Mu的组合值与理论骨架曲线,如图7所示. 从图7可知,结构在偏心受压作用下发生破坏的所有情况均包含在该极限承载力骨架曲线中,其中混凝土受拉破坏为轴力为负值阶段. 我们只研究实际情况的受压破坏,包含大偏压和小偏压:
1)当弯矩为0时,轴力达到极限值;
2)当轴力为0时,弯矩没有达到极限值,弯矩是在发生界限破坏达到极限值;
3)在小偏压阶段,轴力随着弯矩的增大而减小;在大偏压阶段,轴力随着弯矩的增大而增大.
结构破坏均在此损伤程度下,且内力组合值与理论值曲线吻合较好,说明全截面的宏观破坏假定是合理的.

图7 Nu-Mu拟合对比Fig.7 Simulation and comparison of Nu-Mu
研究表明,无论混凝土强度等级为多少,当构件的7%的截面受压损伤值近于或超出受压损伤临界值,构件达到极限状态,发生破坏.
有别于以往的研究中判断结构是否破坏主要靠材料的微观性能,本研究基于理论的骨架曲线,在损伤和破坏之间建立了一种宏观的联系——当构件7%的截面受压损伤值接近或超出受压损伤临界值,构件达到极限状态,发生破坏.
结 语
基于Najar损伤理论,提出了一种新的混凝土单轴受压损伤本构模型,并在此基础上得出了混凝土单轴受压损伤的演化方程,绘制了典型强度等级的混凝土单轴受压损伤本构曲线. 建立了一个真实简单的剪力墙模型,并应用此混凝土单轴受压损伤本构模型,对比研究分析了模型的极限承载力骨架曲线. 此本构模型清晰全面地诠释了《混凝土结构设计规范》(GB 50010—2010)中混凝土的单轴受压本构关系,提供了混凝土单轴受压损伤应用的理论基础. 利用该数学模型,揭示了混凝土单轴受压损伤的本质及变化规律,提供了数据和参考给混凝土结构的损伤机理. 该本构模型具有参数少、公式简单、方法实用以及精度较高等优点,揭示了实际情况中材料的损伤程度和结构破坏的宏观关系.
引文:徐 娜,傅学怡. 基于能量损失理论的混凝土受压损伤本构模型[J]. 深圳大学学报理工版,2017,34(6):604-610.
/
[1] 余寿文,冯西桥. 损伤力学[M]. 北京:清华大学出版社,1997.
Yu Shouwen,Feng Xiqiao. Damage mechanics[M]. Beijing:Tsinghua University Press,1997.(in Chinese)
[2] 杨卫忠. 混凝土弹塑性随机损伤本构关系理论与试验研究[D]. 上海:同济大学,2007.
Yang Weizhong. Research on theory and experiment of concrete elastoplastic damage constitutive relation[D]. Shanghai:Tongji University,2007.(in Chinese)
[3] 何建涛,马怀发,陈厚群. 混凝土损伤本构理论研究综述[J]. 水利水电科技进展,2010,30 (3):89-94.
He Jiantao,Ma Huaifa,Chen Houqun. Summarize on the concrete damage constitutive theory research[J]. Advances in Science and Technology of Water Resources,2010,30(3):89-94.(in Chinese)
[4] 齐 虎,李云贵,吕西林. 基于能量的弹塑性损伤实用本构模型[J]. 工程力学,2013,30(5):172-180.
Qi Hu,Li Yungui,Lv Xilin. A practical elastic plastic damage constitutive model based on energy[J]. Enginee- ring Mechanics,2013,30(5):172-180.(in Chinese)
[5] 胡 峰. 基于断裂力学和损伤理论的裂隙岩体损伤机理研究[D]. 重庆:重庆大学,2015.
Hu Feng. Based on the theory of fracture mechanics and damage mechanism of fractured rock mass damage is studied[D]. Chongqing:Chongqing University,2015.(in Chinese)
[6] 石峻峰,余天庆,戴 杰. 基于能量理论混凝土材料Ⅰ型裂纹损伤与断裂耦合研究[J]. 水利学报,2012(s1):161-167.
Shi Junfeng,Yu Tianqing,Dai Jie. Research on crack da- mage of concrete materials styleⅠand fracture coupling based on energy theory[J]. Journal of Water Conservancy,2012(s1):161-167.(in Chinese)
[7] 蔡四维,蔡 敏.纤维混凝土的损伤理论[J]. 合肥工业大学学报自然科学版,2000,23(1):73-77.
Cai Siwei,Cai Min. On the application of continuum damage theory to fiber reinforced concrete[J]. Journal of HEFEI University of Technology,2000,23(1):73-77.(in Chinese)
[8] 李淑春,刁 波,叶英华,等. 基于能量方法的分段曲线混凝土损伤模型[J]. 工业建筑,2007,37(5):1-4.
Li Shuchun,Diao Bo,Ye Yinghua,et al. Segment curve damage constitutive model of concrete based on energy method[J]. Industrial Architecture,2007,37(5):1-4.(in Chinese)
[9] 胡 琨. 基于损伤和能量原理的单层网壳抗震性能研究[D]. 北京:北京工业大学,2014.
Hu Kun. Research on earthquake resistant behavior of sing-layer latticed shell based on damage and energy theory[D]. Beijing:Beijing University of Technology,2014.(in Chinese)
[10] 陈晓强. 基于能量指标的结构损伤识别理论与试验研究[D]. 武汉:华中科技大学,2009.
Chen Xiaoqiang. Research on structure damage identify theory and experiment based on energy index[D]. Wuhan:Huazhong University of Science and Technology,2009.(in Chinese)
[11] 周家伍,刘元雪,李忠友. 基于能量方法的结构性土体损伤演化规律研究[J]. 岩土工程学报,2013,35(9):1689-1695.
Zhou Jiawu,Liu Yuanxue,Li Zhongyou. Damage evolu-ton of structured soil based on energy method[J]. Chinese Journal of Geotechnical Engineering,2013,35(9):1689-1695.(in Chinese)
[12] 赵亚楠. 基于损伤理论的黄土及黄土边坡渐进破坏研究[D]. 咸阳:西北农林科技大学,2015.
Zhao Yanan. Research on loess and loess slope progressive failure based on damage theory[D]. Xian Yang:Northwest Agriculture Forestry University,2015.(in Chinese)
[13] 郑山锁,秦 卿,任梦宁,等. 基于Najar能量法的混凝土分形损伤本构模型研究[J]. 功能材料,2015,21(46):21001-21006.
Zheng Shansuo,Qin Qing,Ren Mengning,et al. Research on damage constitutive model of concrete based on Najar energy method[J]. Functional Materials,2015,21(46):21001-21006.(in Chinese)
[14] 安丽媛,朱为玄,卓鹏飞,等.损伤与断裂耦合效应的能量理论研究与应用[J]. 河海大学学报自然科学版,2012,40(2):201-205.
An Liyuan,Zhu Weixuan,Zhuo Pengfei,et al. Energy theory and its application to damage and fracture coupling effect[J]. Journal of Hohai University Natural Sciences,2012,40(2):201-205.(in Chinese)
[15] 石峻峰,余天庆,戴 杰. 基于能量理论混凝土材料Ⅰ型裂纹损伤与断裂耦合研究[J]. 水利学报,2012,43:161-167.
Shi Junfeng,Yu Tianqing,Dai Jie. Research on crack damage and fracture coupling of concrete materials typeⅠbased on energy theory[J]. Journal of Water Conservancy,2012,43:161-167.(in Chinese)
[16] 赵 冰,杨荣锋,刘 智,等. 初始损伤对混凝土强度尺寸效应的影响[J]. 交通科学与工程,2016,32(1):60-66.
Zhao Bing,Yang Rongfeng,Liu Zhi,et al. Influence of initial damage on the size effect of concrete strength[J]. Journal of Transport Science and Engineering,2016,32(1):60-66.(in Chinese)
[17] 张 泷,刘耀儒,杨 强,等. 考虑损伤的内变量黏弹-黏塑性本构方程[J]. 力学学报,2014,46(4):572-581.
Zhang Long, Liu Yaoru, Yang Qiang, et al. Viscoelastic-viscoplastic constitutive equation of internal variable considering damage[J]. Chinese Journal of Theoretical and Applied Mechanics,2014,46(4):572-581.(in Chinese)
[18] 侯佳琳. 介质破坏的梯度损伤理论及其数值模拟研究[D]. 长沙:长沙理工大学,2012.
Hou Jialin. Study on gradient theory of dielectric breakdown and numerical simulation[D]. Changsha:Changsha University of Science and Technology,2012.(in Chinese)
[19] 杨云浩,陈鸿杰,王 伟. 弹塑性各向异性损伤模型的 FLAC3D开发与数值验证[J]. 长江科学院院报,2013,30(12):48-59.
Yang Yunhao,Chen Hongjie,Wang Wei. FLAC3D development and numerical verification of elastic-plastic anisotropic damage model[J]. Journal of Yangtze River Scientific Research Institute,2013,30(12):48-59.(in Chinese)
[20] 刘 军,林 皋. 适用于混凝土结构非线性分析的损伤本构模型研究[J]. 土木工程学报,2012,45(6): 50-57.
Liu Jun,Lin Gao. Study of damage constitutive model applied to simulate nonlinear behavior of concrete structures[J]. China Civil Engineering Journal,2012,45(6):50-57.(in Chinese)
[21] Krajcinovic D,Lemartre J. Continuum damage mech-anics theory and applications[M]. New York, USA: Springer-Verilag,1987.
[22] GB 50010—2010混凝土结构设计规范[S].
GB 50010—2010 concrete structure design code[S].(in Chinese)
[23] 徐 娜. 钢筋混凝土构件损伤的识别与判定[D]. 哈尔滨:哈尔滨工业大学,2008.
Xu Na. Damage determine and identification of reinforced concrete structure[D]. Harbin:Harbin Institute of Technology,2008.(in Chinese)
[24] 蔡思维,蔡 敏. 混凝土的损伤断裂[M]. 北京:人民交通出版社,1999.
Cai Siwei,Cai Min. The damage of concrete fracture[M]. Beijing:China Communications Press,1999.(in Chinese)
【中文责编:坪梓;英文责编:之聿】
2017-03-02;Accepted2017-06-16
Lecture Xu Na.E-mail:174600556@qq.com
Thecompressiondamageconstitutivemodelofconcretebasedonthetheoryofenergyloss
XuNa1andFuXueyi2
1) College of Architectural Engineering, Guangdong Polytechnic of Science and Technology, Zhuhai 519090, Guangdong Province, P.R.China2) College of Civil Engineering, Shenzhen University, Shenzhen 518060, Guangdong Province, P.R.China
Based on Najar damage theory, according to ‘Code for design of concrete structure’ (GB50010—2010), we put forward a new generic formula of concrete compression damage constitutive model, and propose the damage evolution equation, which describes complete and non-simplified damage condition in the process of uniaxial compression of concrete preferably. For common strength grade concrete, the compression damage constitutive curve and damage variable equations are given. The concrete damage curves of different strength grades are analyzed contrastively. By using finite element software ABAQUS, we simulate the cylinder shear wall of rectangular section reinforced concrete, and draw the skeleton curve of ultimate bearing capacity under theory condition. Through fitting analysis, we establish the macro relation between materials damage and structure destruction, which verifies that the assumption is reasonable. The advantages of this constitutive model are that the parameters are less and its mathematical form is simple and practical, and that the precision is higher, which provides another solution with compression damage simulation analysis of concrete structure.
concrete; energy loss; Najar damage theory; compression injury; constitutive model; damage evolution equation
Foundation:National Natural Science Foundation of China (50778113,90715012)
:Xu Na,Fu Xueyi.The compression damage constitutive model of concrete based on the theory of energy loss[J]. Journal of Shenzhen University Science and Engineering, 2017, 34(6): 604-610.(in Chinese)
TU 375
A
10.3724/SP.J.1249.2017.06604
国家自然科学基金资助项目(50778113,90715012)
徐 娜(1983—),女,广东科学技术职业学院讲师、博士.研究方向:钢管混凝土结构. E-mail:174600556@qq.com

