大型成品油管道调度的开泵方案优化
梁永图, 周星远, 颜筱函, 张浩然, 刘 静
(1.中国石油大学城市油气输配技术北京重点实验室,北京 102249; 2.中国石化销售有限公司华南分公司,广东广州 510500)
大型成品油管道调度的开泵方案优化
梁永图1, 周星远1, 颜筱函1, 张浩然1, 刘 静2
(1.中国石油大学城市油气输配技术北京重点实验室,北京 102249; 2.中国石化销售有限公司华南分公司,广东广州 510500)
在输送计划一定的情况下合理制定成品油管道沿线各个泵站的开泵方案,可以确保成品油管道安全、经济地运行。在对成品油管道顺序输送问题深入分析的基础上,以沿线泵站动力费用总和最少为目标函数,建立成品油管道调度的优化开泵方案数学模型,模型采用离散时间表达。采用蚁群算法与动态规划算法混合求解模型,以西南成品油管道为例进行模拟计算,并将两种算法混合求解的计算结果与采用动态规划算法和遗传算法单独求解结果进行对比。结果表明:输油计划中的关键时刻采用动态规划算法求解,非关键时刻采用蚁群算法求解。相比于前人所采用的算法,在保证所求开泵方案经济性的基础上,大幅度提高了求解计算效率,从而确保大型成品油管道稳定、高效地运行,符合现场工艺要求。
成品油管道; 开泵方案优化; 混合求解; 蚁群算法; 动态规划算法; 遗传算法
梁永图等[1-2]采用动态规划算法对成品油管道、成品油管网开泵方案进行了优化求解;陈媛媛等[3]以西南成品油管道泵站为例,运用动态规划算法解决了配有调速泵的成品油管道全线开泵方案优化问题;刘承婷等[4]采用(0-1)规划算法建立最优开泵方案;崔艳雨等[5]提出了具有原理简单、计算速度快、易于程序化等优点的两阶段优化法;崔艳雨等[6]、杨雪等[7]采用遗传算法分别以西南成品油管道、西部成品油管道为例优化配泵方案。国外除了利用动态规划算法进行开泵方案优化之外,还有使用其他数学规划方法和人工智能算法的相关研究。Ferreira等[8-9]采用动态规划方法、Ehsan Abbasi等[10-11]使用线性规划法、Costa等[12]使用分支定界法求解最优开泵方案;Barreto等[13]基于所有型号配泵的能耗数据考虑到操作便捷性,建立以能耗最低为目标函数的开泵方案数学模型;Ribas等[14]利用微观遗传算法求解泵站调度数学模型;Al-Ani等[15]利用多目标粒子群优化算法求解出相对经济的泵调度方案。大型成品油管道管线长、泵站多、调度周期长,若采用动态规划或者(0-1)规划等数学规划算法[16],虽然准确性、经济性相对较高,但随着模型规模增大,计算时间会成倍增长。若采用遗传算法、粒子群算法等智能算法求解[17-19],虽然可以避免计算效率过低的问题,但是由于算法本身的局限性,求解结果的最优性和经济性不高。基于动态规划算法与蚁群算法的特点[20-22],笔者提出将两种算法相结合的方式基于离散时间表达对大型成品油管道输送过程开泵方案进行优化,运用动态规划算法求解输油计划中关键时刻的开泵方案并作为之后蚁群算法的初始解,再利用蚁群算法全局搜索能力强、收敛性强的特点[23]求解非输油关键时刻的开泵方案。
1 模型假设
成品油管道系统水力工况十分复杂,各变量间非线性耦合关系较强[24]。在构建数学模型时,为保证模型的有效性和准确性,须将复杂的管道系统合理简化,以便于数学模型的建立和求解[25-26]。针对成品油管道的特征,假设如下:
(1)管道中的油品是不可压缩流体;
(2)管道运行状态看作稳态过程;
(3)不考虑混油段的影响;
(4)按等温管道进行计算,不考虑沿线温度变化对油品的密度和黏度的影响。
2 模型建立
针对成品油管道大口径、变流量、多批次、沿线多点进出的特点[27],应用最优化理论,建立管道稳态输送的数学模型。根据成品油管道不同输送条件和水力特性的变化,在满足泵站进出站压力约束、管道设计压力约束、特殊点位置处压力约束以及能在相应时间内完成批次计划[28]等条件下,建立成品油管道调度的优化开泵方案数学模型,确定出全线各个泵站最优开泵方案,达到全线总能耗最小的目标,降低成品油管道输送过程中的运行费用[29]。
2.1 目标函数
对设有I个泵站且第i个泵站配置Ki台离心泵的成品油管道系统(所有站场视为泵站,非泵站其Ki=0),当转速固定且不考虑用电费用波动时,其目标函数为
(1)
式中,Y为成品油管道全线泵站总能耗成本,元;TD为输送周期,h;Fe为电价,元/(kW·h);ηij为第i个泵站第j台泵的效率;Cij为第i个泵站第j台泵的运行状态,若处于开启状态,Cij=1;若不处于开启状态,Cij=0;ρi为第i个泵站输送油品密度,kg/m3;Qij为第i个泵站第j台泵的过泵流量,m3/s;aij,bij为第i个泵站第j台泵的泵特性常数。
2.2 约束条件
2.2.1 压力约束
pi=ρigHi,
(2)
(3)
pINi≥pImini,
(4)
pINi≤pImaxi,
(5)
pouti≥pomini,
(6)
pouti≤pomaxi.
(7)
式中,pi为第i个泵站提供的压力,Pa;Hi为第i个泵站提供的扬程,m;ps为管道首站出站压力,Pa;pd为管道末站进站压力,Pa;pf为管道沿程摩阻损失,Pa;pz为高程压力损失,Pa;pm为站内压力损失,Pa;pINi为第i个泵站的油品进站压力,Pa;pImini和pImaxi分别为第i个泵站允许最低和最高进站压力,Pa;pouti为第i个泵站出站压力,Pa;pomini和pomaxi分别为第i个泵站允许最低和最高出站压力,Pa。
约束条件中的式(3)为能量平衡约束条件,保证在任意时刻管道内部的能量守恒;式(4)、(5)为泵站进站压力约束条件,油品输送到某一泵站时,进站压力必须大于泵站的最小进站压力且小于泵站的最大进站压力;式(6)、(7)为泵站出口压力约束;以确保下游管线和站场处在允许操作压力范围[30-31]。
2.2.2 流量约束
约束条件为
Qmini≤Qgi≤Qmaxi,
(8)

(9)
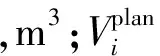
2.2.3 泵站特性约束
对于转速不变的泵机组,可通过泵设计规范手册上的扬程和流量数据,采用最小二乘法拟合出泵的特性方程为
(10)
式中,hij为第i个泵站第j台泵提供的扬程,m。
若泵站由多台泵串联组合而成,通过每台泵的排量相等,可计算出泵站的泵组合数和泵机组所提供的扬程,对于任意一个泵站有
(11)
2.2.4 开泵数目约束
管道沿线泵站须满足方案约束:
ni≤NPi.
(12)
式中,ni为第i个泵站开泵方案数目;NPi为第i个泵站不同型号泵可排列组合的泵机组数目。
2.2.5 泵运行时间约束
为了增加输油泵运行的稳定性,每台泵开启一次之后的连续运行时长必须大于所要求的运行时长下限:
TP,ij≥Tpmini,j.
(13)
式中,TP,ij为第i个泵站第j台泵的实际运行时长,h;Tpmini,j为第i个泵站第j台泵的最低运行时长,h。
3 模型求解
采用动态规划算法与蚁群算法两种算法结合的方式在已知输油计划的基础上求解大型成品油管道最优开泵方案。动态规划算法适用领域广、结果准确,特别是对于采用离散变量的数学模型,求解成品油管道最优开泵方案比较有效、实用。但当管线过长、泵站较多以及选取时步较短时会出现模型规模较大的情形,动态规划算法易导致维数灾难、求解效率低[33-34]。若初始解设置合适,蚁群算法收敛性较强、有较强的全局搜索能力,是一种正反馈和自组织的算法[35]。针对两种算法的以上特点,在泵站数目较多、调度周期较长的大型成品油管道开泵方案优化问题研究中,工况变化较大的关键时间点采用动态规划算法求解,工况变化不大的时间点依靠前一时刻开泵方案作为初始解采用蚁群算法求解,可以在泵站较多的条件下提高搜索速度并确定较优的此时刻开泵方案。由此可见,采用两种算法混合求解可以提高大型成品油管道开泵方案的求解效率,并且保证方案的经济性。
3.1 动态规划算法求解
输油计划关键时间点的最优开泵方案采用动态规划算法确定,因为输油计划关键时间点的工况变化大,一般由注入、分输操作开始或结束、流量变化、切换油品等操作引起。此类时刻的开泵方案与上一时刻相比变化较大,采用动态规划算法求解更加准确,且因为整个调度周期内此类时刻数量较少,并不会出现维数灾难的问题。
3.1.1 变量描述
(1)阶段变量。油品从首站入口到第i个泵站出口为第i阶段,将全线的泵站分割成若干个相互联系的阶段。
(2)状态变量。状态变量表示每个阶段管道的运行状况,将油品到达第i个泵站出口时前面所需要的泵提供压力总和(包括第i个泵站)作为第i阶段的状态变量Si。Si满足状态变量的无后效性,即某一阶段的开泵方案只能通过当前的状态确定未来的开泵方案,当前的状态是以往开泵方案的一个总结。
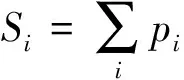
(14)
(3)决策变量。由于不考虑管道运行时的电费波动,所以管道某一阶段前所有泵站所消耗的总功率就决定了管道的能耗成本,且泵的功率与其提供的压力直接相关,每个阶段的状态受到泵提供压力的控制,即把管道各泵机组提供的实际压力pi为决策变量。
3.1.2 方程建立
(1)状态转移方程:
Si=Si-1+pi.
(15)
(2)递推方程:
Yi(Si)=min{Yi-1(Si-1)+Yi(pi)}.
(16)
式中,Yi为第i个泵站之前(包括第i个泵站)能耗之和。
3.1.3 求解步骤
(1)根据管道初始状态,通过计算体积坐标确定各个时刻批次界面的具体位置。根据管道的基本运行参数,判断其流态,从而算出相应的水力坡降。将相关数据代入计算公式得出管道在各个阶段运行时的水力工况。
(2)按照油品流动方向,对首站入口至各泵站出口的过程划分阶段,从首站入口至第i站出口为第i阶段,获取每一个阶段的决策变量pi,从而计算得出每一阶段的状态变量Si。
(3)由每一阶段的状态变量Si得到该阶段能耗Yi(Si),应用动态规划的方法,最后计算到第I阶段,得到最优运行成本minY,以第I阶段的最省费用为起点,逆推确定出每个泵站的最优开泵方案。
3.2 蚁群算法求解
非输油计划关键时间点的最优开泵方案利用蚁群算法求解,由于此类时刻数量众多并且相邻时刻开泵方案变化一般相对较小,若采用动态规划算法求解,求解时间会成倍增长。采用蚁群算法求解,以上一时刻开泵方案作为此时刻求解的初始解,初始解与最优解的距离相对较小,基于蚁群算法以上特点,能够较快收敛找到最优解,计算效率高并且结果准确。
3.2.1 目标函数
将蚁群算法应用于成品油管道开泵方案优化当中,目标函数的选取至关重要,直接决定了找到最优解的速度以及蚂蚁各个时刻所处位置的优劣程度等。本文中的成品油管道开泵方案优化研究以能耗最低为目标函数,为满足蚁群算法目标函数最大化的特点,须将模型的目标函数转化为极大值函数:
F=c-Y+(B-1)M.
(17)
式中,Y为全线各泵站开泵方案的能耗费用之和;M为极大值;B为末站进站压力二元变量,若末站进站压力大于零,即全线各泵站提供的能量大于沿程摩阻损失,则B=1;若末站进站压力小于零,即全线各泵站提供的能量小于沿程摩阻损失,B=0;c为常数,具体求解可设定不同值以确保B=1时,目标函数F为正值。
3.2.2 问题转化
将成品油管道上的I个泵站设为N维空间,每个泵站内输油泵所能组合的开泵方案总数NPi为第n维的长度,N维空间内每一个位置即表示成品油管道的每种开泵方案,将每一个位置的数据代入目标函数,求得结果作为蚁群算法的食物浓度值对每个位置进行判断。将成品油管道开泵方案优化问题转化为利用蚁群算法寻找最优位置。
3.2.3 求解步骤
(1)确定蚂蚁数量m、移动次数T、食物浓度挥发常数Rou以及搜索上下限等基础参数,并设置蚂蚁的初始位置,即上一时刻开泵方案在N维空间中对应的位置,求出此位置的食物浓度值。
(2)蚂蚁根据状态转移概率方程选择要转移的位置,已经走过的位置禁止再次访问,以避免已经探索过的开泵方案再次探索。
(18)
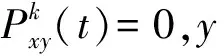
(19)
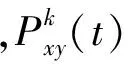
(3)所有蚂蚁完成一次移动之后,更新各位置的食物浓度值,包含食物浓度的挥发以及走过的蚂蚁食物浓度的释放。
(20)

(4)所有移动完成后,食物浓度值最高的位置为最优解,即该时刻的最优开泵方案。
本文中提出的成品油管道开泵方案优化过程较好地利用了两种算法的优点,避免了缺点,提高了大型成品油管道开泵方案优化的效率,减少了计算时间。
用具体的算法程序框图表示算法结构,见图1。
4 计算实例
以西南成品油管道主干线为例,管线全长1 874.27 km,有18个站场包含2个注入站、14个分输站、15个泵站,调度周期持续一个月,属于大型成品油顺序输送管道,具有管道长、站场多、调度周期长的特点。对于西南成品油管道晴隆泵站调速泵,计算中采用转速离散化的方法,将其视为一系列不同转速的固定转速泵[3]。
利用本文中提出的优化方式,基于批次运行计划对成品油管道开泵方案进行优化,运行计划批次运移图如图2所示。

图2 输油计划批次运移图Fig.2 Batch migration diagram of oil transportation plan
图中,左侧纵坐标轴代表管道的初始状态,蓝色表示92#汽油、红色表示0#车柴、黄色表示0#普柴,管道初始时刻存在两段0#车柴、两段0#普柴、一段92#汽油,右侧纵坐标轴表示管道沿线站场的里程。图中,横向矩形段表示注入(分输)站的注入(分输)操作,起、终点对应到横轴时间轴分别代表操作的开始、结束时刻,矩形段宽度代表注入(分输)流量大小,每种颜色代表注入(分输)该颜色对应的油品。图中黑线表示各个混油界面在管道中的运移过程,斜率代表混油界面运移的速度。
使用Intel Xeon E5-2630 v3(2.4 GHz)处理器电脑、运用MATLAB R2015a软件编程进行求解,求解过程中蚁群算法参数配置如下:蚂蚁数量m=300;蚂蚁移动次数T=80;食物浓度挥发系数Rou=0.9。整个调度过程持续744 h,时间间隔普遍为2~3 h,最小时间间隔为55 min,共为全线所有泵站各配泵312次,得到部分优化开泵方案结果如表1所示,部分站场进、出站压力曲线如图3所示。

表1 部分优化开泵方案Table 1 Optimal pump start-up scheme 台
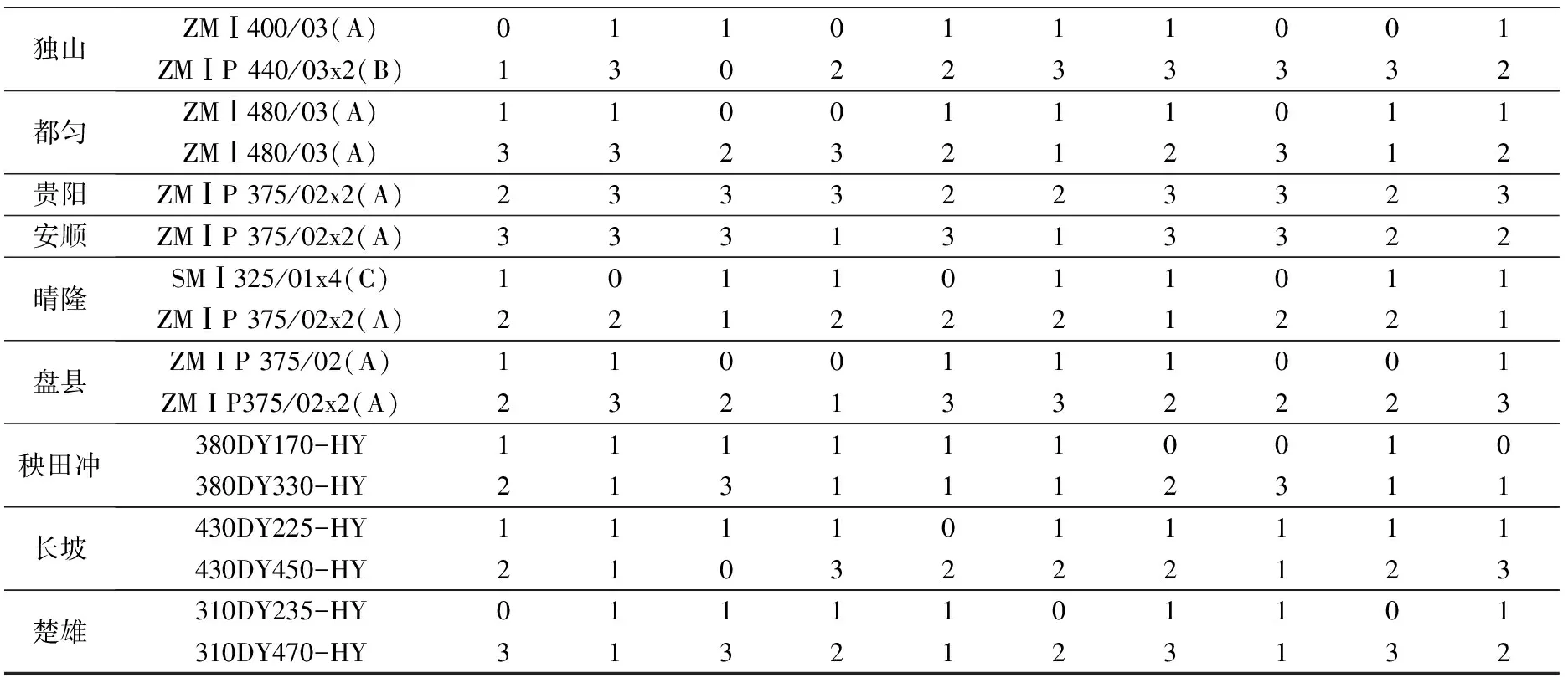
续表1

图3 部分站场进出站压力曲线Fig.3 Inlet and outlet pressure changes of part stations
求解结果中各站进出站压力均能满足模型中设定的该站的进出站压力约束,由于文章篇幅限制,本文中选取茂名首站和贵阳分输泵站为例进行说明。其中图3(a)为茂名首站出站压力曲线、图3(b)为贵阳分输泵站进站压力曲线、图3(c)为贵阳分输泵站出站压力曲线。从图3可以看出,茂名首站和贵阳分输泵站在管道运行过程中的进出站压力在要求压力范围之内,能够避免发生超压或者欠压事故,确保管道运行的安全性。由于所运行的输油计划340~380 h时段全线除黎塘——柳州段其他管段停输,根据“保压停输”原则,茂名首站和贵阳分输泵站在该时段内的压力近似等于前一时段压力。
针对西南成品油管道晴隆泵站调速泵,优化求解过程中将其离散为一系列不同转速的定转速泵处理,部分时刻求得转速如下:0 h时调速泵转速为2 980 r/min;145 h时调速泵转速为2 793 r/min;525 h时调速泵转速为2 607 r/min;716 h时调速泵转速为2 235 r/min。
将本文中采取的混合优化求解的方式与采用文献[3]中的动态规划算法和文献[7]中的遗传算法单独求解的求解结果进行对比,3种优化方式求得各站节流压力损失之和如图4所示。
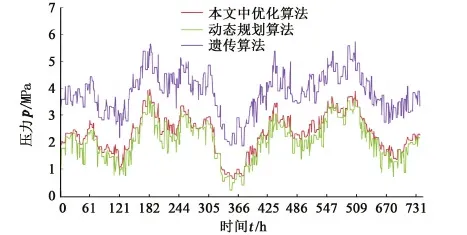
图4 各站节流压力损失之和Fig.4 Sum of pressure loss by throttling of each station
采用文献[3]中单一动态规划算法求解,计算耗时为132.26 h,管道运行总耗电量为1.261×107kW·h;采用文献[7]中的遗传算法求解,求解时间为2.78 h,管道运行总耗电量为1.923×107kW·h,求解结果最优性相对较低。采用本文的优化方式求解,求解时间为4.15 h,管道运行总耗电量为1.269×107kW·h,相比于动态规划算法,计算效率提高约31倍,运行能耗总体升高约0.6%;相比于遗传算法,计算时间延长近0.5倍,运行能耗总体降低近34%,输送经济性良好。
从采用不同算法求解大型成品油管道调度开泵方案的计算结果来看,应用动态规划算法的求解结果相比于本文中所提出的优化方式虽然管道运行总耗电量有小幅度下降,但是求解时间过长,问题规模过大导致的维数灾难问题已略有体现。并且由于成品油管道输送的调度问题与水力特性比较复杂,管道实际运行过程中可能会受到特殊状况与人为因素的影响等原因,输油现场在管道运行过程中可能须根据输油计划实际执行情况对原有输油计划多次修改并进行水力校核与开泵方案的优化制定。采用动态规划算法求解大型成品油管道开泵方案的求解效率已经不能满足现场要求,甚至可能影响管道的实际运行。而本文中所提出的采用动态规划算法与蚁群算法混合求解的优化方式,虽然相比于动态规划算法单独求解能耗有微小提升,但是具有较高的求解效率,可以保证管道连续、稳定地运行。因此综合来看,采用动态规划算法和蚁群算法混合优化大型成品油管道调度的开泵方案问题能够同时具有较高的求解效率和较好的求解效果,符合现场工艺要求。
5 结束语
考虑成品油管道运行过程中的压力约束、流量约束和泵站特性约束等约束条件,建立了以各泵站动力费用之和最小为目标函数的成品油管道运行优化数学模型。针对大型成品油管道开泵方案优化问题采用动态规划算法和蚁群算法混合求解,输油计划中的关键时刻采用动态规划算法求解,非关键时刻采用蚁群算法求解。在保证良好求解效果的前提下大幅度提高了求解效率。
[1] 梁永图,宫敬,康正凌,等.成品油管道优化运行研究[J].中国石油大学学报(自然科学版),2004,28(4):97-101.
LIANG Yongtu, GONG Jing, KANG Zhengling, et al. Optimal operation of multi-product pipeline [J].Journal of the University of Petroleum, China(Edition of Natural Science),2004,28(4):97-101.
[2] 梁永图,刘增哲.成品油管网运行优化[J]. 中国石油大学学报(自然科学版),2011,35(3):115-118.
LIANG Yongtu, LIU Zengzhe. Optimal operation of multi-product pipeline network[J].Journal of China University of Petroleum(Edition of Natural Science), 2011,35(3):115-118.
[3] 陈媛媛,吴先策,纪荣亮.动态规划法在西南管道泵站优化运行中的应用[J].油气储运,2009,28(8):13-15.
CHEN Yuanyuan, WU Xiance, JI Rongliang. Application of dynamic programming theory in optimized operation of pump station over west south oil product pipeline [J].Oil & Gas Storage and Transportation,2009,28(8):13-15.
[4] 刘承婷,邵振军,刁望庆.轻质油输送优化模型与开泵方案[J].东北石油大学学报,2006,30(1):43-46.
LIU Chenting, SHAO Zhenjun, DIAO Wangqing. Optimal modeling of the light oil transportation and pumping[J]. Journal of Northeast Petroleum University, 2006,30(1):43-46.
[5] 崔艳雨,陈世一,梁静华,等.确定开泵方案的两阶段优化法[J].石油化工高等学校学报,2005,18(4):66-68.
CUI Yanyu, CHEN Shiyi, LIANG Jinghua, et al. Two stages optimizing method on determining the process parameters[J]. Journal of Petrochemical Universities, 2005,18(4):66-68.
[6] 崔艳雨,吴明,张国忠.基于IPGA的成品油管道优化研究[J].石油化工高等学校学报,2007,20(4):63-67.
CUI Yanyu, WU Ming, ZHANG Guozhong. The product pipeline optimization based on IPGA[J]. Journal of Petrochemical Universities, 2007,20(4):63-67.
[7] 杨雪,吴先策,纪荣亮.西南成品油管道泵站优化运行[J].油气储运,2011,30(3):196-199.
YANG Xue, WU Xiance, JI Rongliang. The optimized operation of pump stations in southwest products pipeline[J].Oil & Gas Storage and Transportation,2011,30(3):196-199.
[8] JOSÉ A S F, RENÉ V V V. Optimization of a pump-pipe system by dynamic programming[J]. Engineering Optimization, 1984,7(3):241-251.
[9] LI K, ZUO K, WANG J, et al. Dynamic programming example analysis of a pump station[J]. Physics Procedia, 2012,24:1796-1800.
[10] ABBASI E, GAROUSI V. An MILP-based formulation for minimizing pumping energy costs of oil pipelines: beneficial to both the environment and pipeline companies[J]. Energy Systems, 2010,1(4):393-416.
[11] PULEO V, MORLEY M, FRENI G, et al. Multi-stage linear programming optimization for pump scheduling[J]. Procedia Engineering, 2014,70:1378-1385.
[12] COSTA L H M, PRATA B D A, RAMOS H M, et al. A Branch-and-bound algorithm for optimal pump scheduling in water distribution networks[J]. Water Resources Management, 2015,30(3):1-16.
[13] BARRETO C V, PIRES L F G, AZEVEDO L F A. Optimization of pump energy consumption in oil pipelines[C]. Calgary: International Pipeline Conference(IPC), 2004.
[14] RIBAS P C, YAMAMOTO L, POLLI H L, et al. A micro-genetic algorithm for multi-objective scheduling of a real world pipeline network[J]. Engineering Applications of Artificial Intelligence, 2013,26(1):302-313.
[15] AL-ANI D, HABIBI S. Optimal pump operation for water distribution systems using a new multi-agent particle swarm optimization technique with EPANET[C]. Montreal: Electrical & Computer Engineering (CCECE), 2012.
[16] 张浩然,梁永图,王宁,等. 多源单汇多批次顺序输送管道调度优化[J]. 石油学报,2015,36(9):1148-1155.
ZHANG Haoran, LIANG Yongtu, WANG Ning, et al. Optimal scheduling of multi-source single-distribution pipeline with multi-batch sequential transportation[J].Acta Petrolei Sinica,2015,36(9):1148-1155.
[17] 黄小侨,李娜,李军,等.基于遗传算法的常减压装置多目标优化[J]. 中国石油大学学报(自然科学版),2016,40(2):163-168.
HUANG Xiaoqiao, LI Na, LI Jun, et al. Multi-objective optimization of crude and vacuum distillation system based on genetic algorithm [J].Journal of China University of Petroleum (Edition of Natural Science), 2016,40(2):163-168.
[18] 梁永图,张浩然,邵奇.成品油管网调度优化研究进展[J].油气储运,2015,34(7):685-688.
LIANG Yongtu, ZHANG Haoran, SHAO Qi. Progress in the study on scheduling optimization of products pipeline network [J].Oil & Gas Storage and Transportation, 2015,34(7):685-688.
[19] 张凯,吴海洋,徐耀东,等.考虑地质及开发因素约束的三角形井网优化[J]. 中国石油大学学报(自然科学版),2015,39(4):111-118.
ZHANG Kai, WU Haiyang, XU Yaodong, et al. Triangulated well pattern optimization constrained by geological and production factors [J].Journal of China University of Petroleum (Edition of Natural Science), 2015,39(4):111-118.
[20] 王逢德,肖文生,刘健,等. 基于改进粒子群算法的海洋钻机系统布局优化[J]. 中国石油大学学报(自然科学版),2016,40(2):123-128.
WANG Fengde, XIAO Wensheng, LIU Jian, et al.Research on layout optimization of drilling rig system of semi-submersible platform based on modified particle swarm optimization [J].Journal of China University of Petroleum (Edition of Natural Science),2016,40(2):123-128.
[21] ZHANG H R, LIANG Y T, XIAO Q, et al. Supply-based optimal scheduling of oil product pipelines [J]. Petroleum Science, 2016,13(2):355-367.
[22] CAFARO V G, CAFARO D C, CERDA J. Improving the mathematical formulation for the detailed scheduling of refined products pipelines by accounting for flow rate dependent pumping costs[J]. Iberoamerican Journal of Industrial Engineering, 2014,5(10):115-128.
[23] 刘刚,许继凯,国志刚,等. 星状集输管网拓扑结构的整体优化[J]. 中国石油大学学报(自然科学版),2016, 40(4):133-140.
LIU Gang, XU Jikai, GUO Zhigang, et al. Global optimization of topological structure for radial pattern gathering pipe network[J].Journal of China University of Petroleum (Edition of Natural Science),2016,40(4):133-140.
[24] CAFARO V G, CAFARO D C, MENDEZ C A, et al. MINLP model for the detailed scheduling of refined products pipelines with flow rate dependent pumping costs[J]. Computers & Chemical Engineering, 2015,72:210-221.
[25] 马立新,申龙涉,孟祥谦,等.长输管道泵机组优化数学模型[J].油气储运,2010,29(4):272-273.
MA Lixin, SHEN Longshe, MENG Xiangqian, et al. Mathematical model for pump unit optimization of long distance pipelines[J].Oil & Gas Storage and Transportation, 2010,29(4):272-273.
[26] LIANG Y T, LIM, ZHANGN. A study on optimizing delivering scheduling for a multiproduct pipeline[J]. Computers & Chemical Engineering, 2012,44:127-140.
[27] 康正凌,宫敬,梁永图.成品油管道运行电费优化研究[J].天然气与石油,2011,29(2):1-3.
KANG Zhengling, GONG Jing, LIANG Yongtu. Study on operation electric charge optimization of product oil pipeline [J]. Natural Gas and Oil,2011,29(2):1-3.
[28] 朱培明,陈志华,邹斌,等.克乌成品油管道复线泵机组的优化运行方案[J].油气储运,2012,31(3):221-224.
ZHU Peiming, CHEN Zhihua, ZOU Bin, et al. Optimized running scheme for pump units of second Kalamay-Urumchi products pipeline[J].Oil & Gas Storage and Transportation, 2012,31(3):221-224.
[29] 梁永图.西南成品油管道输送模拟软件[J].油气储运,2006,25(6):11-14.
LIANG Yongtu. The development of simulation software for south-west multi-product pipeline operation[J]. Oil & Gas Storage and Transportation, 2006,25(6):11-14.
[30] 才建,宫敬,李小平. 输油管道过渡过程最优控制策略[J]. 中国石油大学学报(自然科学版),2008,32(2):102-107.
CAI Jian, GONG Jing, LI Xiaoping.Optimal control strategy of transient process on oil pipeline[J].Journal of China University of Petroleum (Edition of Natural Science), 2008,32(2):102-107.
[31] 康正凌,宫敬,严大凡.成品油管道输送高差混油模型研究[J]. 石油大学学报(自然科学版),2003, 27(6):65-67.
KANG Zhengling, GONG Jing, YAN Dafan.Development of model for contaminated oil product caused by elevation difference in multiproduct pipelines [J].Journal of the University of Petroleum, China(Edition of Natural Science), 2003,27(6):65-67.
[32] CAFARO D C, CERDA J. Optimal scheduling of multiproduct pipeline systems using a non-discrete MILP formulation[J]. Computers & Chemical Engineering, 2004,28(10):2053-2068.
[33] 宫敬,储祥萍.成品油管道优化运行方法研究[J].油气储运,2000,19(10):22-25.
GONG Jing, CHU Xiangping. Study of multi-product pipeline optimum operating method [J].Oil & Gas Storage and Transportation,2000,19(10):22-25.
[34] CAFARO D C, CERDA J. Operational scheduling of refined products pipeline networks with simultaneous batch injections[J]. Computers & Chemical Engineering, 2010,34(10):1687-1704.
[35] 王鸿雁,肖文生,刘健,等.深水钻机集成监控系统可靠性冗余优化[J]. 中国石油大学学报(自然科学版),2015,39(1):128-135.
WANG Hongyan, XIAO Wensheng, LIU Jian, et al. Reliability redundancy optimization allocation of integrated monitoring and control system of deep-sea drilling rig[J].Journal of China University of Petroleum (Edition of Natural Science),2015,39(1):128-135.
(编辑 沈玉英)
Optimizationofpumpstart-upschemesforlarge-scalemultiproductpipelines
LIANG Yongtu1, ZHOU Xingyuan1, YAN Xiaohan1, ZHANG Haoran1, LIU Jing2
(1.BeijingKeyLaboratoryofUrbanOilandGasDistributionTechnology,ChinaUniversityofPetroleum,Beijing102249,China;2.SINOPECSalesCompanyLimitedSouthernChinaBranch,Guangzhou510500,China)
With the prerequisite of a specific transportation plan, a reasonable formulation for the pump start-up scheme of pump stations along a multiproduct pipeline can ensure a safe and economical operation condition with low energy consumption. Based on the further study on the multiproduct pipelines batch transportation, in this paper we consider the power cost of pump stations in the multiproduct pipeline system as the objective function, and a mathematical model aiming to optimize the pump start-up scheme for large-scale multiproduct pipelines is established. The model is based on the discrete-time method. The dynamic programming algorithm and the genetic algorithm are together utilized to solve the optimization issue. The south-west multiproduct pipeline is taken as a real case study, and the calculation results solved by the hybrid two algorithms are compared with those by each of the two algorithms. The results show that the dynamic programming algorithm should be used during the key time, and the ant colony algorithm has better to be used in other cases. In comparison with the previous methods to satisfy the economy of the pump start-up scheme, the computational efficiency of the hybrid method is dramatically enhanced, which can guarantee the stable and efficient operation of large-scale multiproduct pipelines and meet the in-situ process requirements.
multiproduct pipeline; pump start-up scheme optimization; hybrid method; ant colony algorithm; dynamic programming algorithm; genetic algorithm
2016-12-16
国家自然科学基金项目(51474228)
梁永图(1971-),男,教授,博士,研究方向为长输管道与油气田集输相关技术。E-mail:13910970411@163.com。
1673-5005(2017)05-0130-09
10.3969/j.issn.1673-5005.2017.05.016
TE 832
A
梁永图,周星远,颜筱函, 等. 大型成品油管道调度的开泵方案优化[J]. 中国石油大学学报(自然科学版), 2017,41(5):130-138.
LIANG Yongtu,ZHOU Xingyuan, YAN Xiaohan, et al. Optimization of pump start-up schemes for large-scale multiproduct pipelines [J]. Journal of China University of Petroleum (Edition of Natural Science), 2017,41(5):130-138.

