固井界面微环隙产生机制及计算方法

赵效锋, 管志川, 史玉才, 李 涛, 廖华林, 蒋金兴, 孙宝江

(1.中国石油大学石油工程学院,山东青岛 266580; 2.中国石化中原油田分公司石油工程技术研究院,河南濮阳 457001)

固井界面微环隙产生机制及计算方法

赵效锋1,2, 管志川1, 史玉才1, 李 涛1, 廖华林1, 蒋金兴1, 孙宝江1

(1.中国石油大学石油工程学院,山东青岛 266580; 2.中国石化中原油田分公司石油工程技术研究院,河南濮阳 457001)

针对油气井生产过程中固井界面微环隙的产生和发展规律进行仿真试验研究,并对套管-水泥环界面的黏结力进行测量,基于以上研究建立固井界面微环隙的理论计算方法。结果表明:套管内压过大导致水泥环产生塑性变形,套管内压减小时固井界面将受拉,实测固井界面存在数量级为0.1 MPa的黏结力,当界面拉力足以克服界面黏结力时,固井界面将会脱离产生微环隙;套管内压值越大,压力卸载后产生微环隙的机率越大,且微环隙尺寸越大;相同胶结质量下固井一界面比二界面更容易产生微环隙;理论计算结果与仿真试验结果具有较好的一致性。

井筒完整性; 微环隙; 仿真试验; 理论计算; 黏结力

在油气井长期生产过程中,固井界面微环隙是导致井筒密封完整性失效的主要原因之一[1-3]。井筒长期完整性涉及油气井生命周期的各个阶段,其失效的原因应该是不同阶段影响因素作用的累积和组合[4]。20世纪90年代初期,水泥环长期力学特性研究引起了学者们的关注[5-6],并通过室内试验发现了井内压力连续变化条件下,过高的井内压力或温度会造成水泥环破坏从而导致井筒密封完整性失效。尽管这些研究中都伴随着微环隙现象的产生,但限于微环隙的尺度和所处环境,当前技术条件无法实现微环隙尺寸的直接测量,至今未见有采用室内试验方法研究微环隙产生机制的报道。随着数值分析方法的逐步完善,尤其是计算机运算速度的飞速发展,部分学者采用有限元模拟方法实现了对不同阶段井筒密封完整性的分析预测[4,7],尽管为微环隙的研究提供了一种有效手段,但针对微环隙产生机制的研究相对较少。在理论计算方面,少数学者通过建立理论模型定量描述了微环隙的产生,其中姚晓、陈勇[8-9]基于弹性力学建立了微环隙理论计算模型,但有研究结果表明[10],水泥环在弹性变形范围内不会产生微环隙,而早前的试验研究[5-6]也有所证实。刘骁[11]建立的微环隙计算模型考虑了水泥环塑性变形,但由于缺乏对微环隙产生机制的认识,所以其计算方法有待修正。初纬[12]基于弹塑性力学建立了连续变化内压下固井界面微环隙的理论计算模型,但由于文中用于对比验证的Jackson[6]试验结果中未对微环隙进行测量,因此其模型的准确性及精度无法验证,以至于该方法跟试验有偏差。对于固井界面微环隙的产生机制及基于此的理论计算方法仍须进一步研究及改进。笔者采用有限元数值模拟方法,对井内压力连续变化条件下的固井界面力学响应进行模拟分析,研究确定固井界面微环隙的产生机制,并对微环隙产生过程中套管-水泥环界面的黏结力进行试验测量,在此基础上,建立固井界面微环隙的理论计算方法,并用有限元模拟结果对该方法进行验证。

1 产生机制

Goodwin等[5]针对井内压力连续变化条件下环空窜流产生的原因开展了试验研究,根据该试验建立如图1所示的压力和温度变化环空渗透率测试装置。装置中将139.7 mm(5-1/2 in)套管置于193.7 mm(7-5/8 in)套管中,形成高度为1.7 m环形空间以灌注水泥浆,并在外管壁顶底端开孔以测量环空渗透率。

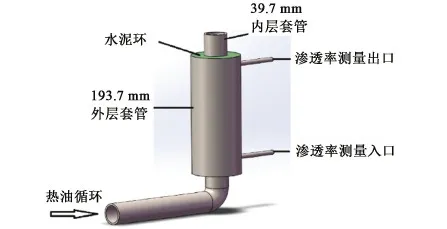
图1 Goodwin试验装置示意图Fig.1 Schematic diagram of Goodwins experimental device

试验过程:①在内外层套管间环空注满不同配方(S1、S2、S3、S4)水泥浆,并在内层套管循环热油(177 ℃)条件下养护,整个养护过程环空内压力保持3.5 MPa;②待水泥凝固以后,在内层套管压力为0 MPa条件下测量水泥环水渗透率;③增加内层套管压力至14 MPa情况下测量水泥环水渗透率;④将内层套管压力降至0 MPa情况下测量水泥环水渗透率;⑤以约14 MPa压力增量重复步骤③和④直到最大内压69 MPa。试验结果如图2、3所示。

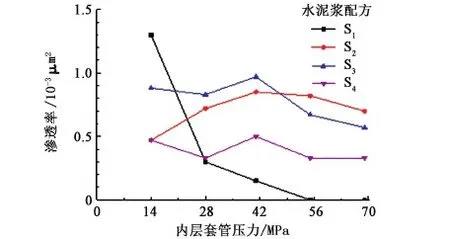
图2 不同套管内压下的环空渗透率Fig.2 Annular permeability with different casing pressure

从图2中可以看出,无论何种水泥配方,套管内持有压力条件下环空渗透率数值较小,且随着内压值的增加,环空渗透率呈下降趋势;从图3中可以看出,套管内卸压为0 MPa条件下,环空渗透率数值远大于套管内持压条件下的测量值,且随着套管内压值的不断增加,套管内压0 MPa条件下的环空渗透率呈上升趋势,初始阶段上升不明显,当内压增至41 MPa后卸压,环空渗透率大幅升高。

采用有限元数值模拟方法对油气井套管内压连续变化条件下的固井界面是否存在微环隙及微环隙的产生原因进行分析。由于是轴对称问题,模拟建立如图4所示的1/4套管-水泥环-地层组合体模型[13]。

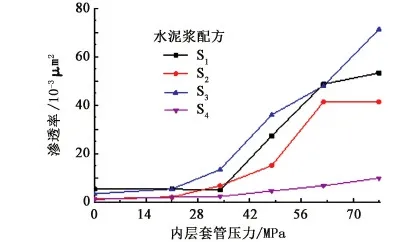
图3 套管内压为0 MPa条件下的环空渗透率Fig.3 Annular permeability with casing pressure 0 MPa

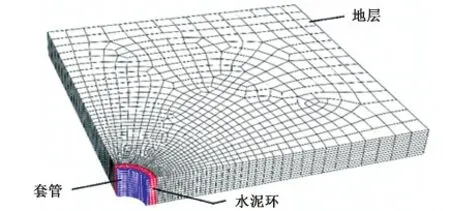
图4 套管-水泥环-地层组合体三维有限元模型Fig.4 3D finite element model of casing-cement sheath-stratum

模型所处位置垂深4 000 m,模型厚度取大于井眼半径的5%以消除端部效应,上覆岩层压力梯度0.013 MPa/m,远场地应力与垂向地应力比为0.67。模型几何参数和材料特性如表1所示。另外,套管-水泥环界面的黏结力通过试验测定,该试验在套管与水泥环完全接触的理想状态下进行,不考虑温度、压力等条件对结果的影响。测量原理与结果如图5所示。

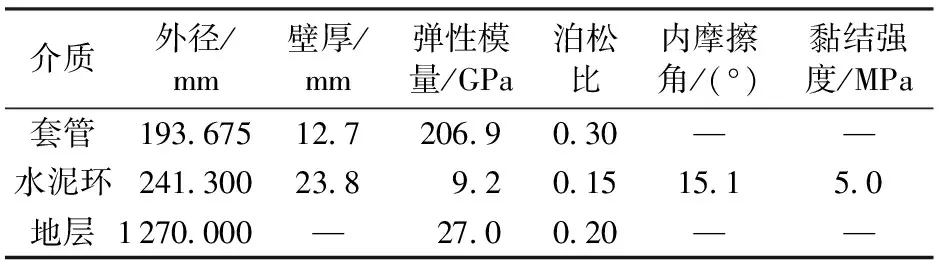
表1 模型几何参数和材料特性Table 1 Geometrical parameter and material properties of model media

从上述测定试验结果可以看出,水泥与钢板之间存在一定的黏结力,数量级约为1×10-1MPa,尽管与套管、水泥环所受压力相比较小,但套管-水泥环脱离时必须克服此黏结力。且黏结力与养护时间密切相关,随着养护时间增加,黏结力逐渐增大,但120 h以后变化趋势趋于平稳。本模拟分析中取试验所测最大值0.15 MPa。

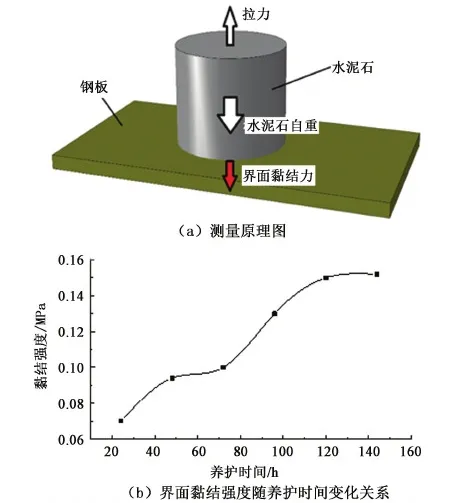
图5 套管-水泥环界面黏结力测量试验原理与结果Fig.5 Schematic diagram and result of casing-cement sheath interface bonding strength measurement experiment

对比Goodwin试验中的载荷施加过程,不同的是模拟分析中设计当套管内压值达到56 MPa并降至0 MPa以后,增加套管内压至14 MPa并降至0 MPa,然后再增加套管内压至69 MPa,最后降低套管内压至0 MPa。模拟结果对比如表2所示。

表2 仿真试验与Goodwin试验结果Table 2 Simulation results and Goodwins experimental results

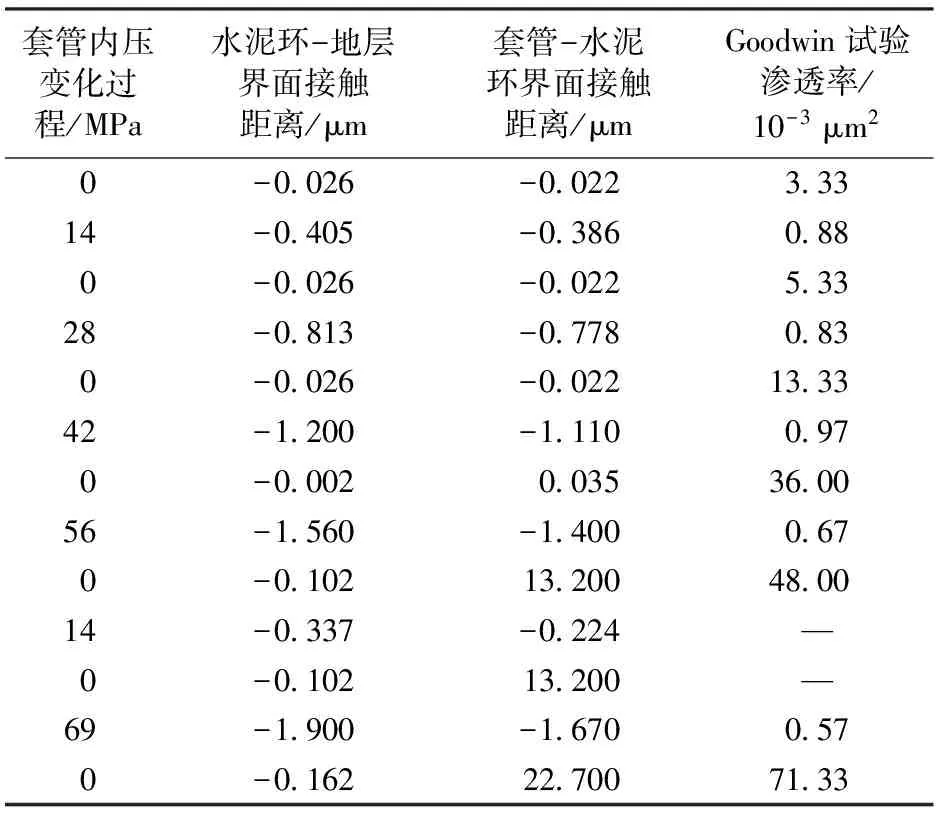
表2 仿真试验与Goodwin试验结果Table 2 Simulation results and Goodwins experimental results

套管内压变化过程/MPa水泥环-地层界面接触距离/μm套管-水泥环界面接触距离/μmGoodwin试验渗透率/10-3μm20-0026-002233314-0405-03860880-0026-002253328-0813-07780830-0026-0022133342-1200-11100970-00020035360056-1560-14000670-010213200480014-0337-0224—0-010213200—69-1900-16700570-0162227007133

从表2中可以看出,模拟分析中增压时界面接触距离为负且近似为0,说明此时界面接触紧密过盈,从增压到55 MPa后再卸压,套管-水泥环界面接触距离为正值,即界面产生了分离,接触距离13.2 μm即为此时微环隙的尺寸。随后增压到14 MPa卸压,微环隙尺寸并未发生变化。但最终增压到69 MPa后再卸压,微环隙尺寸增加到22.7 μm,模拟过程中产生微环隙且套管内压值决定了可能产生的微环隙的尺寸。水泥环-地层界面在整个模拟过程中未产生微环隙,即相同条件下固井一界面比二界面更容易产生微环隙。模拟分析中套管-水泥环界面接触距离变化与试验结果中渗透率变化趋势完全一致,说明Goodwin试验中存在微环隙现象,同时也说明该模拟分析方法具有一定的合理性。

模拟分析中界面接触距离与水泥环内壁等效塑性应变,如表3所示。从表3中可以看出:水泥环内壁初始没有塑性变形,当套管内压增大到42 MPa时,水泥环内壁开始出现塑性变形,但没有产生微环隙;当套管内压增大到56 MPa时,水泥环内壁塑性应变进一步增大,卸压后出现约13.2 μm的微环隙;随后套管内压值没有继续增大而是仅增压到14 MPa,水泥环内壁塑性应变值保持不变,微环隙的尺寸也没有发生变化;当套管内压增加到69 MPa时,水泥环内壁塑性应变进一步增大,卸压后微环隙的尺寸增加到约22.7 μm,由此说明,微环隙的产生和水泥环塑性应变有直接关系,且塑性应变值决定了固井界面微环隙的尺寸。

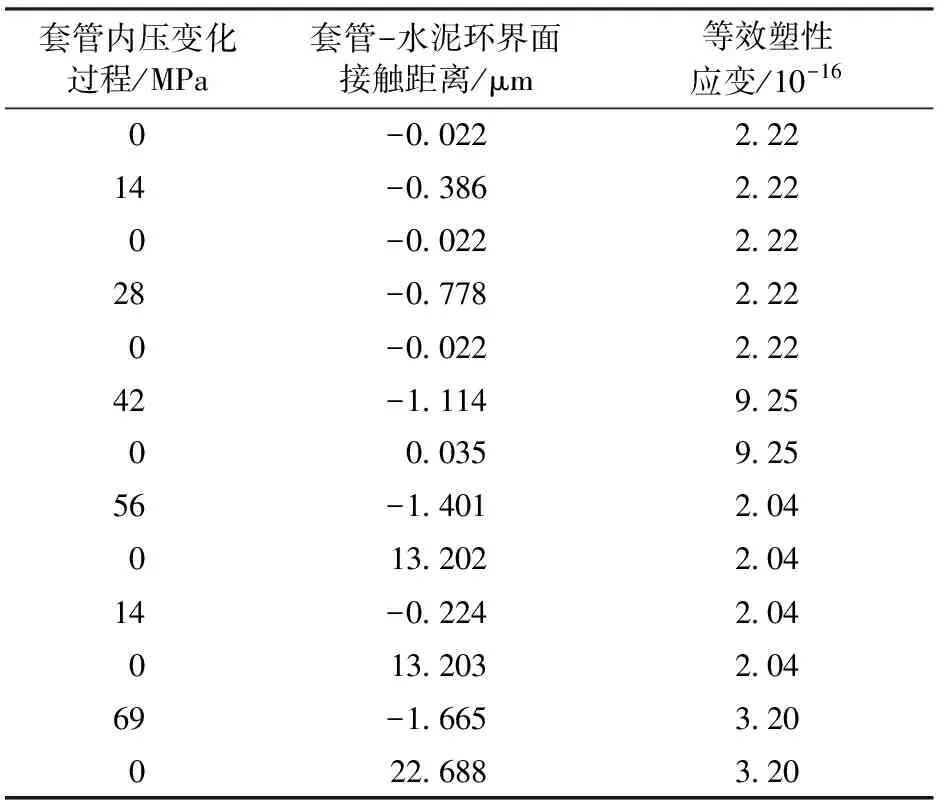
表3 套管-水泥环界面接触距离与水泥环内壁等效塑性应变Table 3 Contact distance and equivalent plastic strain of casing-cement sheath interface

通过以上研究得出固井界面微环隙的产生机制为:套管内压值过大导致水泥环产生塑性变形,当套管内压降低时固井界面将受拉,当该拉应力足以克服界面黏结力时,固井界面会脱离产生微环隙。

2 计算方法

2.1 油气井井筒力学模型建立

套管-水泥环-地层组合体的力学问题可以简化为多层厚壁筒的平面应变问题。假设套管、地层岩石为弹性体,水泥环为理想弹塑性体,满足摩尔-库伦屈服准则,建立如图6所示的套管-水泥环-地层组合体力学模型。

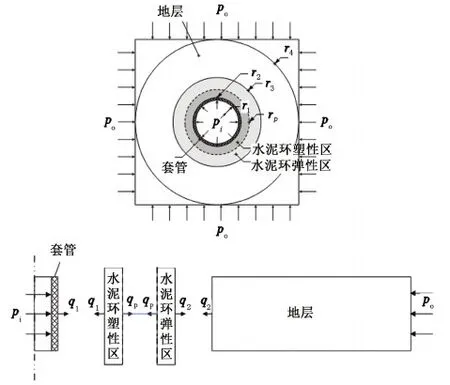
图6 套管-水泥环-地层组合体力学模型Fig.6 Mechanical model of casing-cement sheath-stratum

图6中r1、r2、r3、r4分别为套管内半径、套管外半径、水泥环外半径及地层外半径,rp为水泥环屈服半径,虚线代表水泥环弹塑性区域分界线,pi和po分别为套管内压力和地层外围压力,q1、q2、qp分别为固井一界面、二界面及水泥环弹塑性界面的接触应力,以上作用力都是代数值。

2.2 模型分析求解

首先假设模型中套管、水泥环、地层紧密相连,接触界面满足径向应力和位移连续性条件,且无相对滑动。由于组合体中各部分受力状况类似,故可将套管、地层视为水泥环完全弹性阶段的特殊情况。仅给出水泥环弹塑性状态下的公式推导过程,并利用界面连续性条件求解出组合体各点的应力和位移,推导中应力符号拉为正,压为负。分别用ca、ce、st作为下标表示与套管、水泥环、地层相关的参数。

2.2.1 套 管

由于将套管视为弹性体,位移分量满足拉梅问题的基本解,套管区域径向位移的表达式为

r1≤r≤r2.

(1)

式中,uca为套管径向位移,m;υca为套管泊松比;Eca为套管弹性模量,Pa;r为任意半径,m。

2.2.2 水泥环

当po≥pi时,摩尔-库伦屈服准则满足:

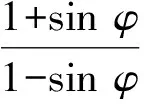
(2)

式中,σθ为周向应力,Pa;σr为径向应力,Pa;φ为内摩擦角,(°);c为黏聚力,Pa。

pi≥po时满足:

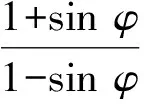
(3)

以po≥pi情况为例,当水泥环内壁应力分布满足式(2)时,水泥环进入弹塑性阶段,此时厚壁筒分为弹性区和塑性区。二者界限为r=rp的圆。应力分量满足二维平面极坐标下的平衡方程:

(4)

将式(2)代入式(4)得

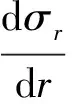
(5)

式(5)为一阶线性偏微分方程,可以用分离变量法求得塑性区域内径向应力分量为

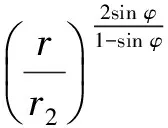
(6)

式中,σrcep为水泥环塑性区径向应力,Pa。

将式(6)代回式(2),可得水泥环塑性区内任一点的周向应力分量为

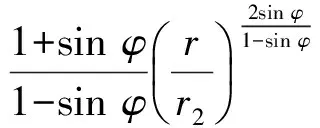
(7)

由式(2)～(6)得在塑性区外边界r=rp处的径向应力为

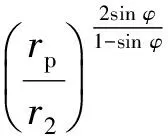
(8)

假设塑性区体积应变为零,则满足:

εm=0或εr+εθ=0.

(9)

其中

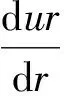
式中,εm为体积应变。

积分得

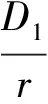
(10)

式中,ucep为水泥环塑性区径向位移,m;D1为积分常数。

水泥环弹塑性交界面处满足位移连续条件ucepr=rp=uceer=rp,可得

(11)

式中,υce为水泥环泊松比;Ece为水泥环弹性模量,Pa。

最终可以得到水泥环塑性区位移的表达式为

(12)

在塑性区以外的弹性区内,其应力状态由外压q2及内压qp共同决定,满足拉梅公式基本解。且当r=rp时满足摩尔-库伦屈服准则,由此可得固井二界面接触力q2的表达式为

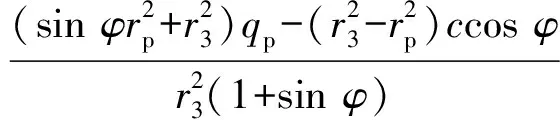
(13)

水泥环弹性区位移分量满足拉梅问题的基本解,可得水泥环弹性区径向位移的表达式为

rp≤r≤r3.

(14)

2.2.3 地 层

将地层视为弹性体,根据拉梅问题的基本解可得地层区域的径向位移表达式为

r3≤r≤r4.

(15)

式中,ust为地层径向位移,m;υst为地层泊松比;Est为地层弹性模量,Pa。

套管、水泥环、地层接触界面满足位移连续性条件,即

(16)

将以上各区域径向位移表达式带入式(16),可得套管内压加载阶段组合体各点的应力和位移。

2.3 固井界面微环隙的产生判别及计算方法

由于在模型中假设套管和地层为弹性体,在套管内压力变化过程中套管和地层的边界位移始终满足拉梅问题的基本解。假设套管内压力卸载到pib时固井一界面接触应力为q1b,固井二界面接触应力为q2b,则套管外壁处径向位移表达式为

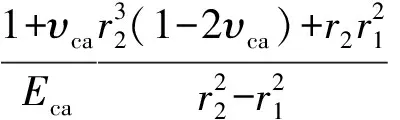
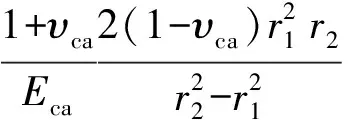
(17)

式中,pib为套管卸压后压力,Pa;ucaob为套管内压为pib时套管外壁径向位移,m;q1b为套管内压为pib时固井一界面接触应力,Pa。

式(17)可以简记为

ucaob=A1q1b-A2pib.

(18)

则地层内壁处径向位移表达式为

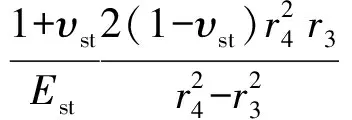
(19)

式中,ustib为套管内压为pib时地层内壁的径向位移,m;q2b为套管内压为pib时固井二界面接触应力,Pa。

式(19)简记为

ustib=A7po-A8q2b.

(20)

另外,假设套管内压卸载前压力为pia,固井一界面接触应力为q1a,固井二界面接触应力为q2a,假设此时水泥环内壁已进入塑性变形阶段,当套管内压降低时,水泥环塑性区域将不再按照原来加载时的应力-应变关系变化,而是存在大小为ucepia的塑性残余变形,则套管内压卸载前后水泥环内壁的径向位移为

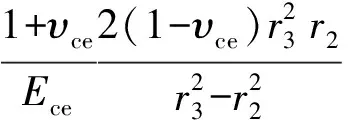
(21)

式中,uceib为套管内压为pib时水泥环内壁径向位移,m;ucepia为套管内压为pia时水泥环内壁塑性位移,m。

将式(21)简记为

uceib=A3(q2a-q2b)-A4(q1a-q1b)-ucepia.

(22)

同理可得套管内压卸载后水泥环外壁的径向位移为

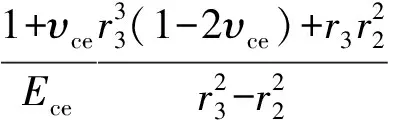
(23)

式中,uceob为套管内压为pib时水泥环外壁径向位移,m;ucepoa为套管内压为pia时水泥环外壁塑性位移,m。

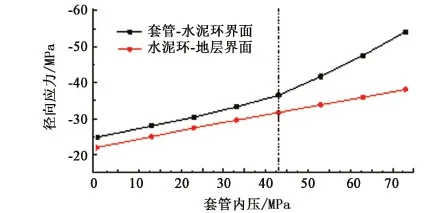
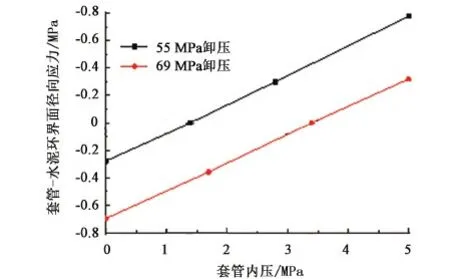
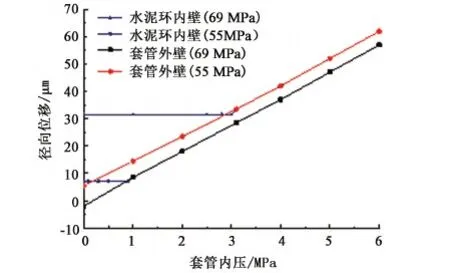
其中,套管内压加载阶段产生的水泥环外壁塑性位移ucepoa只有当rp=r3时存在,若rp

将式(23)简记为

uceob=A5(q2a-q2b)-A6(q1a-q1b)-ucepio.

(24)

假设套管内压力卸载到pib时仍未发生界面脱离,则组合体界面仍满足位移连续性条件,即

(25)

联立公式(18)、(20)、(22)、(24)及式(25)可得套管内压力卸载阶段固井一界面和固井二界面上的接触应力表达式为

q1b=[(A5-A8)(A2pib-ucepia)+A3ucepio+

A3(A7po-A8q2a)+(A3A6-A4A5+A4A8)q1a]/

[(A1-A4)(A5-A8)+A3A6],

(26)

q2b=[(A4-A1)(A7po+ucepio)-A6ucepia+

A2A6pib-A1A6q1a+(A1A5+A3A6-A4A5)q2a]/

[(A1-A4)(A5-A8)+A3A6].

(27)

通过比较固井一界面和二界面理论上的接触应力与界面黏结力判别界面是否产生微环隙,以固井一界面为例,如果发生界面脱开,则组合体将分解为套管、水泥环-地层两个部分,期间套管持续发生弹性变形,由套管压力下降Δpi=pia-pib引起ucaoa-ucaob的套管外壁形变量Δucao,而水泥环-地层区域在脱开前的最终状态是承受界面黏结力c及围压的共同作用,将q1b=c带入式(23)可得到最终状态下水泥环内壁的径向位移表达式为

(28)

套管压力下降Δpi引起的水泥环内壁的形变量为Δucei=uceia-uceib,因此套管压力下降会导致固井一界面脱开,产生尺寸为Δucao-Δucei的微环隙。

3 方法验证

利用所建立的固井界面微环隙的计算方法对有限元模拟试验进行计算。并通过对比结果对计算方法的合理性进行验证。计算中所采用的参数同有限元模拟试验(表1)。套管内压为0～69 MPa,远场地应力为34.84 MPa。对有限元模拟试验中套管内压分别增加到56、69 MPa后卸压至0 MPa有微环隙产生的过程进行计算,计算结果如图7、8所示,其中负为压应力,正为拉应力。

图7 内压加载时固井界面应力变化曲线Fig.7 Change of interfacial stress with casing pressure loading

图8 内压卸载时固井一界面应力变化曲线Fig.8 Change of interfacial stress with casing pressure unloading

从图7中可以看出,加载阶段随着套管内压值的升高,固井一、二界面上的接触应力均呈上升趋势,但一界面应力始终大于二界面应力。该加载条件下套管内压值超过43 MPa(前文有限元模拟试验中为42 MPa)时,水泥环从固井一界面开始进入塑性阶段,但整个加载过程中,水泥环仅部分发生塑性变形,且固井二界面未进入塑性阶段,因此该过程中固井一界面可能产生微环隙,固井二界面不会产生微环隙。

图8为套管内压卸载阶段的固井一界面接触应力的变化曲线。从图8中可以看出,随着套管内压的降低,固井一界面上的接触力逐渐减小。套管内压从55 MPa卸载时,卸载到1.4 MPa时界面接触力由压应力转变为拉应力,当套管内压卸载到0 MPa时产生0.28 MPa的拉应力;套管内压从69 MPa卸载时,卸载到3.4 MPa时界面接触力同样变为拉应力,且当套管内压为0 MPa时界面上的拉应力达到0.7 MPa。

以上两阶段套管内压卸载到0 MPa时所产生的界面拉应力均超过了实测的套管-水泥环界面黏结力0.15 MPa,可以假设该两阶段均产生了微环隙。可利用本文中所建立的微环隙的计算方法对微环隙尺寸进行计算,结果如图9所示。

图9 固井一界面微环隙尺寸计算结果Fig.9 Calculation result of casing-cement sheath interface micro-annulus

从图9中可以看出,套管内压分别从55和69 MPa卸载时,随着套管内压值的减小,初始阶段套管外壁和水泥环内壁位移一致,即套管和水泥环协同变形收缩,且固井界面始终保持连接。当套管内压分别卸载到1和3.1 MPa时,由于界面所产生的拉应力足以克服0.15 MPa的界面黏结力,界面将脱开。之后套管将继续进行弹性收缩直至原始状态,而水泥环由于最终所承受的界面黏结力和围压的共同作用,将在产生少量的收缩后位移不再变化。由于加载阶段界面位移始终连续相等,对比卸载后最终状态时套管外壁和水泥环内壁的位移差即可得到该加载卸载工况下微环隙的尺寸。图9中,套管内压从55和69 MPa卸载后,固井一界面分别产生了10.5和23.9 μm的微环隙。该计算结果与前文的有限元模拟试验结果较为一致,说明该计算方法合理、精确,且印证了Goodwin试验结果中存在微环隙且造成环空渗透率大幅增加的现象。

4 结 论

(1)固井界面微环隙的产生机制为:套管内压值过大导致水泥环产生塑性变形,而当套管内压降低时固井界面将受拉,当该拉力足以克服界面黏结力时,固井界面将会脱离产生微环隙。

(2)套管-水泥环间存在黏结力,测定数量级大约为0.1 MPa,且黏结力与养护时间密切相关,随着养护时间增加,黏结力逐渐增大,但120 h以后变化趋于平稳。

(3)建立了固井界面微环隙的理论计算方法,计算结果与有限元模拟结果具有很好的一致性,说明该方法具有较高的精度。利用该方法可以对油气井服役过程中的井筒密封完整性状态进行预测,指导试压、试采及压裂等工艺措施的设计和现场施工,有效降低井筒密封完整性失效风险。

[1] BOUKHELIFA L, MORONI N, JAMES S G, et al. Evaluation of cement systems for oil and gas well zonal isolation in a full-scale annular geometry[J]. SPE Drilling & Completion, 2013,20(1):44-53.

[2] DEREMBLE L, LOIZZO M, HUET B, et al. Assessment of leakage pathways along a cemented annulus[R]. SPE 139693-MS, 2010.

[3] 赵效锋,管志川,廖华林,等.水泥环力学完整性系统化评价方法[J].中国石油大学学报(自然科学版),2014,38(4):87-92.

ZHAO Xiaofeng, GUAN Zhichuan, LIAO Hualin, et al. Systemic evaluation method of cement mechanical integrity[J].Journal of China University of Petroleum(Edition of Natural Science), 2014,38(4):87-92.

[4] GRAY K E, PODNOS E, BECKER E. Finite element studies of near-wellbore region during cementing operations: part I[J]. SPE Drilling & Completion, 2007,24(1):127-136.

[5] GOODWIN K J, CROOK R J. Cement sheath stress failure [J]. SPE Drilling Engineering, 1992,7(4):291-296.

[6] JACKSON P B, MURPHEY C E. Effect of casing pressure on gas flow through a sheath of set cement [R].SPE/IADC 25698, 1993.

[7] HEATHMAN J F, BECK F E. Finite element analysis couples casing and cement designs for HTHP wells in East Texas[R]. SPE 98869-MS, 2006.

[8] 姚晓,周兵,李美平,等.套管试压对水泥环密封性的影响[J].西安石油大学学报(自然科学版),2009,24(3):31-34.

YAO Xiao, ZHOU Bing, LI Meiping, et al. Effect of casing pressure testing on the sealing performance of cement sheath[J]. Journal of Xian Shiyou University(Natural Science Edition),2009,24(3):31-34.

[9] 陈勇,练章华,许树谦,等.热采井蒸汽吞吐过程形成的一界面微间隙计算[J].石油机械,2009,37(2):22-24.

CHEN Yong, LIAN Zhanghua, XU Shuqian, et al. Calculating first interface micro-annulus width during steam stimulation in thermal recovery well[J]. China Petroleum Machinery,2009,37(2):22-24.

[10] 万曦超.油气井固井水泥环力学研究[D].成都:西南石油大学, 2006.

WAN Xichao. Study on cement sheath mechanics of well cementing[D]. Chengdu: Southwest Petroleum University, 2006.

[11] 刘骁,田野,李明亮,等.变内压下套管与水泥环微间隙研究[J].重庆科技学院学报(自然科学版),2009,11(5):56-58.

LIU Xiao, TIAN Ye, LI Mingliang, et al. Micro-clearance study between casing and cement annulus under swing pressure[J]. Journal of Chongqing University of Science and Technology(Natural Sciences Edition),2009,11(5):56-58.

[12] 初纬, 沈吉云, 杨云飞,等. 连续变化内压下套管-水泥环-围岩组合体微环隙计算[J]. 石油勘探与开发, 2015,42(3):379-385.

CHU Wei, SHEN Jiyun, YANG Yunfei, et al. Calculation of micro-annulus size in casing-cement sheath-formation system under continuous internal casing pressure change[J]. Petroleum Exploration and Development, 2015,42(3):379-385.

[13] 赵效锋,管志川,廖华林,等.交变压力下固井界面微间隙产生规律研究[J].石油机械,2015,43(4):22-27.

ZHAO Xiaofeng, GUAN Zhichuan, LIAO Hualin, et al. Study on cementing interface micro-annulus generation rules under alternating casing pressure[J]. China Petroleum Machinery, 2015,43(4):22-27.

(编辑 李志芬)

Anassessmentmethodforoccurrenceofmicro-annularfracturesoncementinginterfacesofoilandgaswellcasing

ZHAO Xiaofeng1,2, GUAN Zhichuan1, SHI Yucai1, LI Tao1, LIAO Hualin1, JIANG Jinxing1, SUN Baojiang1

(1.SchoolofPetroleumEngineeringinChinaUniversityofPetroleum,Qingdao266580,China; 2.ResearchInstituteofPetroleumEngineering,ZhongyuanOilfieldCompany,SINOPEC,Puyang457001,China)

The generation and development of micro-annular fractures on cementing interface of oil and gas well casing during long-term production were investigated via simulation experiments, and the bonding strength of cementing interface was measured in the experiments. Based on the experimental results, a theoretical assessment method of the micro-annular fracture was developed, and a good agreement between the experimental results and modeling was observed. The results show that an excessive inner casing pressure can lead to plastic deformation of cement sheath, while a tensile stress can be subjected on the cementing interface when the inner pressure is reduced during the casing pressure unloading process. The magnitude of the interfacial bonding strength is of 0.1 MPa as it was measured in the experiments, and micro-annular fractures can appear at the cementing interfaces when the tensile stress is sufficient high to overcome the bonding strength. The larger the inner casing pressure, the higher probability for the micro-annular fractures to occur during pressure surge, and the larger the fractures. Micro-annular fractures are more likely to appear at the first casing-cement interface due to a higher tensile stress even if the bonding strength at two interfaces is the same.

well integrity; micro-annular fracture; simulation experiment; theoretical calculation; bonding strength

2016-12-08

国家自然科学基金项目(51674284);中央高校基本科研业务费专项(R1502039A, 16CX06035A)

赵效锋(1987-),男,博士,研究方向为油气井力学、深井超深井钻井及井筒完整性管理。E-mail:zhaoxiaofeng_upc@163.com。

管志川(1959-),男,教授,博士,博士生导师,研究方向为油气井力学、井下测控技术、深井超深井钻井和深水钻井。E-mail:guanzhch@upc.edu.cn。

1673-5005(2017)05-0094-08

10.3969/j.issn.1673-5005.2017.05.011

TE 21

A

赵效锋,管志川,史玉才,等.固井界面微环隙产生机制及计算方法[J].中国石油大学学报(自然科学版),2017,41(5):94-101.

ZHAO Xiaofeng, GUAN Zhichuan, SHI Yucai, et al. An assessment method for occurrence of micro-annular fractures on cementing interfaces of oil and gas well casing[J].Journal of China University of Petroleum(Edition of Natural Science),2017,41(5):94-101.