纳卫星变轨段质量矩姿态控制系统设计
陆正亮, 张翔, 于永军, 莫乾坤, 廖文和
南京理工大学 机械工程学院, 南京 210094
纳卫星变轨段质量矩姿态控制系统设计
陆正亮, 张翔*, 于永军, 莫乾坤, 廖文和
南京理工大学 机械工程学院, 南京 210094
提出应用质量矩控制技术实现纳卫星轨道机动过程中的姿态稳定控制。在设计出质量矩滑块构型后,利用动量和动量矩定理推导了八自由度(DOF)动力学模型,并根据动力学分析结果建立了简化控制模型。以此为基础,基于全局滑模控制理论设计了俯仰偏航通道姿态稳定和滑块位置跟踪的鲁棒控制器,并在参数不确定性条件下对控制系统进行了仿真,结果表明:所设计的二维质量矩控制系统能快速控制卫星姿态,并对系统扰动具有较强的鲁棒性,可以应用于纳卫星变轨段的姿态控制。
变轨; 纳卫星; 质量矩; 姿态控制; 滑模控制
随着信息技术与小型化技术的飞速发展,纳卫星在空间科学领域展现出了勃勃生机,同时对纳卫星平台的轨道机动能力的需求日益增长[1]。常用于卫星轨道机动任务的推进系统主要有液体推进和固体推进等,推进系统的推力矢量偏差以及卫星本体的质心偏差容易导致卫星姿态发生偏转,必须对卫星姿态进行自旋稳定控制或三轴主动控制[2-3]。通常姿态三轴主动控制采用喷气、角动量控制以及磁控方式,其中角动量控制及磁控吸收扰动力矩的能力有限,故常使用多喷嘴小推力的姿控发动机对变轨机动过程中的姿态进行调整[4],但其复杂的系统应用到纳卫星上成本较高且有一定难度。本文提出一种应用质量矩控制技术调整纳卫星姿态的方法并对其可行性进行分析。
质量矩控制通过调整内部滑块间相对位置使系统质心发生变化,改变外力的作用力臂从而产生相应的附加力矩控制飞行器姿态运动。目前为止国内外学者研究质量矩技术的载体主要是再入弹头和动能拦截弹[5]。在再入弹头领域主要研究了单滑块或双滑块配置对自旋弹头弹道变化的影响[6-7],如美国海军水面战研究中心的Regan和Kavetsky设计的一种单自由度活动质量体配平控制器[8],能够在再入弹头接近目标时对弹道做适度的修正以提高制导精度;Petsopoulos等对单自由度质量体控制再入弹头的滚动问题进行了详细研究[9]。在动能拦截弹领域主要针对非自旋拦截弹[10-11],如Menon等重点研究了质量矩拦截弹制导控制一体化设计问题,并对拦截弹在大气层外和大气层内打击目标的情况进行了仿真[12]。中国西北工业大学周凤岐老师[13-15]和哈尔滨工业大学荆武兴老师[16-18]的科研团队等也对质量矩技术进行过系统研究。
质量矩控制技术应用在卫星姿态控制时与再入弹头或反导拦截器不同。在卫星变轨机动时作用在卫星上的主动力主要是发动机产生的固定或可变推力,而再入弹头或反导拦截器上作用的是与姿态相关的气动外力;质量矩应用于卫星姿态控制的目的是稳定姿态,而应用在弹头和拦截弹时则是通过配平气动力矩达到控制攻角的目的。
有部分学者研究过卫星的质量矩姿态控制技术,文献[19-20]提出了使用活动质量块改变整星惯性张量从而调整卫星姿态的方法,但由于没有尾部推力作用使得系统响应较慢,这种控制机理本质已经不属于质量矩控制的范畴。文献[21]提出使用四根可摆动质量杆来调整整星质心从而达到补偿固体推进器推力矢量偏差的目的,但并没有对方案进行详述且这种构型设计未考虑与分离机构干涉的问题,不利于后期进行工程化应用。
本文以进行变轨机动的双单元立方体卫星为平台对卫星质量矩姿态控制技术进行分析研究,研究重点为质量矩构型配置、质量矩建模、控制机理分析以及质量矩控制律。
1 质量矩卫星的动力学模型
1.1 滑块配置
质量矩飞行器的滑块配置构型常采用单滑块、双滑块以及三滑块构型。本文针对变轨机动的立方星初步设想的滑块配置参见图1所示,整个系统由卫星本体和二维可移动滑块组成。图1中OBXBYBZB为卫星本体坐标系;OIXIYIZI为地心惯性坐标系;T为本体系下描述的发动机推力,理想情况下的发动机推力沿卫星本体系XB轴方向;rT为发动机推力作用点在卫星本体系中的位置;OS为系统质心;G为整个卫星系统受到的地心引力矢量;py和pz为活动质量块在本体系下的坐标;ωx、ωy和ωz为卫星本体沿3个方向的自转角速率。下面初步分析此构型是否满足卫星轨道机动过程中的姿态控制。

图1 质量矩卫星的滑块配置Fig.1 Actuator configuration of satellite mass moment system
空间飞行器的简化轨道动力学基本方程为
(1)
式中:r为地心至卫星本体质心的位置矢量;r为r的模值;G为地球引力常数;m为星体质量;Aoi和Abo分别为轨道系到惯性系以及本体系到轨道系的坐标转换矩阵。当控制俯仰角以及偏航角为小量时Abo·T可表示为
(2)
式中:T为设计的发动机推力大小,由式(2)可见滚动角φ的大小并不影响卫星变轨机动的过程。再来分析推力偏心力矩的组成。发动机的推力偏心力矩M是由发动机推力误差[δTxδTyδTz]T以及相对于卫星质心的作用力臂误差[δrxδryδrz]T造成的,引入误差项后得到发动机推力偏心力矩为
(3)
由式(3)可知,当各轴误差量级相同的情况下,在滚动通道的推力偏心力矩相对俯仰偏航通道来说为小量。故质量矩控制系统的任务只需要控制俯仰偏航角即可,图1中设计的沿YB轴运动滑块控制偏航角,沿ZB轴运动滑块控制俯仰角,可以满足系统任务需求。
1.2 八自由度完整动力学模型
建模中用到的符号说明如下:
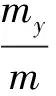

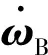
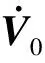
5) 矩阵Abi为卫星本体系到地心惯性系的坐标转换矩阵。
7)IB为卫星除去活动质量块外的相对质心OB的惯性张量。
8)Fp和Mp为卫星系统在本体系下受到空间环境的干扰力及力矩,来源于气动、剩磁、太阳光压等扰动。
分析1.1节滑块布局可知整星具有8个自由度,即整星三维平动、三维转动以及二维滑块的直线运动。故完整动力学方程应该包括:系统三维平动动力学方程、绕质心三维转动动力学方程以及二维滑块平动动力学方程。
首先在惯性系下应用质点系动量定理得到三维平动动力学方程:
Abi·(T+Fp)+G
(4)
对本体质心OB点运用质点系动量矩定理得到三维转动动力学方程如式(5)所示。二维滑块平动动力学方程描述如式(6)和式(7)所示。式(6)和式(7)中by=[0 1 0],bz=[0 0 1],uy和uz是伺服机构施加给滑块的主动控制力矩。式(4)~式(7)共同组成了质量矩控制系统的八自由度完整动力学方程:
[mypy×(ωB×py)+mzpz×(ωB×pz)]+
(5)
(6)
(7)
1.3 姿态运动学方程
当控制卫星的姿态欧拉角均为小角度时,卫星的姿态运动学方程可描述为
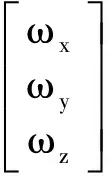
(8)
式中:ψ为偏航角;θ为俯仰角;ωo为轨道角速率。
1.4 姿态控制模型分析
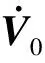
Mk+Mg+Mp-(μypy+μzpz)×Fp
(9)
式中:
ΔI=my·Tensor(py)+mz·Tensor(pz)
Mc=(rT-Δr)×T

式(9)中ΔI为附加转动惯量,由展开式(10)可知,由于活动质量块的位置变化引入了附加转动惯量ΔI,使系统惯性主轴发生了偏移,轴间耦合加剧;但设置滑块安装偏移量δx、δy和δz均为0时,可见ΔI仅存对角线元素,表明此时滑块运动并不会引起通道间耦合,但还是会给主轴惯量引入一定误差。
式(9)中Mc为推力外力矩,结合式(3)可知质量矩控制技术就是通过调整Δr大小来调整姿态的,略去高阶项及小量后并展开Mc可得式(11)。
式(11)中Tx、Ty和Tz为发动机矢量的三轴分量;Txδrz+0.1Tz和-0.1Ty-Txδry为发动机的推力矢量偏差力矩在YB轴和ZB轴的分量;同时由于质量块的安装位置偏差在俯仰轴和偏航轴分别引入了较大的常值力矩-Txμyδz和Txμzδy,这会对活动质量块的控制能力产生很大影响,需要在卫星质心配平时将其抵消掉;-Txμzlz和Txμyly为活动质量块位置决定的控制力矩,由此可见ZB轴质量块的位置lz可以用来控制卫星俯仰轴姿态稳定,而YB轴质量块的位置ly可以用来控制卫星偏航轴姿态稳定,且任一活动质量块的运动不会对其他通道产生干扰,这是应用质量矩控制技术实现卫星姿态控制的机理所在。
式(9)中的附加惯性力矩Ma是由于活动质量块运动时产生的惯性力对系统型心形成的力矩,其展开式如式(12)所示。可见质量块纵向安装偏差δx是引起俯仰和偏航轴附加惯性力矩的主要原因,当δx设置为0时,俯仰和偏航轴附加惯性力矩即为0。
式(9)中的附加哥氏力矩Mk是由活动质量块运动与卫星姿态运动耦合产生的,其俯仰轴和偏航轴的分量展开式如式(13)和式(14)所示。观察展开式可发现,活动质量块的安装位置是影响附加惯性力矩大小的主要因素,当设计安装位置δx、δy、δz均为0时,附加惯性力矩在偏航和俯仰通道上的分量大小均大幅减小。
式(9)中Mg是质量块上的离心力所产生的附加陀螺力矩,其表达式较为复杂,这里不便展开书写,但其与附加哥氏力矩类似,当设计安装位置δx、δy和δz均为0时,附加陀螺力矩将大幅减小。另外式(9)中的Mp-(μypy+μzpz)×Fp为空间环境的外干扰力矩,包括气动力矩、光压力矩和剩磁力矩等,参考文献[22]可知空间环境的外干扰力矩大小量级为10-6,远小于上述其他的干扰力矩,故在此不作详细展开分析。
从式(12)~式(14)可见影响附加扰动力矩Ma、Mk和Mg大小的因素主要有滑块质量,卫星角速度,以及滑块的安装位置δx、δy和δz;滑块质量大小的选择由质量矩控制系统的能力需求决定,而卫星角速度大小与最终的控制系统性能有关,只有滑块的安装位置是可以通过优化设计来减小扰动力矩的大小,从而提高质量矩控制系统性能。
(10)
(11)
(12)
(13)
(14)

图2 δx不同时引入的扰动力矩大小Fig.2 Magnitude of importing disturbance torque with different δx
由上述扰动力矩Ma、Mk和Mg的展开式分析可知,当安装位置δx、δy、δz均为0时,由质量块运动导致的附加扰动力矩最小。如图2、图3所示,采用数值仿真的方法可以来验证上述结论,仿真参数与第4节中的相关参数相同,只是这里滑块运动采用设计好的正弦运动,运动周期为0.4 s,幅值为0.02 m,仿真时间为0.1 s图中横坐标为仿真时间,纵坐标为扰动力矩Ma、Mk、Mg的和。

图3 δy、δz不同时引入的扰动力矩大小Fig.3 Magnitude of importing disturbance torque with different δy and δz
由图2可见当δx=0时俯仰轴和偏航轴的扰动力矩分量最小,且随着质量块的纵向安装位置越偏离质心引入的扰动力矩越大,但纵向安装位置并不影响滚动轴的扰动力矩大小。由图3可见当δy=0、δz=0时各轴的扰动力矩均较小,相对其他3种布局方式这种构型的扰动力矩大约小一个数量级左右。结果表明当δx、δy和δz均为0时,扰动力矩最小,此时控制系统的动态品质最优,也与上述的理论分析结果相吻合。
2 控制模型
2.1 姿态控制简化模型
设计布局参数δx、δy和δz均为0,此时代入姿态运动学方程并忽略掉高阶小量后得到姿态控制方程为
(15)

2.2 质量块位置控制简化模型
结合系统三维平动动力学方程式(4)和滑块平动动力学方程式(6)和式(7)可得
(16)
式中:Tdz和Tdy为卫星本体施加给质量块的附加惯性力,是控制滑块位置的扰动因素,其展开式如式(17)和式(18)所示,在俯仰姿态小角度情况下Tdz和Tdy大小存在上限。
(17)
(18)
2.3 双回路控制
[23]将质量矩控制系统分成两部分:一是姿态稳定控制回路,二是滑块位置伺服控制回路,完整的质量矩控制系统的控制流程图如图4所示。图中理想的俯仰和偏航姿态角均为0°,由姿态传感器实时测量卫星姿态角及角速度并送入质量矩姿态控制器,计算得到理想的滑块位置;再由滑块位置传感器测量实时位置速度并送入滑块位置控制器,计算得到施加于滑块的驱动力,至此完成双回路闭环控制。图4中上标^均表示测量系统输出的状态估计值。

图4 质量矩控制系统控制原理图Fig.4 Block diagram of mass moment control system
3 滑模控制器设计
由第2节控制模型分析可知,在姿态控制回路和滑块位置控制回路中都存在由于滑块运动引起的扰动力和扰动力矩,导致系统呈现较强的非线性特征,本文采用滑模控制器来设计质量矩鲁棒控制系统。在设计控制器时假设系统状态全维可观测。
由于传统的滑模控制器对系统参数不确定性以及外部扰动的鲁棒性仅存在于滑动模态阶段,这里尝试通过设计一种动态非线性滑模面来实现全局滑模控制,避免由于系统状态方程的强扰动和强非线性导致控制发散。
3.1 姿态稳定滑模控制器设计
针对俯仰轴姿态控制系统,将式(15)中俯仰通道控制方程简写为
(19)

(20)

(21)
设计控制律为
sgn(s1)-ε1s1
(22)

(23)
则有
(24)
由B和ΔB的定义,式(24)中存在以下关系:

(25)

3.2 滑块位置跟踪滑模控制器设计
对于ZB轴方向滑块的位置控制,其模型可以简写为
(26)

(27)

(28)
设计控制律为
(29)
式中:ε2为指数趋近律参数,定义Lyapunov函数为
(30)
则有
(31)
可见设计的控制律能使状态轨迹沿着设计的滑模面趋近至零;为了降低抖振,可采用饱和函数代替符号函数。YB轴滑块控制器设计与ZB轴滑块类似。
4 仿 真
为验证质量矩系统在变轨机动过程中的有效性,使用MATLAB搭建质量矩控制系统数值仿真平台。仿真以一颗2.36 kg的立方体卫星使用固体火箭发动机由500 km圆轨道到300 km×500 km椭圆轨道的变轨任务为背景,通过计算可得变轨所需速度增量为-56 m/s,选用的推力器为固体火箭推力器,推力大小为30 N,工作时间为 4.4 s;质量矩系统中卫星本体的质量为1.8 kg,两个活动质量块的质量均为0.28 kg;卫星本体惯性张量为diag(0.003,0.008,0.008) kg·m2;初始姿态角为[1° -1° 1°],角速率为[-0.01 0.01 -0.01] (°)/s;发动机推力矢量偏差参考文献[21]中通过工程统计所得出的数据,推力T=[30 0.1 0.1] N,rT=[-0.1 0.001 0.001] m;限于立方体卫星的结构尺寸的大小,质量块运动最大行程设置为0.03 m;影响质量矩控制系统响应性能的是驱动质量块运动的直线电机的驱动力大小,驱动力越大,则质量块的位移变化越快,质量矩控制系统的动态响应特性也就越好,这里选型的直线电机型号为Faulhaber LM 0830,其最大驱动能力为1 N。
仿真过程中空间环境的干扰力及力矩较发动机推力及推力偏心力矩大小而言小数个数量级,故在仿真中不予考虑。
对于滑模控制器参数,计算可得B和ΔB分别为-0.002 7和2.9×10-5;b2为6.2;c1和c2分别取为5和50;D1和D2取为10和20;ε1和ε2均取为5;使用饱和函数代替符号函数,饱和函数的边界层大小均设为0.05;函数f1(t)和f2(t)的参数k1和k2均取为-50。初步仿真结果如图5~图8所示。
图5为在施加推力偏心力矩的情况下使用质量矩控制达到的姿态控制效果,可见偏航俯仰通道在1 s左右能稳定下来;偏航角和俯仰角分别有一个4° 和2.6° 的超调;滚动通道在发动机工作结束后仅有1.5° 的偏差,证实了第1节的部分理论计算结果;同时偏航俯仰两通道均存在一个0.3° 左右的稳态误差,这是由于控制系统存在一定模型误差以及推力偏心外扰动造成的,虽然可以通过增大控制系统的增益值来减小稳态误差,但势必会造成超调增大、执行机构过载等情况出现,故需综合考虑。
图6所示为卫星轨道坐标系下的4条X轴速度变化曲线,其中实线代表未进行变轨机动,短虚线代表理想中的轨道机动,即发动机不存在推力偏心力矩,长虚线代表未进行姿态控制的轨道机动,点划线表示轨道机动时使用了本文的质量矩控制技术。图中可见未进行姿态控制的轨道机动会由于姿态翻转而在原地“打转”,导致变轨失败。而短虚线与点划线基本重合说明使用质量矩技术控制卫星姿态达到了变轨目的,且在变轨结束后X轴速度与理想值仅偏差0.04 m/s,变轨精度较高。

图5 质量矩控制下的姿态变化曲线Fig.5 Curve of attitude with mass moment control

图6 轨道坐标系下的X轴速度变化曲线Fig.6 Curve of X axis velocity in orbit coordinate system
图7和图8分别表示质量矩控制过程中的滑块位置和滑块驱动力的变化,由于仿真假定的推力矢量偏差为常值扰动,相当于给控制系统输入了一个阶跃扰动,因此在卫星姿态稳定下来之后滑块位置和驱动力均不再变化。由图可知设计的滑块运动最大行程以及选型的执行机构的驱动能力均可以满足本文设计的质量矩姿态控制系统需求。事实上,质量块质量比、最大运动行程和最大驱动力是衡量质量矩控制系统能力的主要指标,但这些参数的选取需要综合多方面的因素,比如质量块行程加大可能导致定位精度变差、质量比加大导致引入控制系统的扰动力矩增大等,因此需要结合实测的发动机推力矢量偏差大小来倒推质量矩控制系统的能力需求,从而设计出合理的系统参数以及选出适用的执行机构。

图7 滑块位置变化曲线Fig.7 Curve of position of actuator masses
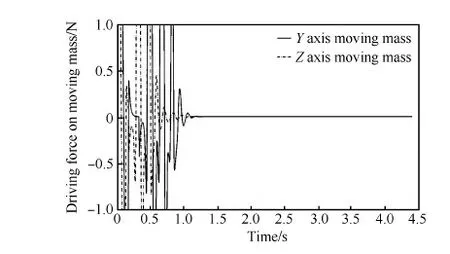
图8 滑块驱动力变化曲线Fig.8 Curve of driving force of actuator masses
5 结 论
1) 在有外力作用时使用质量矩控制技术实现姿态控制是可行的,且二维滑块分别控制俯仰和偏航轴的滑块配置方案是合理的。
2) 在滑块安装布局上设置偏移量δx、δy和δz均为0,可使得系统避免俯仰偏航通道上的动力学耦合,同时可大幅降低滑块运动带来的扰动力矩。
3) 设计的双回路全局滑模控制器使得系统在响应的全过程都具备了鲁棒性,数值仿真也验证了控制器的有效性。
4) 发动机的推力矢量偏差特性对质量矩姿态控制系统的设计至关重要,在实际工程应用中需对其精确测量。
参 考 文 献
[1] RHEE M S, ZAKRZWSKI C M, THOMAS M A. Highlights of nanosatellite propulsion development program at NASA-Goddard Space Flight Center[C]//Proceedings of 14th Annual AIAA/USU Small Satellite Conference. Utah: Utah State University, 2000.
[2] 吕振铎. 轨道机动期间的姿态控制[J]. 中国空间科学技术, 1994(5): 25-30.
LV Z D. Attitude control during orbit maneuver[J]. Chinese Space Science and Technology, 1994(5): 25-30 (in Chinese).
[3] 李雯, 肖凯. 变轨发动机工作态主动式自旋稳定姿态控制[J]. 宇航学报, 2004, 25(2): 231-234.
LI W, XIAO K. Active attitude control for a spin-stabilized spacecraft while the orbit transform motor is working[J]. Journal of Astronautics, 2004, 25(2): 231-234 (in Chinese).
[4] 张钊, 胡军. 轨道机动时考虑延迟的卫星姿态稳定控制方法[J]. 宇航学报, 2011, 32(2): 290-296.
ZHANG Z, HU J. Satellite attitude stabilization with time delay during orbital maneuver[J]. Journal of Astronautics, 2011, 32(2): 290-296 (in Chinese).
[5] 高长生, 李君龙, 荆武兴, 等. 导弹质量矩控制技术发展综述[J]. 宇航学报, 2010, 31(2): 307-314.
GAO C S, LI J L, JING W X, et al. Key technique and development for moving mass actuated kinetic missile[J]. Journal of Astronautics, 2010, 31(2): 307-314 (in Chinese).
[6] WHITE J E, ROBINETT R D. Principal axis misalignment control for deconing of spinning spacecraft[J]. Journal of Guidance, Control, and Dynamics, 1994, 17(4): 823-830.
[7] BYRNE R H, STURGIS B R, ROBINETT R D. A moving mass trim control system for reentry vehicle guidance: AIAA-1996-3438[R]. Reston: AIAA, 1996.
[8] REGAN F J, KAVETSKY R A. Add-on controller for reentry vehicles: U.S., Serial No.752766[P]. 1984.
[9] PETSOPOULOS, REGAN F J, BARLOW J. Moving mass control system for fixed-trim reentry vehicle[J]. Journal of Spacecraft Rockets, 1996, 33(1): 54-60.
[10] VADDI S S, MENON P K, SWERIDUK G D. Multi-stepping solution to linear two point boundary value problems in missile integrated control[C]//Proceedings of AIAA Guidance, Navigation and Control Conference. Reston: AIAA, 2005.
[11] VADDI S S, MENON P K, SWERIDUK G D. Multistepping approach to finite-interval missile integrated control[J]. Journal of Guidance, Control and Dynamics, 2006, 29(4): 1015-1019.
[12] MENON P K, SWERIDUK G D, OHLMEYER E J. Integrated guidance and control of moving-mass actuated kinetic warheads[J]. Journal of Guidance, Control and Dynamics, 2004, 27(1): 118-126.
[13] 周凤岐, 易彦, 周军. 克服旋转导弹螺旋运动的方法研究[J]. 宇航学报, 2001, 22(5): 77-81.
ZHOU F Q, YI Y, ZHOU J. Research on overcoming the coning motion of rotary missile[J]. Journal of Astronautics, 2001, 22(5): 77-81 (in Chinese).
[14] 易彦, 周凤岐, 余松煜. 变质心控制导弹的稳定性分析与鲁棒控制[J]. 上海交通大学学报, 2003, 37(4): 570-573.
YI Y, ZHOU F Q, YU S Y. Analysis on stability of variable centroid controlled missile and robust control[J]. Journal of Shanghai Jiaotong University, 2003, 37(4): 570-573 (in Chinese).
[15] 何珺, 周凤岐, 周军. 变质心控制导弹H∞综合LPV鲁棒自动驾驶仪的设计[J]. 西北工业大学学报, 2004, 22(3): 360-364.
HE J, ZHOU F Q, ZHOU J. On using moving-mass-centerH∞control for simplifying design of LPV missile autopilot[J]. Journal of Northwestern Polytechnical University, 2004, 22(3): 360-364 (in Chinese).
[16] 高长生, 荆武兴, 于本水, 等. 质量矩导弹构型及自适应控制律设计[J]. 航空学报, 2010, 31(8): 1593-1599.
GAO C S, JING W X, YU B S, et al. Configuration and adaptive control law design for a mass moment missile[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(8): 1593-1599 (in Chinese).
[17] 李瑞康, 荆武兴, 高长生, 等. 变质心飞行器姿态与弹道性能分析[J]. 宇航学报, 2009, 30(4): 1498-1503.
LI R K, JING W X, GAO C S, et al. Performance analysis of attitude and ballistic for moving mass actuated vehicle[J]. Journal of Astronautics, 2009, 30(4): 1498-1503 (in Chinese).
[18] 魏鹏鑫, 高长生, 荆武兴. 基于稳定性分析的变质心再入飞行器布局参数设计[J]. 导弹与航天运载技术, 2012(1):34-39.
WEI P X, GAO C S, JING W X. Research on the method of layout parameter design for moving mass actuated reentry vehicle based on stability analysis[J]. Missiles and Space Vehicles, 2012(1): 34-39 (in Chinese).
[19] YOUNG T A. Attitude dynamics and control of a spacecraft using shifting mass distribution[D]. Pennsylvania: The Pennsylvania State University, 2012.
[20] ATKINS B, HENDERSON T. Under-actuated moving mass attitude control for a 3U CuBeSat mission[C]//Proceedings of Spaceflight mechanics 2012. Charleston: American Astronautical Society, 2012: 2083-2094.
[21] KEVIN L Z, JERRY F, DARREN R, et al. CubeSat solid rocket motor propulsion systems providing delta-Vs greater than 500 m/s[C]//Proceedings of 28th Annual AIAA/USU Small Satellite Conference. Utah: Utah State University, 2014.
[22] 屠善澄. 卫星姿态动力学与控制(1)[M]. 北京: 中国宇航出版社, 1999: 49-73.
TU S C. Satellite attitude dynamic and control(1)[M]. Beijing: China Astronautic Publishing House, 1999: 49-73 (in Chinese).
[23] 张晓宇, 贺有智, 王子才. 基于H∞性能指标的质量矩拦截弹鲁棒控制[J]. 航空学报, 2007, 28(3): 635-640.
ZHANG X Y, HE Y Z, WANG Z C. Robust control of mass moment interception missile based onH∞performance characteristics[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(3): 635-640 (in Chinese).
(责任编辑: 张玉, 李世秋)
Design of moving-mass attitude control system for nanosatellites inorbital transfer stage
LUZhengliang,ZHANGXiang*,YUYongjun,MOQiankun,LIAOWenhe
CollegeofMechanicalEngineering,NanjingUniversityofScienceandTechnology,Nanjing210094,China
A moving-mass control technology is proposed to stabilize the attitude of nanosatellites in orbital transfer stage. After the configuration of actuator masses is obtained, 8 DOF dynamic equations are derived based on momentum and moment of momentum theorem. According to the results of dynamic analysis, a simplified control model is developed. On this basis, a robust controller characterized by a global sliding mode is given to stabilize the yaw and pitch angle and to track the actuator position. The validation of this control system is simulated with the condition of parametric uncertainty. Results indicate that the two-dimensional mass moment control system could rapidly adjust the attitude and have a good robustness against disturbance. It is concluded that this system can be applied for attitude control in orbital transfer.
orbital transfer; nanosatellite; moving-mass; attitude control; sliding mode control
2016-09-12;Revised2016-10-11;Accepted2016-11-21;Publishedonline2016-11-280922
URL:www.cnki.net/kcms/detail/11.1929.V.20161128.0922.004.html
TheScientificResearchProjectofNJUST(30916011101)
2016-09-12;退修日期2016-10-11;录用日期2016-11-21; < class="emphasis_bold">网络出版时间
时间:2016-11-280922
www.cnki.net/kcms/detail/11.1929.V.20161128.0922.004.html
南京理工大学自主科研专项 (30916011101)
*
.E-mailzhxiang2002@126.com
陆正亮, 张翔, 于永军, 等. 纳卫星变轨段质量矩姿态控制系统设计J. 航空学报,2017,38(6):320778.LUZL,ZHANGX,YUYJ,etal.Designofmoving-massattitudecontrolsystemfornanosatellitesinorbitaltransferstageJ.ActaAeronauticaetAstronauticaSinica,2017,38(6):320778.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2016.0306
V448.222
A
1000-6893(2017)06-320778-11
*Correspondingauthor.E-mailzhxiang2002@126.com

