泵送混凝土对铝合金模板的冲击
魏德敏+黄佩雯
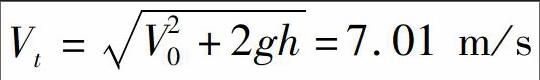

摘要: 对铝合金模板在泵送混凝土浇筑过程中的非线性冲击响应进行有限元分析,考虑泵送混凝土的黏度和密度、泵送管道的直径、模板的宽度和边界条件、混凝土浇筑位置和初始冲击速度等不同因素的影响。研究结果表明:浇筑过程中泵送混凝土的初始冲击速度对模板的冲击响应影响最大,混凝土黏度的影响较小;提高混凝土的泵送速度、增大泵送管道的管径和模板宽度,模板的冲击响应随之增大;模板边界约束越弱其位移响应越大,但其最大等效应力和最大塑性应变越小。
关键词: 铝合金模板; 泵送混凝土; 非线性动力响应; 浇筑速度
中图分类号: TU755.21 文献标志码: B
Impact of pumped concrete on aluminum alloy formwork
WEI Demina,b, HUANG Peiwena
(a. School of Civil Engineering and Transportation; b. State Key Laboratory of Subtropics Architecture Science,
South China University of Technology, Guangzhou 510640, China)
Abstract: The nonlinear dynamic response of aluminum alloy formwork during the pouring of the pumping concrete is analyzed using finite element method. Different parameters are considered, such as the viscosity and density of the pumping concrete, the diameter of pumping pipe, the boundary condition and the width of the formwork, the casting position and initial impact velocity of the pumping concrete. The study results show that the greatest influence on the impact response is the initial impact velocity of the pumping concrete, while the influence of concrete viscosity is little; the impact response on formwork increases with the increase of the pumping velocity and the diameter of pump pipe and the width of the formwork; while the boundary constraint is reduced, the displacement response increases, but the maximum equivalent stress and the maximum plastic strain decrease.
Key words: aluminum alloy formwork; pumping concrete; nonlinear dynamic response; pouring velocity
0 引 言
隨着建筑技术的发展,新型铝合金模板在混凝土浇筑工程中不断推广应用,并逐渐取代传统木模板、钢模板和竹胶合模板。铝合金模板的投入使用仅有十几年,所以目前关于铝合金模板的研究成果很少,且主要是静力试验研究和理论分析。[1-2]在混凝土浇筑过程中,质量不断变化的液态混凝土集中冲击铝合金模板,引起模板的非线性动力响应和永久变形,使模板的重复使用率降低。因此,铝合金模板的动力安全性存在一些亟待解决的问题。但是,关于铝合金模板抗冲击性能的研究成果尚未见报道,其他结构的相关研究也相对较少。
梁超等[3]研究液滴撞击不同浸润性壁面的动态过程。卢西伟[4]通过三维模型试验,研究波浪对船舶运动及撞击能量的影响。刘富等[5]采用光滑粒子动力学SPH方法,对飞机油箱在箱内液体晃动时的动力响应进行数值分析,研究油箱内液体晃动对结构安全性的影响。VIGNJEVIC等[6]分析直升飞机底部金属结构板垂直撞击水面时的动力响应,考虑多种因素的影响。谢永慧等[7]将光滑粒子流体动力学与有限元耦合运用于高速液体冲击下有机玻璃和钢材表面的损伤分析。
本文采用通用有限元分析软件,对常用的铝合金楼面模板在浇筑混凝土过程中的非线性动力响应进行计算,分析对比不同因素的影响,得到模板的抗冲击性能及其主要影响因素。
1 计算模型
常用铝合金模板的长度为1 100 mm,宽度b=200~400 mm,面板的厚度为4 mm;其边肋及端肋厚度为5 mm,高度为65 mm;用2道加筋肋将模板分成三跨,见图1。
建立泵送混凝土冲击铝合金模板的有限元分析模型,见图2。铝合金模板采用S4R壳体单元,沿模板厚度方向均匀设置5个积分点。模板上方的混凝土采用EC3D8R欧拉单元。图中柱状区域为泵送混凝土的流动区域,其上表面为混凝土流入面,采用自由流入的欧拉边界条件,当一部分混凝土流出该柱状区域后另一部分混凝土将通过该表面自由流入,以此描述混凝土不断浇筑于模板的动态过程,且假设混凝土可以流出该块模板。泵送混凝土与模板的动态接触过程采用通用接触模拟,主要考虑泵送混凝土的黏度系数和密度、泵送管道的直径、铝合金模板的边界条件和宽度、混凝土的浇筑位置和初始冲击速度等因素对模板非线性冲击响应的影响。endprint
2 影响参数分析
铝合金材料采用不考虑温度效应的J-C本构关系,即
式中:σ为等效应力;εp为有效塑性应变;ε·*为有效塑性应变εp与参考塑性应变率ε·0之比;A为材料的屈服应力;B为幂指前系数;C为应变率敏感因数;n为硬化因数。采用文献[8]的试验结果:A=205.78 MPa,B=130.59 MPa,C=0.015,n=0.357。
2.1 混凝土黏度
不同标号泵送混凝土黏度系数的变化范围分别为:C25,η=1.12~2.32 Pa·s;C30,η=1.63~2.56 Pa·s;C35,η=1.75~2.95 Pa·s。[9]混凝土的密度ρ=2 000~3 200 kg/m3。首先分析混凝土黏度系数η=2.0 Pa·s,ρ=2 400 kg/m3,泵送管道直径d=150 mm,混凝土浇筑速度Vt=7.0 m/s,浇筑位置为模板的中心,模板的边界条件为端肋简支边肋自由,模板宽度b=400 mm的铝合金模板的冲击响应,然后分析其他基本参数不变,黏度系数变化的情况。
在300 ms浇筑时间内,当混凝土垂直冲击模板中心时,铝合金模板产生最大变形时刻(t=3.60 ms)的变形云图和横纵截面挠度曲线见图3,其中Umax为最大挠度。由此可知,泵送混凝土垂直浇筑在模板中心时,模板中心处产生明显的向下凹陷,模板变形集中在模板的中跨,边跨变形很小。横纵截面的挠度曲线均为关于中点对称的下凹抛物线,最大挠度发生在浇筑处。
模板中心的挠度时程曲线见图4,挠度向下为正。由此可以看出,当泵送混凝土垂直浇筑在模板中心处时,模板中心挠度在极短的时间内从0增大至最大值Umax≈9.500 mm,在200 ms时间内中心挠度波动的幅值逐渐减小,最后趋于稳定,挠度平均值随时间的增加而增大。混凝土黏性系数变化时模板冲击响应计算结果见表1,其中Ur为最终挠度,σmax和εp,max分别为模板的最大等效应力和最大有效塑性应变,TU和Tσ分别为Umax和σmax出现的时间,Aε为塑性变形区的面积。
由表1可知,模板最大挠度、最终挠度、最大等效应力和最大有效塑性应变值随黏度系数的提高而增大,而最大挠度和最大等效应力出现的时间及塑性变形区的面积基本相同。泵送混凝土的黏度系数增大至3倍时,模板最大挠度、最终挠度、最大等效应力和最大有效塑性应变的值分别增大到1.001,1.011,1.003和1.080倍。显然,混凝土黏度系数对模板冲击响应的影响较小。
泵送混凝土黏度系数η=2.0 Pa·s时模板的最大等效应力云图和最终塑性变形云图见图5和6。
由图5可知,模板的最大等效应力出现在模板中心,应力云图为中心对称的椭圆形,模板边跨的等效应力值较小。由图6可知,塑性变形仅发生在模板中心区域,其余区域处于弹性变形状态。
2.2 混凝土密度
混凝土根据密度可分为重混凝土、普通混凝土和轻质混凝土[10],ρ<2 000 kg/m3为轻质混凝土,ρ=2 000~2 800 kg/m3为普通混凝土,ρ>2 800 kg/m3为重混凝土。
分析在其他基本参数不变的情况下,浇筑不同密度的混凝土对铝合金模板冲击响应的计算结果见表2。
由此可以看出,ρ在2 000~3 200 kg/m3范围内变化时,模板最大挠度、最大等效应力和最大塑性应变出现的时间大致相同。这些最大响应值均随着混凝土密度的提高而增大。当ρ增大1.6倍时,模板的最大挠度、最终挠度、最大等效应力和最大塑性应变值分别增大1.270,1.393,1.056和6.542倍,而模板中心塑性变形区的面积增大8.0倍。显然,混凝土密度对模板的塑性变形影响较大。
2.3 混凝土泵送管管径
为保证混凝土在泵送管道内能自由流动不致堵塞,目前国内混凝土泵送管道直径d一般为100~175 mm,最常用的是150和175 mm这2种管径。[11]当η=2.0 Pa·s,ρ=2 400 kg/m3,Vt=7.0 m/s,泵送混凝土垂直撞击端肋简支、边肋自由的铝合金模板中心时,d变化对模板冲击响应的影响见表3。
由表3可知:d越大,模板的最大挠度值越大且出现时间越晚,最大等效应力值也越大且其出现时间基本不变。当d从100 mm增大至175 mm时,模板的最大挠度、最终挠度及最大等效应力值分别增加到2.280,1.860和1.480倍。d不超过125 mm时,模板响应为弹性的;d为150 mm和 175 mm时,模板中心出现圆形塑性变形区,该塑性变形区的面积及其最大塑性应变值随管径的增大而增大。可见,泵送管径对模板的位移和塑性变形影响较大。
2.4 约束条件
模板约束条件一般分为3类:端肋、边肋均简支(Ⅰ类),端肋简支、边肋横向约束(Ⅱ类),端肋简支边肋自由(Ⅲ类),见图7。取η=2.0 Pa·s,ρ=2 400 kg/m3,d=150 mm,Vt=7.0 m/s,b=400 mm,这3类约束模板中心受混凝土垂直撞击时的非线性动力响应见表4。由表4可以看出:I类和II类约束模板的最大挠度和最大等效应力出现的时间要比Ⅲ类早;Ⅰ类约束模板的最大挠度和最终挠度最小,Ⅱ类约束略有增大,Ⅲ类约束模板的最大挠度和最终挠度分别为Ⅰ类的1.133和1.483倍;Ⅲ类约束模板的最大等效应力、最大塑性应变和塑性变形区面积最小,Ⅱ类次之,Ⅰ类最大且分别为Ⅲ类的1.032,2.886和8.000倍。可见,模板边界约束越弱,泵送混凝土撞击引起的位移响应越大,等效应力和塑性应变响应越小,塑性变形区越集中。
2.5 澆筑位置
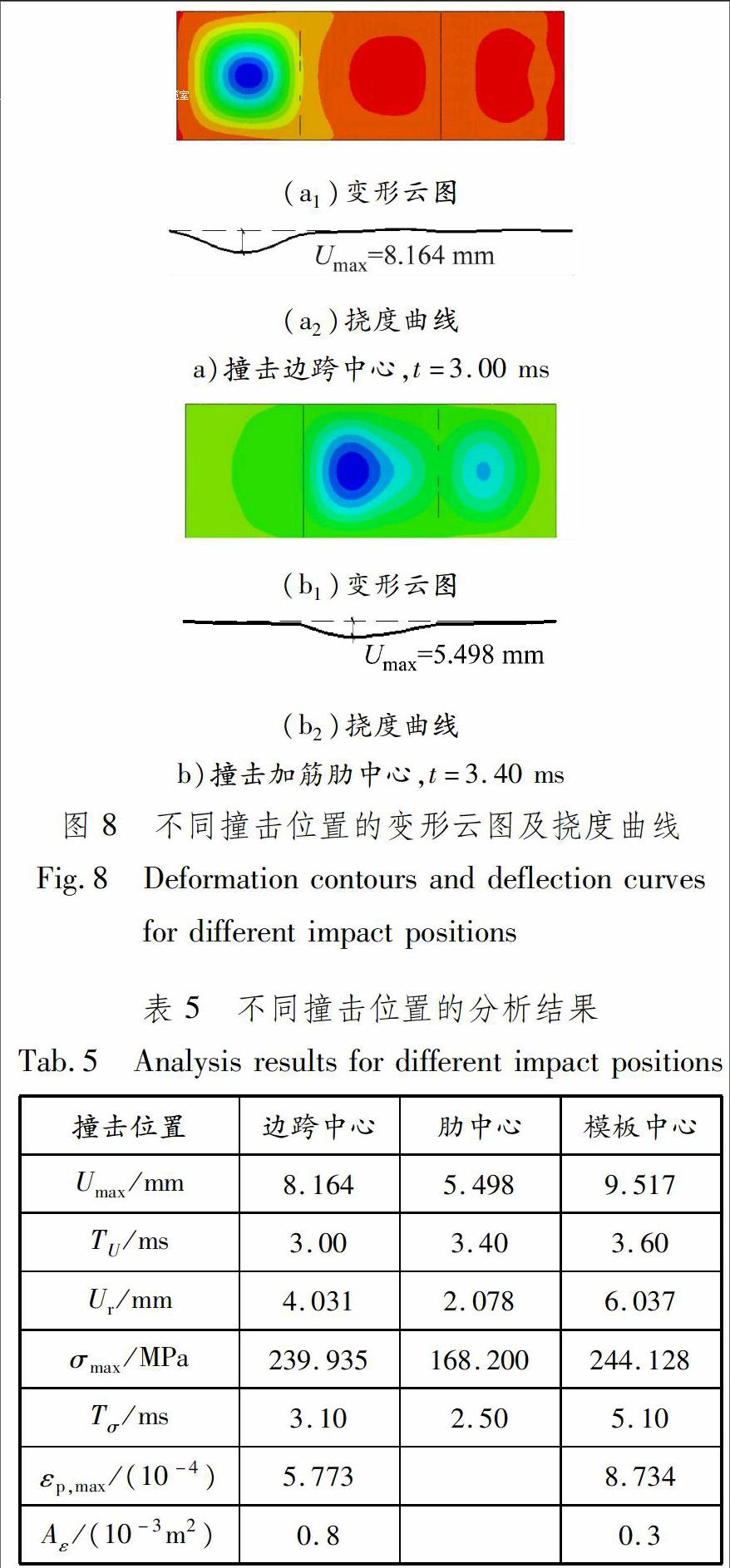
混凝土浇筑在模板上的位置不同,对模板的冲击也不同。本文考虑3种浇筑位置:边跨中心、加筋肋中心和模板中心,其他基本参数不变。泵送混凝土浇筑在模板不同位置时,模板的最大变形云图和横纵截面挠度曲线见图8,部分响应计算结果见表5。对比图8和图3可知:当泵送混凝土撞击模板边跨中心和模板中心时模板的最大变形出现在浇筑处,最大变形显示为以浇筑点为中心的圆向外逐渐扩展为矩形,变形区域集中在受撞击的跨;当泵送混凝土撞击加筋肋中心处时,由于加筋肋的约束作用,最大挠度出现在靠近受撞击点的模板中跨,最大变形云图也不同于另外2种情况。由表5可知:模板的最大挠度出现时间为混凝土浇筑在模板边跨中心时最早、浇筑在模板中心时最晚;最大挠度值出现时间为浇筑在加筋肋中心时最小、浇筑在模板中心时最大且为浇筑在加筋肋中心的1.731倍;模板最大等效应力出现的时间是浇筑在加筋肋中心时最早且数值最小,浇筑在模板中心时最大等效应力出现的时间最晚且数值最大,为浇筑在加筋肋中心时的1.451倍。当泵送混凝土浇筑在加筋肋中心时,模板处于弹性变形状态,而浇筑在边跨和模板中心时模板将发生塑性变形,塑性变形是以浇筑点为中心的圆形区域;浇筑在边跨中心的塑性变形区面积为浇筑在模板中心时的2.667倍。endprint
2.6 模板宽度
常用的铝合金楼面模板宽度b分别为200,250,300,350和400 mm,分析其他参数不变,模板宽度变化情况下的非线性冲击响应,结果见表6。由表6可知,当模板的宽度从200 mm增大至400 mm时,模板的最大挠度、最终挠度、最大等效应力和最大塑性应变分别增大到1.440,2.748,1.020和1.596倍,但模板中心处的圆形塑性变形区面积基本不变。可见,模板宽度的增大,对其中心处的最终挠度值影响较大。
2.7 浇筑速度
常用混凝土罐车的最大泵送量Qmax为160~200 m3/h。为避免发生离析现象,混凝土的落料高度不能超过2 m。[12]当d=150 mm,Qmax=200 m3/h时,泵送混凝土在出料口的最大下落速度为V0=3.14 m/s。若出料口与模板的垂直距离为h,则泵送混凝土到达模板表面时的最大浇筑速度为
考虑到混凝土中会含有气体而使输送管的有效截面有所折减或者其他施工中不可控因素的影响,泵送混凝土到达模板表面的最大浇筑速度有可能超过以上计算结果。[13]为此,分析在其他参数不变的情况下,Vt在5.0~13.0 m/s范围变化时模板的非线性动力响应,计算结果见表7。由此可知,当Vt提高时,模板的最大挠度、最终挠度、最大等效应力、最大塑性应变以及塑性变形区域面积将增大,而最大挠度与最大等效应力出现的时间有所提前。当Vt达到13.0 m/s时,模板的最大挠度、最终挠度和最大等效应力分别为Vt=5.0 m/s时的2.019,2.630和1.307倍。当Vt=5.0 m/s时,模板未出现塑性变形。当Vt由7.0 m/s增长到13.0 m/s时,最大塑性应变和塑性变形区域面积分别增大5.70和20.33倍。显然,混凝土浇筑速度对模板的非线性响应影响较大。
混凝土浇筑速度与模板最大等效应力和最大塑性应变的关系分别见图9和10。
由图9可知:模板最大等效应力随混凝土浇筑速度的提高而增大;当Vt<7.0 m/s时最大等效应力的增长率较大;当Vt≥7.0 m/s时增长率基本不变,逐渐趋于稳定值250 MPa。由图10可以看出,当Vt≥11.0 m/s,最大塑性应变随浇筑速度增长的幅度明显增大。
3 结 论
对泵送混凝土浇筑铝合金模板的动态响应过程进行非线性有限元计算和参数分析,得到以下主要结论。(1)泵送混凝土的黏度对铝合金模板的冲击响应的影响不大,黏度系数增大,模板的最大响应值略有增大。(2)泵送混凝土密度和泵送管道直径增大时,模板的最大响应值增大。(3)模板边界约束越弱、宽度越大,模板的刚度越小,浇筑混凝土引起的模板位移响应越大,而等效应力响应越小。(4)混凝土浇筑位置在加筋肋中心时,模板的动力响应最小,且为弹性响应。(5)泵送混凝土的浇筑速度对模板动力响应的影响较为明显。当浇筑速度大于7.0 m/s时,模板将出现塑性变形,因此使用铝合金模板的工程中混凝土的最大浇筑速度应小于7.0 m/s。
参考文献:
[1] 黎方文. 新型铝合金模板试验测试[J]. 施工技术, 2013, 42(S1): 279-280.
LI F W. Test to new style alloy aluminum formwork[J]. Construction Technology, 2013, 42(S1): 279-280 .
[2] 孙思为. 基于有限元方法的铝合金模板受力分析[J]. 山西建筑, 2014, 40(14): 61-62.
SUN S W. Force analysis on alloy aluminum formwork based on FEM method[J]. Shanxi Architecture, 2014, 40(14): 61-62.
[3] 梁超, 王宏, 朱恂, 等. 液滴撞击不同浸润性壁面动态过程的数值模拟[J]. 化工学报, 2012, 64(8): 2745-2751.
LIANG C, WANG H, ZHU X, et al. Numerical simulation of droplet impact on surfaces with different wettabilities[J]. CIESC Journal, 2012, 64(8): 2745-2751.
[4] 卢西伟. 开敞水域系泊船舶运动及动力响应研究与泊位优化[D]. 大连: 大连理工大学, 2009.
[5] 刘富, 童明波, 陈建平. 基于SPH方法的三维液体晃动数值模拟[J]. 南京航空航天大学学报, 2010, 42(1): 122-126.
LIU F, TONG M B, CHEN J P. Numerical simulation of three-dimensional liquid sloshing based on SPH method[J]. Journal of Nanjing University of Aeronautics & Astronautics. 2010, 42(1): 122-126 .
[6] VIGNJEVIC R, MEO M. Simulation of helicopter under-floor structure impact on water[J]. International Journal of Crashworthiness, 2001(3): 425-443. DOI: 10.1533/cras.2001.0188.
[7] 谢永慧, 汪勇, 陈建辉, 等. 固体材料在高速液体撞击下的表面损伤研究[J]. 兵工学报, 2009, 30(2): 139-144.
XIE Y H, WANG Y , CHEN J H, et al. Research on surface damage of solid material subjected to high speed liquid impact[J]. Acta Armamentarh, 2009, 30(2): 139-144.
[8] 刘再德, 王冠, 冯银成, 等. 6061铝合金高应变速率本构参数研究[J]. 矿冶工程, 2011, 31(6): 120-123
LIU Z D, WANG G, FENG Y C, et al. High-strain-rate constitutive parameters of 6061 aluminum alloys[J]. Mining and Metallurgical Engineering, 2011, 31(6): 120-123 .
[9] 钟一鸣. 不同类型减水剂配制混凝土的流动与其砂浆流变参数的关系[D]. 广州: 华南理工大学, 2012.
[10] 李沙, 李作浩, 许辅瑶, 等. 浅析混凝土泵送输送管道的选型和布置[J]. 工程机械, 2011, 42(10): 40-43
LI S, LI Z H, XU F Y, et al. Analysis on the type selection and arrangement of concrete pump transmission pipeline[J]. Construction Machinery and Equipment, 2011, 42(10): 40-43.
[11] 混凝土質量控制标准: GB 50164—2011[S].
[12] 蒋临亭. 泵送混凝土对水平模板的冲击荷载计算[J]. 建筑技术, 1986, 17(S1): 31-32.
JIANG L T. Impact load calculation of pumping concrete for horizontal formwork[J]. Architecture Technology, 1986, 17(S1): 31-32.endprint

