机动车加油管注油过程的Workbench Fluent仿真

程秀，莫健华，明志新，刘祖强

（1.华中科技大学 材料科学与工程学院，湖北 武汉 432700；2.湖北水利水电职业技术学院 机电工程系，湖北 武汉 432700）

机动车加油管注油过程的Workbench Fluent仿真

程秀1,2，莫健华1，明志新2，刘祖强2

（1.华中科技大学 材料科学与工程学院，湖北 武汉 432700；2.湖北水利水电职业技术学院 机电工程系，湖北 武汉 432700）

随着环保要求的日益严格，机动车加油过程所产生的油气排放污染控制越来越严格. 针对此问题，选择一体化软件Workbench 对简化后的油管模型进行网格划分，再使用VOF多相流模型和RNGk-ε模型对油管的注油过程进行模拟计算. 设置好边界条件以及求解条件，建立仿真模型，对不同内径加油管在不同加油速度下的注油过程进行两相流模拟计算，讨论其对液封形成的影响. 结果表明，加油速度越大，加油管径越小，自液封越容易形成，但是速度大、管径小容易导致反喷.

加油排放；计算流体力学；数值模拟；油管液封

在加油过程中，汽油蒸发的排放占整个机动车油气排放的20%，造成大量能源的损失和大气的污染，因此必须重视[1-6]. 车载油气回收系统（On-board Refueling Vapor Recovery，ORVR）在美国首先提出来，系统要求在加油管某处完全充满汽油以形成自液封，使油气不向大气中排放而只能被液态汽油带入油箱内，以减少机动车加油过程中油气的排放[2,7].

机动车注油过程瞬间万变，有三维的瞬态流动、气液相变流动，还有自由表面紊流等. 计算流体力学CFD的快速发展，使得仿真机动车加油过程变得简单可行. 美国的Stoneman教授[8]和加拿大温莎大学[9]都利用CFD对加油管的加油过程进行了模拟仿真，取得了显著的成果，但是受限于早期计算机的水平，模拟结果跟实际加油过程有一定的差距，而且相关研究结果多是二维模拟. 中国在2008年才有人开展这方面的工作，国内做得较好的是江苏大学的何仁教授课题组以及北京石油化工学院的陈家庆教授课题组. 他们采用CFD数值模拟对机动车加油过程中气液两相流动特性进行了分析，但他们使用的网格划分软件和仿真计算软件是独立的，从而影响了计算精度[2,10]. 本研究借助网格划分和仿真计算一体化的软件Workbench Fluent，对不同内径加油管在不同加油速度情况下的液封性能进行数值模拟，分析研究了加油管内径和加油速度对液封性能的影响.

1 模型介绍

1.1 加油管的几何模型

某型号的汽车加油管的几何模型如图1所示，4个拐角的存在有利于液封的形成. CFD数值模拟使用的模型在保证主要结构特征的前提下需尽量简化并转化成包裹的实体，对图1的加油管进行简化得到图2所示的简化模型，保留4个拐角几何结构特征不变. 加油枪的喷嘴直径是标准的，需要与加油管的管口相配套，根据市场使用情况选择直径为20 mm的喷嘴. 加油管的直径选择33 mm和25 mm两种.

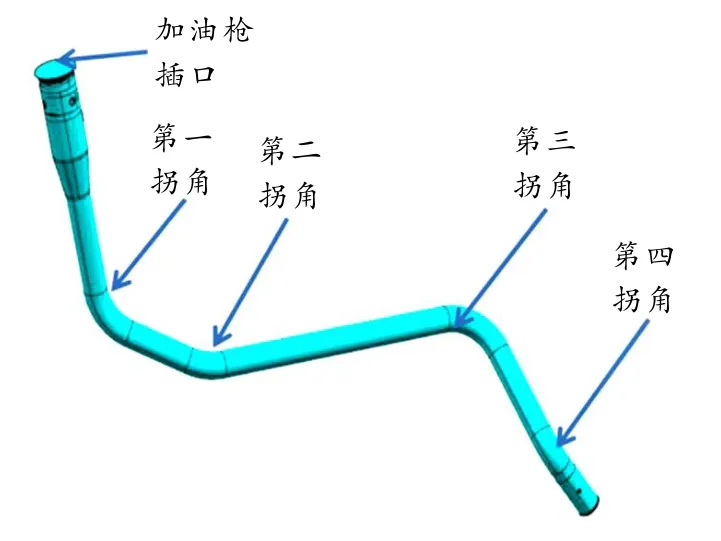
图1 加油管的几何模型

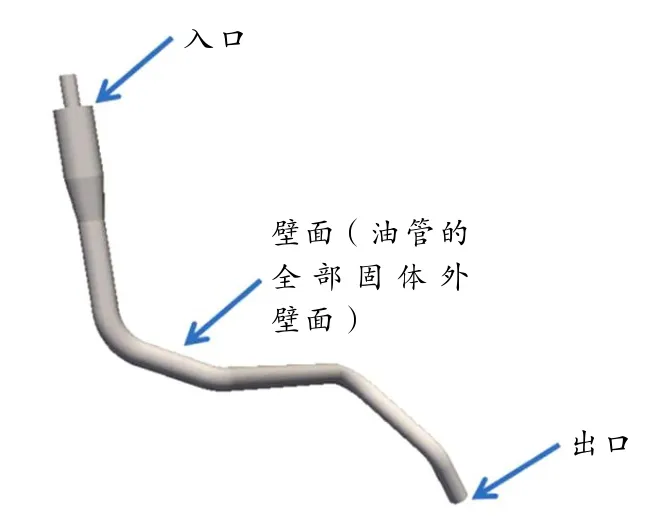
图2 简化的加油管几何模型

1.2 网格划分和相关设置

采用Workbench Fluent 自带的划分网格软件对加油管模型进行网格划分. 为减少计算时间和工作量只计算加油管部分，全部采用六面体网格以保证精度. 网格如图3所示，不管是截面（图3-a）还是表面（图3-b)，网格规整，无明显变形区域，说明网格划分合理.

图3 油管网格模型

边界条件设置：加油枪嘴的油出口设为速度入口（Velocity Inlet），加油管末端设为压力出口（Pressure Outlet）；加油管的全部固体外壁面和加油枪喷嘴段的外壁作壁面(Wall) 处理. 速度入口处液态汽油的体积百分比设为1，湍流强度都取为5% ，水力直径取各自的管道直径.

空气和汽油为计算材料. 空气的密度为1.225 kg/m3，粘度为1.789 4×10-5kg· m-1·s-1；汽油的密度为720 kg/m3，粘度为5.4×10-4kg· m-1·s-1.

1.3 数学模型

汽油从加油管入口注入油管，并沿着加注管流向第一个拐角处，在重力及惯性作用下顺流而下，依次流过第二至第四拐角，最后注入油箱. 加油过程复杂多变，涉及到非稳态、多相流、湍流等众多因素，不可能考虑所有的因素[11]. 因此假设：等温条件下加油，气液两相之间无热传递、传质现象，忽略浮力[2,7].力，从而导致压力梯度.

1.3.1 多相流模型选择

Workbench将求解器看作一个组件，Fluent是其中的一个，它包括一系列的多相流模型，我们采用VOF（Volume of Fluid）多相流模型. 加油过程是气液两相湍流流动，VOF模型能够准确计算层流、液体中有大气泡流动、水坝决堤的水流等复杂情况下流体的动态特性，并能精确液-气分界面的稳态或瞬时分界面[12-13].

在VOF 模型中，气相和液相可以看成是两种互不相溶、不可压缩的流体，其平均质量守恒方程和平均动量守恒方程[2,7]：

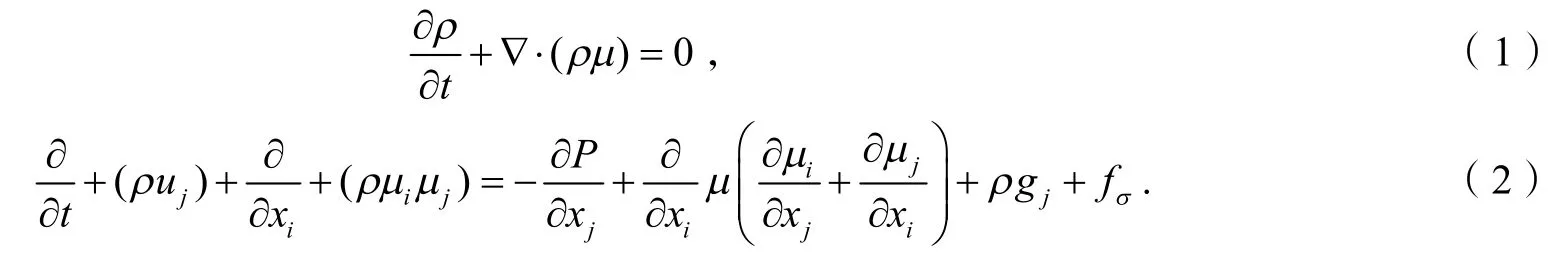
式中，ρ为密度，kg/m3；t为时间，s；x,u为速度矢量，m/s；P为压力，Pa；μ为动力学粘度，Pa· s；g为重力加速度，kg· m· s-1；fσ表面张力引起的体积力，N；i,j为坐标.

混合物的密度和动力粘度可以通过平均体积分数的方法来求[2]：

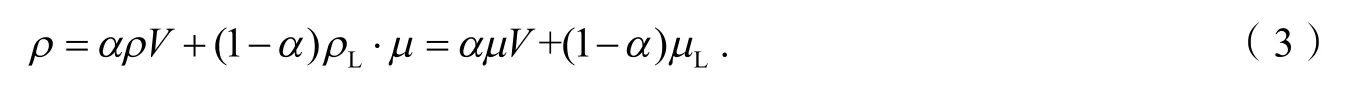
式中，α为体积分数.

气液两相之间的界面会产生不同的表面张力，而且是突变，如图4所示. 假设液滴是一个球，半径为r，球缺底半径为1r.A、B点水平方向合力相互抵消，竖直方向的合力为必将产生一个附加压

图4 气液界面模型

因此，压力梯度必须与动量方程中额外的体积力相等以维持平衡. 给气液一个一定厚度的过渡区，该不连续的压力突变可以表示为[2,7]：

式中，σ为表面张力，N.

那么在连续域内的气体体积分数则由体积分数的连续方程求解[2,7]：

气液两相界面处计算单元为0＜α＜1.

1.3.2 湍流模型的选择

湍流模型对计算精度有显著影响，因此必须选择合适的湍流模型. Workbench Fluent求解器中提供的湍流模型包括标准k-ε模型以及其变型RNGk-ε模型、雷诺应力模型（Reynolds Stress Model，RSM）和大涡模拟（Large Eddy Simulation，LES）等. 加油管因为加油速度快呈现出强湍流状态，并且拐角是急弯度，因此选择RNGk-ε模型，其动能方程和能量耗散方程分别如下[2,7,14]：

式中，k为湍动能，m2/s2；Gk为平均速度梯度产生的湍动能，m2/s2；Gb为浮力产生的湍动能，m2/s2；ε为湍流耗散率；常量

2 仿真计算结果与分析

加油时汽油首先以一定的速度从加油枪管口喷射而出，在重力及速度惯性的作用下沿着油管向下流动，在加油管喉管处汽油与通风管处的汽油蒸气混合，并伴随空气的卷吸与汽油的相变，在拐角处发生碰撞冲击，最终进入油箱. 气液两相混合物在重力及速度惯性的作用下流入燃油箱中.

加油管的几何结构对加油过程有影响，但加油管机械结构受制于车身，所以主要通过规范加油速度以及加油管的内径来实现自液封和抑制反喷. 文献[7]提到：加油速度过小，填充时间长，空气有充分的时间卷入，液封不易形成；加油速度过大，又增加提前跳枪停止加油的可能性. 国标中规定加油速度不能超过4.5 m/s，本研究选择2～3 m/s. 已有的计算结果表明，汽油充满整个油管的时间小于2 s.

2.1 加油管径为33 mm的计算结果

实际加油过程中油管的流体力学特性与加油速度直接相关. 33 mm的管径相对来说比较大，为此，选取加油速度为2 m/s、3 m/s. 加油管油帽段上部有一管口连通大气，使出口压力相对于大气压为0. 图5是油管直径为33 mm，两种不同速度下第一拐角横截面汽油占比云图（红色的代表汽油，蓝色代表气体）. 通过对比颜色，估算出汽油体积占比. 从图5可以看出：速度为2 m/s的汽油体积占比约为80%，速度为3 m/s的汽油体积占比约为75%. 由于自重以及油从加油枪快速冲出，在第一拐角处发生激烈碰撞并产生旋流，使得湍流现象更加复杂，汽油在加油管中在第一拐角处出现的喷溅、碰撞、旋流等现象符合流体动力学的规律，与机动车加油过程的特性吻合.

图5 d=33 mm ，不同速度下第一拐角油气体积分数截面图

图6是两种加油速度下第一拐角处的速度云图. 截面的节点数是一个定值，速度是矢量，从图中可以看出有部分液体的速度因为碰撞发生反弹，出现与宏观速度方向相反的矢量. 粗略估算图6-a的反向矢量个数小于图6-b反向矢量的个数，图6-b中的拐角速度矢量变向明显增多，这说明速度大，碰撞的几率增大. 反向矢量多，反弹的几率大，这必将增大发生反喷的几率，从而造成提前“跳枪”.因此，必须严格控制加油枪的最大加油流量，不能一味追求快速，否则欲速则不达.

图6 d=33 mm ，不同速度下第一拐角的速度云图

图7是汽油体积分数云图，为了对比明显，以蓝色显示体积分数大于50%的气体体积，完全断开的空白区域视为汽油形成的液封. 由图7可知：两种速度都可以形成液封，但是速度大者加油管中的汽油体积率也大，形成液封的时间短、长度大，液封效果好. 整个油管充满油的时间小于2 s，比较短. 因此本文没有探讨液封形成需要的时间. 4个拐角的存在，使油管的流线复杂，降低了汽油在管内的流速，有利于液封的形成.

图7 d=33 mm ，不同速度下汽油体积分数云图（蓝色代表气体）

2.2 加油管径为25 mm的计算结果

减小油管直径也可以降低汽油在管内的流速. 文献[7]的结果显示：直径为25 mm的自液封效果较好，因此对这种规格的管径也进行仿真计算. 25 mm的管径较小，采用加油速度为2 m/s和2.5 m/s.

图8是管径为25 mm的油管第一拐角处截面汽油体积占比云图. 不同速度的汽油体积占比区分不明显，但是速度大者的截面汽油分布不规则，说明冲击搅拌现象剧烈. 由于汽油在第一拐角经过垂直加速后突然改变方向，在第二拐角产生强烈的能量耗散，速度迅速减小，冲击力减小，有利于液封的形成. 但是管径过小，加油速度不变，会导致在拐角处的剧烈冲击碰撞，产生汽油回溅.

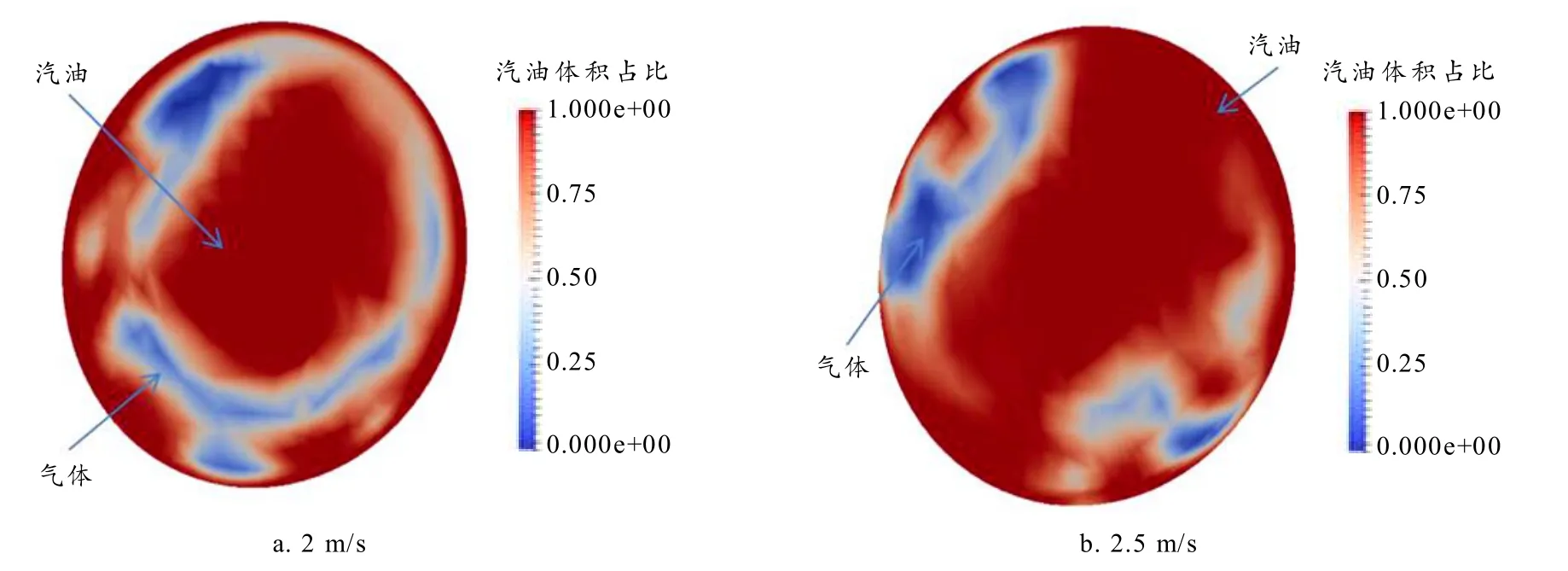
图8 d=25 mm ，不同速度下第一拐角油气体积分数截面图

从图9中可以估算出两种速度下反向矢量占比比较接近. 汽油从加油枪管口喷射流出，碰到加油管壁面后一部分碰撞反弹，一部分沿管壁下流. 管内汽油呈强湍流流动状态，伴随有碰撞、旋流等现象，速度大者，这个现象更加明显，速度反向矢量显著增加，但是在数据统计的时候因为统计方法的误差，该差别不是很明显.

图9 d=25 mm ，不同速度下第一拐角的速度云图

如图10所示，油管直径25 mm的加油管中第一拐角与第二拐角之间形成大段的液封区域，但是速度大者液封长度明显大于速度小者的. 这符合文献[7]所述. 注油过程与管径为33 mm管径的注油过程类似，不同之处在于湍流、碰撞、旋流程度不同而已. 要区分速度对注油过程的影响，还需要进一步的仿真计算. 液封形成原理及过程与前述相同.

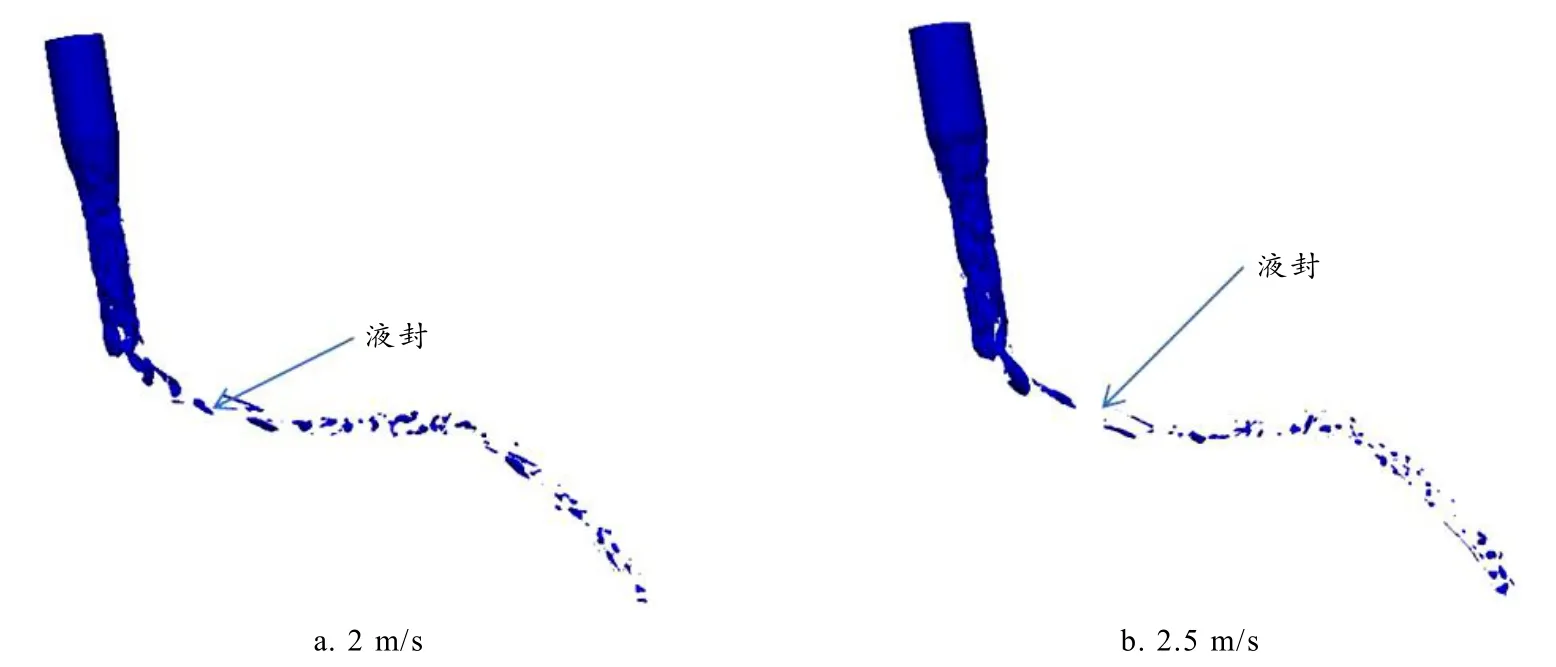
图10 d=25 mm ，不同速度下汽油体积分数云图（蓝色代表气体）

由图7和图10可知：自液封主要发生在第一至第二拐角的水平段，空白长度越大，液封长度越大，自液封效果越好；管径相同，速度大者液封长度大；加油速度相同，管径小者液封效果稍好. 这个结果与文献[7]的结果相符，同时说明本文研究模型可靠.

3 结论

利用Workbench Fluent对两种直径的加油管在不同加油速度的流体力学特性进行仿真计算，得到以下结论：

1）保持加油管的4个拐角几何特征不变，增大加油速度和减小加油管直径，有利于自液封的形成，但反喷倾向增大，会增加提前“跳枪”的可能性.

2）综合考虑自液封和反喷的情况，相对较好的加油参数是加油管径25 mm、加油速度2.5 m/s.

3）Workbench Fluent通过合理边界条件的设置，可以对复杂的加油过程进行有效的计算模拟，从而预测加油过程容易出现的问题，在实际中加以改进，可以有效缩短研发周期、降低成本.

本研究由于时间等方面的影响，考虑的参数不多，因此统计数据存在误差，几个结论只是定性结论. 因此在今后的工作中需要增加加油速度、管径参数以及油管几何结构的考虑，以减少统计数据的误差.

[1] LIU Huan, MAN Hanyang, TSCHANTZ M, et al. VOC from vehicular evaporation emissions∶ status and control strategy [J]. Environmental Science & Technology, 2015, 49(24)∶ 14424-14431.

[2] 汪智，何仁. 基于Fluent仿真的ORVR加油管液封设计[J]. 重庆理工大学学报（自然科学版），2014, 28(2)∶16-21.

[3] YAMADA H, SATOSHI I, HIROSHI T. Refueling emissions from cars in Japan∶ compositions, temperature dependence and effect of vapor liquefied collection system [J]. International Journal of Social Economics, 2015,36(5)∶ 658-678.

[4] YANG Xiaofan，LIU Huan, CUI Hongyang, et al. Vehicular volatile organic compounds losses due to refueling and diurnal process in China∶ 2010-2050 [J]. Journal of Environmental Sciences, 2015, 33(7)∶ 88-96.

[5] 杜建波，方茂东，陆红雨，等. 加油排放试验程序的设计和车载油气回收系统开发的建议 [J]. 汽车工程，2014, 36(5)∶ 537-541.

[6] 朱玲，陈家庆，王耔凝. 车载加油油气回收ORVR系统应用进展[J]. 油气储运，2015, 34(5)∶ 469-476.

[7] 汤水清，陈家庆，刘美丽，等，ORVR系统加油管液封性能数值模拟[J]. 汽车工程学报，2016, 6(3)∶ 187-195.

[8] STONEMAN S. On the design of automotive fuel filler pipes [J]. Automotive Engineer, 1997, 22(1)∶ 32-36.

[9] ZHAO A G. A hybrid numerical study of automotive fuel tank filling [D]. Canada∶ University of Windsor, 2003.

[10] 陈家庆，张男，王金惠，等. 机动车加油过程中气液两相流动特性的CFD数值模拟[J]. 环境科学，2011,32(12)∶ 3710-3716.

[11] 任碧琪，常耀卿，刘明宇，等. 北京加油站加油速率与车载油气回收系统的兼容性[J]. 环境工程，2015,33(S1)∶ 487-490.

[12] ISSA R I. Solution of the implicitly discretised fluid flow equations by operator-splitting [J]. Journal of Computational Physics, 1986, 62(1)∶ 40-65.

[13] GUEYFFIER D, LI Jie, NADIM A, et al. Volume-of-fluid interface tracking with smoothed surface stress methods for three-dimensional flows [J]. Journal of Computational Physics, 1999, 152(2)∶ 423-456.

[14] YAKHOT V, ORSZAG S A. Renormalization group analysis of turbulence I basic theory [J]. Journal of Scientific Computing, 1986, 1(1)∶ 3-51.

[责任编辑：熊玉涛]

An Oil Injection Process for Motor Vehicle Refueling Based on Workbench Fluent Simulation

CHENG Xiu1,2, MO Jian-hua1, MING Zhi-xin2, LIU Zu-qiang2
(1. School of Materials Science and Engineering, Huazhong University of Science and Technology Wuhan 432700, China; 2. Department of Mechanical and Electrical Engineering, Hubei Water Resource Technical College, Wuhan 432700, China)

With the increasingly stringent environmental requirements, control of pollution from exhaust of oil and gas in motor vehicle fueling process is increasingly stringent. To solve this problem,the integrated software Workbench is selected to generate grid mesh for the simplified tubing model and the VOF model and RNGk-εmodel is applied to simulate and calculate the fuel injection process of oil pipes. The boundary conditions and solution conditions are set and a simulation model is established to simulate and calculate the two-phase flow of the fuel injection process of oil pipes of different sizes at different rates, and its effect on liquid seal is discussed. The results show the greater the fueling rate and the smaller the fuel pipe diameter, the easier it is to form the liquid seal.But the greater rate of fueling and smaller diameter of the tube can easily lead to back spray.

oil and gas emissions from the fueling process; computational fluid dynamics; numerical simulation; filler pipe liquid seal

U473.9

A

1006-7302（2017）04-0032-08

2017-06-13

程秀（1976—），女，湖北广水人，副教授，博士，主要从事计算仿真及机电一体化方面的工作.