基于弯曲高斯过程组合方法的光伏出力预测研究

程泽+刘琦+张霞

摘 要：针对光伏发电功率受多种天气因素影响造成预测难度大的现状，提出了一种基于弯曲高斯过程的混合模型，可以实现一天内任意时刻的光伏出力的概率预测，获得置信区间预测值和点预测值.该算法先由多元自适应回归样条模型实现对多维输入变量的约减，同时得到待预测值的先验数据，然后利用模糊C均值算法按天气类型对训练集数据和测试集的先验数据进行聚类，得到相似样本，再利用弯曲高斯过程模型对测试集数据进行估计，最后利用Bagging算法实现对子混合模型的集成学习，得到待预测值的区间估计和点估计.仿真及试验结果验证了该混合模型的有效性和可靠性.与高斯过程估计和BP神经网络分位数估计相比，该混合模型精度更高，实用性更强.

关键词：多元自适应回归样条；弯曲高斯过程；Bagging算法；区间预测；光伏发电

中图分类号：TM 715 文献标志码：A

A Research of Estimation of Solar Power Generation Based on

Warped Gaussian Process

CHENG Ze1，LIU Qi1，ZHANG Xia2

（1.School of Electrical and Information Engineering，Tianjin University，Tianjin 300072，China；

2.School of Civil Engineering，Qinghai Nationalities University，Xining 810007，China）

Abstract：Considering the situation that photovoltaicpower generation is affected by a variety of weather factors，a hybrid model was proposed based on warped Gaussian process to predict the power generation，where probability of photovoltaic power generation at any time in one day can be realized and prediction point and prediction interval can be obtained. Firstly，multivariate adaptive regression splines model was used to reduce multidimensional input variables，and to obtain the prior data of test. According to the type of weather，fuzzy C-means algorithm was then used to divide the training data and prior data of test，and to obtain the similar samples. The warped Gaussian process was also used to estimate the test data. Finally，bagging algorithm was used to realize the integrated study，and to obtain the prediction interval and prediction point. By the simulation and experimental results，the validity and reliability of this hybrid model was verified. The results show that the hybrid model improves both accuracy and practicability，compared with Gaussian process predictions and BP quantile regression neural network predictions.

Key words：multivariate adaptive regression splines；warped Gaussian process regression； Bagging algorithm； prediction interval；solar power generation

光伏發电在满足能源需求、减少环境污染、改善能源结构等方面发挥着重要的作用，近年来，成为继风力发电之后可再生能源发电的又一增长点，在全球迅速发展.由于日照的昼夜周期性，光伏发电是一种典型的间歇式电源，光伏发电功率受到太阳辐照强度和天气等多种因素的影响，其功率变化具有明显的随机性和波动性，这些特性将使得大规模光伏发电并网对电网造成不良影响.因此对光伏发电功率的准确预测，将对电网调度及电力系统的稳定性和安全性具有重要的意义[1-2].

现今用于短期光伏功率预测的主要算法有人工神经网络算法、分类回归算法、时间序列算法、马尔科夫链算法、小波分析算法等[3-7].虽然不同的算法都有各自的优点，但同时也存在着缺点，因此出现了将不同算法组合起来的综合预测算法.文献[8]提出将多尺度小波分解法与神经网络法组合进行光伏发电预测.文献[9]提出将GMDH神经网络与最小二乘支持向量机相结合进行光伏发电预测.文献[10]提出将PCA算法与最小二乘支持向量机算法组合进行光伏发电预测.文献[11]提出将灰色模型和BP神经网络算法组合进行光伏发电预测.目前，光伏发电预测大多是点预测，即给出某一时刻的一个确定值，但是光伏发电功率具有较大随机性，确定的点预测值很难表达预测结果的不确定，影响电网调度及电力系统的稳定性和安全性.endprint

相比于点预测，概率预测很好地弥补了点预测无法度量预测结果不确定性的缺陷.概率预测方法能给出下一时刻可能的光伏功率值及其置信区间值，提供较全面的预测信息.文献[12]应用动态贝叶斯网络理论，建立光伏发电预测模型，在当前时刻各影响因素水平的条件下，预测未来短期光伏发电量的概率分布.文献[13]將预测误差分布假设为正态分布和拉普拉斯分布进行估计，预测未来短期光伏发电功率的概率分布.

本文针对不同天气状况下光伏发电功率的概率分布进行研究，直接得到发电功率的点预测值和置信区间预测值.首先采用多元自适应回归样条模型得到待预测值的先验数据作为模糊C均值算法的输入量，得到不同天气状况下的相似样本，同时筛选出重要变量作为弯曲高斯过程模型的新输入集.最后，将得到的95%置信区间预测值和点预测值与应用高斯过程估计和神经网络分位数估计得到的置信区间预测值和点预测值进行对比分析.实验结果表明，本文所提出方法的精度更高一些.

1 变量选择和分类

1.1 多元自适应回归样条

多元自适应回归样条（Multivariate adaptive regression splines，简称MARS）是一种非线性、 非参数的回归方法，可以构造出由基函数描述的复杂非线性关系，提供具体的非线性关系公式和光伏功率预测值，同时获得变量的重要程度，从而挑选出重要变量，实现变量的约减，提高预测精度.由文献[14]可知，相比于普通的预测方法，如SVR，KNN，ARMAX模型，MARS模型具有较高的预测精度，可以提高相似样本的选择正确率.因此本文选择MARS模型作为前期的预测模型.MARS的基本思想是构造一个由基函数（Basis function，简称BF）来近似描述复杂非线性关系的回归模型.

MARS模型以一组基函数组合的形式来拟合待预测的函数关系（x），定义如式（1）所示：

=（x）=α0+∑Mi=1αiBFi（x）（1）

式中：是输出变量的预测值；α0是常数；M是基函数个数；BFi（x）和αi分别是第i个基函数和相应的系数.

常见的基函数表达式如式（2）所示.

BF=max（0，x-c）=x-c，x>c；0，otherwise.（2）

式中：c是节点.当x

MARS算法分为前向过程、后向剪枝过程和模型选取三个步骤.

前向过程：模型的初始基函数集只包含一个常数项，然后MARS模型通过重复的将一对基函数加进模型，找到模型残差平方和最大减少的基函数对，从而使模型的精度得到最大限度的提高.MARS算法通过判断MSE的变化来判断模型性能是否得到改善.迭代过程一直持续，直到残差平方和足够小而不发生变化为止，或者达到用户设定的基函数个数最大值Mmax.

后向剪枝过程：剪枝过程根据广义交叉验证（GCV，Generalized Cross Validation）准则进行，

GCV（M）=1n∑ni=1（yi-i）21-C（M）n2（3）

式中：M是非常数的基函数数目；n是样本数；C（M）=M+1+dM；yi是训练数据的因变量；i是模型的预测值；d为惩罚因子，常取为3.前向过程通常会建立一个过度拟合的模型，虽然对于建模的数据拟合程度很高，但对于新数据的预测精度比较低，因此需要通过后向剪枝过程将造成模型过度拟合的基函数删除，每步删除一个使GCV值降低最大或者增加最小的基函数，最终得到多个复杂度不同的模型.

模型选取：选出GCV值最小的一个子模型作为最终的输出模型.

变量的选择：模型建立以后，就可以估计自变量对模型的重要程度.由于每个自变量可以加入到不同的基函数中，每次去掉一个变量，保留其他变量，然后计算这个去掉变量对模型拟合程度的减少量.对模型拟合度减少量最大的变量被赋予最重要的权重（100%的权重），对于其他变量则根据各自对模型拟合程度的贡献度赋予相应的权重，对模型不重要的变量赋予0%的权重.通过变量的选择，就可以将高维数据约减到低维数据，选取主变量因素，提高预测精度和效率.

1.2 模糊C均值聚类法

在光伏发电功率预测研究中，训练样本的选择对于预测结果的准确性有很大的影响，当不同时期的天气状况相似的时候，其对应的光伏发电功率也会接近，本文采用聚类的方法进行相似样本的选择.由于光伏发电功率受多种天气变量共同影响，若类型分类太多，对于分类准确度的要求增高，分类错误率会增大，同时会导致每种类型样本数过少，影响模型预测准确性，因此将其合并为具有代表性的两类，分别对应于晴天、阴天两种天气类型，其中由于雨雪等天气的功率值都比较小，属于阴天类型，将其归于阴天一类.

模糊聚类[15]就是将n个样本划分为c类.在模糊划分中，每个样本并不是严格的被划分为某一类，而是按照一定的隶属度属于某一类.

定义目标函数

J（U，V）=∑nk=1∑ci=1umikd2ik（4）

式中：uik为第k个样本属于第i类的隶属度，U为隶属度矩阵；V是聚类中心；umik是权重，为隶属度的m次方；dik是样本到聚类中心的距离.

模糊C均值聚类法的聚类准则是求U和V，使J（U，V）取最小值.具体步骤如下所示：

1）确定类的个数c，幂指数m>1和初始隶属度矩阵U（0），常取为[0，1]上的均匀分布随机数.令l=1，表示第一步迭代.

2）计算第l步的聚类中心V（l）

v（l）i=∑nk=1（u（l-1）ik）mxk∑nk=1（u（l-1）ik）m，i=1，2，…，c（5）

3）修正隶属度矩阵U（l），计算目标函数J （l）.

u（l）ik=1∑cj=1d（l）ikd（l）jk2m-2，i=1，…，c，k=1，…，n（6）

J（l）（U（l），V（l））=∑nk=1∑ci=1（ulik）m（dlik）2（7）

式中：d（l）ik=‖xk-v（l）i‖.

4）对于给定的隶属度终止容限εu>0，目标函数终止容限εj>0，最大迭代步长Lmax，当max{|u（l）ik-u（l-1）ik|}<εu或|J（l）-J（l-1）|<εJ或l>Lmax时，停止迭代，否则l=l+1，回到步骤2）.

经过上述步骤后，就可以求得最终的隶属度矩阵U和聚类中心V，使得J（U，V）的值最小.根据隶属度矩阵U中元素值就可以确定样本的类别，当uik=max1≤i≤c{uik}时，可将样本xk归为第j类.

2 基于弯曲高斯过程的概率估计

2.1 弯曲高斯过程

高斯过程回归（Gaussian process for regression，简称GPR）模型[16]是非参数的非线性回归模型，是一种概率分布估计模型，不仅可以获得点预测值，还可以获得置信区间预测值.针对本文研究的光伏发电功率预测问题，应用弯曲高斯过程模型，可以实现光伏发电功率的概率分布预测，获得更为全面的信息.基本思路是假设训练样本服从高斯分布，利用贝叶斯理论计算出相应的后验概率，然后利用最大似然法则求出相应的最优超参数，最后利用得到的模型去预测测试样本，得到待预测变量的概率分布.

假设有n个训练样本的数据集D=（X，y），其中X表示n×d维输入矩阵，y表示相应的输出变量，在标准高斯过程中，假设输入矢量和输出变量之间关系为：

yn=f（xn）+εn（8）

式中：yn是观测值；εn是噪声，εn～N（0，σ2n）.

观测值的协方差为cov（y）=K+σ2nI，观测值的先验分布为

y～N（0，K+σ2nI）（9）

式中：K是n×m核函数矩阵，Knm=k（xn，xm），k是核函数.

观测值y与测试值f*的联合分布可记为

yf*～N0，K（X，X）+σ2nIK（X，X*）K（X*，X）K（X*，X*）（10）

式中：假如有n个训练数据，m个测试数据，K（X*，X）表示测试点和训练点的m×n维协方差矩阵.预测值的后验分布即高斯回归预测方程为

f*|X，y，X*～N（*，cov（f*））（11）

式中：

*=E[f*|X，y，X]=K（X*，X）[K（X，X）+σ2nI]-1y；

cov（f*）=K（X*，X*）-K（X*，X）[K（X，

X）+σ2nI]-1*K（X，X*）

*=*，2*=cov（f*）分別为预测值f*的均值和方差.

本文选择常用的自相关平方指数作为协方差函数，如式（12）所示.

k（xp，xq）=σ2fexp-12l2‖xp-xq‖2+σ2nδpq（12）

式中：xq，xp是训练集或测试集的变量；l，σf，σn为将要被学习的超参数；δpq是符号函数.

GP模型通过最大化对数边缘似然函数来最优化超参数θ.

logp（y|X，θ）=-12yT（K+σ2nI）-1y-

12log|（K+σ2nI）|-N2log2π（13）

式中：K为协方差矩阵.

但是在一些实际情况中，观测值y和噪声ε并不是高斯分布，例如本文研究的光伏发电功率由于受太阳辐照度、温度等多种天气变量的影响并不符合高斯分布.弯曲高斯过程[17]（Warped gaussian process，简称WGP）引入了一个非线性单调弯曲函数g（y；ψ），利用弯曲函数将观测值y转换为隐性变量u，而隐性变量符合标准的高斯分布，可以应用高斯过程模型，因此弯曲高斯过程模型解决了光伏发电功率不是高斯分布的问题，可以应用在光伏发电功率预测问题上.弯曲函数如式（14）所示.

u=g（y；ψ）=y+∑Ii=1ajtanh（bj（y+cj））（14）

式中：y是观测值；I是常数，由引入的弯曲函数复杂性而定，常取为3；ψ={a，b，c}是将要被学习的参数.

因此，在转换后的训练集（X，u）上的对数似然函数可以写成如式（15）所示.

logp（u|X，θ）=-12g（yT）（K+σ2nI）-1g（y）

-12log|（K+σ2nI）|+∑Nn=1logg（y）y|y=yn

-N2log2π（15）

然后采用极大化似然函数的方法求解出超参数θ和弯曲函数参数ψ，完成WGP模型的训练过程.

在隐空间中，一个新测试点X*的预测分布符合标准高斯分布：

p（u*|x*，D，θ）=N（*（θ），σ2*（θ））（16）

然后就可以通过弯曲函数得到原始观测空间的预测概率分布：

p（y*|x*，D，θ，ψ）=

g′（y*）2πσ2*exp-（g（y*）-*）22σ2*（17）

2.2 Bagging集成学习算法

集成学习算法是机器学习领域的一个热点，该算法通过将一系列有差异的预测精度较低的基学习器（弱学习器）进行组合，构造成具有高预测精度的强预测器.弯曲高斯过程模型是一种基预测器，可以采用集成学习的方法增强模型的稳定性和预测性能.本文采用Bagging集成学习方法[18].Bagging算法的基本思想是让学习算法训练K轮，每轮的训练集Di通过在原始训练集D上随机抽取的方式获取，某个初始训练样本在某轮训练集中可以出现多次或根本不出现.然后利用由不同训练集训练出来的预测器Fi进行预测，最后采用对输出求均值或对不同输出赋予不同权重求和的方法得到最终强预测器的输出结果.Bagging方法适合于高斯过程模型的集成[19].endprint

Bagging集成学习法包括三步：创建多个训练子集，构建多个子预测器，组合成强预测器.步骤流程图如图1所示：

3 光伏出力概率预测流程

BMARS-WGP模型是一个结合了MARS模型、模糊C均值算法、WGP模型和Bagging算法的混合模型.

光伏出力预测流程如下：

1）首先采用公式y=x-min（x）max（x）-min（x）将原始数据做归一化处理，作为MARS模型的输入，得到预测值的先验数据，同时筛选出重要变量，实现原始数据的降维.

2）将选择出的重要变量X*组成新的变量集，利用模糊C均值算法将预测值的先验数据分为晴天和阴天两种不同天气状况.

3）将新变量子集c作为弯曲高斯过程模型的输入.

4）应用Bagging集成算法将K个子弯曲高斯过程模型按照权重法组合成一个强弯曲高斯过程模型，最后应用得到的模型实现测试集数据的预测，得到测试输出的点预测值和区间预测值.其中各子模型的权重为：

αk=1（RMSE）ksum1RMSE（18）

式中：（RMSE）k为第k个子模型的均方根误差值.

光伏发电功率预测的BMARS-WGP混合模型的结构图如图2所示.

4 模型结果和讨论

4.1 光伏电站数据

混合模型的数据采用国际电气电子工程师学会能源预测工作组的太阳能预测中光伏电站2012至2014年的相关数据，其中数据包括光伏板24小时的出力值和相应的气象参数值[20-22]，该电站位于南半球，光伏板为固定式.由于在夜晚，光伏板的出力值為0，因此选取2012年5月1日到5月31日和2013年5月1日到5月31日21：00到次日08：00之间12个小时的两个月数据作为模型的训练数据，将2014年5月1日到5月31日21：00到次日08：00之间12个小时的数据作为测试数据.

4.2 预测性能评估

本文所提出的混合模型不仅能够获得点预测值，还能够获得置信区间值，因此采用不同的性能评价指标.针对点预测，采用均方根误差RMSE作为评价指标，

RMSE=∑Ni=1（yi-i）2N（19）

式中：N为测试数据个数；yi为预测值；为真实输出值.均方根误差值越小，表明模型的预测精度越高.针对区间预测，采用95%的置信区间平均宽度和可靠性参数[21]1-α值来评估区间预测的性能.

1-α=γ1-αN×100%（20）

式中：γ1-α是落入置信区间的预测值的个数；N是预测值的个数.置信区间平均宽度越窄，1-α值越大，模型性能越好.

4.3 预测结果和比较分析

4.3.1 输入变量的选择

影响光伏出力的气象因素很多，若将全部气象因素作为弯曲高斯过程回归模型的输入变量，会增加预测复杂程度，影响预测精度.为此本文通过MARS模型挑选出重要变量，简化计算，提高预测精度.

本文采用国际电气电子工程师学会能源预测工作组的太阳能预测中光伏电站2012至2014年的相关数据作为训练样本，其中数据包括光伏板每小时的出力值和12个气象参数值.在MARS模型中通过将各变量加入到不同基函数中，每次去掉一个变量，保留其他变量，计算该变量对模型拟合程度的减少量，根据变量对模型拟合程度的贡献度赋予不同的权重，通过MARS模型对12个气象参数按照重要程度进行排序.各变量的重要程度如表1所示，某些气象参数重要程度低的原因是对模型拟合程度的贡献度较低，因此被赋予了较低的权重.

变量的重要程度按照百分比表示，最重要的为100%，最不重要的为0%，从表1中可知各气象参数变量的重要程度，选取重要程度超过20%的变量作为重要变量，组成预测模型的输入变量集.其中重要变量及其定义如表2所示.

表3为变量约减前后弯曲高斯过程模型区间平均宽度和1-α值的对比结果.从表3可知，无论是晴天还是阴天，变量约减前的1-α值虽然略大于约减后的1-α值，但是变量约减前的预测区间平均宽度明显大于约减后的区间平均宽度，所以可知经过变量约减后的模型，预测准确性得到了提升，更具有实用价值.

4.3.2 结果比较分析

为充分验证所提出的混合模型有效性，选取2014年5月份中3个晴天日和3个阴天日作为测试集，同时将预测结果同高斯过程模型和BP神经网络分位数模型分别就点预测和区间预测结果分别进行对比分析.

图3为本文所提出的混合模型3个晴天日和3个阴天日的预测结果图，前3天为晴天日，后3天为阴天日，横坐标为时间，纵坐标为光伏出力，阴影部分代表95%置信区间的预测区间.从图3中可知，晴天日光照强烈，天气变化平缓，光伏出力呈现一定规律性，点预测结果较为准确，误差较小，波峰处预测区间稍宽，整体预测区间较窄，整体预测精度比较高；阴天日光照较弱，光伏出力规律性较差，点预测结果相比晴天日较差，误差较大，同时预测区间相比于晴天日较宽，整体预测精度较低.

图4 （a）（b）分别为晴天和阴天各模型的点预测结果对比图.横坐标为时间，纵坐标为光伏出力.从图4可知，晴天时刻，太阳辐射度较大，天气变化比较平缓，光伏出力和预测结果的规律性较好，各模型预测结果都能够较好地跟随光伏出力的变化，误差较小；阴天时刻，太阳辐射度较小，天气变化波动性较大，相比于晴天日，各模型都不能较好地跟踪光伏出力情况，光伏出力和预测结果的规律性较差，各模型预测误差有一定波动性.

该图与表4中的数据吻合，整体来看，各模型预测的阴天日整体精度要低于晴天日精度.

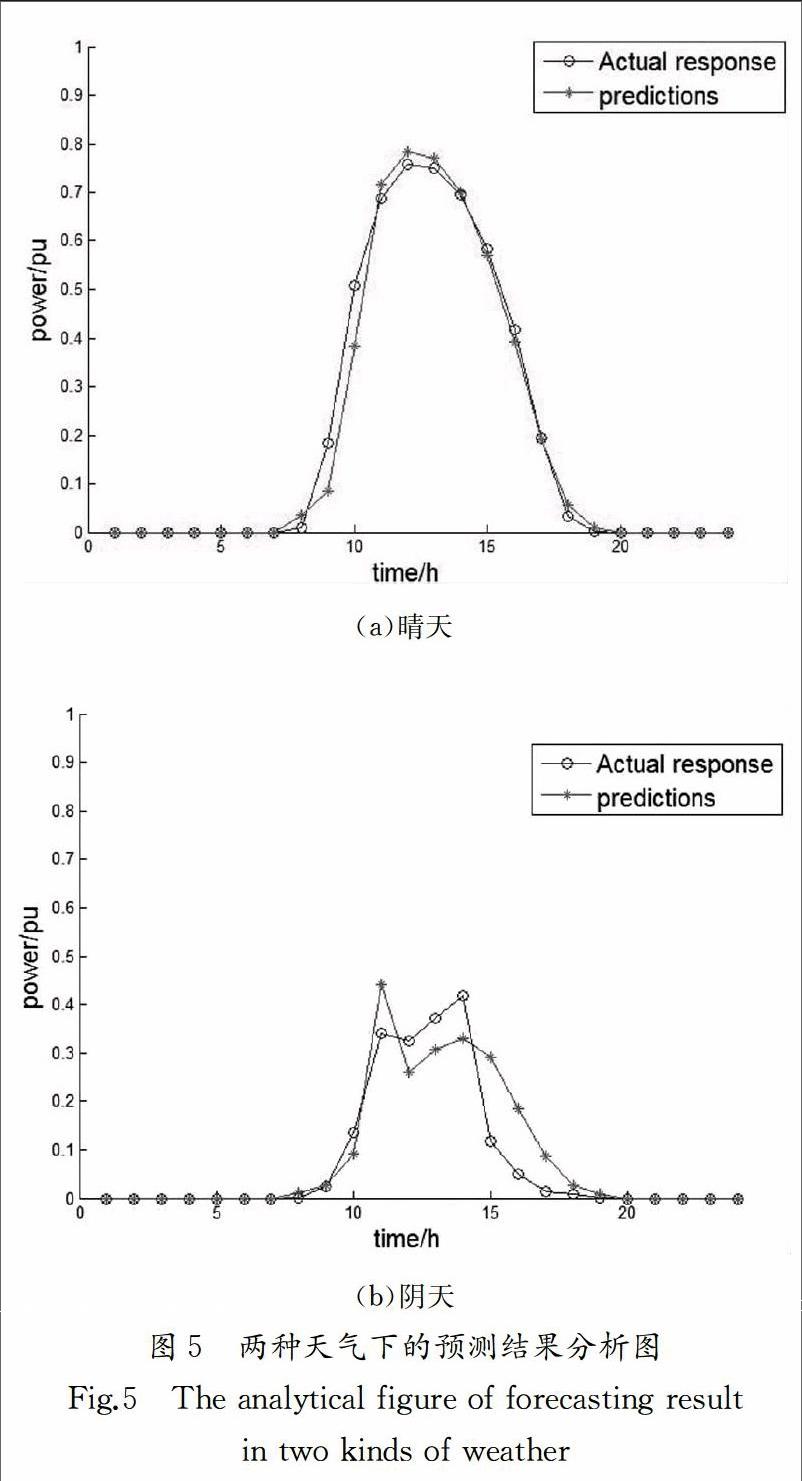
图5为光伏出力在晴天和阴天两种天气下一天的实际出力值和预测值的对比分析图.从图5（a）可知，在晴天时刻，太阳辐射度较大，天气变化比较平稳，混合模型能够较为准确地预测光伏出力情况，在7点到12点的上午时段，光伏出力呈现上升趋势，在中午时刻达到最大值，在13点到18点的下午时段，光伏出力呈现下降趋势，光伏出力整体变化较为平缓，混合模型的预测误差较小，RMSE值为5.10%；在阴天时刻，太阳辐射度较小，光伏出力变化波动相比于晴天时刻较大，同时混合模型的预测误差也相应增大，在11点到12点时间段，云量增加，天气变化明显，此时混合模型预测误差变大，在12点到14点时间段，云量稍微减少，光伏出力增加，混合模型能较好跟踪光伏出力，但14点到16点之间，云量再次增加，出现阵雨天气，天气突变，造成混合模型的预测误差增大，阴天时刻的整体预测精度较差，RMSE值为8.26%.endprint

圖6（a）和（b）分别为2014年5月13号9点和13点的光伏出力概率分布估计图，曲线为光伏出力值的概率密度曲线，加粗黑线为光伏出力实际值.从图中可以看出，光伏出力实际值都落在了模型预测区间内，曲线的峰值点与光伏出力实际值点较为接近，即光伏出力预测值与实际出力值误差较小.

图7为两个时刻不同预测方法的概率密度函数结果分析图，从图中可以看出所提出的方法（BWGP）获得的概率密度曲线尖峰薄尾的特性明显，预测结果的锐度特性更优.高斯回归方法（GP）和神经网络分位数方法（QRNN）虽然也具有尖峰薄尾的特性，但性能不如弯曲高斯模型（WGP）和所提出的方法，另外所提出的混合模型不仅考虑到光伏出力的概率分布情况，还使用集成的思想，提高了模型的性能.

表4为不同模型点预测结果的均方根误差值.由表可知，晴天日，所提出的混合模型（BWGP）的精度最高，RMSE值为0.061，其次为弯曲高斯过程模型（WGP），RMSE值为0.077，高斯过程模型（GP）RMSE值为0.080，神经网络分位数模型（QRNN）RMSE值为0.083；阴天日，各模型精度从高到低依次为混合模型、弯曲高斯过程模型、高斯过程模型、神经网络分位数模型，RMSE值分别为0.093，0.100，0.115，0.131.无论是晴天日还是阴天日，本文所提出的混合模型的点预测误差是最小的，精度是最高的.

表5为各模型的区间预测结果，其中包含两个评价指标，预测区间平均宽度和可靠性评价参数1-α，预测区间平均宽度值越小，1-α值越大，模型的实用性越高.由表5可知，本文所提出的混合模型在晴天日和阴天日的预测区间平均宽度值最小、1-α值较大，实用性最高.在晴天日，弯曲高斯过程模型和神经网络分位数模型的预测区间平均宽度值和1-α值基本一致，但在阴天日，虽然弯曲高斯过程模型预测区间平均宽度值小于神经网络分位数模型值，但是其1-α值也比神经网络分位数模型值小，两个模型各有优缺点.在晴天日，神经网络分位数模型的预测精度要稍高于高斯过程模型，但在阴天日，虽然高斯过程模型的区间宽度要低于神经网络分位数模型，但是高斯过程模型的1-α值要小于神经网络分位数模型.综合考虑，神经网络分位数模型的预测精度要高于高斯过程模型.整体而言，晴天日的预测区间平均宽度要小于阴天日值，1-α值要大于阴天日值，预测结果更加可靠，风险更低.

在电力系统规划和并网系统控制中，区间预测是对预测值包含的风险做出的合理评估，可以给电网调度人员提供可靠的数据信息，保证电网的安全稳定运行，但是预测区间平均宽度值太大，1-α值太小都会使区间预测值的实用性降低.本文所提出的混合模型的预测区间平均宽度值较小，1-α值较大，实用性较高，可以有效地反映光伏发电功率的变动特征.

5 总 结

本文提出了一种基于弯曲高斯过程的混合模型，将历史气象参数值和光伏发电功率值作为训练数据，可以实现一天内任意时刻的光伏发电功率的点预测和区间预测.利用多元自适应回归样条模型筛选出重要变量，实现了输入变量的约减，提高了区间预测的精度；利用模糊C均值法实现了对先验数据按不同天气状况的分类，得到相似样本，提高了预测的可靠性；利用Bagging学习法实现了对子预测模型的集成学习，提高了预测精度.经过实验仿真证明该方法点预测误差较小，预测区间平均宽度值较小，1-α值较大，预测精度较高，具有较高的实用性.不同天气状况对预测精度有较大的影响，下一步的工作是提高不同天气的分类准确度，进一步提高预测精度.

参考文献

[1] 龚莺飞，鲁宗相，乔颖，等.光伏功率预测技术[J].电力系统自动化，2016，40（4）：140-151.

GONG Yingfei，LU Zongxiang，QIAO Ying，et al. An overview of photovoltaic energy system output forecasting technology[J].Automation of Electric Power Systems，2016，40（4）：140-151.（In Chinese ）

[2] 李安寿，陈琦，王子才，等. 光伏发电系统功率预测方法综述[J].电气传动，2016，46（6）： 93-96.

LI Anshou，CHEN Qi，WANG Zicai，et al. Review of power forecast methods for photovoltaic generating system[J]. Electric Drive，2016，46（6）： 93-96. （In Chinese ）

[3] 丁明，王磊，毕锐.基于改进BP神经网络的光伏发电系统输出功率短期预测模型[J].电力系统保护与控制，2012，40（11）：93-99.

DING Ming，WANG Lei，BI Rui. A short-term prediction model to forecast output power of photovoltaic system based on improved BP neural network[J].Power System Protection and Control，2012，40（11）：93-99.（In Chinese ）

[4] 杨锡运，刘欢，张斌，等.组合权重相似日选取方法及光伏输出功率预测[J].电力自动化设备，2014，34（9）：118-122.

YANG Xiyun，LIU Huan，ZHANG Bin，et al. Similar day selection based on combined weight and photovoltaic power output forecasting[J].Electric Power Automation Equipment，2014，34（9）：118-122.（In Chinese ）endprint

[5] LI Yanting，SU Yan，SHU Lianjie. An ARMAX model for forecasting the power output of a grid connected photovoltaic system[J]. Renewable Energy，2014，66（6）：78-89.

[6] 丁明，徐宁舟.基于马尔科夫链的光伏发电系统输出功率短期预测方法[J].电网技术，2011，35（1）：152-157.

DING Ming，XU Ningzhou. A method to forecast short-term output power of photovoltaic generation system based on Markov chain[J].Power System Technology，2011，35（1）：152-157.（In Chinese）

[7] MANDAL P，MADHIRA S T S，HAQUE A U，et al. Forecasting power output of solar photovoltaic system using wavelet transform and artificial intelligence techniques[J]. Precedia Computer Science，2012，12（1）：332-337.

[8] 朱红路，李旭，姚建曦，等.基于小波分析与神经网络的光伏电站功率预测方法[J].太阳能学报，2015，36（11）：2725-2730.

ZHU Honglu，LI Xu，YAO Jianxi，et al. The power prediction method for photovoltaic power station based on wavelet analysis and neural networks[J]. Acta Energiae Solaris Sinica，2015，36（11）：2725-2730.（In Chinese）

[9] GIORGI M G D，MALVONI M，CONDEGO P M. Comparison of strategies for multi-step ahead photovoltaic power forecasting models based on hybrid group method of data handling networks and least square support vector machine[J].Energy，2016，107：360-373.

[10]MALVONI M，GIORGI M G D，CONDEGO P M. Photovo-ltaic forecast based on hybrid PCA-LSSVM using dimensionality reducted data[J].Neurocomputing，2016，211：72-83.

[11]王新普，周想凌，邢杰，等.一种基于改进灰色BP神经网络组合的光伏出力预测方法[J].电力系统保护与控制，2016，44（18）：81-87.

WANG Xinpu，ZHOU Xiangling，XING Jie，et al. A prediction method of PV output power based on the combination of improved grey back propagation neural network[J].Power System Protection and Control，2016，44（18）：81-87.（In Chinese）

[12]董雷，周文萍，张沛，等.基于动态贝叶斯网络的光伏发电短期概率预测[J].中国电机工程学报，2013，33（增刊）：38-45.

DONG Lei，ZHOU Wenping，ZHANG Pei，et al. Short-term photovoltaic output forecast based on dynamic Bayesian network theory[J]. Proceedings of the CSEE，2013，33（S）：38-45.（In Chinese）

[13]JUNIOR J G D S F，OOZEKI T，OHTAKE H，et al. On the use of maximum likelihood and input data similarity to obtain prediction intervals for forecasts of photovoltaic power generation[J].Journal of Electrical Engineering & Technology，2015，10（3）：1342-1348.

[14]LI Yanting，HE Yong，SU Yan，et al. Forecasting the daily power output of a grid-connected photovoltaic system based on multivariate adaptive regression splines[J].Applied Energy，2016，180：392-401.

[15]何正風.MATLAB概率与数理统计分析[M].北京：机械工业出版社，2012：277-283.

HE Zhengfeng. MATLAB probability and mathematical statistics analysis[M].Beijing： China Machine Press，2012：277-283.（In Chinese）endprint

[16]RASMUSEEN C E，WILLIAMS C K I. Gaussian Process for Machine Learning[M].MIT Press，2006.

[17]SNELSON E，RASMUSEEN C E，GHAHRAMANI Z. Warp-ed Gaussian Processes[J].Advances in Neural Information Processing Systems，2003，14： 337-344.

[18]李航.統计学习方法[M].北京：清华大学出版社，2012：137-151.

LI Hang.Statistical learning method[M].Beijing：Tsinghua University Press ，2012：137-151.（In Chinese）

[19]CHEN T，REN J. Bagging for Gaussian process regression[J]. Neurocomputing，2009，72（7/9）：1605-1610.

[20]Global energy forecasting competition 2014[EB/OL]. 2014-08-15[2017-2-13].http：//www.crowdanalytix.com/contests/global-energy-forecasting-competition-2014-probabilistic-solar-power-forecasting.

[21]HONG T，PINSON P，FAN S.Global energy forecasting competition 2012[J].International Journal of Forecasting，2014，30（2）：357-363.

[22]PINSON P，NIELSEN H A，MOLLER J K，et al. Nonparametric probabilistic forecasts of wind power： required properties and evaluation[J].Wind Energy，2007，10（6）： 497-516.endprint