基于灵敏度分析的刀形天线有限元模型修正*

徐伟杰，江 雄，张吴蔚

(中国电子科技集团公司第三十六研究所， 浙江 嘉兴 314033)

基于灵敏度分析的刀形天线有限元模型修正*

徐伟杰，江 雄，张吴蔚

(中国电子科技集团公司第三十六研究所， 浙江 嘉兴 314033)

准确可靠的有限元模型是结构动态特性分析、设计改进的基础，文中利用模态试验得到的模态参数对某刀形天线进行有限元模型修正。首先建立天线结构的参数化模型，然后通过灵敏度分析选择合适的设计参数作为后续优化对象，利用计算与试验的模态频率之间的相对误差构造加权的优化目标函数，最后应用1阶优化方法修正结构的有限元模型。修正后有限元模型的模态频率最大相对误差降低至10%以内，模态置信度(MAC)均大于0.8。该修正模型可用于后续的动力学分析。

天线；模态试验；灵敏度分析；优化；模型修正

引 言

准确可靠的动力学模型对于结构的动力响应预示和结构动态设计都具有十分重要的意义。然而在有限元建模中，模型的离散化误差、物理参数和几何尺寸的不确定性、边界条件和连接条件的简化等使理论计算结果与试验结果存在一定的偏差[1]。当偏差超过工程允许值时需要利用试验结果对有限元模型进行修正。

根据修正对象不同，有限元模型修正可分为矩阵型修正和参数型修正。矩阵型修正方法对有限元模型的质量和刚度矩阵进行修正，使得特征值和特征向量逼近试验结果，但修正后模型的物理意义不明确。参数型修正是通过调整模型的物理参数如弹性模量、材料密度、截面厚度等使分析模型与试验数据有良好的相关性，其结果具有明确的物理意义[2-4]。

本文利用某机载刀形天线的模态试验结果对有限元模型进行修正。利用计算频率与试验频率的相对误差构造目标函数，将每阶频率相对误差以及每阶振型之间的模态置信度(Modal Assurance Criterion, MAC)作为状态变量，有限元模型中的物理参数作为设计变量。先计算各阶频率和目标函数对设计变量的灵敏度，选择灵敏度较高的设计变量作为修正对象，采用合适的优化方法进行优化迭代，最后得到与试验结果更吻合的有限元模型。

1 基于灵敏度分析的模型修正方法

1.1灵敏度分析

已知有限元模型中的设计参数：

p=[p1,p2, …,pj]T

(1)

系统的特征量f是p的隐函数，当发生小变动时，特征量f的1阶Taylor展开式为：

(2)

式(2)可改写为：

SΔp≅Δf

(3)

式中：Δp为设计参数改变量，Δp=[Δp1, Δp2, …, Δpj]T；Δf为残差向量，Δf=f(p+Δp)-f(p)；S为特征量对设计参数的灵敏度矩阵:

(4)

1.2优化方法

模型修正问题一般可表述为如下的优化问题[5]：

(5)

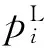
2 天线模态试验及有限元分析

首先对天线进行模态试验，利用橡皮绳将结构自由悬挂。根据结构尺寸，在天线蒙皮上共划分了24个测点，采用锤击法进行试验，使用单入多出(SIMO)法进行测试，在3个点上布置了加速度传感器。信号采样频率设置为2 400 Hz，获得频响函数后采用polyMAX方法进行参数辨识[6]，在频率范围内共识别出5阶模态参数。试验的测点布置见图1。

图1 天线模态试验测点布置

有限元建模在HyperMesh中完成，天线底座用实体单元模拟，蒙皮用壳单元模拟，蒙皮厚度自底向上逐步递减。连接螺钉用梁单元模拟，使用rbe3单元与蒙皮及底座进行连接，有限元模型见图2。由于底座刚度较大，且有限元仿真发现天线各阶模态主要表现为蒙皮的弯曲或扭转，因此试验模型中未建立底座模型。

图2 天线有限元模型

计算结果与试验结果见表1及图3，为了与试验结果对应，将计算的第3阶结果(698.5 Hz)和第4阶结果(769.5 Hz)互换。计算的模态频率均小于试验结果，相对误差最大为17.8%。各阶振型之间的MAC均大于0.8，表明振型相关性较好。

表1 有限元计算与试验结果对比

图3 天线前5阶试验模态振型

3 有限元模型修正

3.1优化模型的建立

选取材料的密度、弹性模量和各个截面的厚度作为设计变量。利用模态频率和模态振型构造状态变量，以此保证修正后模型的频率和振型与试验结果匹配。定义第i阶计算频率与第i阶试验频率之间的相对误差：

(6)

式中：fsi为第i阶计算值；fti为第i阶试验值。

同样引入MAC对计算和试验的振型进行相关性分析：

(7)

目标函数定义为：

(8)

3.2灵敏度分析结果

利用apdl语言建立的宏命令将模型导入ANSYS中并声明变量。灵敏度分析利用有限元软件中的概率设计模块完成，采用Monte-Carlo法进行模拟，共200个采样点。分析得到了结构前5阶固有频率及目标函数对各个设计参数的灵敏度。选择灵敏度较大的9个设计参数作为待修正参数。灵敏度分析结果见图4。

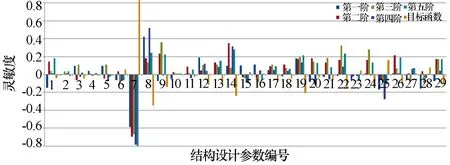
图4 灵敏度分析结果

3.3优化结果

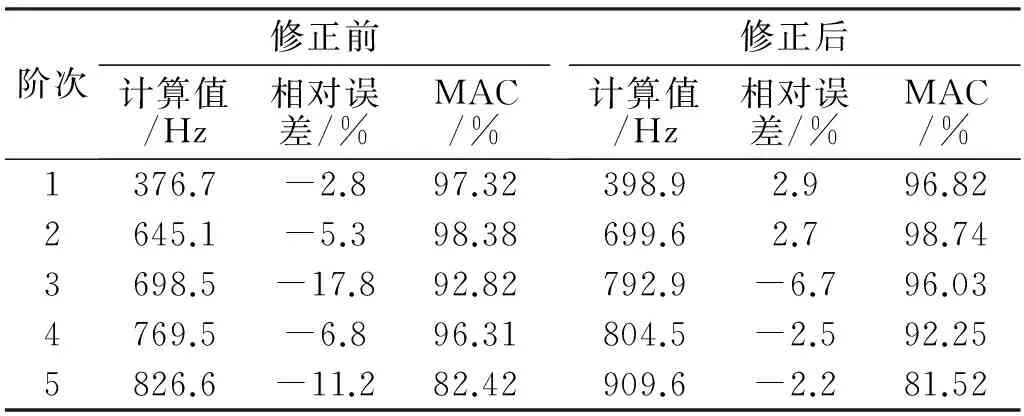
表2 优化结果

由表2可知，修正前模态频率误差较大，有两阶频率的相对误差超过了10%。修正后，各阶模态频率总体上更接近试验值，最大相对误差减小至6.7%。修正前的MAC均大于0.8，各阶振型相关性很好；修正后MAC改变很小，有限元计算的振型与试验振型仍具有很好的相关性。

4 结束语

本文通过模态试验获得了某天线结构的前5阶模态参数，有限元计算发现个别模态频率的相对误差较大。对模型进行灵敏度分析，选择对模态频率及目标函数影响较大的设计参数作为修正对象。利用ANSYS中的优化模块进行有限元模型修正，修正后模态频率的最大相对误差由修正前的17.8%降低至6.7%，各阶MAC均大于0.8。修正后的有限元模型与试验结果吻合更好，为后续的动力学分析奠定了基础。

[1] MOTTERSHEAD J E, FRISWELL M I. Model updating in structural dynamics: a survey[J]. Journal of Sound and Vibration, 1993, 167(2): 347-375.

[2] 李辉, 丁桦. 结构动力模型修正方法研究进展[J]. 力学进展, 2005, 35(2): 170-180.

[3] 秦仙蓉. 基于灵敏度分析的结构计算模型修正技术及相关问题研究[D]. 南京: 南京航空航天大学, 2001: 1-28.

[4] 常涛, 郭勤涛, 张保强. 应用模型修正方法的印制电路板参数识别[J]. 振动、测试与诊断, 2013, 33(3): 509-513.

[5] 费庆国, 张令弥, 郭勤涛. GARTEUR有限元模型修正与确认研究[J]. 航空学报, 2004, 25(4): 372-375.

[6] 傅志方. 振动模态分析与参数辨识[M]. 北京: 机械工业出版社, 1990.

徐伟杰(1972-)，男，高级工程师，主要从事电子设备结构设计工作。

江 雄(1985-)，男，工程师，主要从事电子设备结构设计工作。

张吴蔚(1988-)，女，工程师，主要从事电子设备结构设计工作。

FiniteElementModelUpdatingforKnife-edgeAntennaBasedonStructuralSensitivityAnalysis

XUWei-jie，JIANGXiong，ZHANGWu-wei

(The36thResearchInstituteofCETC,Jiaxing314033,China)

An accurate and reliable finite element model is the basis of structural dynamic analysis and design improvement. In this paper, the finite element model of a knife-edge antenna is updated based on the modal test results. First, the parametric model of the antenna is established. Then the appropriate optimization variables are selected by the sensitivity analysis. The weighted objective function is constructed by the relative errors between the calculated modal frequencies and the experimental modal frequencies. Finally, the first order optimization method is used to update the finite element model. The maximum relative error of modal frequency after model updating is reduced to less than 10%, the modal assurance criterions(MAC) are all above 0.8, the updated model can be used for subsequent dynamics simulation.

antenna; modal test; sensitivity analysis; optimization; model updating

2017-03-11

TN823+.17

A

1008-5300(2017)04-0062-03