冲击波载荷对平面阵列天线电性能的影响*

宋立伟，张 超，洪 涛

(1. 西安电子科技大学电子装备结构设计教育部重点实验室， 陕西 西安 710071；2. 西安电子科技大学天线与微波技术国家重点实验室， 陕西 西安 710071)

冲击波载荷对平面阵列天线电性能的影响*

宋立伟1，张 超1，洪 涛2

(1. 西安电子科技大学电子装备结构设计教育部重点实验室， 陕西 西安 710071；2. 西安电子科技大学天线与微波技术国家重点实验室， 陕西 西安 710071)

从机电学科交叉的角度，研究冲击波载荷作用下平面阵列天线结构塑性变形对天线电性能的影响。首先，根据爆炸冲击波的超压时程模型，采用弹塑性结构的瞬态有限元方法，获得冲击波载荷作用下平面阵列天线结构的塑性变形。然后，将结构塑性变形引入到平面阵列天线远场方向图表达式中，得到冲击波载荷作用下天线电性能的数学分析模型。最后，针对某X频段工作的平面阵列天线，分析了冲击波载荷对其增益损失、副瓣电平及波束指向的影响关系。数值分析结果可用来预测冲击波载荷作用后平面阵列天线可否正常工作。另外，文中的分析方法也可用于其他类型天线的冲击波载荷影响分析。

冲击波载荷；平面阵列天线；塑性变形；电性能

引 言

雷达天线作为电子装备的电磁传感器，已成为通信、导航、探测等雷达系统中不可或缺的重要组成部件[1-4]。若雷达天线遭到破坏，则整个雷达系统就会失效，因此雷达天线成为了导弹的直接攻击目标或重要目标。由于反辐射导弹的制导精度的限制或出于成本的考虑，反辐射导弹很难直接命中雷达天线目标，而是利用近炸引信使其战斗部在雷达上方附近爆炸。一方面导弹爆炸后高速飞散的碎片会对天线表面进行侵彻，另一方面爆炸引起的冲击波载荷将使结构发生震颤，甚至产生塑性变形，这些都将导致天线电性能恶化，甚至失效[5]。因此，雷达天线在爆炸作用下的结构毁伤和电性能的变化情况受到了越来越多的关注[6-14]。

目前，研究工作主要集中在爆炸冲击波载荷和导弹碎片对雷达天线的结构毁伤方面。文献[6]通过能量分析法和实验研究了爆炸冲击波载荷作用下圆抛物面薄壳型雷达天线的结构毁伤。文献[7]利用流固耦合法模拟了爆炸过程中相控阵天线的结构毁伤。文献[8-9]研究了不同碎片速度下天线的结构变形，以及碎片和冲击波对天线结构的复合毁伤。然而上述研究主要关注了天线结构在爆炸冲击波和碎片作用下的毁伤问题，未考虑爆炸冲击波载荷引起的结构变形对天线电性能的影响。针对这一问题，文献[10-14]研究了碎片毁伤和冲击波的变形毁伤对圆抛物面天线电性能的影响。然而他们将冲击波超压视为静载荷直接施加到天线结构上，与实际爆炸冲击波载荷的作用情况不符，另外，对于每一次计算都需要提取变形节点信息利用FEKO进行建模分析，计算相对耗时，对于在较高频段工作的天线分析更是如此。因天线在冲击波载荷作用下产生震颤，最终的塑性变形将始终存在，因此塑性变形对天线电性能的影响则更为关键。

因此，本文针对平面阵列天线在冲击波载荷作用下的塑性变形问题，给出了冲击波载荷对平面阵列天线塑性变形及电性能影响的分析方法，旨在给出冲击波载荷作用后平面天线电性能的变化情况。然后，对工作在X频段的某平面阵列天线进行了仿真分析，用以预测平面阵列天线能否正常工作。

1 冲击波载荷-塑性变形-电性能分析方法

1.1平面阵列天线塑性变形分析

炸药在空气中爆炸时将产生一系列的压缩波向四周传播，各个压缩波最终叠加成冲击波。冲击波遇到物体时发生反射，同时物体受到冲击波载荷作用发生变形甚至破坏。对于高爆炸药产生的入射冲击波的传播规律已有不少学者进行了研究，并提出了相应的经验预测方法[15-18]。一般而言，炸药爆炸产生的冲击波超压与比例距离之间存在以下关系[17]：

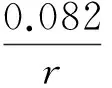
(1)

式中：r为比例距离，具体可以写为

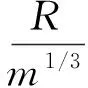
(2)

式中：R为目标距爆炸中心的距离(以下称“爆炸距离”)，m；m为炸药质量，kg。根据计算出的超压峰值结合其他冲击波参数[18]，便可确定冲击波超压时程曲线，即随时间变化的冲击波载荷F(t)，不同的炸药质量与爆炸距离可以得到不同的爆炸冲击波载荷，具有普遍意义。

天线在冲击波载荷作用下将发生震颤，甚至有可能产生不可恢复的塑性变形，因此在分析时需定义材料的塑性选项，当材料中的等效应力超过屈服点时，塑性被激活。目前常用的有限元分析软件ANSYS中，比较常用的材料塑性选项有BKIN、BISO、MKIN、MISO等，具体介绍可参见文献[19]。至于冲击波载荷作用过程中及作用之后天线整体塑性变形可以在给定合适的边界条件后利用结构动力学方程求得。

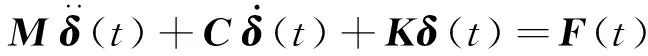
(3)

1.2平面阵列天线电性能分析

平面阵列天线是将天线单元按照一定的间距排列在一个有限的平面上，通过每个天线单元的激励电流幅度和相位，实现预定的方向图[20]。在理想情况下，平面阵列天线的远场方向图为[21]

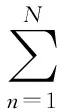
(4)

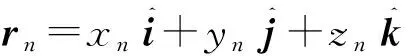
当天线受到爆炸冲击波载荷作用时，天线结构会产生变形，主要体现在背面馈电系统结构变形和阵面结构变形2种。背面馈电系统的变形将引起阵列天线单元激励幅相产生误差，当馈电系统与阵面结构分离设计时，则可不用考虑其变形引起的幅相误差[22]。阵面变形主要是阵面辐射单元的位置偏移和指向偏转，一方面使天线口径场产生新的空间相位因子；另一方面影响了天线单元自身的单元方向图，最终导致天线电性能下降。如图1所示，以阵面中某天线单元n为例，通过上述结构分析，提取其受冲击波载荷作用后产生的位置偏移Δrn=(Δx, Δy, Δz)与指向偏转ξθ,n=Δzn/Δxn和ξφ,n=Δzn/Δyn，并将这些偏差引入式(4)中，得出冲击波载荷作用之后平面阵列的远场方向图改变为

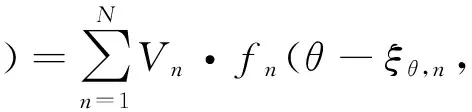
(5)

计算式(5)，便可得出冲击波载荷作用下平面阵列天线塑性变形引起的天线增益、副瓣电平、波束指向等电性能指标变化量，进行冲击波载荷作用下平面阵列天线的电性能变化情况的预测。

图1 天线单元位置变化示意图

2 数值仿真及讨论

2.1某X频段平面阵列天线

为说明冲击波载荷作用下平面阵列天线电性能的变化情况，对某X频段平面阵列天线(图2)进行了数值分析。该平面阵列天线由两液压杆支撑，阵面尺寸为2 000 mm × 1 000 mm × 25 mm，天线阵面法向与地平面夹角为30°，支撑杆为空心圆筒，其内径与外径分别为25 mm和30 mm，支撑点位置分别距阵面底部和侧边710 mm和220 mm。阵面上等间距分布的天线单元个数为133 × 50，各单元采用等幅同相激励，天线单元形式为矩形微带天线，具体单元方向性函数为[23]：

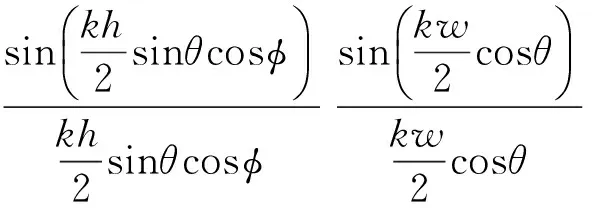
(6)

式中：h为微带天线介质基片的厚度；w为辐射元的宽度；L为辐射元的长度。

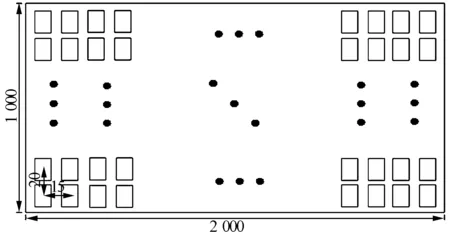
图2 平面阵列天线示意图

天线与支撑杆材料均为铝合金，其弹性模量为70 GPa，密度为2.7e3 kg/m3，泊松比为0.3。由于在冲击波载荷作用下，天线将发生塑性变形，计算中设置材料的应力-应变曲线如图3所示。将天线面板底部及支撑杆底部全约束，建立了平面阵列天线的结构有限元模型，如图4所示。

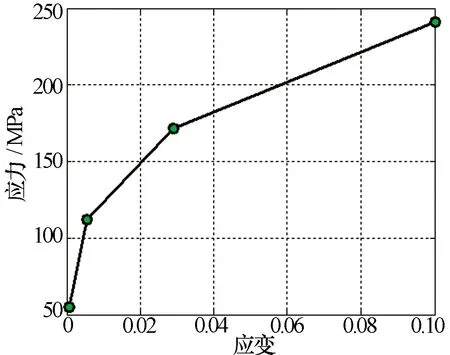
图3 材料应力-应变曲线

图4 有限元分析模型

2.2仿真结果及讨论

由于实际爆炸冲击波作用情况极其复杂且较难获取，为简化计算，本文在进行冲击波载荷作用下平面阵列天线的电性能分析时，定义的冲击波载荷时程曲线如图5所示，其中超压ΔP是根据炸药质量和爆炸距离利用式(1)换算所得。分析时取t1= 0.4 s、t2= 1 s、t3= 600 s。

图5 冲击波载荷时程曲线

2.2.1 不同爆炸距离时的结果

当炸药质量为10 kg时，不同爆炸距离下的天线塑性变形及主要电性能指标变化情况如图6和图7所示。

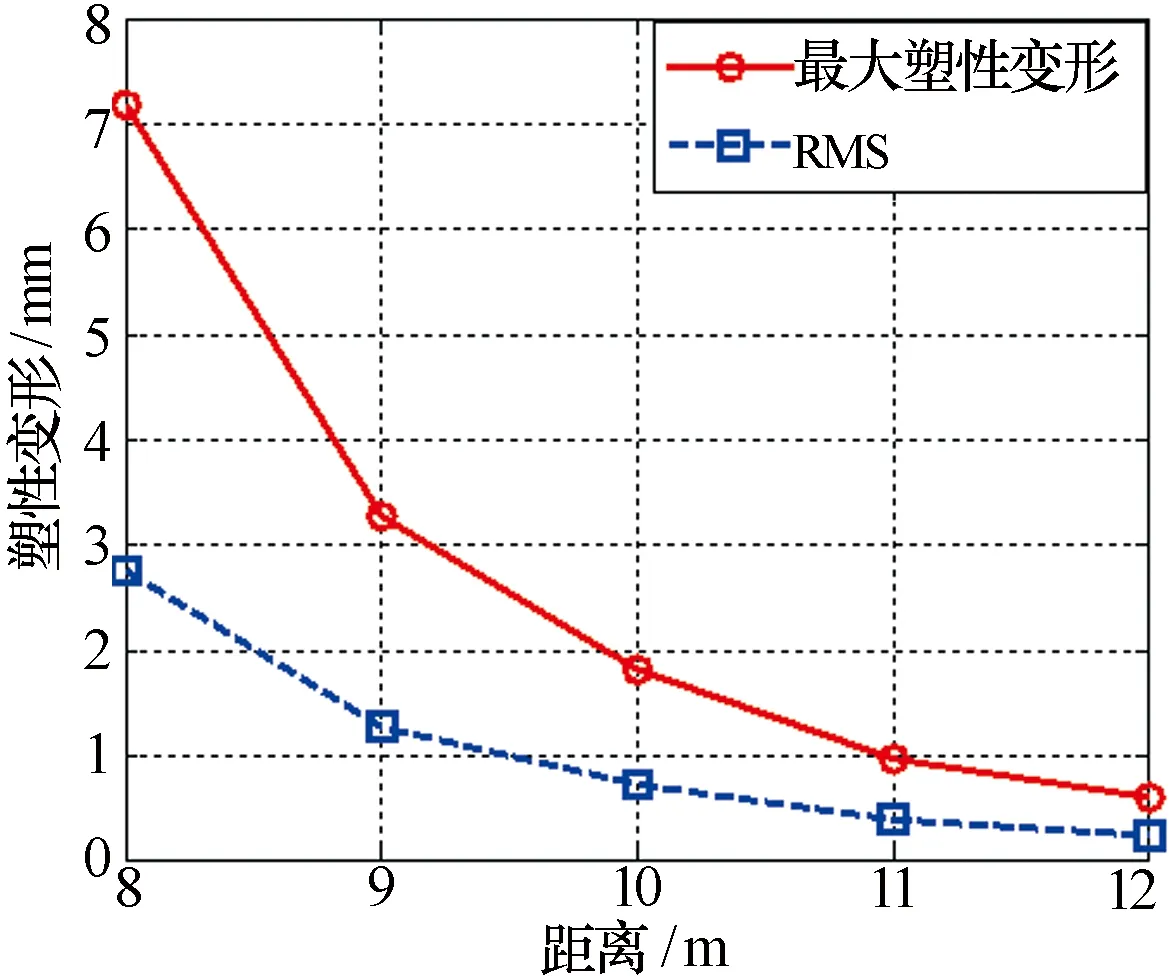
图6 爆炸距离对天线塑性变形的影响

图7 爆炸距离对天线电性能的影响

由图6可知，炸药质量相同时，天线最大塑性变形及阵面的均方根(Root Mean Square, RMS)随着爆炸距离的增加而减小。由图7可知，天线主要电性能指标(增益、副瓣、波束指向误差)变化量也随着爆炸距离的增加而减小，且副瓣电平抬升量对爆炸距离尤为敏感。

为了定量地分析不同爆炸距离下天线的塑性变形及电性能的变化情况，将炸药质量为10 kg时不同爆炸距离下天线的塑性变形及电性能数据分别列于表1和表2。

表1 不同爆炸距离下天线塑性变形情况

由表1可知，当炸药质量相同时，爆炸冲击波超压随着爆炸距离的增加而减小，爆炸冲击波作用后平面阵列天线的结构塑性变形也相应减少。如表1中爆炸距离为12 m时，天线最大塑性变形和阵面RMS分别仅为爆炸距离为8 m时的8.20%和8.32%。

表2 不同爆炸距离下天线电性能变化情况

由表2可知，天线阵面变形后，相应地引起天线电性能指标的变化，主要表现为增益下降、副瓣抬升、波束指向发生变化，且这种变化量随着爆炸距离的增加而减小。如表中爆炸距离为12 m时，E面增益损失和副瓣电平抬升量仅为爆炸距离为8 m时的0.78%和0.59%，H面波束指向偏差仅为距离为8 m时的8.96%。值得注意的是，天线变形之后，E面波束指向与理想情况相同，而H面指向发生较大变化。这是因为当冲击波载荷沿天线阵面法向作用时，天线阵面主要发生沿x轴的偏转，yoz平面(H面)方向图发生整体偏转。

2.2.2 不同炸药质量时的结果

同样地，在爆炸距离固定为10 m的情况下，不同炸药质量下的天线变形及主要电性能指标变化情况如图8和图9所示。

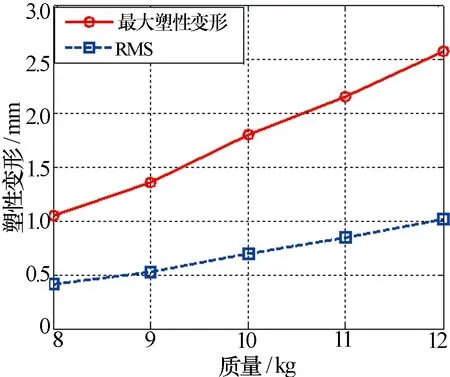
图8 炸药质量对天线塑性变形的影响

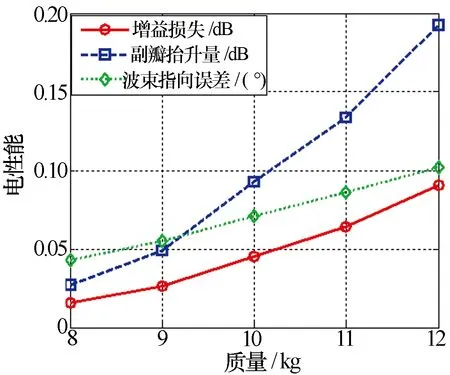
图9 炸药质量对天线电性能的影响

由图8可知，爆炸距离相同时，天线最大塑性变形及阵面RMS随着炸药质量的增加而增大。由图9可知，天线主要电性能指标变化量也随着炸药质量的增加而增大，且副瓣电平抬升量对爆炸距离尤为敏感。

为了定量地分析不同炸药质量下天线的变形及电性能变化情况，将爆炸距离为10 m时不同炸药质量下天线的变形及电性能数据列于表3和表4。

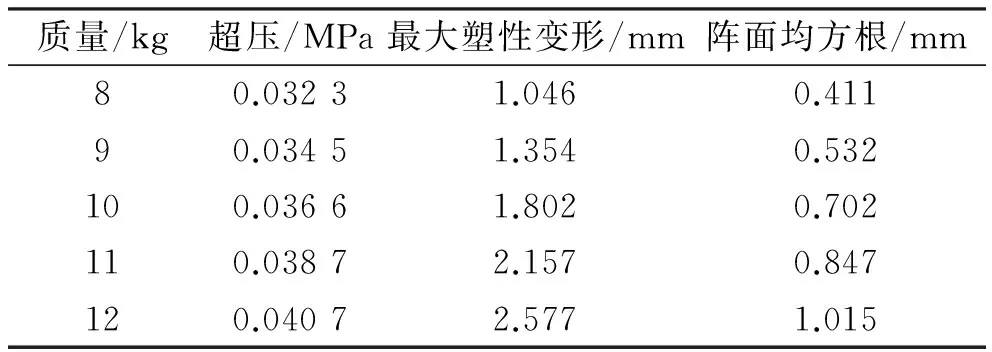
表3 不同炸药质量下天线塑性变形情况

由表3可知，爆炸距离相同时，爆炸冲击波超压随着炸药质量的增加而增大，爆炸冲击波作用后平面阵列天线的结构塑性变形也相应增加。如表中炸药质量为8 kg时，天线最大塑性变形和阵面RMS分别为炸药质量为12 kg时的40.59%和40.49%。

表4 不同炸药质量下天线电性能变化情况

由表4可知，天线阵面变形后，相应地引起天线电性能指标的变化，主要表现为增益下降、副瓣抬升、波束指向发生变化，且这种变化量随着炸药质量的增加而增加。如表中炸药质量为8 kg时，E面增益损失和副瓣电平抬升量为炸药质量为12 kg时的17.78%和13.99%，H面波束指向偏差为炸药质量为12 kg时的42.16%。

综上所述，天线最大塑性变形及阵面RMS随爆炸距离的增加而减小，随炸药质量的增加而增大。相应地，主要电性能指标变化量随爆炸距离的增加而减小，随炸药质量的增加而增大，且副瓣电平变化较为显著。

3 结束语

本文分析了爆炸冲击波载荷作用下平面阵列天线塑性变形及电性能情况。以某X频段平面阵列天线为例，计算了冲击波载荷作用下的结构塑性变形及远场辐射特性(增益、副瓣及波束指向)变化，给出了不同爆炸距离和炸药质量对平面阵列天线塑性变形及其电性能的影响。

本文的研究工作可用来预测爆炸冲击载荷作用下平面阵列天线能否继续正常工作，也可为双方对抗时，根据一方导弹跟踪精度及装药质量等指标折算出另一方雷达天线布置的安全距离提供一定的指导。需指出的是，本文并未考虑导弹碎片对天线阵面的毁伤及炸药爆炸时瞬时高温对天线热变形的影响，以后可就此展开进一步的工作。

[1] 徐东海. 天基预警雷达天线轻量化技术研究[J]. 电子机械工程, 2008, 24(5): 26-27.

[2] RAHMAT-SAMII Y, HUANG J, LOPEZ B, et al. Advanced precipitation radar antenna: array-fed offset membrane cylindrical reflector antenna[J]. IEEE Transactions on Antennas and Propagation, 2005, 53(8): 2503-2515.

[3] WANG W Q. Overview of frequency diverse array in radar and navigation applications[J]. IET Radar, Sonar and Navigation, 2016, 10(6): 1001-1012.

[4] 吴秉横, 纪奕才, 方广有. 带反射腔的分布式电阻加载探地雷达天线设计与分析[J]. 雷达学报, 2015, 4(5): 538-539.

[5] 印骏, 谭玲, 谭绍杰. 美军无人机的作战应用及其发展趋势[J]. 飞航导弹, 2010(8): 26-29.

[6] 赵文杰, 蒋浩征, 王秀兰. 爆炸冲击波对圆抛物面薄壳型雷达天线毁伤效应研究[J]. 弹箭与制导学报, 2000(1): 8-13.

[7] 任秀敏. 冲击波作用下典型相控阵天线毁伤效应研究[D]. 北京: 北京理工大学, 2015.

[8] LV Y, SHI Q, WANG G, et al. Dynamic finite-element simulation on the phased array radar antenna multiplex damage by fragment and shock wave[C]// 2012 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering (ICQR2MSE), IEEE, 2012: 929-933.

[9] 吕勇, 石全, 钱芳, 等. 不同时序破片和冲击波对天线的复合毁伤分析[J]. 火力与指挥控制, 2014, 39(3): 128-132.

[10] 袁俊明, 张庆明, 刘彦. 爆炸冲击波作用下变形毁伤对圆抛物面天线电性能影响的数值模拟[J]. 北京理工大学学报，2009, 29(S1): 86-89.

[11] 袁俊明, 张庆明, 刘彦. 破片穿孔毁伤对圆抛物面天线电性能影响的仿真计算[J]. 导弹与制造学报, 2009, 29(3): 129-132.

[12] 袁俊明, 张庆明, 刘彦. 冲击波与破片联合毁伤对反射面天线电性能影响的仿真计算[J]. 兵工学报, 2009, 30(2): 169-172.

[13] 刘彦, 袁俊明, 张庆明, 等. 冲击波作用下反射面天线辐射特性数值模拟研究[J]. 北京理工大学学报, 2009, 29(9): 763-766.

[14] LIU Y, HUANG F, ZHANG Q, et al. Calculations of radiation characteristics of reflector antennas with surface deformation and perforation[J]. Computers & Mathematics with Applications, 2011, 61(8): 2349-2352.

[15] WU C, HAO H. Modeling of simultaneous ground shock and airblast pressure on nearby structures from surface explosions[J]. International Journal of Impact Engineering, 2004, 31(6): 699-717.

[16] BRODE H L. Blast wave from a spherical charge[J]. 1959, 2(2): 217-229.

[17] 宋浦, 肖川, 梁安定, 等. 炸药空中与水中爆炸冲击波超压的换算关系[J]. 火炸药学报, 2008, 31(4): 10-13.

[18] 姚成宝, 王宏亮, 张柏华, 等. TNT空中爆炸冲击波传播数值模拟及数值影响因素分析[J]. 现代应用物理, 2014(1): 39-44.

[19] 王国强. 实用工程数值模拟技术及其在ANSYS上的实践[M]. 西安: 西北工业大学出版社, 2000: 109-114.

[20] 束咸荣, 何炳发, 高铁. 相控阵雷达天线[M]. 北京: 国防工业出版社, 2007: 1-4.

[21] 段宝岩. 电子装备机电耦合理论、方法及应用[M]. 北京: 科学出版社, 2011: 33-44.

[22] BENKO P T, LADANYI-TUROCZY B, PAVO J. A Coupled analytical-finite element technique for the calculation of radiation from tilted rectangular waveguide slot antennas[J]. IEEE Transactions on Magnetics, 2008, 44(6): 1666-1669.

[23] 魏文元, 宫德明, 陈必森. 天线原理[M]. 北京: 国防工业出版社, 1985: 147-151.

宋立伟(1981-)，男，副教授，主要从事电子装备多场耦合分析。

张 超(1992-)，男，硕士生，主要从事电子装备多场耦合分析。

InfluenceofShockWaveLoadonElectromagneticPerformanceofPlanarArrayAntennas

SONGLi-wei1，ZHANGChao1，HONGTao2

(1.KeyLaboratoryofElectronicEquipmentStructureDesign,MinistryofEducation,XidianUniversity,Xi′an710071,China；2.KeyLaboratoryofAntennasandMicrowaveTechnology,XidianUniversity,Xi′an710071,China)

Based on the theory of inter-discipline, electromagnetic performance of planar array antenna under shock wave load is explored. Firstly, the plastic deformation of planar array antenna under shock wave load is obtained by using the overpressure time-history model and elastic-plastic finite element method. Secondly, the plastic deformation is introduced into the formulation of far-field pattern of planar array antenna, then the mathematical model of electromagnetic performance of the antenna under shock wave is given. Finally, the simulation analysis of a planar array antenna operating atXband is conducted, and the gain loss, side-lobe level and beam pointing errors are obtained. The numerical analysis results can predict whether the planar array antenna is normal or not under shock wave load. Meanwhile, this analysis method can also be used to analyze the shock wave load of other types of antennas.

shock wave load; planar array antenna; plastic deformation; electromagnetic performance

2017-03-15

国家自然科学基金资助项目(51405364)

TN821+.8

A

1008-5300(2017)04-0001-05