失谐叶栅的受迫振动响应特性分析
张伟伟, 高弈奇, 全金楼, 苏丹
1.西北工业大学 翼型叶栅空气动力学国家重点实验室, 西安 710072 2.中国航发四川燃气涡轮研究院, 成都 610500
失谐叶栅的受迫振动响应特性分析
张伟伟1,*, 高弈奇1, 全金楼2, 苏丹1
1.西北工业大学 翼型叶栅空气动力学国家重点实验室, 西安 710072 2.中国航发四川燃气涡轮研究院, 成都 610500
采用基于计算流体力学(CFD)方法的降阶气动力模型并耦合结构运动方程,实现了存在外激励载荷时失谐叶栅受迫振动响应的快速分析。针对典型的跨声速叶栅,通过求解其位移响应幅值较系统地研究了失谐方式、失谐强度和叶片质量比对失谐叶栅受迫振动响应幅值的影响。研究表明文中刚度失谐形式可以改善叶栅振动的稳定性,同时导致系统受迫振动响应局部化程度的增加,并且受迫响应的最大振幅放大因子随失谐强度增加或者质量比降低存在先增大后减小的一个峰值,不同失谐形式则对这个峰值的大小有着明显的影响。由于该方法可高效地分析失谐叶栅受迫振动各参数对模态局部化的影响,在工程上有一定的应用价值。
计算流体力学(CFD); 降阶模型(ROM); 流固耦合; 失谐; 受迫响应
在航空发动机设计研制过程中,叶盘系统通常被设计成谐调的,但在实际过程中由于受到加工误差、运行中的不均匀磨损和材料性质等不确定因素的影响,叶盘结构各扇区物理或几何参数不可避免地存在偏差,称为失谐。失谐之后振动能量传递不均匀,大多集中在很少的叶片上,使叶片振幅显著增加,并使其产生高周应力,长期处于这种状态会使叶片产生高周疲劳(High Cycle Fatigue,HCF)失效,因此研究失谐振幅的放大机制、预测并控制系统的最大振动响应幅值对发动机振动设计以及提高发动机的疲劳寿命有着重要意义。
近些年,很多学者对叶盘系统的失谐振动做了相关的研究[1-3]。Campobasso和Giles[4]基于集中质量模型、利用渐进分析和矩阵摄动理论研究了N个单自由度叶片的失谐。Chol等[5]基于遗传算法的寻优方法,研究了单自由度模型弹簧振子的最佳失谐方式。王建军等[6-7]基于某典型压气机叶盘结构的有限元模型和蒙特卡罗统计方法对几何参数随机失谐叶盘结构的概率响应局部化进行了研究。Petrov[8]基于有限元降阶模型(Reduced Order Models, ROM)通过在频域内求解结构运动方程研究了失谐对受迫响应的影响。近年来,基于降阶模型的高效失谐分析方法也被越来越多的人采用。Bleeg等[9]通过矩阵的奇异值分解发展了一种新的气动弹性模型,运用该模型快速分析了一个柔性叶片转子在主动失谐后系统的气动耦合和颤振特性的变化。臧朝平等[10]提出了一种高效的失谐叶盘动力响应预测的减缩计算方法,并与实验进行了对比。
最近一些学者在研究叶栅失谐时考虑了流固耦合效应的影响[11-13],通常是在频域内求解结构运动方程而将气动力作为位移扰动的线性函数、或将气动力视为一个小量,这难以反应真实气动力耦合效应。而在时域内通过求解非定常Euler/Navier-Stokes(N-S)方程获得精确气动力来研究叶栅失谐的非常少,主要是全叶排的计算量大而且由于流动复杂获得非定常稳态结果所需的计算时间是海量的。Sadeghi和Liu[14]、郑赟和王静[15]通过在时域内计算模态气动力一个周期所做的功来研究失谐对系统颤振稳定性的影响,但只是通过少数通道的计算来确定失谐叶栅稳定性本质上是解耦分析,没有考虑到失谐对振动频率的影响;Sadeghi和Liu[16]通过直接耦合方式研究了流固耦合效应对失谐颤振稳定性的影响,采用计算通道不多,且获得振动响应的稳定解需要50个左右的计算周期,其计算所消耗的时间也非常多。
本文通过计算流体力学(CFD)计算的气动力响应数据,运用系统辨识技术构建了非定常气动力降阶模型,在状态空间内耦合存在外激励载荷的结构运动方程,构建了全叶栅失谐受迫响应的耦合气动弹性分析模型。计算了受迫振动响应的最大振幅放大因子,并研究了刚度失谐下各种参数对受迫响应特性的影响。
1 研究方法
1.1 气动力模型
本文的流固耦合分析采用文献[17-19]发展的降阶气动力模型。该方法只需少数几个相邻叶片通道的非定常CFD求解的输入输出数据,就可建立全叶栅低阶气动力状态空间模型,主要建模步骤如图1所示。
根据文献[18-19]最终得到叶栅降阶的气动力状态空间方程为
(1)

图1 叶栅颤振分析中的非定常气动力建模流程图Fig.1 Flow chart of unsteady aerodynamic modeling for cascade flutter analysis

1.2 结构模型
在拉格朗日坐标系下建立流场中叶栅的结构运动方程为

(2)
式中:M为叶栅模态质量矩阵;G为结构阻尼矩阵;K为叶栅刚度矩阵;Fa(t)=qSfa(t)为模态气动力,q为动压,S为叶片的参考面积;Fe(t)=qSfe(t)=qS[fe1(t),fe2(t),…,fej(t),…,feN(t)]为外激励力向量,fej(t)为第j个叶片的激励力系数;且
M=diag(m1,m2,…,mj,…,mN)
K=diag(k1,k2,…,kj,…,kN)
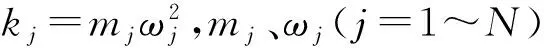
定义第j个叶片的失谐量为
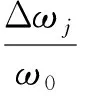
(3)
式中:ω0为叶片未失谐时的固有频率。
假设叶栅中叶片上的激励力为谐波形式,第j个叶片的激励力系数为
(4)
式中:f0为无量纲外激励力幅值;ωe为激振频率;Nd为节径数;i为虚数单位;φj为叶栅中第j个叶片的的相位。
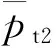
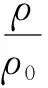
(5)
设μ和μ0分别为当前叶片质量比和“训练计算”时的叶片质量比,则有
(6)
式中:m为谐调叶片的质量;b=c/2,c为叶片的弦长。
由式(5)和式(6)可知
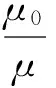
(7)
(8)
式中:
1.3 气动弹性模型
考虑到气动弹性过程是气动/结构耦合的一个不断反馈的过程,将式(1)和式(8)联立得到如式(9)所示的气动弹性方程。
(9)
令
式(9)可写为
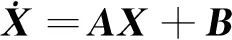
(10)
当叶栅系统无外激励力时,则式(10)为
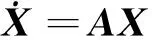
(11)
通过求解式(11)的特征值来判断叶栅系统稳定性,特征值的实部为叶栅系统阻尼项,虚部为叶栅振动频率项。
当叶栅存在外激励力时,可以通过差分方法来求解式(10)的强迫振动响应。但文中主要关注的是强迫振动幅值,不需要考虑叶栅具体的强迫振动响应过程,可根据动态线性流假设以及频域方法假定在周期性简谐外激励作用下最终的响应为一阶谐波形式,即
X=X0ei ωet
(12)
式中:X0为复数形式的初始值。
将式(12)代入式(11)可得到
X0=(iωeI-A)-1Be-i ωet
(13)
可由X0中各元素的绝对值求得各叶片位移响应的幅值。
2 算例与分析
STCF4 (Standard Test ConFiguration 4)是瑞士联邦理工学院的Bölcs和Fransson在20世纪80 年代开展的10组著名的标准叶栅气动弹性实验中的第4组[20]。这组实验公开了实验数据,常常被研究者用于叶轮机气动弹性分析方法的验证。
STCF4叶栅共有20个叶片,轮毂与外轮套直径之比为0.8,叶片安装角γ=56.65°,叶根与叶梢叶型相同,叶片弦长c=0.074 4 m,由于叶片较厚,刚度较大,所以假设叶片表面不发生结构变形,整个叶片在与之相连接的弹性梁的带动下发生弯曲振动,振动方向与弦线方向成夹角δ,叶片振动的固有频率为149 Hz,取50%叶高处的叶片截面进行计算,如图2所示。计算状态为552B实验状态:入口总压为1.714×105Pa,出口静压为1.013×105Pa,均匀入流角β1=-45°,入口静温T1=288.15 K。计算网格如图3所示,网格节点数约为1.6万,单元数为0.78万。相关文献没有给出STCF4的质量比,所以下面对质量比进行探究时,根据叶型的形状和可能的材质,估算了质量比,并选取100~800为本文的研究范围。而各个叶片的失谐比一般小于5%[21],本文选取失谐比0%~2%为研究范围。
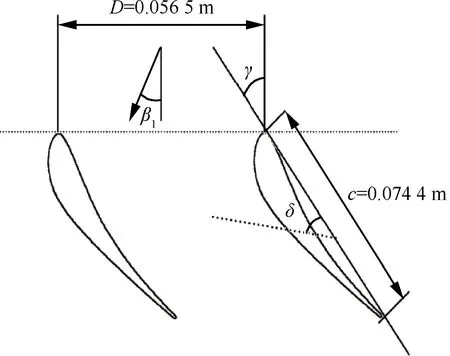
图2 STCF4模型参数Fig.2 Model parameters of STCF4
图3 STCF4通道网格Fig.3 Grid of STCF4 passage
2.1 各叶片气动力辨识结果
本文非定常CFD训练计算对中间叶片施加的都是多级训练信号,该训练信号计算时间步长较短且拥有带宽频率的范围较大。叶栅非定常气动力建模的输入量是中间叶片(0号叶片)弯曲振动模态的运动位移h,如图4所示;输入量的功率谱密度如图5所示。训练信号的频率范围需要覆盖结构振动模态的固有频率及关注频段。图中最大功率谱密度对应的中心频率与STCF4叶片弯曲振动的固有频率一致。
算例采用7个叶片通道进行计算,中间振动叶片编号为0,上游为-1,下游为1,以此类推。各个叶片气动力系数非定常响应按照文献[18]定义。求解各叶片上的非定常气动力响应并将其作为输出量,采用系统辨识技术建立气动力降阶模型。非定常气动力响应及辨识结果如图6所示,CQk为无量纲模态气动力系数。从图6可以看出,除了距离振动叶片(0号叶片)较远的叶片上的非定常气动力由于其本身数值很小而相对误差较大,其他叶片的气动力辨识结果与原气动力数值吻合得非常好。
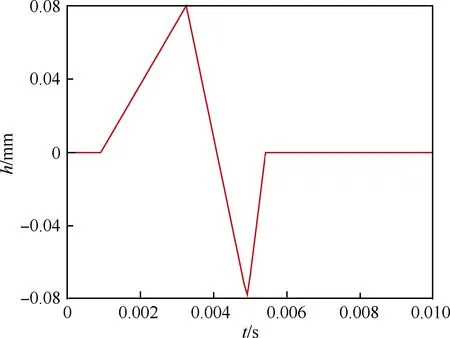
图4 CFD训练计算信号Fig.4 CFD training calculation signal
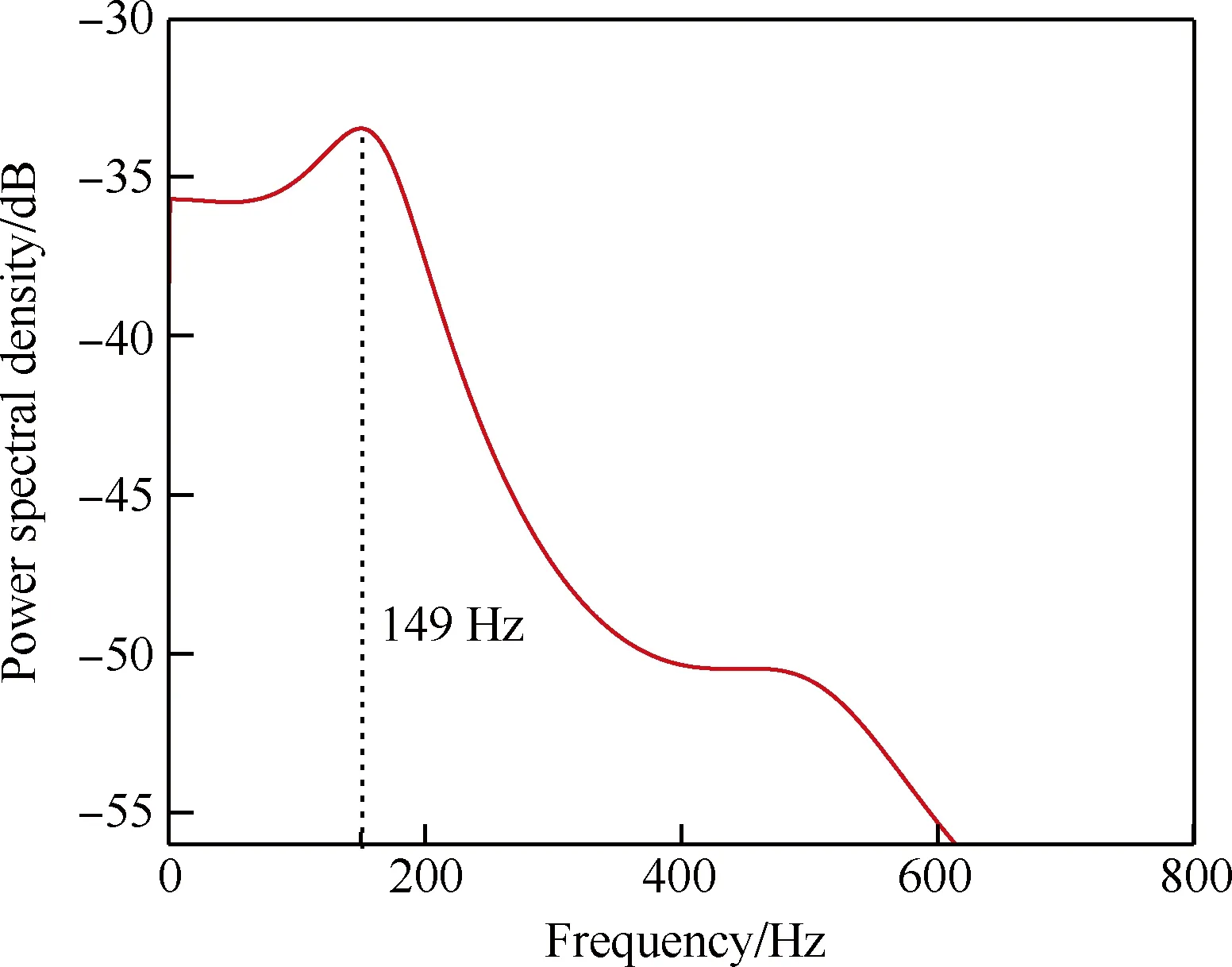
图5 训练信号功率谱密度Fig.5 Power spectral density of training signal
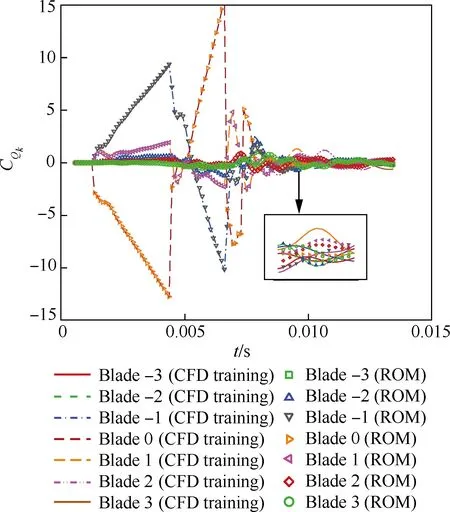
图6 训练信号的辨识结果Fig.6 Identification results of training signal
2.2 主动失谐
首先研究了2种典型主动失谐形式的叶栅受迫振动响应。如图7所示,图中直线表示谐调时叶片的刚度,柱状图表示失谐后各个叶片的刚度。失谐方式1是2个叶片组成的基本扇区圆周循环对称结构,而失谐方式2是4个叶片组成的基本扇区圆周循环对称结构。刚度较小的失谐叶片的失谐量为σj=-σ0(其中σ0为所有叶片统一的失谐比,是正常数),较大的失谐叶片的失谐量则为σj=σ0。
图8给出了在失谐比σ0=1%、叶片质量比μ=800、节径数Nd=1时叶栅的最大振幅随激振频率的变化曲线。图8中失谐后最大振幅明显变大,说明失谐使得叶栅中部分叶片受迫振动的振幅增大;同时失谐方式2的最大受迫振动的振幅相比失谐方式1更大、而且在相当大的激振频率范围内都有较大的幅值。通常定义失谐后的最大振幅与未失谐的振幅之比来描述模态局部化程度,因此失谐方式2下受迫振动的模态局部化程度相对较大。图9给出了失谐前后由式(11)计算的关键特征值分布,图9中的2种失谐形式明显地改善了系统的颤振稳定性,特征值分布由谐调时的1簇变为失谐后的2簇或者3簇,与之对应的图8中受迫振动幅值变化曲线的峰值个数一致。
图10给出了当激振频率为叶片共振频率时两种失谐方式各叶片的振幅分布。可以看出当叶栅为准周期对称结构时,各基本扇区的振幅也是周期对称的,且每个基本扇区内各叶片的振幅不同,基本扇区内某些叶片振幅急剧增大而出现不同程度的模态局部化现象,失谐方式2的受迫振动模态局部化程度更严重。另外图10中失谐方式1在共振频率附近的受迫振动幅值小于谐调叶栅的振动幅值,因此通过合理安排失谐方式可以减小受迫振动幅值,达到减振的效果。
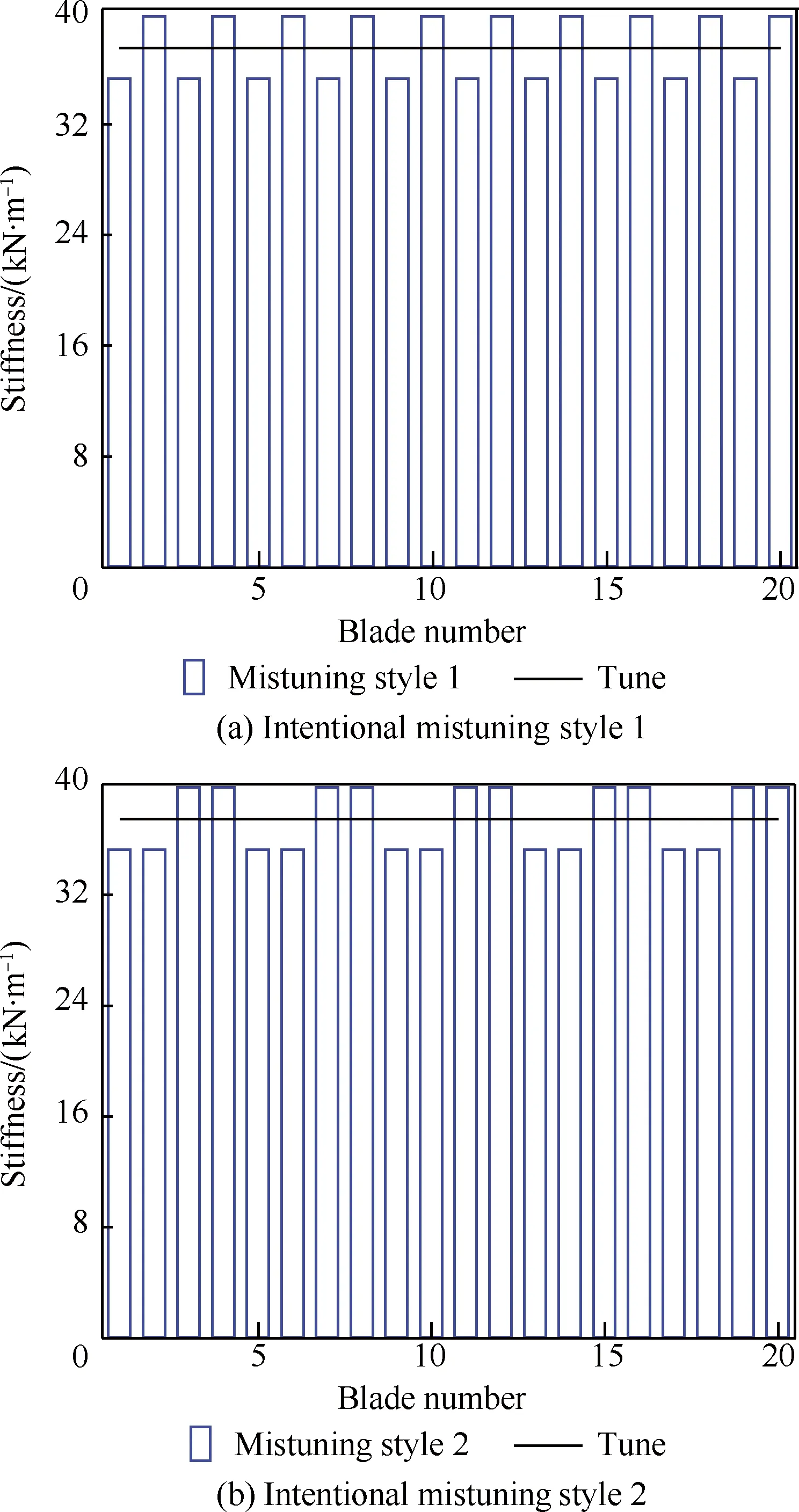
图7 2种主动失谐方式的叶片刚度分布 Fig.7 Blade stiffness distribution of two intentional mistuning patterns
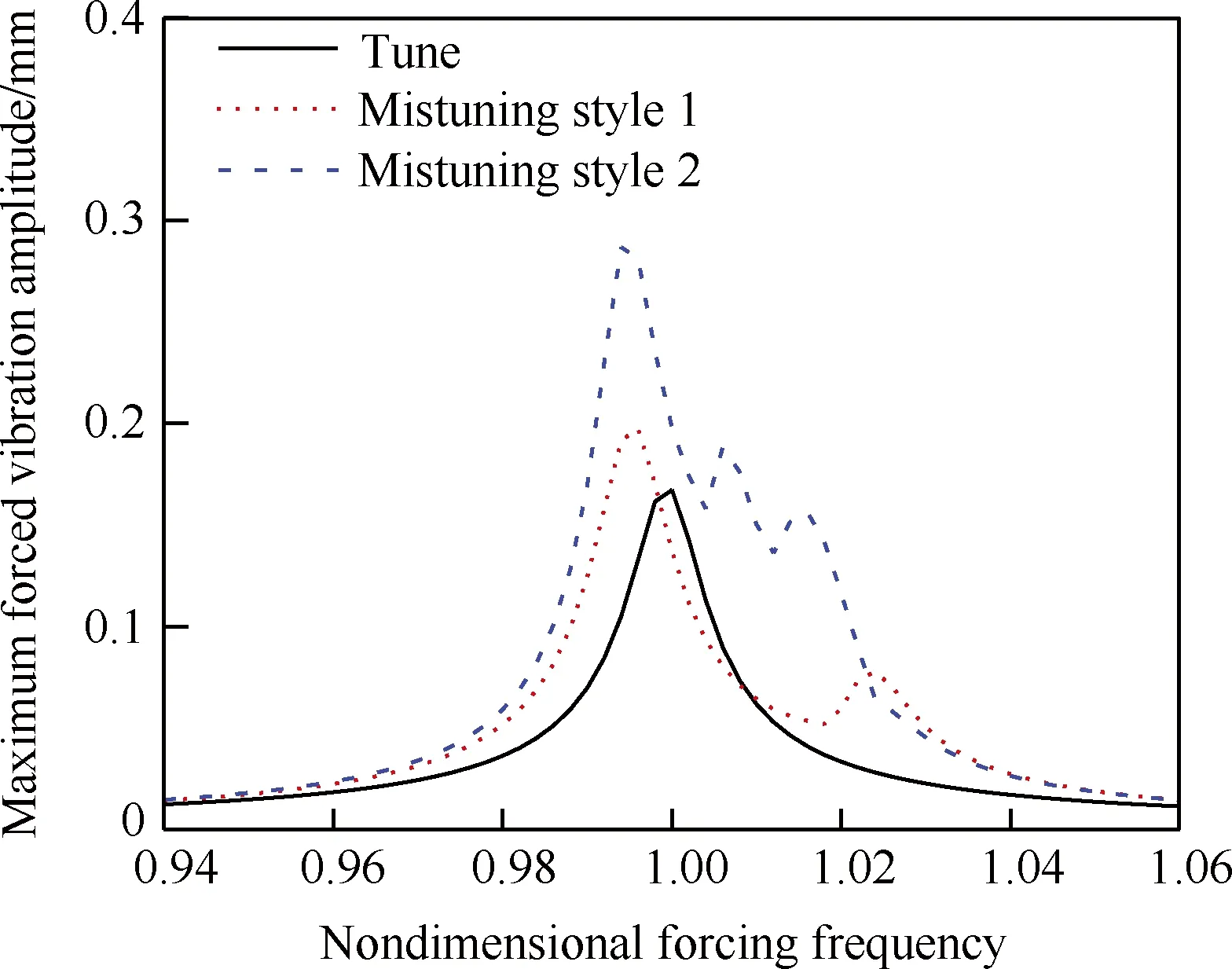
图8 最大受迫振动幅值随无量纲外激振频率的变化 Fig.8 Maximum forced vibration amplitude vs nondimensional forcing frequency
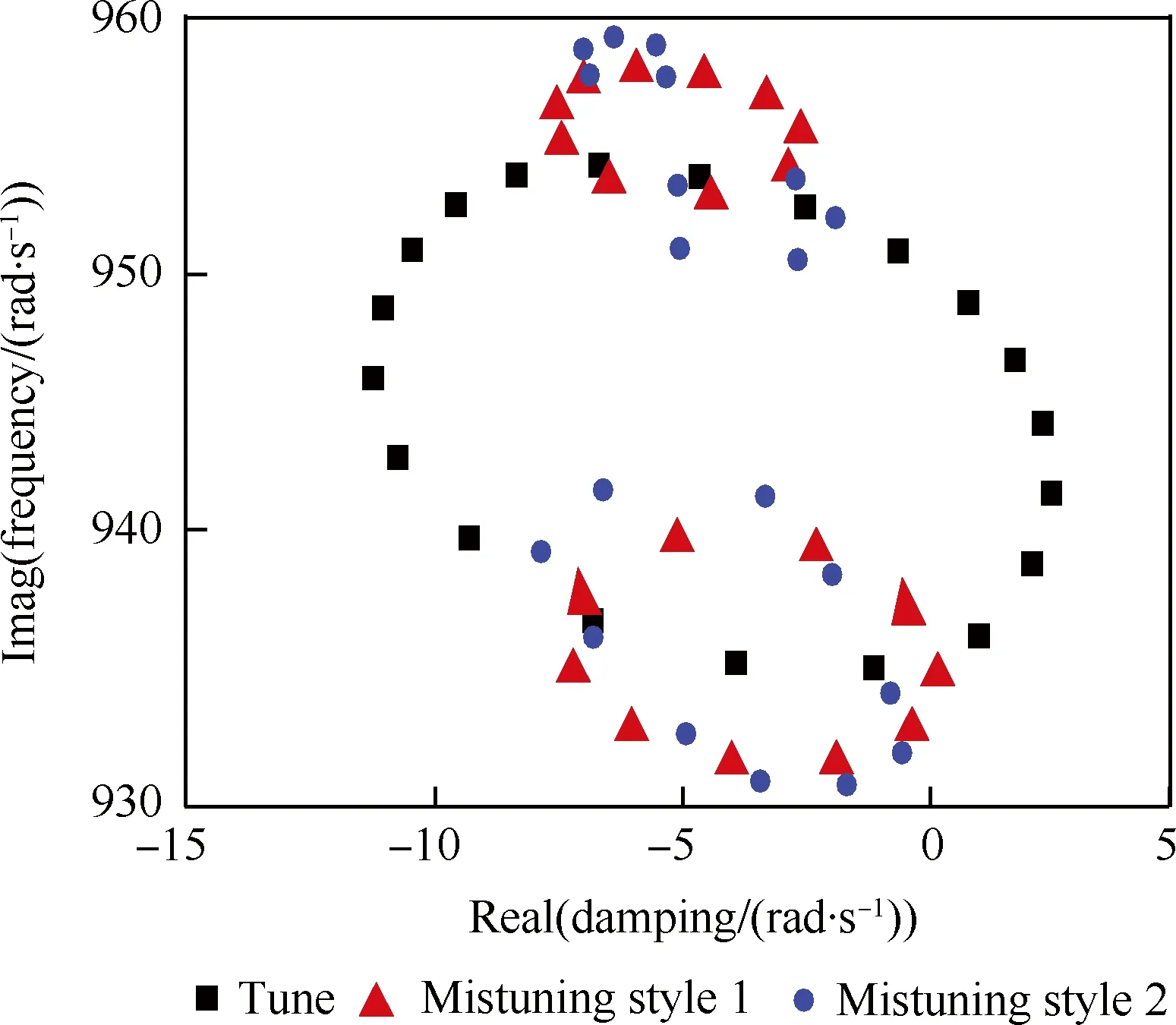
图9 叶栅失谐前后关键特征值分布 Fig.9 Distribution of crucial eigenvalues of tuned and mistuned cascades

图10 失谐前后的位移幅值分布Fig.10 Distribution of displacement amplitude of tuned and mistuned cascades
图11给出了叶片质量比μ=800、节径数Nd=1时失谐方式1的最大振幅放大因子(Amax/Atune)随失谐比的变化,其中Amax为失谐叶片的最大振幅,Atune为谐调叶片的振幅,σ0为失谐比。随着失谐比的增大叶栅的最大振幅放大因子先增大达到峰值,然后逐渐地减小,与文献[22]的结论一致。 这主要是因为随着失谐量的增大引起的局部化现象越来越严重,而当失谐比达到某一临界值后,叶栅原谐调系统破坏得非常严重,扇区内各叶片固有频率相差较大,使得叶片的振动受相邻叶片气动耦合共振影响减小。
图12给出了σ0=1%、节径数Nd=1时失谐方式1的最大振幅放大因子随叶片质量比μ的变化曲线。可以看出最大幅值放大因子随着质量比减小首先略微增加,达到峰值,然后随着流固耦合作用的增加而减小。因为质量比较大时虽然随着质量比的减小惯性力在减小并且气动力耦合作用增强,但惯性力占主导地位,叶片结构失谐使得叶片的振幅略微增大,而当质量比较小时气动力耦合越来越强。使得振动能量向四周叶片分散,使得最大振幅逐渐减小。
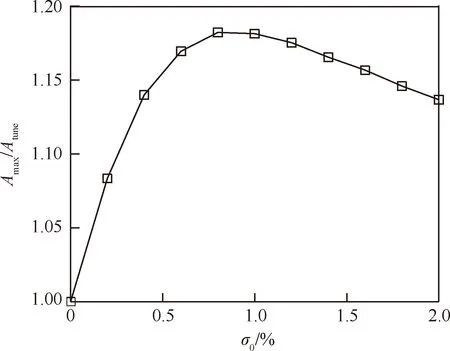
图11 最大振幅放大因子随失谐比的变化(主动失谐模式) Fig.11 Maximum amplitude magnification factor vs mistuning ratio (intentional mistuning pattern)
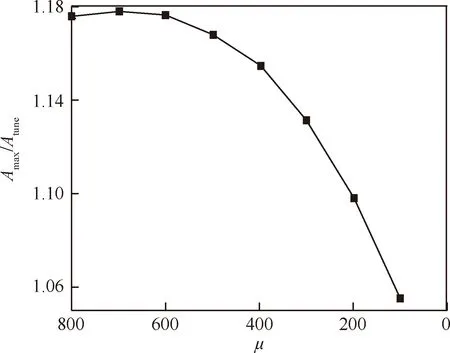
图12 最大振幅放大因子随质量比的变化(主动失谐模式) Fig.12 Maximum amplitude magnification factor vs mass ratio (intentional mistuning pattern)
上述研究表明主动失谐改善了系统的颤振稳定性,但同时带来了模态局部化现象。现今的压气机工程中,发动机叶片的设计倾向于越来越轻、薄,而叶片的表面载荷只增不减,相应的流固耦合效应也越来越明显。在本节探究质量比、失谐量对模态局部化的影响规律的过程中,提示了流固耦合作用对失谐叶栅受迫响应的规律,可为型号设计提供指导。
2.3 随机失谐
由于加工误差和使用中的磨损导致的叶片间失谐一般是随机性的,文中用蒙特卡罗方法来统计分析叶栅刚度随机失谐下系统的受迫响应特性。
考虑了2种随机失谐分布形式:一种是均匀分布,给定2种失谐叶片A和B在20个叶片中均匀随机分布,刚度较小的失谐叶片的失谐量为σj=-σ0,刚度较大的失谐叶片的失谐量则为σj=σ0,刚度分布形式之一如图13(a)所示;另外一种是正态分布,20个叶片各自的失谐量为σj=σ0Nv,其中Nv为服从(0,1)标准正态分布的随机值,刚度分布形式之一如图13(b)所示。2种随机分布的样本数都为500。
图14给出了统计分析得到的2种随机失谐方式的最大振幅放大因子随失谐量的变化趋势,计算状态为质量比μ=800、节径数Nd=1。图15给出了统计分析得到的两种随机失谐方式的最大振幅放大因子随质量比的变化趋势,计算状态为失谐比σ0=1%、节径数Nd=1。图14 和图15的变化趋势和2.2节的主动失谐是一致的,但振幅放大因子却非常大,这是因为随机失谐相当于叶排中所有叶片组成的基本扇区圆周循环对称结构包含的叶片数增多了,受迫响应的模态局部化程度相对提高了很多。图14和图15中的均匀随机分布的峰值振幅放大因子明显比正态分布的大。
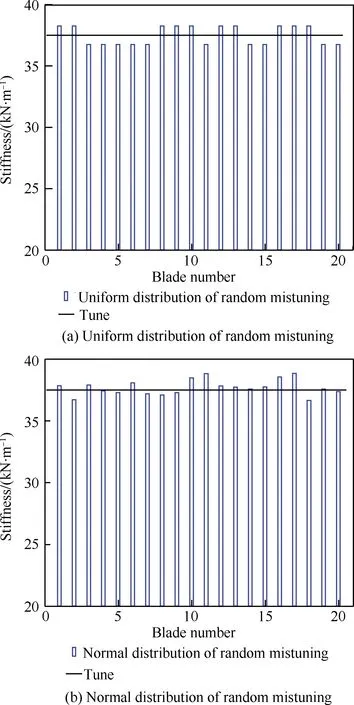
图13 2种随机失谐方式的叶片刚度分布 Fig.13 Blade stiffness distribution of two random mistuning patterns

图14 最大振幅放大因子随失谐比的变化(随机失谐模式) Fig.14 Maximum amplitude magnification factor vs mistuning ratio (random mistuning pattern)
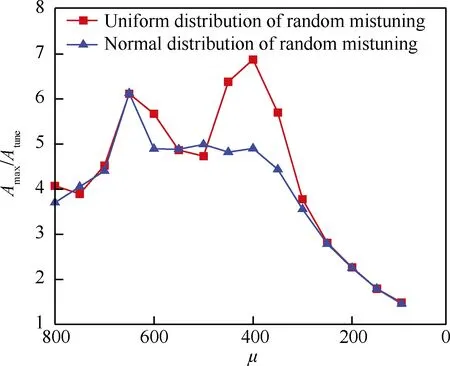
图15 最大振幅放大因子随质量比的变化(随机失谐模式) Fig.15 Maximum amplitude magnification factor vs mass ratio (random mistuning pattern)
3 结 论
基于CFD技术,建立气动力降阶模型分析叶片刚度失谐时的受迫振动幅值的变化,从主动失谐和随机失谐2个角度分析了失谐强度及叶片质量比对受迫振动幅值的影响, 结果表明:
1) 文中方法既能快速地分析失谐叶栅的稳定性,又能计算叶栅各叶片受迫振动的幅值。
2) 叶片失谐改变系统稳定性的同时也会导致受迫振动模态的局部化现象,使得少数叶片的振幅急剧增大,且局部化程度与失谐方式、失谐强度和质量比等参数有关,选择合理的参数可以改善受迫振动的局部化程度。
3) 准周期对称结构基本扇区包含叶片数越多,其受迫模态局部化程度越大,叶片的振幅放大因子也越大。
4) 主动失谐和随机失谐的最大振幅放大因子关于失谐量和叶片质量比的变化趋势是一致的,随着失谐量的增加或者叶片质量比的减小,振幅放大因子都是先增大后减小,存在一个峰值,并且峰值的大小受失谐形式的影响十分明显。
[1] LIM S H, BLADH R, CASTANIER M P, et al. Compact, generalized component mode mistuning representation for modeling bladed disk vibration[J]. AIAA Journal, 2007, 45(9): 2285-2298.
[2] MARTEL C, CORRAL R. Asymptotic description of maximum mistuning amplification of bladed disk forced response[J]. Journal of Engineering for Gas Turbines and Power, 2009, 131(2): 601-610.
[3] PIERRE C, SMITH T E, MURTHY D V. Localization of aeroelastic modes in mistuned high-energy turbines[J]. Journal of Propulsion and Power, 1994, 10(3): 318-328.
[4] CAMPOBASSO M S, GILES M B. Analysis of the effect of mistuning on turbomachinery aeroelasticity[C]//Proceedings of the IX International Symposium on Unsteady Aerodynamics, Aeroacoustics and Aeroelasticity in Turbomachines. Grenoble: Presses Universitaires de Grenoble, 2000: 885-896.
[5] CHOL B K, LENTZ J, RIVAS-GUERRA A J, et al. Optimization of intentional mistuning patterns for the reduction of the forced response effects of unintentional mistuning: Formulation and assessment[J]. Journal of Engineering for Gas Turbines and Power, 2003, 125(1): 131-140.
[6] 廖海涛, 王建军, 李其汉. 随机失谐叶盘结构失谐特性分析[J]. 航空动力学报, 2010, 25(1): 160-168.
LIAO H T, WANG J J, LI Q H. Mistuning characteristics analysis of mistuned bladed disk assemblies[J]. Journal of Aerospace Power, 2010, 25(1): 160-168 (in Chinese).
[7] 于长波, 王建军, 李其汉. 失谐叶盘结构的概率响应局部化特性[J]. 航空动力学报, 2010, 25(9): 2006- 2012.
YU C B, WANG J J, LI Q H. Probability characteristics for response localization of mistuned bladed disk assemblies[J]. Journal of Aerospace Power, 2010, 25(9): 2006-2012 (in Chinese).
[8] PETROV E P. Reduction of forced response levels for bladed discs by mistuning: Overview of the phenomenon[J]. Journal of Engineering for Gas Turbines and Power, 2011, 133(7): 1039-1051.
[9] BLEEG J M, YANG M T, ELEY J A. Aeroelastic analysis of rotors with flexible disks and alternate blade mistuning[J]. Journal of Turbomachinery, 2009, 131(1): 1-9.
[10] 臧朝平, 段勇亮, PETROV E P. 失谐叶片轮盘的减缩建模及动力响应预测方法[J]. 航空学报, 2015, 36(10): 3305-3315.
ZANG C P, DUAN Y L, PETROV E P. Reduced-order modelling and dynamic response prediction method for mistuned bladed disks[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(10): 3305-3315 (in Chinese).
[11] HE Z J, EPUREANU B I, PIERRE C. Fluid-structural coupling effects on the dynamics of mistuned bladed disks[J]. AIAA Journal, 2007, 45(3): 552-561.
[12] PETROV E P. A method for forced response analysis of mistuned bladed disks with aerodynamic effects included[J]. Journal of Engineering for Gas Turbines and Power, 2010, 132(6): 1-10.
[13] REDDY T S R, MIN J B, TRUDELL J J. Mistuned bladed disk analysis with unsteady aerodynamics using turbo-REDUCE[C]//Proceedings of the 46th AIAA/ASME/ASCE/AHS/ASC Structures, Structual Dynamics & Materials Conference. Reston, VA: AIAA, 2005.
[14] SADEGHI M, LIU F. Computation of mistuning effects on cascade flutter[J]. AIAA Journal, 2001, 39(1): 22-28.
[15] 郑赟, 王静. 错频对叶片的气动弹性稳定性的影响[J]. 航空动力学报, 2013, 28(5): 1029-1036.
ZHENG Y, WANG J. Influence of frequency mistuning on aeroelastic stability of blade[J]. Journal of Aerospace Power, 2013, 28(5): 1029-1036 (in Chinese).
[16] SADEGHI M, LIU F. Investigation of mistuning effects on cascade flutter using a coupled method[J]. Journal of Propulsion and Power, 2007, 23(2): 266-272.
[17] 苏丹, 张伟伟, 张陈安, 等. 基于系统辨识技术的叶轮机非定常气动力建模方法[J]. 航空学报, 2012, 33(2): 242-248.
SU D, ZHANG W W, ZHANG C A, et al. An unsteady aerodynamic modeling for turbomachinery based on system identification[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(2): 242-248 (in Chinese).
[18] 苏丹, 张伟伟, 全金楼, 等. 基于CFD计算的高效叶栅耦合颤振分析方法[J]. 航空学报, 2014, 35(12): 3232-3243.
SU D, ZHANG W W, QUAN J L, et al. An efficient coupled method of cascade flutter analysis by using CFD technique[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(12): 3232-3243 (in Chinese).
[19] SU D, ZHANG W W, YE Z Y. A reduced order model for uncoupled and coupled cascade flutter analysis[J]. Journal of Fluids and Structures, 2016, 61: 410-430.
[20] BÖLCS A, FRANSSON T H. Aeroelasticity in turbomachines—Comparison of theoretical and experimental cascade results[R]. Lausanne: Communication du LTATEPEL, 1986.
[21] 王建军, 李其汉, 朱梓根. 失谐叶片-轮盘结构系统振动局部化问题的研究进展[J]. 力学进展, 2000, 30(4): 517-528.
WANG J J, LI Q H, ZHU Z G. Vibratory localization of mistuned bladed disk assemblies—A review[J]. Advances in Mechanics, 2000, 30(4): 517-528 (in Chinese).
[22] CASTANIER M P, PIERRE C. Investigation of the combined effects of intentional and random mistuning on the forced response of bladed disks: AIAA-1998-3720[R]. Reston, VA: AIAA, 1998.
(责任编辑: 鲍亚平, 徐晓)
*Corresponding author. E-mail: aeroelastic@nwpu.edu.cn
Characteristics analysis of forced vibration response of mistuned cascades
ZHANG Weiwei1,*, GAO Yiqi1, QUAN Jinlou2, SU Dan1
1.NationalKeyLaboratoryofAerodynamicDesignandResearch,NorthwesternPolytechnicalUniversity,Xi’an710072,China2.AECCSichuanGasTurbineEstablishment,Chengdu610500,China
This paper employs a reduced order aerodynamic model based on Computational Fluid Dynamics (CFD), coupled with the structural dynamic equation, to analyze the forced vibration response of the mistuned cascade. The displacement amplitude of the typical transonic cascade in the tuned and mistuned cases are calculated by the proposed method, and the effect of mistuning patterns, mistuning strengths and mass ratios on the forced vibration response amplitude of the mistuned cascade are investigated quantitatively. The results show that the stiffness mistuning patterns in this paper can improve the stability of the cascade, but can also result in the increase of the modal localized level. The maximum vibration amplitude magnification factor has a peak value as the mistuning strength increases or the mass ratio decreases, and the peak value is significantly affected by mistuning patterns. Due to its efficiency in the analysis of the modal localization of the mistuned cascade with forced vibration, the proposed method is beneficial for engineering applications.
computational fluid dynamics (CFD); reduced order model (ROM); fluid-structrual coupling; mistuning; forced response
2016-12-05; Revised: 2017-01-01; Accepted: 2017-02-26; Published online: 2017-03-20 15:14
URL: www.cnki.net/kcms/detail/11.1929.V.20170320.1514.008.html
National Natural Science Foundation of China (11172237)
V211.47
A
1000-6893(2017)09-521018-10
2016-12-05; 退修日期: 2017-01-01; 录用日期: 2017-02-26; 网络出版时间: 2017-03-20 15:14
www.cnki.net/kcms/detail/11.1929.V.20170320.1514.008.html
国家自然科学基金 (11172237)
*通讯作者. E-mail: aeroelastic@nwpu.edu.cn
张伟伟, 高弈奇, 全金楼, 等. 失谐叶栅的受迫振动响应特性分析[J]. 航空学报, 2017, 38(9): 521018. ZHANG W W, GAO Y Q, QUAN J L, et al. Characteristics analysis of forced vibration response of mistuned cascades[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(9): 521018.
http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn
10.7527/S1000-6893.2017.621018

