空时分组编码的无人机中继通信航迹规划方法
刘海涛, 赵文强, 李春鸣, 李冬霞
中国民航大学 天津市智能信号与图像处理重点实验室, 天津 300300
空时分组编码的无人机中继通信航迹规划方法
刘海涛*, 赵文强, 李春鸣, 李冬霞
中国民航大学 天津市智能信号与图像处理重点实验室, 天津 300300
无人机(UAV)中继通信是实现远距离点对点无线通信的一种重要技术手段。为提高无人机中继通信系统链路传输的可靠性,提出基于空时分组编码的无人机放大转发中继通信传输方案,并基于双跳链路遍历容量最大化的准则给出了无人机最佳航迹规划方法,并进一步利用FM-EM算法给出了基于空时分组编码无人机中继通信系统的中断概率及遍历信道容量计算公式。计算机仿真表明:提出的方法显著优于传统的单发单收(SISO)无人机中继通信系统。
无人机中继; 航迹规划; 空时分组编码; FM-EM算法; 性能分析
相对于固定中继通信,无人机(UAV)中继通信具有通信距离远、部署方便、中继位置灵活可控、系统构建迅捷、维护成本低廉等诸多优点,因此无人机中继通信系统在军用与民用领域获得广泛的应用[1-2]。与此同时,由于无人机的高速机动性以及无人机能量受限等特性,无人机中继通信也带来一系列新问题[3-4],例如无人机中继网络拓扑结构快速变化,中继无人机的航迹规划等,因此针对无人机中继通信带来的特殊问题开展关键技术的研究具有重要的意义。
目前,无人机中继通信的研究主要集中在以下5个领域:无人机空地信道的建模[5-6]、无人机中继网络优化[7-9]、无人机中继通信传输方法[10-12]、无人机中继通信性能分析[13-15]、中继无人机的航迹规划[16-20]。围绕着中继通信无人机的航迹规划问题,相关研究如下:针对多用户接入的无人机中继通信系统的性能优化问题,文献[16]基于各态历经归一化传输速率最大化的准则给出了无人机航迹规划方法,然而在优化无人机航迹时仅考虑了用户节点-无人机的单跳链路,没有考虑无人机-基站链路对整体系统性能的影响。同样针对多用户接入的无人机中继通信最优化问题,文献[17]基于平均和速率最大化的准则及用户最小速率最大化的准则提出两种无人机航迹规划方法,然而该文章也仅考虑了用户节点-无人机单跳链路,没有考虑无人机-基站链路对性能的影响。针对无人机中继广播通信系统的航迹规划问题,文献[18]基于最小各态历经链路容量最大化的准则提出了一种低复杂度的无人机航迹规划方法,该方法主要特点是无需精确知晓各个用户的位置信息。针对点对点无人机中继通信的航迹规划问题,文献[19]提出基于发射波束成形与接收波束成形的无人机中继传输方法,并基于信噪比最大化的准则给出无人机航迹规划方法,然而该方法要求接入节点发射机与基站接收机均需精确知晓信道的衰落信息,实际应用中发射机难以获取信道的衰落信息,因此该方法应用于实际系统非常困难。
为提高点对点无人机中继通信系统链路传输的可靠性,同时降低无人机中继通信系统实现的复杂度,本文在文献[7]的基础上提出了基于空时分组编码的无人机放大转发中继传输方法,给出相应的无人机中继通信系统模型,以该模型为基础,推导给出无人机中继通信系统遍历容量计算公式,基于系统遍历容量最大化的准则给出了中继无人机的最佳航迹规划方法,并利用FM-EM(Finite Mixture-Expectation Maximum)算法给出了系统的中断概率与遍历容量计算公式,最后通过仿真验证了论文所提方法的正确性及有效性。本文存在3个方面的贡献:① 提出了基于空时分组编码(STBC)的无人机中继通信系统无人机航迹规划方法;② 理论分析给出所提出传输方法的中断概率及遍历容量计算公式;③ 证明了空时分组编码的无人机中继通信系统优于传统单发单收无人机中继传输方法。
1 空时分组编码的无人机中继系统模型
1.1 系统模型
图1给出了空时分组编码的无人机中继通信系统的模型。系统由可移动式接入节点(Access Point, AP)、高速运动的固定翼无人机及固定地面基站(Base Station, BS)组成。假设AP与BS的距离很远,系统不存在AP与BS之间的直达通信链路,为实现AP与BS节点间的相互通信,必须通过UAV中继来实现AP与BS之间的通信,为叙述方便,本文仅考虑AP至BS节点的通信。为提高UAV中继通信系统的链路传输可靠性,同时降低系统实现的复杂性,本文采用空时分组编码的UAV中继通信方案,AP采用两天线空时分组编码发射分集方式传输信号,UAV采用单天线放大转发协议中继信号,BS采用多天线最大比值合并(Maximal-Ratio Combining, MRC)方法合并信号以提高链路传输的可靠性。

图1 空时分组编码的无人机中继通信系统Fig.1 UAV relay communication system with space-time block coding
1.2 信号模型

(1)
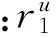
(2)


(3)
然后UAV以一定发射功率将信号转发至BS。在第3个时隙,BS两个接收天线(为叙述方便,BS使用两个接收天线,本方法容易推广到BS使用多个接收天线的场合)接收到的信号表示为
(4)
在第4个时隙,基站两个天线接收到的信号表示为
(5)

(6)

(7)
(8)
假设BS接收机通过信道估计可精确获得所有信道的衰落系数,则BS接收机进一步按式(9)给出方法对BS两个时隙接收到的信号进行相关合并处理:
(9)
将式(4)与式(5)分别代入式(9),化简后得到
(10)
式中:




(11)


(12)
进一步假设无人机的飞行高度始终保持为h,且无人机以恒定速度v飞行,则UAV在t时刻的位置可根据其t-Δt时刻位置信息,并利用以下方程更新获得[17,21]:
(13)
式中:δt为t时刻UAV的航向角,其满足δt-Δt-δmax≤δt≤δt-Δt+δmax,其中δmax为UAV的最大转弯角;Δt为UAV位置更新的时间间隔。将式(13)代入式(12),化简后得到
(14)
式(14)表明:在t-Δt时刻UAV的位置给定后,t时刻AP-UAV及UAV-BS的距离仅决定于t时刻UAV的航向角δt。
2 无人机航迹规划方法与性能分析
2.1 UAV最佳航迹规划方法
在无人机中继通信系统中,由于AP与UAV均处于运动状态,AP-UAV及UAV-BS的距离处于不断地变化中,为保证无人机中继通信系统链路传输可靠性最优,需要根据AP移动路径的变化优化UAV的飞行航迹。考虑到遍历容量是衡量无线通信系统链路传输可靠性的主要技术指标,因此论文基于系统遍历容量最大化准则来优化无人机的航迹。t时刻无人机中继通信系统的遍历容量表示为[22]

(15)
式中:由于直接对式(15)进行统计平均运算非常困难,论文利用泰勒级数的方法展开式(15),进一步考虑到展开式中高阶项的取值较小,且对高阶项进行统计平均运算的复杂度较高,因此仅保留展开式中的线性项得到

(16)
式中:E(rout,t)为t时刻接收机解调器输入的平均信噪比,其表达式为
(17)
考虑到式(17)计算仍比较困难,再次利用泰勒级数对式(17)展开,同理取展开式中的第1项,式(17)可简化为


(18)
根据式(18)可得出,影响t时刻UAV中继通信系统BS接收机解调器输入平均信噪比的影响因素为大尺度衰耗(dAU,t,dUB,t)。因此,将式(14)代入式(18),可观测得到以下结论:在t-Δt时刻UAV位置给定情况下,t时刻UAV中继通信系统BS接收机解调器输入平均信噪比仅决定于t时刻UAV的航向角δt。为使t时刻中继通信系统链路容量最大化,本文基于最大化遍历容量准则来优化UAV的航向角,以上优化准则可表述为
s.t. |δt-δt -Δt|≤δmax
(19)
此外进一步考虑到log2(·)为单调递增函数,因此式(19)的优化问题最后表述为
s.t. |δt-δt -Δt|≤δmax
(20)

2.2 性能分析
(21)
式中:b(opt)为b的最佳值。
2.2.1 系统的中断概率
中断概率是衡量无线通信系统链路传输可靠性的一项重要技术指标,其定义为接收信噪比低于某一门限值rth的概率[22],即
(22)


(23)

利用式(23)得到的t时刻BS接收机解调器输入瞬时信噪比的概率密度函数,式(22)可进一步化简为
(24)
式中:Q(η)为高斯Q函数,具体可表示为
(25)
2.2.2 系统的遍历容量
为了计算得到系统的遍历容量,本文首先通过FM-EM算法来估计得到t时刻系统遍历容量Ct的瞬时概率密度函数fCt(c),随后利用估计得到的概率密度函数fCt(c),可计算得到UAV中继系统的遍历容量为
(26)
3 数值仿真
3.1 仿真参数设置

3.2 仿真结果与分析
图2为UAV最佳航迹随着AP运动路线变化的曲线,图2横坐标与纵坐标分别代表直角坐标系的x轴与y轴,蓝色的曲线代表AP的运动路线,粉色曲线代表UAV的最佳航迹。曲线比较表明:① 当AP运动时,UAV通过调整其航向角使UAV跟随AP路径的变化飞行;② 当 UAV跟随AP运动飞行时,UAV的航迹呈现为圆形,原因为由于UAV的飞行速度大于AP的移动速度,且UAV飞行受到最大转弯角的限制,为了保证UAV中继通信系统的性能达到最佳,UAV在某些时刻必须以绕圆方式飞行。
图3给出了不同最大转弯角对UAV飞行航迹的影响(最大转弯角分别为10° 与15°),其中,黑色的曲线是最大转弯角为15° 时UAV最佳飞行航迹,粉色的曲线表示的是最大转弯角为10° 时UAV的最佳航迹。曲线比较表明:当最大转弯角取值较小时,无人机绕圆飞行的半径较大;当最大转弯角取值较大时,无人机绕圆飞行的半径较小。产生以上现象的原因是:无人机飞行速度给定情况下,最大转弯角的增大意味着无人机可选择最佳航向角的范围增大, 导致无人机绕圆飞行的半径变小。

图2 UAV最佳航迹随AP运动路线变化的曲线Fig.2 Optimal trajectories of UAV changing with the mobility of AP

图3 不同最大转弯角对UAV的飞行航迹的影响 Fig.3 Trajectories of UAV with different maximum heading
图4和图5分别给出了无人机中继通信系统的中断概率及遍历容量随时间变化的曲线。图4和图5包含两类曲线,标识为实线的曲线代表理论计算得到的曲线,标识为“o”型的曲线代表蒙特卡罗仿真得到的曲线;其中红色曲线代表的是采用空时分组编码的无人机中继系统的中断概率和遍历容量曲线,黑色曲线代表的是采用单发单收(Single-Input Single-Output, SISO)无人机中继系统的中断概率与遍历容量曲线。曲线比较表明:① 理论计算得到曲线与蒙特卡罗仿真得到的曲线完全一致,表明本文提出的航迹规划方法的正确性;② 本文提出的空时分组编码的无人机中继通信方案显著优于单发单收无人机中继通信系统方案,表明论文提出方法的有效性。

图4 中继系统中断概率随时间的变化曲线(δmax=10°) Fig.4 Outage probability of relay system vs time(δmax=10°)

图5 中继系统遍历容量随时间的变化曲线(δmax=10°) Fig.5 Ergodic capacity of relay system vs time(δmax=10°)
图6与图7分别显示最大转弯角对UAV中继通信系统中断概率及遍历容量性能的影响(最大转弯角分别为10° 与15°)。曲线比较表明:① 不同最大转弯角情况下,空时分组编码的无人机中继通信方案仍优于单发单收无人机中继通信方案;② UAV的最大转弯角对UAV中继通信系统中断概率及信道遍历容量的影响不大。

图6 最大转弯角对中继系统中断概率性能的影响 Fig.6 Outage probability of relay system withdifferent maximum turning angle

图7 最大转弯角对中继系统遍历容量性能的影响Fig.7 Ergodic capacity of relay system with different maximum turning angle
4 结 论
1) 本文提出了空时分组编码的无人机中继通信系统无人机最佳航迹规划方法。
2) 空时分组编码的无人机中继通信系统优于单发单收无人机中继通信系统。
3)无人机的最大转弯角对无人机中继通信系统的中断概率及遍历容量影响不大。
[1] FREW E W, BROWN T X. Airborne communication networks for small unmanned aircraft systems[J]. Proceedings of the IEEE, 2008, 96(12): 2008-2027.
[2] HAYAT S, YANMAZ E, MUZAFFAR R. Survey on unmanned aerial vehicle networks for civil applications: A communications viewpoint[J]. IEEE Communications Surveys & Tutorials, 2016, 18(4): 2624-2661.
[3] ZENG Y, ZHANG R, TENG J L. Wireless communications with unmanned aerial vehicles: Opportunities and challenges[J]. IEEE Communications Magazine, 2016, 54(5): 36-42.
[4] GUPTA L, JAIN R, VASZKUN G. Survey of important issues in UAV communication networks[J]. IEEE Communications Surveys & Tutorials, 2016, 18(2): 1123-1152.
[5] SIMUNEK M, FONTAN F P, PECHAC P. The UAV low elevation propagation channel in urban areas: Statistical analysis and time-series generator[J]. IEEE Transactions on Antennas and Propagation, 2013, 61(7): 3850-3858.
[6] MATOLAK D W, SUN R. Unmanned aircraft systems: Air-ground channel characterization for future applications[J]. IEEE Vehicular Technology Magazine, 2015, 10(2): 79-85.
[7] PALAT R C, ANNAMALAU A, REED J R. Cooperative relaying for ad-hoc ground networks using swarm UAVs[C]//2005 Military Communications Conference. Piscataway, NJ: IEEE Press, 2005: 1588-1594.
[8] HAN Z, SWINDLEHURST A L, LIU K. Optimization of MANET connectivity via smart deployment/movement of unmanned air vehicles[J]. IEEE Transactions on Vehicular Technology, 2009, 58(7): 3533-3546.
[9] 徐赞新, 袁坚, 王钺, 等. 一种支持移动自组网通信的多无人机中继网络[J]. 清华大学学报: 自然科学版, 2011, 51(2): 150-155.
XU Z X, YUAN J, WANG Y, et al. UAV relay network to provide communications in mobile ad hoc networks[J]. Journal of Tsinghua University: Science and Technology, 2011, 51(2): 150-155 (in Chinese).
[10] PALAT R C, ANNAMALAU A, REED J H. Cooperative relaying for ad-hoc ground networks using swarm UAVs[C]//2005 IEEE Military Communications Conference. Piscataway, NJ: IEEE Press, 2005: 1588-1594.
[11] CHENG C M, HSIAO P H, KUNG H T, et al. Maximizing throughput of UAV-relaying networks with the load-carry-and-deliver paradigm[C]//2007 IEEE Wireless Communications and Networking Conference. Piscataway, NJ: IEEE Press, 2007: 4417-4424.
[12] ONO F, OCHIAI H, MIURA R. A wireless relay network based on unmanned aircraft system with rate optimization[J]. IEEE Transactions on Wireless Communications, 2016, 15(11): 7699-7708.
[13] ABUALHAOL I Y, MATALGAH M M. Performance analysis of multi-carrier relay-based UAV network over fading channels[C]//2010 IEEE GLOBECOM Workshops. Piscataway, NJ: IEEE Press, 2010: 1811-1815.
[14] 欧阳键, 庄毅, 薛羽, 等. 非对称衰落信道下无人机中继传输方案及性能分析[J]. 航空学报, 2013, 34(1): 130-140.
OUYANG J, ZHUANG Y, XUE Y, et al. UAV relay transmission scheme and its performance analysis over asymmetric fading channels[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(1): 130-140 (in Chinese).
[15] 林敏, 魏恒, 欧阳键, 等. 无人飞行器中继双跳无线链路中的优化设计及性能分析[J]. 系统工程与电子技术, 2015, 37(6): 1391-1398 (in Chinese).
LIN M, WEI H, OUYANG J, et al. Optimal design and performance analysis for two-hop wireless links with UAV relaying[J]. Systems Engineering and Electronics, 2015, 37(6): 1391-1398 (in Chinese).
[16] ZHAN P, YU K, SWINDLEHURST A L. Wireless relay communications with unmanned aerial vehicles: Performance and optimization[J]. IEEE Transactions on Aerospace and Electronics Systems, 2011, 47(3): 2068-2085.
[17] FENG J, SWINDLEHURST A L. Optimization of UAV heading for the ground-to-air uplink[J]. IEEE Journal on Selected Areas in Communications, 2012, 30(5): 993-1005.
[18] CHOI D H, JUNG B H, DAN K S. Low-complexity maneuvering control of a UAV-based relay without location information of mobile ground nodes[C]//2014 IEEE Symposium on Computers and Communications (ISCC). Piscataway, NJ: IEEE Press, 2014: 1-6.
[19] OUYANG J, ZHUANG Y, LIN M, et al. Optimization of beamforming and path planning for UAV-assisted wireless relay networks[J]. Chinese Journal of Aeronautics, 2014, 27(2): 313-320.
[20] 符小卫, 程思敏, 高晓光. 无人机协同中继过程中的路径规划与通信优化[J]. 系统工程与电子技术, 2014, 36(5): 890-894.
FU X W, CHENG S M, GAO X G. Path planning and communication optimizing in multi-UAVs cooperative communication relay[J]. Systems Engineering and Electronics, 2014, 36(5): 890-894 (in Chinese).
[21] DUBINS L E. On curves of minimal length with a constraint on average curvature, and with prescribed initial and terminal positions and tangents[J]. American Journal of Mathematics, 1957, 79(3): 497-516.
[22] SIMON M K, ALOUINI M S. Digital communication over fading channels[M]. 2nd ed. Hoboken, NJ: John Wiley and Sons, Inc., 2005: 20-24.
[23] ZAIDI Z R, MARK B L, THOMAS R K. A two-tier representation of node mobility in ad hoc networks[C]//2004 First IEEE Communications Society Conference on Sensor and Ad Hoc Communications and Networks. Piscataway, NJ: IEEE Press, 2004: 153-161.
[24] MCLACHLAN G, PEEL D. Finite mixture models[M]. New York: Wiley, 2000: 47-50.
附录A: FM-EM算法
假设在FM模型中,被估计的概率密度函数fZ(z)由N个高斯分布的概率密度函数加权求和组成。因此对于单变量的FM模型,随机变量Z的概率密度函数可表示为[24]

(A1)
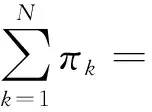
(A2)
对于上述FM模型中混合项的参数的估计可利用经典算法——EM算法。利用EM算法估计FM模型中混合项的参数,首先,①要确定混合项的个数N;②被估计参数的初始值Θ0;③ EM算法迭代的终止条件ε。其次,可利用EM算法的迭代公式不断更新这些参数值直到满足EM算法的终止条件。下面将给出上述参数的具体迭代公式:
(A3)

k=1,2,…,N;p=1,2,…,M
(A4)
(A5)
再根据式(A3)对μk求偏导数可得μk的更新公式为
(A6)
(A7)
现在把应用EM算法进行FM模型估计的实施步骤归纳如下:
步骤1 确定FM模型中混合项的项数N。
步骤3 利用式(A4)计算每一个观测数据zp所对应的后验概率。
步骤4 利用式(A5)~式(A7)更新参数集Θ。
步骤5 重复第3步与第4步直到EM算法收敛。
附录B: AP运动模型
AP运动模型采用一阶自回归模型[23]。假定AP在t-Δt时刻的状态用sA,t-Δt表示,即

(B1)

sA,t=TAsA,t -Δt+wA,t
(B2)
(B3)

(责任编辑: 苏磊)
*Corresponding author. E-mail: hitliucauc@qq.com
Path planning method for UAV relay communication system with space-time block coding
LIU Haitao*, ZHAO Wenqiang, LI Chunming, LI Dongxia
TianjinKeyLaboratoryforAdvancedSignalProcessing,CivilAviationUniversityofChina,Tianjin300300,China
Unmanned Aerial Vehicle (UAV) relay communication is an important technical scheme for long range point-to-point wireless communications. To improve the reliability of transmission link for the UAV relay communication system, a novel UAV relay transmission scheme is proposed based on space-time block coding. According to the criterion of maximizing the average mutual information of the dual-hop link of the UAV relaying communication system, an optimal path planning method for the UAV relay communication system is presented. The outage probability and ergodic capacity of the UAV relay communication system are derived using Finite-Mixture with Expectation-Maximization (FM-EM) algorithm. The computer simulation results indicate that the proposed scheme is superior to the traditional Single-Input Single-Output (SISO) UAV relay communication scheme.
Unmanned Aerial Vehicle (UAV) relay; path planning; space-time block coding; FM-EM algorithm; performance analysis
2016-12-13; Revised: 2017-03-10; Accepted: 2017-03-25; Published online: 2017-04-11 10:21
URL: www.cnki.net/kcms/detail/11.1929.V.20170411.1021.004.html
National Key Research and Development Plan (2016YFB0502402)
2016-12-13; 退修日期: 2017-03-10; 录用日期: 2017-03-25; 网络出版时间: 2017-04-11 10:21
www.cnki.net/kcms/detail/11.1929.V.20170411.1021.004.html
国家重点研发计划(2016YFB0502402)
*通讯作者.E-mail: hitliucauc@qq.com
刘海涛, 赵文强, 李春鸣, 等. 空时分组编码的无人机中继通信航迹规划方法[J]. 航空学报, 2017, 38(9): 321048. LIU H T, ZHAO W Q, LI C M, et al. Path planning method for UAV relay communication system with space-time block coding[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(9): 321048.
http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn
10.7527/S1000-6893.2017.321048

