平台式惯性导航系统在线可靠性评估技术
钱超, 张子剑, 李大伟
1.海军工程大学 科研部, 武汉 430033 2.中国船舶重工集团公司第707研究所, 天津 300131 3.中国人民解放军91550部队, 大连 116023
平台式惯性导航系统在线可靠性评估技术
钱超1, 张子剑2, 李大伟3,*
1.海军工程大学 科研部, 武汉 430033 2.中国船舶重工集团公司第707研究所, 天津 300131 3.中国人民解放军91550部队, 大连 116023
平台式惯性导航系统是现代导航的重要设备,由于其所处环境和制造工艺各不相同,导致各个体之间的可靠性有着明显的差异。如果对收集到的性能误差数据进行统一处理,无法准确地反映个体之间的差异性,不利于掌握平台式惯性导航系统个体的可靠性规律。针对该问题,对平台式惯性导航系统的在线可靠性评估方法进行了重点研究。结合平台式惯性导航系统使用过程中的性能变化特点和失效机理,利用复合Poisson过程建立了其性能退化模型,并给出了性能参数评估方法。通过算例分析,说明建立的性能退化模型能够较好地描述平台式惯性导航系统的性能退化规律,有助于掌握平台式惯性导航系统的可靠性水平。
在线可靠性; 性能退化; 复合Poisson过程; 可靠性评估; 平台式惯性导航系统
平台式惯性导航系统属于典型的高可靠、长寿命设备,由于不同批次设备的制造工艺以及使用环境不同,导致了各个体之间的可靠性水平差异性较大。如果对不同批次的设备进行统一处理,其结果反映的是平台式惯性导航系统(以下简称为平台惯导)整体的可靠性水平。对于使用者而言,往往更关心系统的个体可靠性,希望实时了解系统的导航精度,以便为舰船导航、武器系统使用提供重要的信息。由此可见,开展平台惯导在线可靠性研究具有重要的实用意义[1-2]。
平台惯导使用过程中,性能误差量会随着工作时间的延长而逐渐变化,当超过失效阈值时便认为失效。通过处理收集到的性能退化量信息,可以实时描述平台式惯性系统的性能变化规律,进而掌握其在线可靠性水平。近年来,国内外学者利用退化轨迹法、图分析法和随机过程法等方法[3-4]对性能退化信息进行了处理,开展了各类产品的在线可靠性评估研究,比如文献[5]利用随机过程方法建立了产品的退化模型,并基于Bayes方法对产品的实时可靠性进行了估计;文献[6]利用图分析法对退化量分布进行拟合,并给出了相应参数的估计方法,进而实时预测电子产品的可靠度。上述方法主要是针对检测不影响性能退化规律的基础上开展的研究,但是对于平台惯导而言,由于其使用的特殊性,为了保证使用精度,通常会进行初始对准和综校[7-8],表现为定期恢复系统的性能退化量。显然,平台惯导的性能退化规律会因此受到一定的影响,如果直接利用上述方法无法准确地描述其使用过程中的性能退化规律,进而不利于掌握其在线可靠性水平。
论文针对平台惯导,在获取其在线误差数据后,重点研究了其在线可靠性评估。通过分析平台惯导使用过程中性能变化特点,结合失效机理,在充分考虑初始对准和综校影响下,建立了其性能退化规律模型,并给出了性能参数的极大似然估计。通过数值分析,并与工程经验比较,证明方法的可行性。
1 系统性能变化特点分析
平台惯导由大量的机械零件和电子元器件组成。随着时间的延长,平台惯导使用过程中,由于温、湿度等外界因素的作用而引起元器件发生老化,出现误差。同时,因为陀螺自身漂移的影响,也会造成测量值偏离真值,产生误差。
为了保证平台惯导的使用精度,每次使用前会进行初始对准,消除部分性能误差值。同时,在使用过程中又会定期进行综校,对因陀螺仪漂移产生的性能误差进行补偿和消除。由于综校对误差的补偿效果较为有限,仅能恢复部分误差。因此,根据其使用要求,可以得到平台惯导的性能误差值X(t)随工作时间的变化情况如图1所示。图中Ls为误差允许最大值;t为工作时间。通过图1,可以发现性能误差值会随着时间延长逐渐增加。但是由于综校和初始对准具有恢复作用,导致性能误差值呈现出间断性的变化。同时,性能误差值早期变化幅度较小,趋于平缓,可是当工作到某一时刻后,便会突然变大,出现变化幅度较大的现象。由此可见,对于平台惯导而言,由于综校和初始对准的影响,导致其性能变化具有间断性和突变性2个特点。
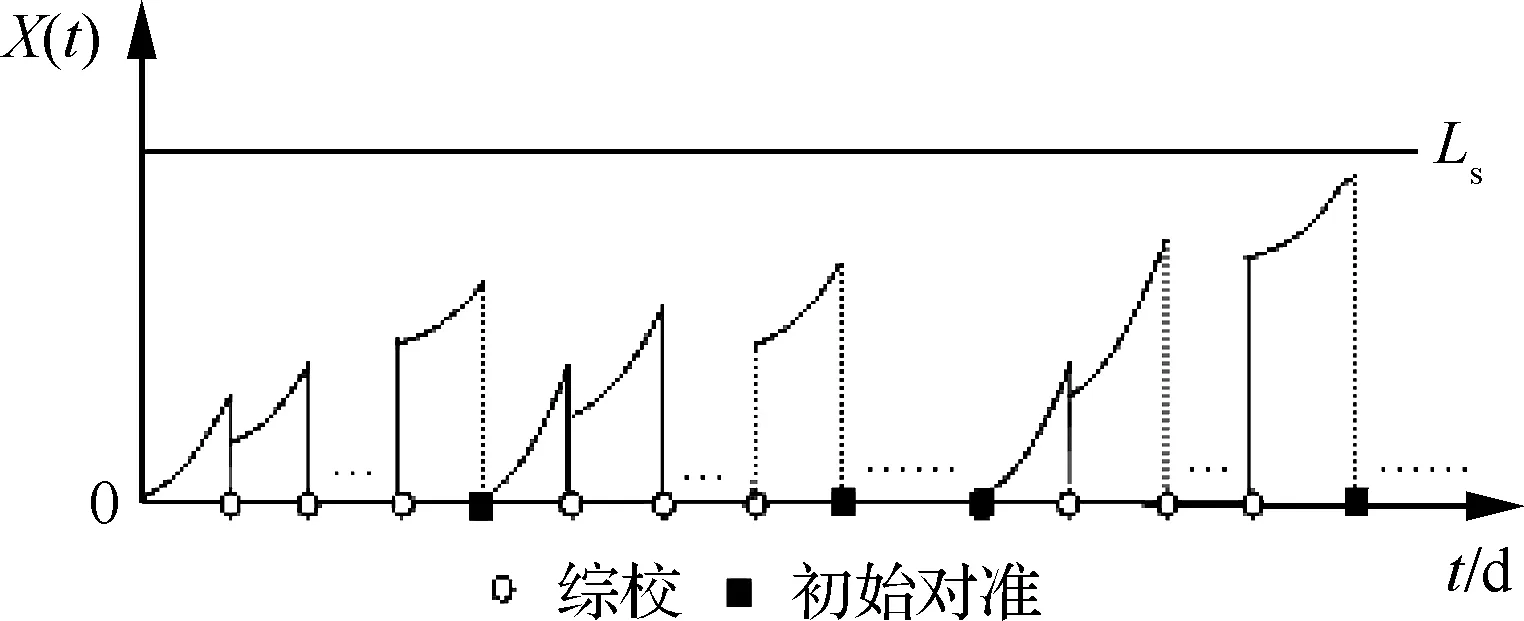
图1 性能变化示意图Fig.1 Schematic diagram of performance change
2 系统性能退化规律建模
2.1 基础模型
随着材料学、失效物理分析等相关技术的发展,部分产品的性能退化可以由累积失效模型进行解释[9-11]。表现为产品使用过程中会受到振动、温度等外界因素的影响,引起自身性能状态发生变化,变化量会逐渐的累积,当超过某一阈值时变化发生失效。平台惯导属于典型的机电一体设备,其由陀螺仪、电机和电源等部件组成。因此,可以认为平台惯导部分性能误差是由自身性能退化引起的。
根据累积失效模型,需要对平台惯导的外界作用规律和自身变化规律进行描述,因此,作出以下假设:
1) 假设系统在时间[t,t+s]内受到外界因素的作用数Nt,t+s服从强度函数为a1b1tb1-1的非齐次Poisson过程[12],即
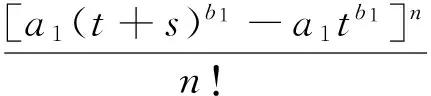
exp{-[a1(t+s)b1-a1tb1]}n=1,2,…
(1)
式中:a1和b1为性能参数。
2) 外界因素每次作用会对系统的性能造成一定影响,影响程度一般与其材料、制造工艺等质量属性有关,所以假设每次作用对系统造成的性能变化量Yi相互独立且服从相同的正态分布,即

3) 由于Nt,t+s、Yi分别与系统工作坏境、自身属性有关,一般假设两者互相独立[13]。
利用上述假设,可以确定平台式惯性导航在时间[t,t+s]内的性能退化量Xt,t+s为在该时间段内受到的作用数Nt,t+s与每次作用造成的性能变化量Yi的累加和,具体的表达式为
(2)
显然,Xt,t+s为一个典型的复合Poisson过程。
根据式(2),可以确定系统在[t,t+s]时间内的性能退化量Xt,t+s为Nt,t+s个正态分布的线性组合,即
(3)
由于外界作用数Nt,t+s和每次作用后的性能变化量Yi都为随机变量,导致式(3)的解析表达式较为复杂。
根据复合Poisson过程的性质,可以确定在[t,t+s]时间内的性能退化量Xt,t+s的数学期望和方差分别为
(4)
通过式(3)可以确定性能退化量Xt,t+s为无穷个互相独立的变量累加和,根据中心极限定理可以认为Xt,t+s近似服从正态分布,即
(5)

通过分析,明确陀螺仪自身漂移同样会造成一定的性能误差。一般情况,可以假设平台惯导任意时刻t因陀螺仪漂移引起的性能退化量X1(t)服从正态分布,具体形式为
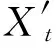
(6)


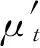
式中:m′为因陀螺仪确定性漂移引起的变化均值单位时间内的变化值;n′为因陀螺仪随机性漂移引起的变化方差单位时间内的变化值。由上式可知,均值和方差是时间的函数且随时间的延长呈指数幂变化。特别地,当a2=b2=1时,可以认为均值和方差随时间延长线性增加。
2.2 基于综校和初始对准的性能退化模型

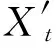
(7)

实际中,产品性能退化往往是不可逆的过程。对于平台惯导而言,因性能退化产生的误差很难通过技术手段进行彻底消除。因此,可以认为初始对准仅是对累积退化量进行恢复,并不会影响外界作用规律。结合式(5),记初始对准时刻分别为T1,T2,…,Tj,得到平台惯导任意时刻t因自身性能退化引起的性能退化量Xt不超过x的概率满足
P(Xt≤x)=
(8)
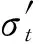
综上所示,平台惯导的性能退化量主要由两部分引起:自身性能退化和陀螺仪漂移,由于两者的作用机理不同,可以认为两部分互相独立,结合正态分布的可加性,根据2.1节分析,得到平台惯导任意时刻t的性能退化量X(t)不超过y的概率满足
(9)
式中:t∈(Tj+iΔt,Tj+(i+1)Δt],Tj+(i+1)·Δt 进一步分析,在得到平台惯导的性能退化规律式(9)后,已知最大允许误差Ls,在给定初始对准时刻和综校周期后,建立其性能可靠性模型为 R(t)=P(X(t) (10) 式中:kl=[Tl/Δt],表示第l个周期内综校次数。由式(10)可知,平台惯导的可靠度不仅与工作时间t有关,而且还与每次初始对准时刻有着密切的关系,而一般产品仅与工作时间有关。 对于平台惯导而言,通常可以收集到单台系统每次使用过后的性能退化数据,表现为时刻ti的性能退化值为yi(i=1,2,…,j)。进一步分析,由于综校能够有效地对平台惯导因陀螺仪漂移引起的性能误差进行补偿,并且工程中综校周期相对较短,所以因陀螺仪漂移引起的性能误差相对较小。同时,由于实际中收集到的性能退化数据为两类误差之和,无法区分误差的具体数值,所以在处理过程中可将参数进行合并处理,结合式(9),利用数值近似,将平台惯导的性能退化规律近似为式(11)。 (11) 式中:g和h分别为平台惯导单位时间内的均值和方差变化值;w为平台惯导退化和陀螺仪漂移产生误差随时间增加的强度。 因此,只要确定参数g、h和w便可以掌握平台惯导的在线性能可靠性规律。利用收集到得的性能误差值yi,构造似然函数并化简可得 L(g,h,w|(t1,y1),(t2,y2),…,(tj,yj))∝ (12) 对式(12)两端取对数并分别对参数g、h和w求导,令求导后的式子分别为零,整理后得到如下方程组: (13) X(t2) (14) 式中:t∈(tj-1,tj]。 通过跟踪某平台惯导,能够获得其航向精度误差数据。已知其工作时间分别为180、360、540、720、900和1 080 d,综校周期为24 h,获得的航向精度误差数据如表1所示。 如表1所示,误差数据并不是单调增加。这 表1 航向精度误差数据Table 1 Error data of course accuracy 是因为每次初始对准都会将误差值恢复到零值,下一个工作周期,平台惯导的航向精度偏差将从零值开始变化,出现间断性,所以误差数据不再单调变化。同时,由于外界作用和作用后性能变化量的随机性,导致收集到的性能误差数据出现“倒挂”现象,即前一个工作周期的误差会大于后一个工作周期。这恰恰反映了系统个体之间的差异性[14],如果将不同个体的数据进行平均处理,无法描述上述规律,造成很难掌握单个系统的可靠性规律。 经典方法因为不考虑初始对准对误差数据消除的影响,如果利用其进行处理,会将表1中的数据进行累加。因此,已知航向精度最大允许误差为6,累加后可以发现系统在360 d的误差为 8.88>6,表明系统在360 d便已经失效。而实际中,平台惯导的实际寿命远远大于360 d,与经验明显不符。由此可见,利用经典方法无法准确客观地评估平台惯导的在线可靠性。 统计该平台惯导同一批次的其他平台惯导失效数据,并结合工程经验,开展大量数值仿真,整理获得该平台惯导的可靠度真实值,将其与本文获得的可靠度估计值进行对比,具体效果如图2所示。 如图2所示,2条曲线较为接近,说明利用本文方法可以较好地描述惯性导航系统的在线可靠性规律。 进一步分析,可以发现平台惯导的可靠度呈现出阶梯状下降。这是因为初始对准的恢复作用延缓了可靠度下降速度,表现为每次工作早期系统基本不会失效。同时,可以发现系统可靠度为0.9时的可靠寿命为4.49 a,而可靠度为0.8时的可靠寿命为5.45 a,二者相差仅1 a,可见该时间段系统的可靠度变化较为剧烈,具体表现为性能误差值变化较为剧烈,引起系统失效。由此可见,本文方法可以较好地反映平台惯导的性能变化特点。 图2 可靠度对比图Fig.2 Comparison of reliability 为了进一步分析平台惯导的在线可靠性规律,利用本文方法按照上述处理步骤,得到不同批次生产的平台惯导可靠度变化规律,如图3所示。 图3 可靠度规律Fig.3 Rule of reliability 如图3所示,分析得到另一批次的平台惯导可靠度为0.9时的可靠寿命为6 a,可靠度为0.8时的可靠寿命为6.5 a。对比上一台系统,发现2个批次生产的平台惯导可靠性水平差异性较大。由此可见,需要开展平台惯导的在线可靠性研究,以便实时掌握单个系统的可靠性规律。 1) 通过开展平台惯导的在线可靠性评估研究,一方面建立了系统在综校和初始对准情况下的性能退化规律模型,描述了其使用过程的性能退化规律。 2) 另一方面,依据能够收集到的性能误差数据,对模型参数进行了估计分析,以便掌握系统的在线可靠性规律。 3) 算例分析表明,本文方法可以掌握平台式惯性导航的在线可靠性水平,为后期开展延寿、维修策略分析等研究奠定了理论基础。 [1] 郑梓祯, 刘德耀, 蔡迎波, 等. 船用惯性导航系统海上试验[M]. 北京: 国防工业出版社, 2006: 57-79. ZHENG Z Z, LIU D Y, CAI Y B, et al. Sea experiment for marine inertial navigation system[M]. Beijing: National Defense Industry Press, 2006: 57-79 (in Chinese). [2] 于化鹏, 吴文启, 周成, 等. 恒速偏频激光陀螺系统静基座初始对准中等效东向陀螺漂移估计[J]. 中国惯性技术学报, 2012, 20(3): 262-265. YU H P, WU W Q, ZHOU C, et al. Equivalent east gyro drift estimation in initial alignment for triad constant-rate biased RLG system on stationary base[J]. Journal of Chinese Inertial Technology, 2012, 20(3): 262-265 (in Chinese). [3] ZHANG C H, LU X, TAN Y Y, et al. Reliability demonstration methodology for products with Gamma process by optimal accelerated degradation testing[J]. Reliability Engineering and System Safety, 2015, 142(3): 369-377. [4] WANG X. Wiener processes with random effects for degradation data[J]. Journal of Multivariate Analysis, 2010, 101(2): 340-351. [5] WANG X L, JIANG P, GUO B, et al. Real-time reliability evaluation based on damaged measurement degradation data[J]. Journal of Central South University, 2012, 19(11): 3162-3169. [6] XU Z G, JI Y D, ZHOU D H. Real-time reliability prediction for a dynamic system based on the hidden degradation process identification[J]. IEEE Transactions on Reliability, 2008, 57(2): 230-242. [7] 何虔恩, 高钟毓, 吴秋平, 等. 基于互补滤波的惯导系统水平阻尼网络设计[J]. 中国惯性技术学报, 2012, 20(2): 157-161. HE Q E, GAO Z Y, WU Q P, et al. Design of horizontal damping network for INS based on complementary filtering[J]. Chinese Inertial Technology, 2012, 20(2): 157-161 (in Chinese). [8] 王东升, 张海峰, 张园园, 等. 平台式惯导系统方位调制的转速优化[J]. 中国惯性技术学报, 2013, 21(3): 312-317. WANG D S, ZHANG H F, ZHANG Y Y, et al. Azimuth modulation rotating speed optimization of platform inertial navigation system[J]. Journal of Chinese Inertial Technology, 2013, 21(3): 312-317 (in Chinese). [9] 张子剑, 钟强晖, 张志华. 退化产品可靠性评估方法的研究[J]. 中国惯性技术学报, 2007, 15(6): 752-755. ZHANG Z J, ZHONG Q H, ZHANG Z H. Evaluation method of degradation products’ reliability[J]. Journal of Chinese Inertial Technology, 2007, 15(6): 752-755 (in Chinese). [10] 曾声奎. 可靠性设计与分析[M]. 北京: 国防工业出版社, 2011: 81-98. ZENG S K. Reliability design and analysis[M]. Beijing: National Defense Industry Press, 2011: 81-98 (in Chinese). [11] MITRA F, ANTOINE G, LAURENCE D. On the use of on-line detection for maintenance of gradually deteriorating systems[J]. Reliability Engineering and System Safety, 2008, 93(12): 1814-1820. [12] PENG R, LI Y F, ZHANG W J, et al. Testing effort dependent software reliability model for imperfect debugging process considering both detection and correction[J]. Reliability Engineering and System Safety, 2014, 126(2): 37-43. [13] 李大伟, 张志华, 钟强晖, 等. 复杂退化系统的组合维修策略优化[J]. 航空学报, 2015, 36(3): 872-880. LI D W, ZHANG Z H, ZHONG Q H, et al. Optimal combination maintenance strategy of deteriorating complex system[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(3): 872-880 (in Chinese). [14] FAN M, HAN Q S, YANG X K. Energy minimization for on-line real-time scheduling with reliability awareness[J]. Journal of System and Software, 2017, 127: 168-176. (责任编辑: 张晗) *Corresponding author. E-mail: zeroing2009@163.com On-line reliability assessment of platform inertial navigation system QIAN Chao1, ZHANG Zijian2, LI Dawei3,* 1.OfficeofResearch&Development,NavalUniversityofEngineering,Wuhan430033,China2.No.707ResearchInstituteofChinaShipbuildingIndustryCorporation,Tianjin300131,China3.TroopNo.91550ofPLA,Dalian116023,China Platform inertial navigation system is important equipment of modern navigation. Because of variable environments and different manufacture levels, there is a distinct discrepancy between individual platform inertial navigation. Analysis of the collected performance deterioration data as a whole cannot reflect the individual discrepancy. To address this problem, on-line reliability assessment of platform inertial navigation system is investigated. Using composite Poisson process, a deterioration model is established based on the deterioration characteristics and failure mechanism of the platform inertial navigation system. The method for parameter estimation is given. Computation analysis of samples shows that the model can describe the performance deterioration law of the platform inertial navigation system, and is thus helpful for knowing the reliability level of the platform inertial navigation system. on-line reliability; performance deterioration; composite Poisson process; reliability assessment; platform inertial navigation system 2017-03-20; Revised: 2017-04-17; Accepted: 2017-05-22; Published online: 2017-06-02 16:55 URL: www.cnki.net/kcms/detail/11.1929.V.20170602.1655.010.html National Defence Pre-research Foundation (41404060101) V240.2; U666.1 A 1000-6893(2017)09-321259-07 2017-03-20; 退修日期: 2017-04-17; 录用日期: 2017-05-22; 网络出版时间: 2017-06-02 16:55 www.cnki.net/kcms/detail/11.1929.V.20170602.1655.010.html 国防预研基金资助项目(41404060101) *通讯作者.E-mail: zeroing2009@163.com 钱超, 张子剑, 李大伟. 平台式惯性导航系统在线可靠性评估技术[J]. 航空学报, 2017, 38(9): 321259. QIAN C, ZHANG Z J, LI D W. On-line reliability assessment of platform inertial navigation system[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(9): 321259. http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn 10.7527/S1000-6893.2017.3211593 在线可靠性评估

4 算例分析



5 结 论

