Aerodynamic multi-objective integrated optimization based on principal component analysis

Jingto HUANG,Zhu ZHOU,Zhenghong GAO,Mio ZHANG,Lei YU

aComputational Aerodynamics Institute,China Aerodynamics Research and Development Center,Mianyang 621000,China

bNational Key Laboratory of Aerodynamic Design and Research,Northwestern Polytechnical University,Xi’an 710072,China

cShanghai Aircraft Design and Research Institute,Commercial Aircraft Corporation of China Ltd.,Shanghai 201210,China

Aerodynamic multi-objective integrated optimization based on principal component analysis

Jiangtao HUANGa,*,Zhu ZHOUa,Zhenghong GAOb,Miao ZHANGc,Lei YUa

aComputational Aerodynamics Institute,China Aerodynamics Research and Development Center,Mianyang 621000,China

bNational Key Laboratory of Aerodynamic Design and Research,Northwestern Polytechnical University,Xi’an 710072,China

cShanghai Aircraft Design and Research Institute,Commercial Aircraft Corporation of China Ltd.,Shanghai 201210,China

Based on improved multi-objective particle swarm optimization(MOPSO)algorithm with principal component analysis(PCA)methodology,an efficient high-dimension multiobjective optimization method is proposed,which,as the purpose of this paper,aims to improve the convergence of Pareto front in multi-objective optimization design.The mathematical efficiency,the physical reasonableness and the reliability in dealing with redundant objectives of PCA are verified by typical DTLZ5 test function and multi-objective correlation analysis of supercritical airfoil,and the proposed method is integrated into aircraft multi-disciplinary design(AMDEsign)platform,which contains aerodynamics,stealth and structure weight analysis and optimization module.Then the proposed method is used for the multi-point integrated aerodynamic optimization of a wide-body passenger aircraft,in which the redundant objectives identified by PCA are transformed to optimization constraints,and several design methods are compared.The design results illustrate that the strategy used in this paper is sufficient and multi-point design requirements of the passenger aircraft are reached.The visualization level of non-dominant Pareto set is improved by effectively reducing the dimension without losing the primary feature of the problem.

©2017 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.This is an open access article under the CC BY-NC-NDlicense(http://creativecommons.org/licenses/by-nc-nd/4.0/).

1.Introduction

Multi-objective design methods mainly include weighted average optimization and non-dominated optimization based on Pareto idea.The former is actually a single point optimization method,and the design results strongly depend on the choice of weight function.Its main deficiency is that the selection of reasonable weight function is becoming more and more difficult with the increasing number of object.Improper weight may lose some important information as the design problem is going to be more complex.As a consequence,numerical optimization based on Pareto idea has played an important role in multi-disciplinary and multi-objective design of aircraft.However,the research mainly focuses on low dimensional multi-objective problems with simple shape and single design point.The application of Pareto in high dimensional optimization has several major problems1–3:

(1)The Pareto front would advance extremely slowly and is not reliable.With the increasing number of object(when≥3,in the following,it is named as multi-objective problem),the dimension of Pareto optimal front surface increases,and the number of point in the Pareto fronts would rise exponentially,which makes the time consumption and space complexity of the algorithm deteriorate greatly.

(2)The number of the non-dominated solution will grow dramatically.When the object reaches to a certain number,almost all individuals are non-dominated solutions,which will lead to serious weakening of performance based on Pareto dominance ranking and selection.For a given external group with fixed size,excellent individuals may not be preserved in the evolutionary process,making the entire algorithm search become slow and difficult to reach a reasonable Pareto front.So,the traditional optimization method is powerless in dealing with multi-objective problems.

(3)Wide design space and huge grid scale of complex configuration result in large computation expense and requirement of high population diversity.

(4)For designers,the visualization level of non-dominated solution set is not sufficient,which leads to a difficulty to make reasonable decisions.So,the traditional optimization method is powerless in dealing with multiobjective problems.

Aerodynamic design of wide-body aircraft is a typical multipoint integrated design process,in which the multiple design requirements such as the cruise lift-to-drag ratio,the buffer boundary and the drag divergence characteristic should be considered.At the same time, wide-body aircraft often use the crane wing-mounted engine con figuration.For this type of con figuration,the existence of pylon and nacelle will affect the pressure distribution of supercritical wing to a certain extent by a positive correlation with the sweep angle of wing, which may change some crucial aerodynamic characteristics.Therefore,for the fine design of wing-mounted engine con figuration,in fluence of pylon/nacelle on the wing must be considered.In addition,in order to maintain excellent aerodynamic performance after trimming the pitch moment,it is necessary to carry out integrated design considering the nacelle interference and the horizontal tail trimming.With the rapid development of computer,it is possible to conduct multi-objective and re fine integrated design for full aircraft con figuration,which,however,has not been deeply investigated in industrial field at present.

According to the above problems,in the large scale distributed parallel computing environment,multi-objective aerodynamic integrated design for wing,fuselage,pylon,nacelle,horizontal and vertical wing on cruise con figuration of wide body aircraft is studied based on improved multi-objective particle swarm optimization(MOPSO)algorithm coupling with principal component analysis(PCA)method.Validity of the design method in this paper is verified and the optimized results are discussed.

2.PCA-MOPSO optimization platform

2.1.Redundant object identification and dimensional reduction

The search process of Pareto-based algorithm slows down dramatically in multi-objective optimization,and the visualization level of non-dominated solutions is not conducive to make decision for designers.In data analysis,the data with less variables and more information is always expected.Actually,there is always a certain correlation between the variables in practice,and when there is a correlation between two variables,it can be explained that the information reflected by these two variables has a certain overlap,and then the dimension reduction can be achieved.PCA4,5has been widely accepted in image processing and data reduction because ofits ability of correlation analysis,variable identification,target recognition and the abnormal value grouping.6–8However,the application of PCA in aerodynamic multi-objective optimization is still rare.PCA method can identify the principal components as well as ‘redundant components” or ”sub components‘.Using the analysis results,we can regard ”sub components‘‘as a constraint or redundancy for the further dimension reduction.Based on the PCA method,the dimension reduction of multi-objective optimization can be realized by the following steps9,10:

Step 1 Initialize the iteration counterI=0,the target setM=∅,and the threshold TC.

Step 2 Initialize population randomly,and optimize to obtain a set of Pareto solutionP.

Step 3 Perform principal component analysis on the Pareto solutionP,and the redundant target can be eliminated by the specified threshold TC.The specific implementation strategies are as follows:

(A) Normalize the target vector to calculate the correlation matrix R(I,J)and the eigenvector V(I,J),and extract the first and second principal components via PCA analysis.

(B) For the first vector,select two targets with the most positive and negative elements into the setM;if all the elements have the same sign,select two corresponding targets with the maximum absolute value.

(C) For next component,check the threshold.If the threshold is met,end the cycle;otherwise,if the eigenvalue＜0.1,select corresponding target with the largest absolute value|max(V(I,J))|into theM.Otherwise.

(a) Select two corresponding objects with the most positive and negative elements into the setM.

(b) If all the elements have the same sign,select two corresponding targets with the maximum absolute value into the setM.

Step 4 IfM=M(I–1),stop and output the optimal solutions;otherwise,I=I+1 and return to Step 2.

After PCA analysis,we can identify the relationship between the targets so as to extract the principal target from the high dimensional object space and eliminate the redundant objects.The original design problem can be simplified without losing the main feature,and it would be beneficial for further decision-making.

2.2.Improved Pareto solver

Multi-objective particle swarm optimization(MOPSO)algorithm11was used.

where XpBest,XgBest,X,V are the individual best,the global best,current position and the update speed,ωaretherandom number,self learning factor,social learning factor and the inertia factor.In order to improve the convergence speed of MOPSO algorithm,7,8serial improvement was adopted:

(1)For the learning factors of particle swarm optimization(PSO)algorithm,the evolutionary direction enhancement function is introduced to accelerate the advancement of Pareto front.The learning factor in traditional particle swarm algorithm is constant in each dimension.In fact,however,the contribution of each dimension of design variables to the objective function is different.

If XgBestbetween the most adjacent generations changes,it will be denoted asAccording to these information,the learning factors of global and Pareto center can be modified.In order to reflect the contribution of different design variables to the objective function,the new learning factoris no longer a constant but a vector c'=The learning factor of any dimension can be modified as

where iter,Genmax,δ andNare the current generation,total generation,constant and design variable dimension respectively.

(2)Numerical experiments show that the treatment of particles over the boundary can directly affect the global performance and convergence of the multi-objective optimization algorithm.To decrease the probability of particle falling into local optimum on boundary,and accelerate the convergence of the algorithm in the latter stages,cross-border processing methods were also corrected by correction factor:

wherexi,maxandxi,minare the upper and lower bounds of design variables,randiis a random number,and the exponential term is the transition function.Different from the standard algorithm,the improved algorithm introduces the learning options for other information:

(3)If two adjacent generations of particles do not dominate each other,updating the best location or not will be determined by the probability,which would influence the front advanced velocity.The improved probability function was used as follows:

where Gen is the current evolutionary generation.The selection probability in the initial stage is bigger,which can enhance the diversity in the optimization process,and will reduce step by step in evolution.In the terminal stage,the selection probability will be relatively small in order to reduce the randomness of non-dominated solutions and accelerate Pareto front advancing.

2.3.PCA-MOPSO algorithm test

2.3.1.DTLZ5 test function

The DTLZ5 test function is designed by Khare et al.12,and is generally used to verify the performance of dimension reduction algorithm in multi-objective optimization.Its expression is as follows:

where

There is redundancy relationship between targets of DTLZ5 test function,which can be used to verify the performance of dimension reduction algorithm.For general test problems DTLZ5(I,M),Mrepresents the number of targets,andIrepresents the dimension of Pareto front.Under this definition,DTLZ5(3,5)is considered as a test example in this paper,in which the first two objective functions are redundant.The analytic Pareto front of DTLZ5(3,5)is a hyper sphere=1(Fig.1).

The optimal population size is 60 and the number of generation is 60.Fig.2 shows the Pareto front off3,f4andf5without dimension reduction,and it can be seen that with the increase of target dimension,the solution set of the Pareto front obviously deviates from the analytical solution.Then the Latin hypercube design and principal component analysis are carried out.Table 1 shows the analysis results,and the pro-portion of each component contribution is given in Table 2,TC is threshold value.It can be seen thatf2andf1are the ‘redundant”targets,and according to the description of the PCA dimension reduction steps,redundant targets can be eliminated.The optimization results after dimension reduction are given in Fig.1,and the Pareto front is more consistent with the analytical solution.The comparison of optimization convergence process in Fig.3 can also show the insufficient performance in dealing with multi-objective designs.

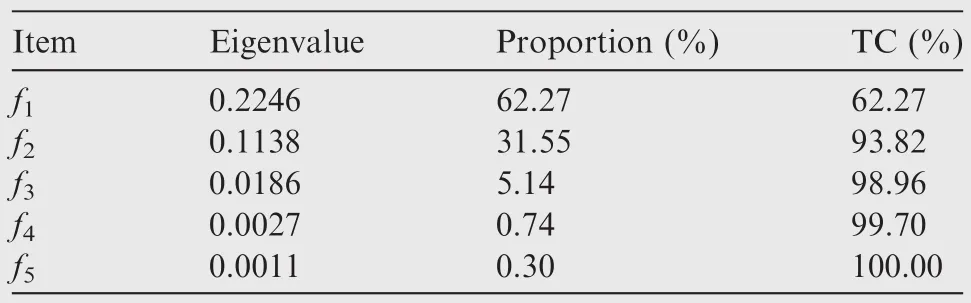
Table 2 Eigenvalue and proportion of each component contribution.

2.3.2.Object dimensional reduction for aerodynamic optimization

In addition,optimization on a supercritical airfoil is tested to further exhibit the ability of PCA in multi-objective aerodynamic optimization and provide a more adequate illustration for the application to complex configuration.High lift-todrag ratio,favorable drag divergence,buffeting and pitch moment characteristics are the basic requirements for a supercritical airfoil with high performance.So,supercritical airfoildesign is a typicalmulti-objective optimization design problem.

Table 1 Eigenvector.

The typical design status of a supercritical airfoil is Mach numberMa=0.7115,liftcoefficientCL=0.63,heightH=10 km,Reynolds numberRe=2.0×107.

According to the design requirements,a mathematical model of multi-objective optimization is specified to test the rationality and validity of the PCA method:

Latin hypercube experimental design and Delta_CST parameterization method were used for sampling.13,14Fig.4 is the near-wall grid distribution for CFD analysis.In this paper,a Navier-Stokes solver for multi-block structured grid is served as the three-dimensional flow field analysis module,in which second-order Roe MUSCL scheme15,k-ω-SST turbu-lence model16,LU-SGS implicit time marching,and multi-grid accelerating convergence technique were adopted.

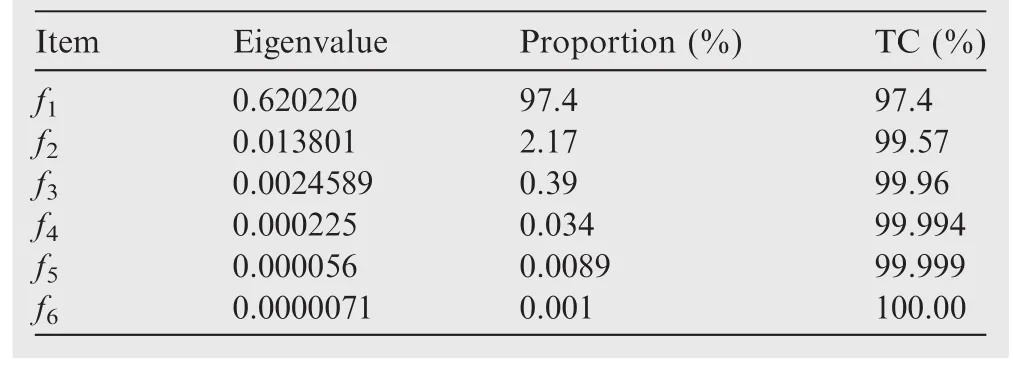
Table 3 Eigenvalue and proportion of each component contribution for airfoil case.

Principal component analysis is performed on the sample set,and the principal component and redundant component will be identified according to the set threshold value TC=0.9.

Fig.5 shows the principal component analysis results and they-axis parameterrepresents the contribution proportion of each eigenvalue,and Tables 3and 4 give the corresponding characteristic vectors.It can be seen that the proportion of the first principal component contribution has met the threshold requirement,reaching 97.4%.

Then the redundant targets can be identified according to the first principal component.By using PCA-based dimension reduction steps described above,it can be determined that the pitch moment objective functionf4and the drag objective functionf5are not redundant targets,which means that the correlation between the two targets is weak.In supercritical airfoil design,in fact,requirements of drag reduction and pitch-moment control are contradictory.After-load of the airfoil,for one thing,drops the suction peak on upper surface so as to control the intensity of shock wave,and as consequence,supplies the lift and reduces the drag.But for another,it brings a larger pitch moment at the same time.From this angle of view,the analysis results from PCA are consistent with the physical mechanism.

Fig.6 shows the projected Pareto front in typical coordinate,and for the redundant objects,the correlation can be analyzed between any two specialized objective functions,such as the objective functionf1andf2.From the eigenvectors,those two objects have the same sign and thus obviously strong relevance,which can also be concluded from Fig.7(a),which shows the comparison between projected Pareto fronts(though the quality is poor)and the linear fitting in thef1-f2coordinate.Similarly,the objective functionsf3andf5also display an obvious correlation(Fig.7(b)).In those two object groups(f1vsf2andf3vsf5),the Mach numbers are relatively closed,which leads to similar flow mechanism,and the principal component analysis results recognize this feature satisfactorily.On the contrary,objective functionsf2andf5can be regarded as an opposite example to further verify the validity of principal component analysis in reflecting physical mechanism.The flow characteristics and Mach numbers of the two objective functions are totally different,namely the main drag component inf2is profile drag,while inf5it is wave drag and profile drag(but not dominant).Therefore,the correlation between the two objects is weaker due to the existence of the wave drag,which can be seen from the eigenvectors and Fig.7(c).

Table 4 Eigenvector for airfoil case.

3.Verification of 3D Navier-Stokes solver

In this chapter,DPW-4 CRM wing-body-tail configuration was taken as CFD validation case.17,18Because the Mach number in wind tunnel test of this model was identical with the wide-body aircraft in subsequent chapter,it can be used as test case for CFD platform verification in aerodynamic design.The computational grid consists of 60 blocks and 15 million cells,andy+is close to 0.5.The computational state isMa=0.85,CL=0.5,Re=5.0×106.Figs.8 and 9 give the wall pressure coefficientCpcontours,and pressure distribution comparison between CFD results and experimental data at typical spanwise stations.It can be seen that the computational results agree well with the wind tunnel test.

4.Multi-objective aerodynamic optimization of wide-body aircraft based on PCA

The research work in this paper is carried out based on Aircraft multi-disciplinary DEsign(AMDEsign)platform,which is developed by aerodynamic optimization research group in China Aerodynamics Research and Development Center.The design platform includes aerodynamic multi-objective module and multi-disciplinary module.Adjoint optimization module,high and low fidelity analysis module of aerodynamics,stealth and structure weight are embedded in this platform(see Fig.10).

On the basis of the above research and to prove the engineering practicability of the method in this paper,aerodynamic multi-objective module of AMDEsign platform was applied to optimization design for a 300-seat wide-body aircraft(see Fig.11).The large scale distributed computation is carried out on the high performance cluster,in which 3000 cores are scheduled(Fig.12).Multi-block structured grid with 23 million cells is generated as baseline grid for fine design(see Fig.13).In optimization design,multi-region free form deformation(Multi-FFD)technology19,20and radial basis function and transfinite interpolation(RBF-TFI)grid deformation technique21are utilized.Figs.14 and 15 are the distribution schematic of FFD lattice.

There are 80 design variables in the wing optimization,and the yellow FFD lattices near the horizontal tail will be rotated around a fixed axis to realize pitching moment trimming(Fig.15).So a total of 81 design variables with 0.5%cfor the design space are used,wherecis local chord length of the wing.

The main components of the wide-body aircraft include supercritical wing,fuselage,nacelle,pylon,inner/outer culvert,horizontal and vertical tail.Its cruise lift coefficient is 0.48,and the design goal is to improve lift-to-drag ratio in trimming condition with the drag divergence Mach number greater than 0.87.Then the main objectives of the optimization design can be summarized as follows:

(1)Increasing the cruise lift-to-drag ratio at the design lift coefficient.

(2)Improving the drag divergence characteristics.

(3)Extending the buffeting boundary.

Table 5 Eigenvector for wide-body aircraft case.

(4)Realizing overall moment trimming by horizontal tail

(5)Wing root bending moment would be less than or equal to 1.03bending moment.

For the buffeting lift coefficient in this paper,the judgment standard provided by literature21is adopted,in which the curve slope of pitch moment and the change of wing separation region are considered as the criteria.Because the drag will obviously increase when the buffeting occurs,the buffeting characteristics can be improved by optimizing the drag at buffeting lift coefficient.Therefore,the basic optimization model and constraints can be expressed as the following form:

wheretmax,t0are the maximum thickness of the airfoil and the initial thickness respectively,ω1,ω2are the weight coefficient,

andCL,Cm,Cmbend,CD,and Geom constraint are the cruise lift,pitching moment,root bending moment,drag coefficient,target drag coefficient and geometry constraint respectively.

Table 6 Drag coefficient of different configurations.

Table 7 Root bending moment of different configurations.

Principal component analysis was carried out for the samples obtained by design of experiment(DOE).Table 5 lists the analysis results and Fig.16 gives the contribution proportion of each eigenvalue.It can be seen that the contribution of the first principal component has met the threshold requirement,reaching 91.9%.According to the PCA analysis step,for the present set of threshold,the 3rd,4th and 5th targets are relatively ‘redundant”.From the ‘view” of the first principal component,the 4th and 5th targets are correlated,and the correlation also exists between the second and third objects.It is needed to note that different from the airfoil case in Section 1.3,the pitch moment of this configuration is determined primarily by the installing angle of horizontal tail with little trimming drag(-3–5 counts approximately).So the contradiction between the pitch moment and lift-to-drag ratio is weaker compared with single airfoil.

According to the PCA vector results,f1,f2andf5should be regarded as the primary objects,but the objectf5was extracted from the vector elementV3,so it can be used as a penalty function combined withf1,and then the optimization model of objective-reduction was expressed as

where is the weight coefficient,F1,F2are the new weighted objective function obtained by PCA.After the dimension reduction by PCA,the redundant targets are transformed into constraints.In the design process,the constraint of airfoil section thickness is combined with objectivef1as the penalty function.As the prediction accuracy of surrogate model is a bottleneck technique for high dimensional design space,distributed CFD analysis module was used in optimization process in this paper.The standard MOPSO and PCA-MOPSO algorithms are used to iterate 60 generations respectively for comparison.

Pareto front convergence of different methods with the same iteration is given in Figs.17 and 18.Before the dimension reduction,the Pareto front fails to converge with very slow advancing speed,while the PCA-MOPSO method gives obvious front,which means that the method is much more efficient under the same design requirements.Two configurations A,B with better comprehensive performance were singled out,whose pressure distributions at typical spanwise stations and drag divergence characteristic are shown in Fig.19.The different sections pressure distributions of configurations A and B was are shown in Fig.20.The drag coefficients and root bend moment of configuration A and initial configurations are given in Tables 6 and 7.It can be seen that the lift-to-drag ratio and drag divergence are improved obviously with tiny root bending moment increasing.For configuration A,the pressure distributions after optimization are weak shock waves,and tend to be similar along spanwise direction.

Fig.21 gives the comparison of pressure distribution at typical spanwise stationsy/bbetween the initial configuration and configuration A.It is known that with the increase of the Mach number,the shock wave will be enhanced and move backwards with cruise angle of attack decreasing,while the ‘bump”shaped pressure distribution of trailing edge of the wing can restrain this phenomenon and improve the drag divergence.In fact,this kind of design can also be reflected in the engineering inverse design.In addition,the ‘bump” shaped pressure distribution and the ancillary forward pressure recovery are also beneficial to extend the buffeting boundary,which gives another evidence for correlation betweenf3andf2from PCA analysis.Figs.22–24 show the surface streamline and curve of pitching moment of initial and configuration A.According to the criterion,the buffeting occurs atCL=0.60 and atCL=0.64 for initial and configuration A respectively.From the separation region as well as drag divergence characteristic,it can be seen that the buffeting boundary of the optimized configuration is improved.It needs to be noticed that in this optimization example,PCA analysis shows relatively low importance of buffeting object(ranked 3rd)and correlation with objectf2.The reason is that,relative to the airfoil,buffeting characteristic is more sensitive to the distribution of the twist angle,while the twist angle distribution is obtained in advance through the optimization of load distribution and does not change during the above aerodynamic optimization process.This just once again illustrates the validity and rationality of the PCA method.In summary,based on PCA dimension reduction,notonly thelift-to-drag ratio is improved,but also the ‘redundant” design requirements are satisfied.

5.Conclusions

In this paper,the PCA method application in multi-objective aerodynamic optimization has been researched.The results affirmatively show that dimension reduction for multiobjective design is valid and rational compared to traditional method.

(1)The DTLZ5 function testing results show that PCA method can identify the redundant objects and reduce the object dimension effectively.

(2)Multi-objective principal component analysis for supercritical airfoil further illustrates that the redundancy identification and correlation analysis are consistent with physical mechanism of the flow.

(3)The effectiveness of dimensionality reduction of PCA is further confirmed by the design results on multiobjective optimization of wide-body aircraft.Compared with original configuration,the optimal lift-to-drag ratio improves around 6%,and the drag divergence Mach number is larger than 0.87 with satisfaction of buffeting boundary requirement.

In summary,the dimension reduction for aerodynamic multi-objective optimization based on PCA is conducive for designer to make a reasonable decision for multi-objective problems by effectively reducing object dimension and complexity and improving the visual level of non-dominated solutions without losing any dominating feature of the optimization problem.It can be predicted that PCA will play an important role in the higher dimensional and more complex multi-objective optimization problems,such as flight vehicle aerodynamics,structure,stealth,control and other disciplines,multidisciplinary and multi-objective comprehensive optimization.

Acknowledgements

This study was financially supported by the National Natural Science Foundation of China(No.11402288)and technically supported by High Performance Computing Center in China Aerodynamics Research and Development Center.Hereby,the authors would like to express their heartfelt thanks to these organizations and individuals!References

1.Knowles J,Corne D.Quantifying the effects of objective space dimension in evolutionary multiobjective optimization.In:Obayashi S,Deb K,Poloni C,Hiroyasu T,Murata T,editors.Proceedings of the international conference on evolutionary multicriterion optimization(EMO-2007);2007 Mar 5–8;Matsushima,Japan.Berlin:Springer;2007.p.757–71.

2.Schutze O,Lara A,Coello C.On the influence of the number of objectives on the hardness of a multiobjective optimization problem.IEEE Transact Evolut Comput2011;15(4):444–55.

3.Purshouse RC,Fleming PJ.Evolutionary multi-objective optimisation:an exploratory analysis.In:Proceedings of the 2003 IEEE Congress on evolutionary computation;2003 Dec 8–12;Canberra,Australia.Piscataway(NJ):IEEE;2003.p.2066–73.

4.Abdi H,Williams LJ.Principal component analysis.Wiley Interdiscipl Rev:Comput Stat2010;2(4):433–59.

5.Jolliffe I.Principal component analysis.New York:John Wileyamp;Sons;2005.

6.Dongg JC,Yang TJ,Li XH,Dai L.Applications of principal component analysis in excitation source identification.J Vibr Shock2013;32(24):157–63.

7.Cho MS,Kim KJ.Indirect input identification in multi-source environments by principal component analysis.Mech Syst Signal Process2002;16(5):873–83.

8.Servie`re C,Fabry P.Blind source separation of noisy harmonic signals for rotating machine diagnosis.J Sound Vibr2004;272(1–2):317–39.

9.Deb K,Saxena DK.On finding Pareto-optimal solutions through dimensionality reduction for certain large-dimensional multi-objective optimization problems.Kanpur:Kanpur Genetic Algorithms Laboratory;2005.Report No.:2005011.

10.Deb K,Saxena DK.Searching for Pareto-optimal solutions through dimensionality reduction for certain large-dimensional multi-objective optimization problems.In:Proceedings of the 2006 IEEE congress on evolutionary computation;2006 Jul 16–21;Vancouver,Canada.Piscataway(NJ):IEEE;2006.p.3353–60.

11.Kennedy J,Eberhart RC.Particle swarm optimization.In:Proceedings of IEEE international conference on neural networks.Piscataway(NJ):IEEE;1995.p.1942–8.

12.Khare V,Yao X,Deb K.Performance scaling of multi-objective evolutionary algorithms.In:Foseca CM,Fleming PJ,Zitzler E,ThieleL,DebK,editors.Proceedings of the international conferenceon evolutionary multi-criterion optimization(EMO-2003);2003 Apr 8–11;Portugal,Faro.Berlin:Springer;2003.p.376–90.

13.Kulfan BM.A universal parametric geometry representation method –‘CST”.Reston(VA):AIAA;2007.Report No.:AIAA-2007-0062.

14.Ceze M,Hayashi M,Volpe E.A study of the CST parameterization characteristics.Reston(VA):AIAA;2009.Report No.:AIAA-2009-3767.

15.Toro EF,Spruce M,Speares W.Restoration of the contact surface in the HLL-Riemann solver.Shock Waves1994;4(1):25–34.

16.Menter FR.Two-equation eddy-viscosity turbulence models for engineering applications.AIAA J1994;32(8):1598–605.

17.Wang YT,Zhang SJ,Meng DH.Numerical simulation and study for DPW4 wing/body/tail.Acta Aerodyn Sinica2013;31(6):739–44[Chinese].

18.Vassberg JC,Dehaan MA,Rivers SM,Wahls RA.Development of a common research model for applied CFD validation studies.Reston(VA):AIAA;2008.Report No.:AIAA 2008–6919.

19.Huang JT,Gao ZH,Zhou Z.An improved adaptive sampling and experiment design method for aerodynamic optimization.Chin J Aeronaut2015;28(5):1391–9.

20.Samareh JA.Aerodynamic shape optimization based on free-form deformation.Reston(VA):AIAA;2004.Report No.:AIAA-2004-4630.

21.Spekreijse SP,Prananta BB,Kok JC.A simple,robust and fast algorithm to compute deformations of multi-block structured grids.Amsterdam:National Aerospace Laboratory NLR;2002.Report No.:NLR-TP-2002-105.

15 June 2016;revised 6 September 2016;accepted 27 September 2016

Available online 7 June 2017

*Corresponding author.

E-mail address:hjtcyf@163.com(J.HUANG).

Peer review under responsibility of Editorial Committee of CJA.

Production and hosting by Elsevier

http://dx.doi.org/10.1016/j.cja.2017.05.003

1000-9361©2017 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.

This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

Aerodynamic optimization;

Dimensional reduction;

Improved multi-objective

particle swarm optimization(MOPSO)algorithm;

Multi-objective;

Principal component analysis