构建物理图景,探究动力学临界问题
王孟辰


摘 要:在物理学中,临界问题广泛存在于动力学和电磁学等领域。解决临界问题时,要分析清楚物理变化的过程, 形成清晰的物理图景, 找出临界状态, 分析临界条件, 求出临界极值。本文主要利用物理图景进行动力学临界问题的探究。
关键词:动力学;临界问题;物理图景
所谓临界问题,一般是指物体的运动从一种形式转变为另一种形式,或者一种物理现象转变为另一种物理现象,或者一种物理过程转变为另一种物理过程的过程中,存在着分界限的问题[1]。在临界状态下,某种物理现象“恰好可以出现”或者“恰好不能出现”,在这个过程中出现的最大值或最小值被称为临界值。临界问题通常难度系数大,综合性强,往往涉及到动力学和电磁学的知识。下面具体对动力学临界问题的处理进行物理学研究。
一、分析临界问题的方法
在动力学中,临界问题是常见的问题,经常出现在匀变速运动、共点力平衡、牛顿运动定律中的题目中。 解决动力学临界问题的重点就是要建立物理模型,形成清晰的物理图景。物理图景是在感知的基础上通过形象思维与物理世界相互作用而形成的心智图画[2], 有助于充分还原题目的物理情境和物理模型,准确把握各个力变化的动态过程,挖掘隐含条件 ,找出转折点,明确承前启后的物理量,进而找到达到极值的条件或者是临界条件,从而突破临界问题的难点,最终得出临界极值。下面结合摩擦力临界值问题和竖直平面内圆周运动的临界问题的解决来阐述物理图景在解决动力学临界问题的作用。
二、摩擦力临界值问题
在解决与摩擦力有关的临界问题时,通过对物理过程的分析, 形成清晰的物理图景,找到物体间相对滑动的临界条件,也就是静摩擦力达到最大值,从而找到解决问题的突破口。
1. 提出问题
(2014. 新课标全国卷I, 20)如图,两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴OO′的距离为l,b与转轴的距离为2l。木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g。若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )
2. 分析问题, 明晰物理过程, 构建物理图景
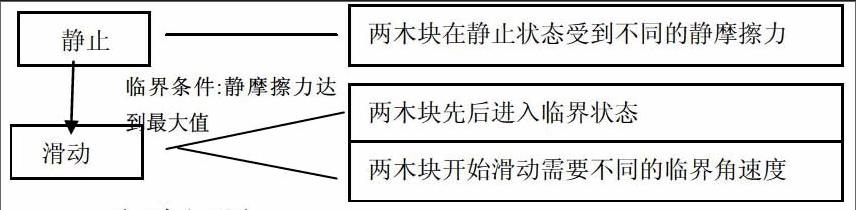
木块a和木块b放在水平转盘上,始终随盘一起做匀速圆周运动, 小物块受到重力、支持力和摩擦力三个力。向心力是物体做圆周运动所需要的力,由静摩擦力提供,所以摩擦力的方向始终沿半径指向圆心,与速度方向垂直; 根据f静=mRω2,可知,木块a和木块b放的位置不一样,运动半径R 就不一样,需要的向心力也不一样,在开始滑动之前,受到静摩擦力大小也不同,因此它们产生滑动的临界角速度也不一样。通过分析,认识到应弄清楚两个木块在进入临界状态之前受到的静摩擦力,及静摩擦力达到最大值时,两木块开始滑动所需要的不同临界角速度。
3. 解决问题
两木块在进入临界状态之前受到的静摩擦力的比较: 木块a和木块b都随着水平转盘一起做匀速圆周运动。两物块都相对圆盘静止时,共轴转动,角速度相等,木块a的运动半径小于木块b,所以发生相对滑动前木块a受到的静摩擦力小于木块b受到的静摩擦力,因此选项B错误。
两木块在进入临界状态先后的比较:当最大静摩擦力提供的向心力为f静=mRω2,木块进入开始滑动的临界状态.由于木块b的运动半径是木块a的2倍,所以木块b最先达到最大静摩擦力,最先滑动,因此选项A正确。
两木块开始滑动所需的临界角速度:
竖直面內物体做圆周运动的临界问题的研究
竖直平面内圆周运动的临界问题主要包括绳控模型,杆控模型和拱桥模型。研究竖直平面内圆周运动的临界问题,首先要确定该问题属于哪一种模型,然后确定临界点,再研究运动状态,最后进行受力分析和过程分析。
1. 提出问题
如图所示, 光滑管形圆轨道半径为R(管径远小于R),小球a、b大小相同,质量均为m,其直径略小于管径,能在管中无摩擦运动.两球先后以相同速度v通过轨道最低点,且当小球a在最低点时,小球b在最高点,以下说法正确的是( )
2. 分析问题, 明晰物理过程, 构建物理图景
小球a 和小球 b 在管内转动,则内管可对小球提供向上的支持力,故可看作是杆模型;只要小球b的速度大于零, 就能通过最高点;而当向心力等于重力时,小球b对轨道没有压力,由向心力公式可求出小球b在最高点的速度;再由机械能守恒定律求得小球a在最低点的速度及所需要的向心力,进而求出小球a与小球b压力的差值。
3. 解决问题
定模型, 明确临界条件。小球在管内转动,则内管可对其提供向上的支持力,故可看作是杆控模型;因此, 小球在最高点的速度只要大于零,即可通过最高点,故选项C错误。
研究小球的运动状态, 求出小球b在最高点时和小球a在最低点的速度, 并进行受力分析。
应用机械能守恒定律求出最低点与最高点压力的差值。
结语
综上所述,可以看出解决动力学物理临界问题的关键就在于清晰有序地分析物理过程,恰当地将复杂的对象或隐含的过程向理想化模型转化,形成清晰的物理图景,确定临界条件,进而将物理知识和数学知识结合有效地实现对问题的解决。
参考文献
[1]. 杨桦,潘天俊,孟卫东 临界问题面面观--谈物理学科临界问题的分析方法[J].高中数理化, 2010(1).
[2]. 项华;李永艳 物理图景素养的培养:模型、问题与对策[J]. 课程.教材.教法;2008(3)endprint

