从另一角度思考二项式定理

江西省上饶中学 吕 峰

从另一角度思考二项式定理

江西省上饶中学 吕 峰

二项式定理是高中重要的一节内容。尽管每个教师都有自己的教学特点，但在处理二项式定理这一节时，方式都比较统一。本文旨在提供另外一个讲解二项式定理的思路，以供各位同仁参考。

二项式定理；卡亚姆

二项式定理是高中课本中重要的一节内容。这节的内容是安排在排列组合之后学习的，这是因为它的学习要基于排列组合。对于这节课的教学，课本上是这样展开的：先从几个特殊的n值入手，再推出一般结论。

比如当n=2时，（a+b）2=a2+2ab+b2，在没有合并同类项前，它有四项，分别是a2、ab、ba、b2，每一项的系数都是1，而合并了同类项后，有三项，分别是a2、ab、b2，系数分别是1、2、1，跟之前的有区别，产生区别的原因是因为合并了同类项。现在从排列组合的角度看这些系数的产生。要确定某一项，必须从第一个括号中选一个字母，比如确定ab这一项的系数，要么从第一个括号中选一个a，这样的话就必须从第二个括号中选一个b，或者先从第二个括号中选一个a，那么第一个括号中必须选b，这样总共有2种选法，也就是

种选法，这也是ab这一项的系数。用这种方法，我们推广到一般结论去，从而得出二项式定理。

用这种方法处理二项式定理，好处很明显，学生很容易懂。虽然如此，但笔者在用这种方法上过这节内容的课后，总感觉不痛快，单单那个像绕口令一样的话语“要……，要么……，就……”就让人说出来气喘吁吁，也违背了数学教学应简洁明了的原则。于是，笔者就想能不能用一种更自然的方法教学二项式定理。翻阅了大量资料，比较了一些方法，觉得卡亚姆的方法很自然，而且跟排列组合联系得很紧密，从而也让知识的过渡更自然。

卡亚姆的二项展开式：

当n 是任意正整数时，求以a 和b 的幂表示的二项式（a + b ）的n 次幂。

解：为了确定二项展开式，写出：

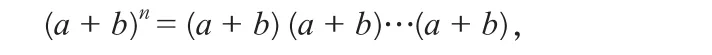
这里，右边包含n 个相同的（a + b）的乘积，像人们所了解的那样，括号的乘式包含从每一括号中选出一项，得出所选项的乘积，并继续该过程，直至取尽所有可能的选择，最后将得到的乘积加在一起。

这类乘积的形式如下：

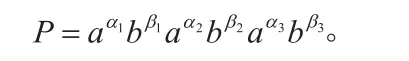
其中，从开头的α1个括号中各取出因子a，从随后的β1个括号中各取出因子b，再从其后的α2个括号中各取出因子a……在这种情况下，α1+β1+α2+β2+……等于现有的括号数，即n。

除上述的这种方法外，一般还有许多其他方法可以求得乘积P。例如，从前面α个括号中取出a，而从后面β个括号中取出b；从前面β个括号中取出b，而从后面α个括号中取出a，等等。如果乘积P 在上述方法中出现C 次，C 被理解为代表一个最初的未知数，那么

表示二项展开式的一项。其他各项除了指数α与β以及系数C 不同外，都具有相同的形式。因此，α+β总是等于n。

该题的关键是确定所谓的“二项系数”C，即回答问题：在二项展开式中，乘积 出现多少次？

为了解答这个问题，首先按照从括号中最初选定的顺序逐个地写出乘积中的因子a 和b：

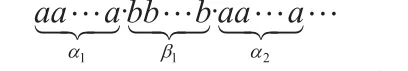
这就是出现α个相同元素a 与β个相同元素b 的n 个元素的排列。这些元素排列种数的多少与从n 个（a + b）的连乘式中得到的项P一样。

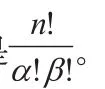
从上面的解答过程中可以看出，卡亚姆所采用的方法完全是基于排列组合的，从之前学习的排列组合中可以找到很多模型与之对应。比如：有3本相同的数学书，4本相同的语文书，共有几种叠放方式？学生对类似的模型都很熟悉，当然可以轻易理解卡亚姆的二项展开式。教师在这里教学时，实际上只需要让学生联想之前学习过的一些排列组合模型，相信学生就可以很快得出结论。用这种方法教学，既让教师教得轻松，而且可以让学生学得轻松。何乐而不为呢！