并联驱动机械腿运动学静力学性能评价及几何参数设计
张金柱,金振林,张天浩
并联驱动机械腿运动学静力学性能评价及几何参数设计
张金柱,金振林※,张天浩
(燕山大学机械工程学院,秦皇岛066004)
为了拓展农业机器人的作业场合,该文对一种三自由度六足腿式机器人并联驱动机械腿机构进行了运动学静力学性能评价及几何参数优选。首先,求解了足端线速度和角速度之间的耦合关联矩阵,定义了该腿部机构的运动学性能评价指标,绘制了该指标的分布图。其次,建立了腿部机构驱动静力学模型,分别利用机械腿在重力方向的最大承载力和驱动关节的最大扭矩定义了该腿部机构在软、硬地面下的驱动静力学性能评价指标。基于线性空间理论求解了驱动机构的约束雅克比矩阵,定义了约束静力学性能评价指标,通过绘制驱动与约束静力学性能评价指标分布图揭示了该腿部机构静力学性能在工作空间内的变化规律。再次,结合各项运动学和静力学性能评价指标,利用搜索法对该腿部机构几何参数进行了多目标优选,并给出了一组较好的几何参数。优选结果表明:平行四边形铰链长连杆及连接连杆的几何参数分别为330 mm和140 mm,地面接触连杆几何参数为320 mm时,腿部机构的综合性能得到改善,具体表现为运动性能提升了5.46%,重力方向最大承载力提升了18.02%,驱动关节的最大扭矩减小了6.33%。该研究结果可为该六足机器人步态规划及控制和应用提供参考。
机器人;运动学;静力学分析;并联驱动腿;性能评价;参数设计
0 引 言
农业机械化是农业生产从粗放型向集约型转变的重要条件之一,也是实现农业现代化的重要标志[1-2]。农业机器人在田间、鱼塘、养殖厂等农业环境中自动作业离不开农业运载平台的支撑[3]。现有的应用较为成熟的农业运载平台的主要类型为轮式、履带式和导轨式[4-5]。然而它们在作业过程中均需与连续的地面接触,在非结构地面或生长有农作物的离散地面上难以充分发挥其应有的效能。腿式机器人作为一种新型农业运载平台[6],拥有占地面积小、落足点离散、对地面适应性好等特点,可作为现有运载平台的一种补充,以拓展机器人在农业领域的作业场合。
机械腿是腿式机器人运动和承载的关键部件[7]。机械腿性能的好坏直接决定着腿式机器人的作业能力[8-9]。对于在非结构农业环境作业的重载机器人而言,运动学静力学性能作为机械腿的主要性能,在评价腿部机构“先天”性能的可行性和“后天”的尺度参数优化方面具有重要的作用。目前,关于并联机构运动学和静力学性能方面研究较多,如杨龙等[10]利用拆杆法分析了二自由度球面机构的静力学性能;汪满新等[11]通过构建解耦格式的全雅可比矩阵,分析了3-SPR并联机构的运动学性能,给出了特定几何及运动性能约束下的几何参数可行域;李剑锋等[12]分析了2-UPS/RR并联机构的运动学性能,并以机构的可操作度、灵活性及刚度特性为目标对机构的驱动方式进行了优选;曲海波等[13]利用螺旋理论分析了4-RRS冗余球面并联机构的静力学,并以支链关节力和力矩的最大值为评价指标对比分析了该机构在冗余与非冗余状态的静力承载性能;崔国华等[14]利用封闭矢量法和D-H法构建了3-PUS+UP并联机构的全雅可比矩阵,并建立了该机构的运动灵巧性最优工作区域;荣誉等[15]分别利用封闭矢量法和螺旋理论构建了(U+UPR)P+UPS并联机构的驱动及约束雅可比矩阵,并以驱动和约束静力性能为目标对该机构进行了多目标优化设计。上述研究表明了运动学及静力学性能研究有助于并联机构在工程上的合理及广泛应用,具有显著的工程研究价值[16]。
此外,在多足机器人腿部机构运动学静力学性能方面,荣誉[15]、Pan[17]、金波[18]和崔冰艳等[19]做过深入的研究,然而上述研究均集中在腿部机构自身的运动与力传递特性方面,没有考虑机器人工作的地面类型对机械腿作业的影响。为了提高机器人对环境的适应性,在分析腿部机构自身性能的同时考虑地面类型对其的影响显得十分必要。本文分别利用虚功原理和线性空间理论建立了整个腿部机构的驱动广义力传递矩阵和并联驱动机构的约束广义力传递矩阵,在考虑腿部机构工作的地面类型的前提下,基于运动雅可比矩阵和驱动及约束力传递矩阵定义了腿部机构的运动学和静力学性能评价指标,结合定义的各项性能指标,对腿部机构几何参数进行优选,以期为该腿部机构的样机研制和步态规划及控制提供理论基础。
1 腿部机构及坐标系建立
本文所研究三自由度腿部机构,如图1所示,该腿部机构由驱动机构、行走机构和一个连接球副组成,驱动机构为2RUS+RU并联机构,且3个R为整个腿部机构的驱动副,行走机构为由两个轴线垂直相交的转动副和一个平面平行四边形铰链组成的组合机构(即放大机构)。在2RUS+RU中,2条RUS支链相对于RU支链所在的平面对称布置,在初始状态下,RU支链和放大机构布置于同一竖直平面内。∥表示平行,⊥表示垂直。则机构中杆件和运动副的几何关系有4∥5∥7,6∥35,g⊥6。
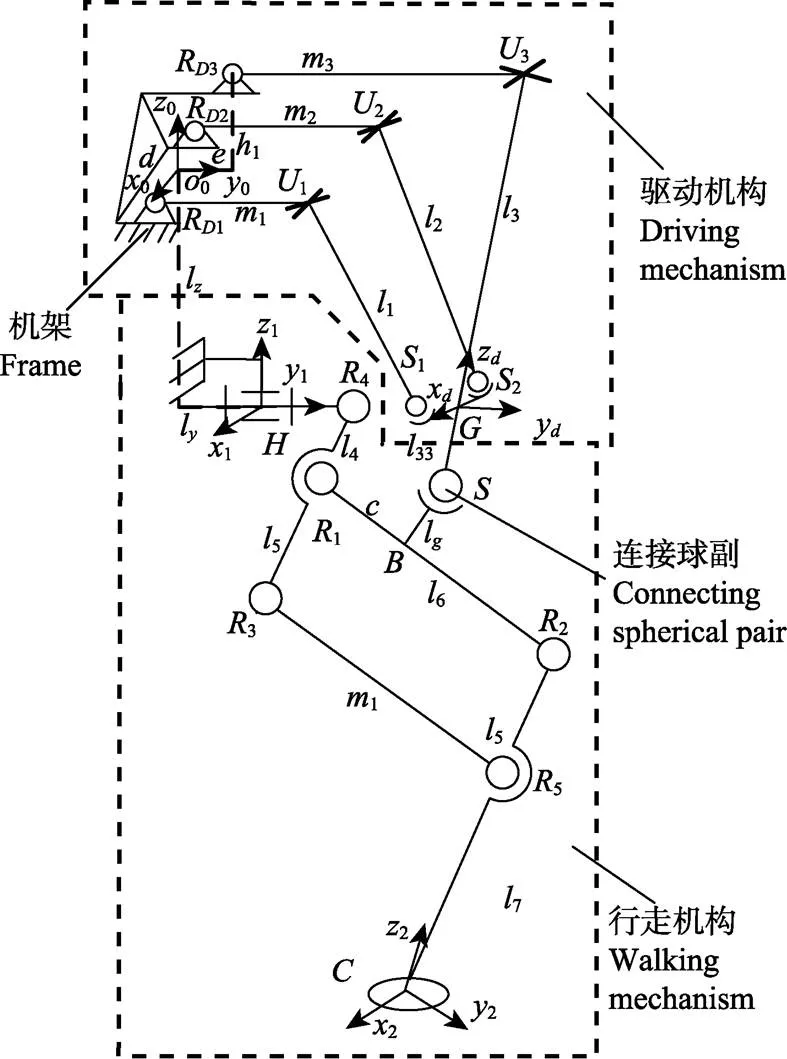
注:RDi (i=1,2,3)为转动副中心点,Ui (i=1,2,3)为虎克铰中心点,Si ( i=1,2)为球副中心点;G为RU支链与动平台的固接点;Ri (i=1,2,3,4,5)为行走机构的各杆件之间的转动副中心点;H 为行走机构与机架连接的转动副中心点;C 为足端点;O0是RD1RD2的中点;H与O0之间的水平和竖直距离分别为ly和lz;设机构的主要几何参数为RDiUi=mi(i=1,2,3),UiSi=li(i=1,2),U3G=l3,R4R1=l4,SiG=a(i=1,2),R1R3=l5,R1R2=l6,R1B=c,SB=lg,R5C=l7,GS=l33,RD1RD2=d,(O0RD3)y=e,(O0RD3)z=h1。
坐标系建立方面,如图1所示,以0为原点建立固定坐标系{}:0-000,其中0∥R1R2,0水平向右;以为坐标原点建立动坐标系{}:-xyz,x∥12,y⊥12,z∥3;以为原点建立参考坐标系{}:-111有1∥0,1∥0;以为原点建立足端连体坐标系{}:-222,有2∥2,2⊥12,2⊥13;0、1和2均由右手螺旋定则确定。
2 腿部机构运动性能分析
2.1 腿部机构雅可比矩阵
由文献[20]可知,腿部机构驱动副R和足端点之间的速度映射关系为

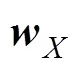
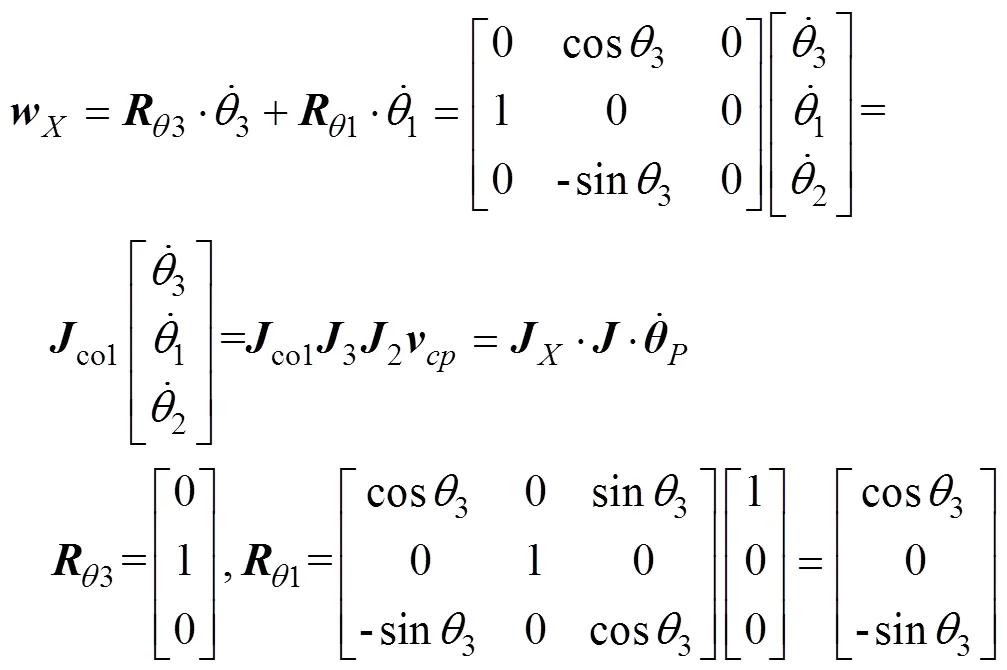
2.2 腿部机构运动性能分析

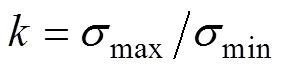
基于机器人总体设计要求和驱动工作空间优化结果[21],首先设定一组机构的几何参数如下(mm):=276,1=70,=0,=55,1=2=220,3=250,33=120,1=2=200,3=200,=110,4=5=200,6=300,7=450,l=190,l=55,g=46.5。基于该几何参数、在限定驱动副转动范围为[-21°,21°],U副与S副的转角范围均为[-45°,45°]的情况下,得足端点在腿部机构工作空间(足端点在工作过程中扫过的点的集合)的不同高度(点在{}中的坐标值)下的分布情况,如图2所示。
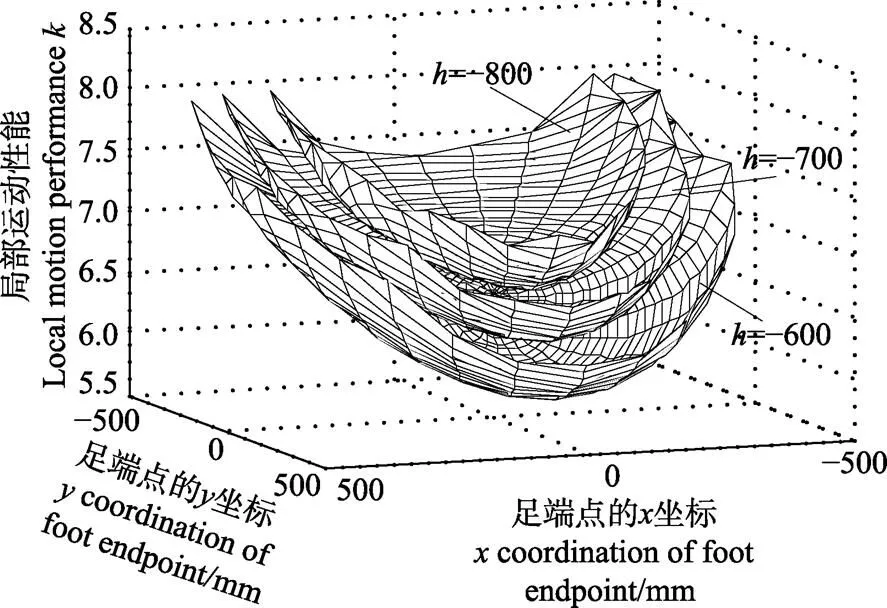
注:h是C点在坐标系{C}中的z坐标值。下同。
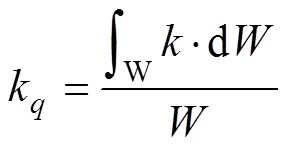
3 驱动静力学分析
3.1 驱动静力学模型
六足机器人具有落地点离散、对地面的适应性强等特点,有应用于多变环境的潜能[22-24]。对于不同环境的地面类型,从足端受力角度可将其分为硬地面和软地面两种,其中硬地面如图3a所示,半球形足端在处于支撑相期间始终与地面保持点接触,只受地面的反作用力;软地面如图3b所示,半球形足端在处于支撑相期间始终镶嵌在地面中,除受到地面对它的作用力外,还有作用力矩。
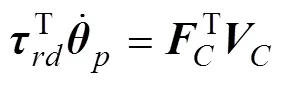
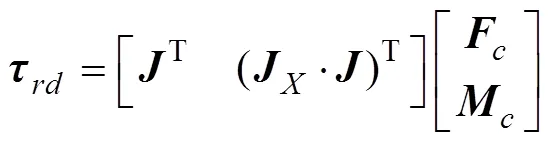
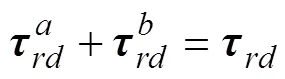
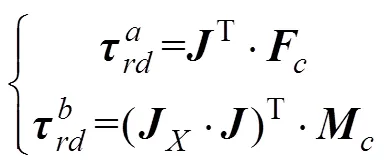

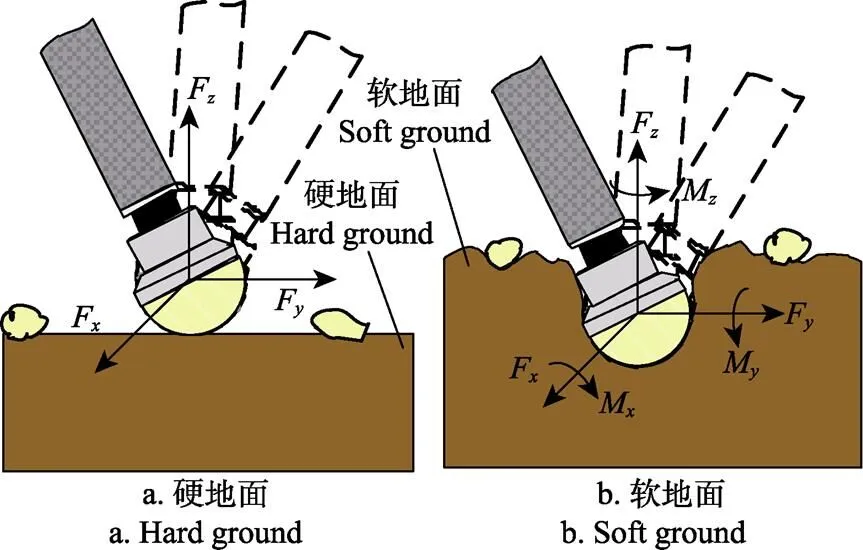
注:Fi(i=x, y, z)是足端作用力在i方向的分量,N;Mi(i=x, y, z) 是地面对足端作用力矩在i方向的分量,N·m。
3.2 约束静力学模型
少自由度并联机构的支链不仅向机构末端传递驱动力,同时还提供约束力。为了衡量驱动机构约束力承载性能,本文采用线性空间理论求解该机械腿的并联驱动机构的约束雅可比矩阵。
由图1可知,机械腿的并联驱动机构由两个无约束RUS分支和一个恰约束RU分支组成。图4为RU分支的单位约束力螺旋。在图4中,坐标系{}:G-xyz为原点为的参考坐标系,且{}在任意瞬间均与{}平行。
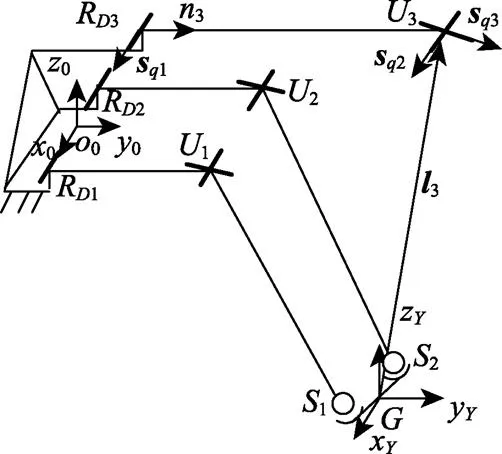
注:sqi(i=1,2,3)分别为RU分支中转动副R和U的三个转动轴线在坐标系{Y}中的方向矢量,n3为杆件RD3U3在坐标系{Y}中的方向矢量,l3为U3在坐标系{Y}中的位置矢量。
根据文献[25]提出的少自由度约束雅可比分析方法,得驱动机构中RU分支的受限变分子空间和约束力子空间的基分别为
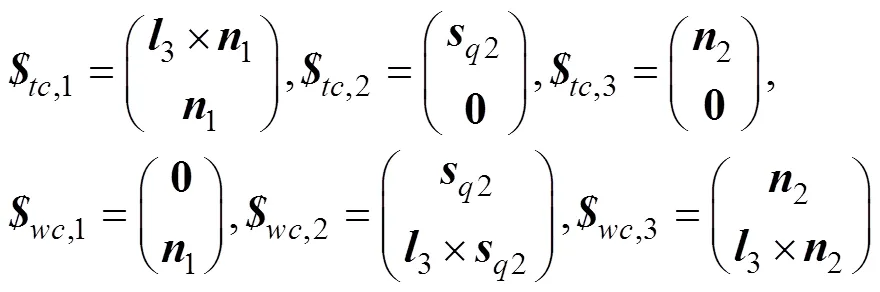
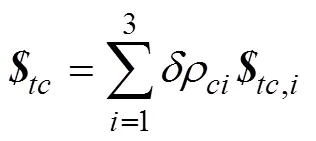
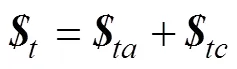
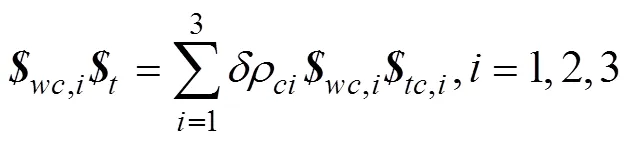
将上式写为矩阵形式为
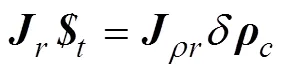
由式(12)得驱动机构的约束雅可比矩阵为
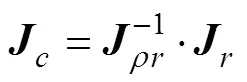
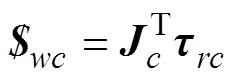
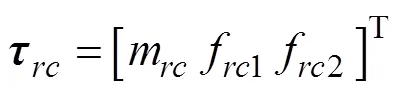
3.3 驱动静力学性能评价
对于多足步行机器人而言,承载能力是其一项重要设计指标,对续航能力,工作效率等方面有重要的影响[26]。经过对多足机器人整体运动规律的研究发现多足机器人的承载能力不仅与腿部机构的力学传递特性有关[27-28],还与足端点的受力状态息息相关。
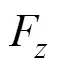


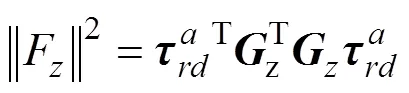
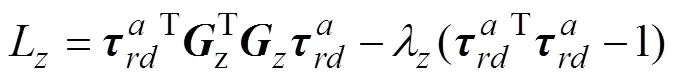
由上式得,足端输出力重力方向分力的极值条件为
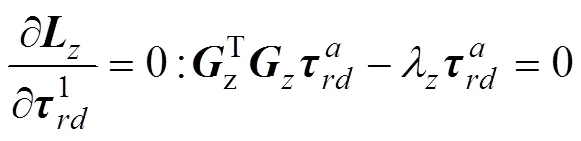
由此得该腿部机构的足端输出力重力方向分力的极值为
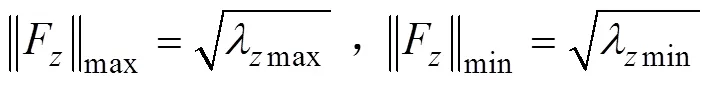
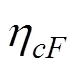

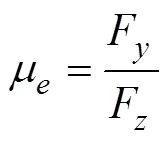
其中额定摩擦系数μ,可以用作判断在某种地面上机器人承载能力能否发挥的检验指标(如果>μ机器人能够充分地发挥其承载能力,否者机器人不能充分发挥其承载能力),也可以作为某种地面上机器人行走步距大小的选择指标。
2)当地面类型为图3b所示的软地面时,此时足端与地面不易打滑,克服足端力矩成为影响腿部承载能力的主要因素之一。此时机器人腿部机构能够工作需满足的额外条件为
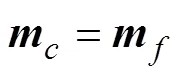
式中为在坐标系{}中的腿部需要克服的外力矩矢量。

也可写为
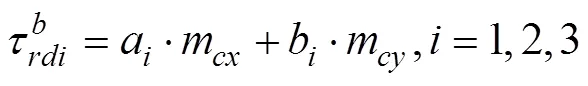
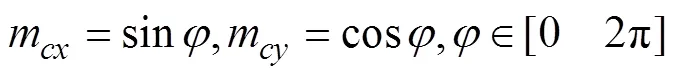
将(26)式带入(25)式,并求其最值可得
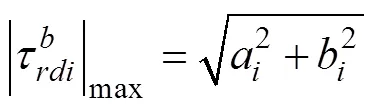

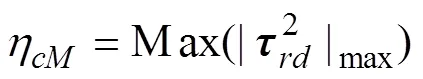
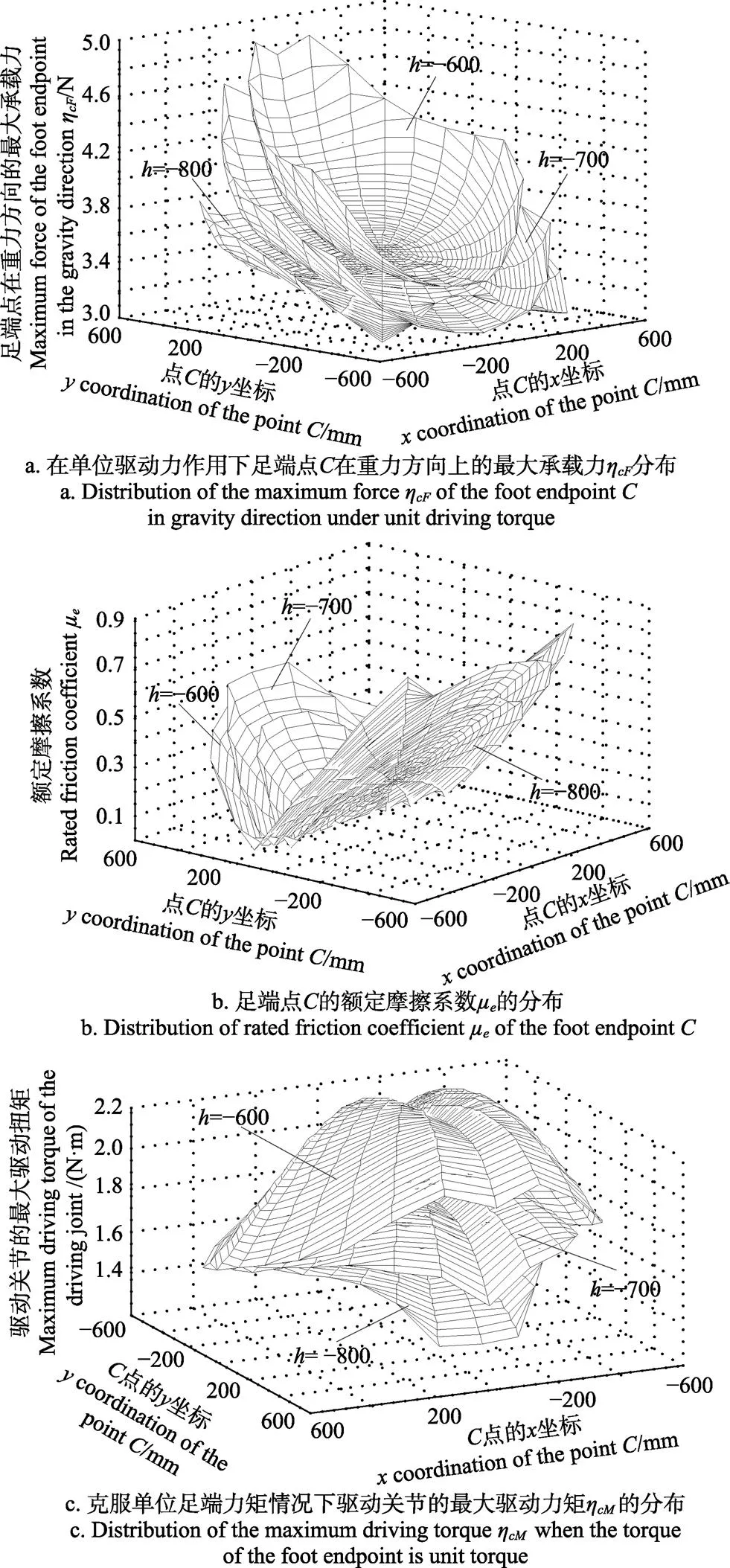
图5 当足端点C的纵坐标为h时足端点在重力方向的最大承载力ηcF,足端的额定摩擦系数μe和驱动关节的最大驱动力矩ηcM的分布
综上所述,承载能力除与腿部机构的力学传递性有关外,还与行走的地面类型有关。他们不仅能够衡量该机器人在特定工作环境下的承载能力,而且能够为该多足机器人设计及在特定承载下的步态规划和控制提供参考。

3.4 约束静力学性能评价
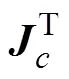
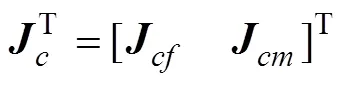
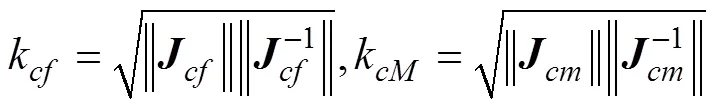
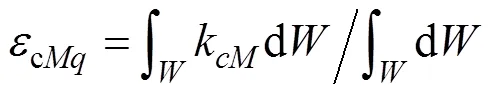
综上腿部机构运动学/静力学性能分析结果,可得腿部机构在000面内的综合性能较好。在机器人腿部布局时,000面更适合作为机械腿的矢状面(主运动平面)。
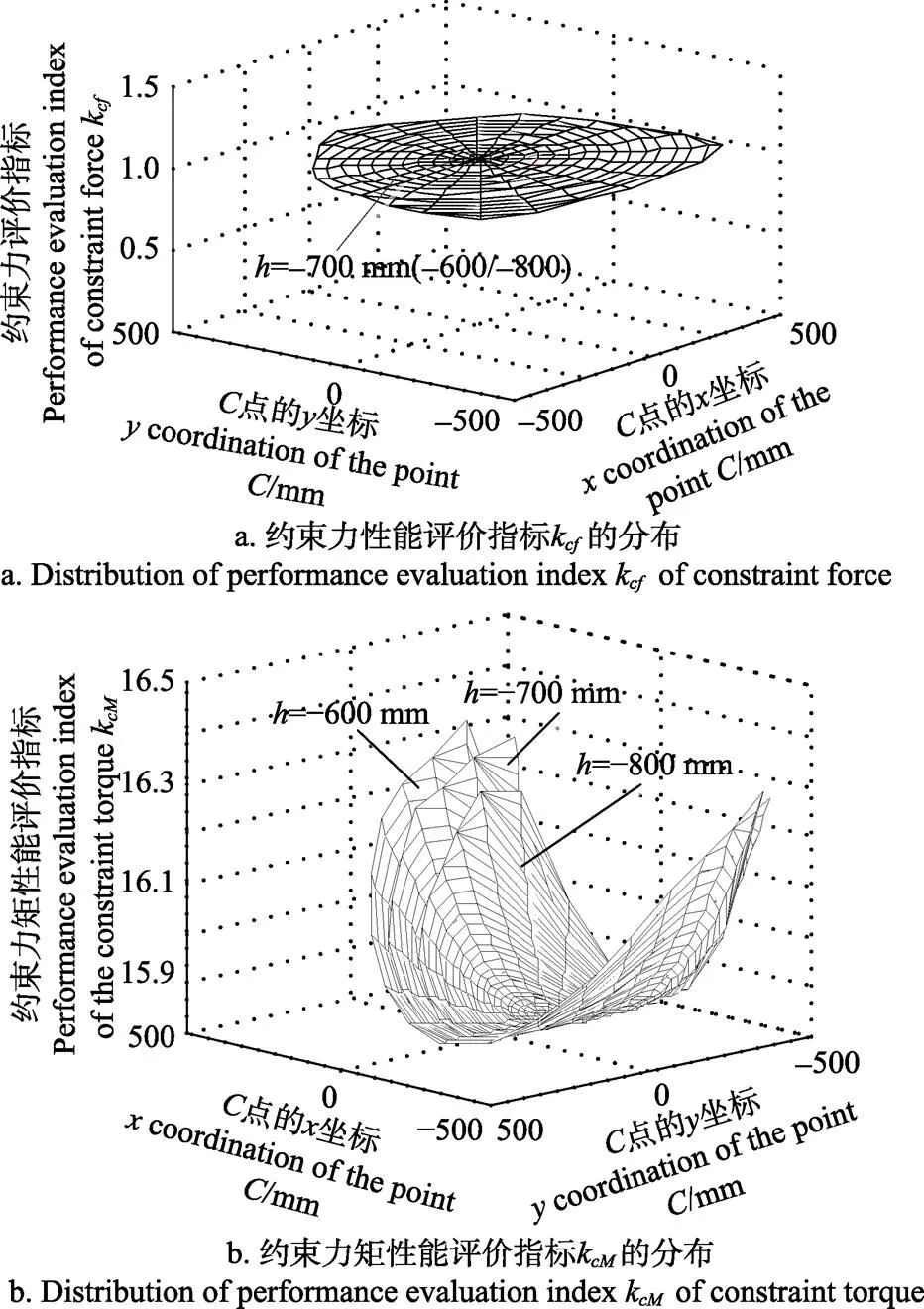
图6 当足端点C的纵坐标为h时约束力和约束力矩性能评价指标kcf和kcM分布
4 腿部机构几何参数设计
腿部机构几何参数设计是集运动、承载、工艺性等多方面的综合设计,而且在设计过程中,各项指标之间相互耦合、相互制约,因此不可能使上述各方面性能同时达到最优。文中所给初选参数是考虑机器人总体设计要求和驱动工作空间优化结果[21]提出的,由图2、图5和图6中的计算结果可知:腿部机构在初选参数下,各项性能值分布较为合理,能够满足腿部机构的设计要求。因此,为了确保腿部机构拥有较大的驱动工作空间,本文将驱动机构的初选参数作为基准参数,以提升腿部机构运动学、静力学性能为目标,对该腿部行走机构中的平行四边形铰链长连杆长6、连接杆长和地面接触连杆长7进行优选。
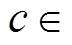
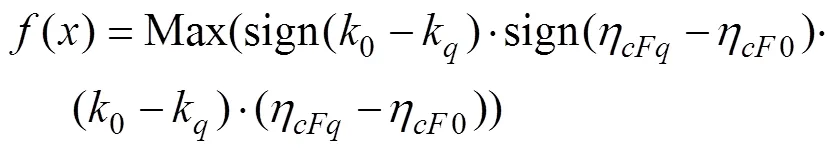
式中0和η0分别为初选参数下该腿部机构的运动学和静力学性能评价指标k和η的值;sign()为符号函数,>0时, sign)=1;否则,sign()=0。
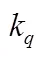
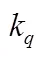
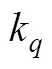
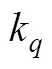
分别设定,6和7的变化步长为10,10和20,基于式(33)提出的优选函数,编写搜索循环程序,最终可得优选参数为(mm):=140,6=330,7=320。分别将优化前后腿部机构几何参数带入式(4)和式(29)中可得k,η和η优化前的值分别为:6.409,3.458和1.990;优化后的值分别为:6.095,4.081和1.864。
由优化前后数据对比可得:优化后该机械腿的k值减小了5.46%,η值增大了18.02%,η值减小了6.33%;由此可得该六足机器人腿部机构的运动学和静力学传递性能得到了改善。

图8 优化前后足端点的额定摩擦系数μe沿y轴的分布图
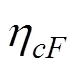
综上可得,该腿部机构的最终几何参数(mm)为:=276,1=70,=55,1=2=220,3=250,33=120,1=2=200,3=200,=140,4=5=200,6=330,7=320,l=190,l=55,g=46.5。基于该腿部几何参数和机器人整体设计要求,与上海交通大学联合开发的六足机器人,如图9所示,图中为该机器人参加某大型展会时的行走(以三角步态行走)演示图。
图9 六足机器人行走演示
Fig.9 Walking demonstration of the hexapod robot
5 结 论
本文针对三自由度六足腿式机器人并联驱动机械腿的实际作业工况定义了多项运动学静力学性能指标,并以其为目标对该机械腿进行了综合性能评价与优化设计。
1)建立了腿部机构在软、硬两种地面下的驱动力与足端力/力矩的映射模型,基于线性空间理论建立了并联驱动机构约束雅可比矩阵。定义了腿部机构运动学及静力学性能指标,通过对各项指标进行定量分析可得:当行走机构所在平面与RU支链所在平面重合时,腿部机构的综合性能较好,因此该平面更适合作为腿机构的主运动平面;且由于该腿部机构在1轴正向区域比1轴负向区域的运动及静力学性能好,1轴正向更适合作为腿部机构前进的方向。
2)基于全域运动学及静力学性能指标,对该腿部机构进行多目标几何参数优选,优选结果表明:杆件11、3和12(见图1)的几何参数为220、250和110 mm,杆件12、1和5的几何参数为330、140和320 mm时,腿部机构综合性能较好,具体表现为运动性能提升5.46%,重力方向最大承载力提升18.02%,驱动关节的最大扭矩减小了6.33%。基于优选几何参数研制了六足机器人样机。所研究的结果为该六足机器人的步态规划及控制提供理论基础。
[1] 师丽娟. 中外农业工程学科发展比较研究[D]. 北京:中国农业大学,2016. Shi Lijuan. Comparative Study of Agricultural Engineering Discipline in China and Some Developed Countries[D]. Beijing: China Agricultural University, 2016. (in Chinese with English abstract)
[2] 李峰. 我国中部农业循环经济发展战略研究[D]. 长沙:武汉大学,2013. Li Feng. Research on the Agricultural Circular Economy Development Strategy of Central Region in China[D]. Changsha: Wuhan University, 2013. (in Chinese with English abstract)
[3] 杨邦杰, 裴志远, 周清波, 等. 我国农情遥感监测关键技术研究进展[J]. 农业工程学报,2002,18(3):191-194. Yang Bangjie, Pei Zhiyuan, Zhou Qingbo, et al. Key technologies of crop monitoring using remote sensing at a national scale: Progress and problems[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2002, 18(3): 191-194. (in Chinese with English abstract)
[4] 纪超,冯青春,袁挺,等. 温室黄瓜采摘机器人系统研制及性能分析[J]. 机器人,2011,33(6):726-730. Ji Chao, Feng Qingchun, Yuan Ting, et al. Development and performance analysis on cucumber harvesting robot system in greenhouse[J]. Robot, 2011, 33(6): 726-730. (in Chinese with English abstract)
[5] Kanae T, Tateshi F, Akira A, et al. Cherry-harvesting robot[J]. Compute Electron Agriculture, 2011, 63(1): 65-72.
[6] 张铁中,杨丽,陈兵旗,等. 农业机器人技术研究进展[J]. 中国科学,2010,40(增刊):71-87. Zhang Tiezhong, Yang Li, Chen Bingqi, et al. Research progress of agricultural robot technology[J]. Science China, 2010, 40(Supp.): 71-87. (in Chinese with English abstract)
[7] 田兴华,高峰,陈先宝,等. 四足仿生机器人混联腿构型设计及比较[J]. 机械工程学报,2013,49(6):81-88. Tian Xinghua, Gao Feng, Chen Xianbao, et al. Mechanism design and comparison for quadruped robot with parallel-serial leg[J]. Journal of Mechanical Engineering, 2013, 49(6): 81-88. (in Chinese with English abstract)
[8] Xu Kun, Ding Xilun. Typical gait analysis of a six-legged robot in the context of metamorphic mechanism theory[J]. Chinese Journal of Mechanical Engineering, 2013, 26(4): 771-783.
[9] Pan Yang, Gao Feng. A new six-parallel-legged walking robot for drilling holes on the fuselage[J]. Journal Mechanical Engineering Science, 2014, 228(4): 753-764.
[10] 杨龙,周玉林,马秋明. 新型球面并联人形机器人踝关节机构静力学性能分析[J]. 中国机械工程,2017,28(7):835-841. Yang Long, Zhou Yulin, Ma Qiuming. Static property analyses of a novel spherical parallel humanoid robotic ankle mechanism[J]. China Mechanical Engineering, 2017, 28(7): 835-841. (in Chinese with English abstract)
[11] 汪满新,刘海涛,黄田. 3-SPR并联机构运动性能评价[J]. 机械工程学报,2017,53(5):108-115. Wang Manxin, Liu Haitao, Huang Tian. Kinematics performance evaluation of a 3-SPR parallel manipulator[J]. Journal of Mechanical Engineering, 2017, 53(5): 108-115. (in Chinese with English abstract)
[12] 李剑锋,李世才,陶春静,等. 并联2-UPS/RRR踝关节康复机构及运动性能分析[J]. 机器人,2016,38(2):143-144. Li Jianfeng, Li Shicai, Tao Chunjing, et al. Parallel 2-UPS/RRR ankle rehabilitation mechanism and kinematic performance analysis[J]. Robot, 2016, 38(2): 143-144. (in Chinese with English abstract)
[13] 曲海波,梁艺瀚,方跃法,等. 4-RRS冗余球面并联机构的静力学与刚度分析[J]. 机械工程学报,2015,51(11):8-15. Qu Haibo, Liang Yihan, Fang Yuefa. et al. Statics and stiffness analysis of 4-RRS redundant spherical parallel mechanism[J]. Journal of Mechanical Engineering, 2015, 51(11): 8-15. (in Chinese with English abstract)
[14] 崔国华,张海强,徐丰,等. 空间3-PUS-UP并联机构运动灵巧性与刚度性能研究[J]. 农业工程学报,2014,45(12):348-354. Cui Guohua, Zhang Haiqiang, Xu Feng, et al. Kinematic dexterity and stiffness performance of spatial 3-PUS-UP parallel manipulator[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 45(12): 348-354. (in Chinese with English abstract)
[15] 荣誉,金振林,曲梦可.三自由度并联机械腿静力学分析与优化[J]. 农业工程学报,2012,28(20):41-49. Rong Yu, Jin Zhenlin, Qu Mengke. Statics analysis and optimal design of 3-DOF parallel mechanical leg[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2012, 28(20): 41-49. (In Chinese with English abstract)
[16] 张东胜,许允斗,侯照伟, 等. 五自由度混联机器人优化设计与运动学分析[J]. 农业工程学报,2016,32(24):69-76. Zhang Dongsheng, Xu Yundou, Hou Zhaowei, et al. Optimal design and kinematics analysis of 5-DOF hybrid serial- parallel manipulator[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(24): 69-76. (in Chinese with English abstract)
[17] Pan Yang, Gao Feng. Kinematic performance analysis for hexapod robot using parallel mechanism[C]//Proceedings of the ASME 2014 International Design Engineering Technical Conferences &Computers and Information in Engineering Conference, 2014: 1-9.
[18] 金波, 陈诚, 李伟. 基于能耗优化的六足步行机器人力矩分配[J]. 浙江大学学报,2012,46(7):1168-1174. Jin Bo, Chen Cheng, Li Wei. Optimization energy-efficient torque distribution for hexapod walking robot[J]. Journal of Zhejiang University, 2012, 46(7): 1168-1174. (in Chinese with English abstract)
[19] 崔冰艳. 仿生机器人并联关节/运动单元的性能分析与设计[D]. 秦皇岛:燕山大学,2011. Cui Bingyan. Performance Analysis and Design for Parallel Joint/Kinematical Unit of Bionic Robot[D]. Qinhuangdao: Yanshan University, 2011. (in Chinese with English abstract)
[20] 张金柱, 金振林, 陈广广. 六足步行机器人腿部机构运动学分析[J]. 农业工程学报,2016,32(9):45-52. Zhang Jinzhu, Jin Zhenlin, Chen Guangguang. Kinematic analysis of leg mechanism of six-legged walking Robot[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(9): 45-52. (in Chinese with English abstract)
[21] 金振林,张金柱,高峰. 六足消防机器人及其腿部机构运动学分析[J]. 中国机械工程,2016,27(7):865-871. Jin Zhenlin, Zhang Jinzhu, Gao Feng. A firefighting six-legged robot and its kinematics analysis of leg mechanism[J]. China Mechanical Engineering, 2016, 27(7): 865-871. (in Chinese with English abstract)
[22] 李满宏, 张建华, 张明路. 新型仿生六足机器人自由步态中足端轨迹规划[J]. 中国机械工程,2014,25(6): 821-825. Li Manhong, Zhang Jianhua, Zhang Minglu. Foot trajectory planning for a hexapod biomimetic robot using free gait[J]. China Mechanical Engineering, 2014, 25(6): 821-825. (in Chinese with English abstract)
[23] Pan Yang, Gao Feng, Qi Chenkun, et al. Human-tracking strategies for a six-legged rescue robot based on distance and view[J]. Chinese Journal of Mechanical Engineering, 2016, 29(2): 219-230.
[24] Pan Yang, Gao Feng. Position model computational complexity of walking robot with different parallel leg mechanism topology patterns[J]. Mechanism and Machine Theory, 2017, 107: 324-337
[25] 刘海涛. 少自由度机器人机构一体化建模理论、方法及工程应用[D]. 天津:天津大学,2010. Liu Haitao. Unified Parameter Modeling of Lower Mobility Robotic Manipulators: Theory, Methodology and Application[D]. Tianjin: Tianjin University, 2010. (in Chinese with English abstract)
[26] Chen Fu, Zang Xizhe, Yan Jihong, et al. Development of navigable hexapod biomimetic robot spider [J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(3): 765-770.
[27] Gang Chen, Bo Jin, Ying Chen. Tripod gait-based turning gait of a six-legged walking robot[J]. Journal of Mechanical Science and Technology, 2017, 31(3): 1401-1411.
[28] Gulalkari A V, Pratama P S, Hoang G, et al. Object tracking and following six-legged robot system using Kinect camera based on Kalman filter and backstepping controller[J]. Journal of Mechanical Science and Technology, 2015, 29(12): 542-543.
[29] 郭孔辉, 庄晔, CHEN Shih-Ken, 等. 轮胎胎面橡胶-冰面摩擦试验方法研究[J]. 摩擦学学报,2005,25(3):234-237. Guo Konghui, Zhuang Ye, CHEN Shih-Ken, et al. Study of the test method to determine rubber-Icy road friction[J]. Tribology, 2005, 25(3): 234-237. (in Chinese with English abstract)
[30] 许美君,李黎,高鑫鑫,等. 纹理方向对木材与橡胶带间摩擦系数的影响[J]. 木材加工机械,2012,5:38-42. Xu Meijun, Li Li, Gao Xinxin, et al. Grain direction influencing on the friction coefficient between wood and rubber belts[J]. Wood Processing Machinery, 2012, 5: 38-42. (in Chinese with English abstract)
张金柱,金振林,张天浩.并联驱动机械腿运动学静力学性能评价及几何参数设计[J]. 农业工程学报,2017,33(21):61-69. doi:10.11975/j.issn.1002-6819.2017.21.007 http://www.tcsae.org
Zhang Jinzhu, Jin Zhenlin, Zhang Tianhao. Kinematic/static performance evaluation and geometric parameter design of parallel-driving leg mechanism[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(21): 61-69. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2017.21.007 http://www.tcsae.org
Kinematic/static performance evaluation and geometric parameter design of parallel-driving leg mechanism
Zhang Jinzhu, Jin Zhenlin※, Zhang Tianhao
(066004,)
In order to raise mechanization and automation level of agricultural operations, broaden the scope of application of agricultural robot, a novel three degree of freedom leg mechanism used in the six-legged walking robot was introduced. The kinematic and static performances of the leg mechanism were analyzed. The geometric parameters of the leg mechanism were optimized by multiple objectives. In this paper, firstly, the coupling relationship between the linear velocity and angular velocity of the foot was resolved. The kinematic performance index was defined based on the condition number of Jacobian matrix. The distribution diagram of kinematic performance indexwas drawn. It can be seen that kinematic performance index was small in the central area of workspace of the leg mechanism from this distribution diagram. It was shown that the kinematic performance of leg mechanism was better in the central area than other areas of workspace of the leg mechanism. Secondly, the ground surface types were summarized as hard and soft ground surfaces considering the acting generalized force types between the standing foot and the ground surface. The acting generalized forces were three-dimensional pure force when the ground surface type was hard ground. The acting generalized forces were six-dimensional force when the ground surface type was soft ground. The driving static model of the whole leg mechanism was built based on the principle of virtual work. Then according to different ground surface, the local and global static performance evaluation indices were proposed. The distribution diagrams of the local static performance evaluation indices were drawn, respectively. It can be seen that the load performance was batter in the area of>0 than the one in the area of<0 (as shown in Fig.1).Again the closer to the boundary of workspace the leg was, the better the static transfer performance of the leg mechanism was. But, the leg mechanism needed more rough ground to provide enough friction when the standing leg was in the boundary of its workspace. The constraint Jacobian matrix of the driving mechanism was built based on the theory of linear space. The constraint statics performance evaluation indices were proposed based on constraint Jacobian matrix. The distribution diagram of the local constraint statics performance indexwas drawn. From the distribution diagram, it can be seen that constraint force transfer performance index remained unchanged in everywhere of the workspace and constraint torque transfer performance index was smaller in the area of=0 than other areas. It was shown that constraint force transfer performance of driving mechanism was good and constant in whole workspace, constraint torque transfer performance of driving mechanism was better in the area of=0. Lastly, aiming at improving comprehensive property of leg mechanism, its geometric parameters were optimized using searching method. Optimization results showed that when the parameters of the long rod and connecting rod of parallelogram mechanism was 330 mm and 140 mm, respectively, the parameters of rod connected with ground was 320 mm, comprehensive property of leg mechanism was better. Compared with before optimization, the kinematic performance of the optimized leg mechanism was increased by 5.46%, the maximum gravity load was increased by 18.02%, and the maximum torque of the driving joint was reduced by 6.33%. The hexapod robot was designed based on optimized parameters. The research results provide a theoretical basis for the gait planning and control of the six legged robot. Meanwhile, optimal design method for geometric parameters of leg mechanism of the six-legged robot applied in this paper is also applicable to other six legged robot.
robots; kinematics; static analysis; parallel-driving mechanical leg; performance evaluation; parameter design
10.11975/j.issn.1002-6819.2017.21.007
TP242
A
1002-6819(2017)-21-0061-09
2017-05-16
2017-09-01
国家重点基础研究发展计划(973计划)资助项目(2013CB035501)机械系统与振动国家重点实验室课题资助项目(MSV201506);河北省研究生创新资助项目(2016SJBS011)
张金柱,男,博士生,主要研究方向为多足步行机器人技术及其应用。Email:ysuzhangjz@126.com
※通信作者:金振林,男,教授、博士研究生导师,主要研究方向为并联机器人技术及应用。Email:zljin@ysu.edu.cn

