关于通信结点连接问题的优化模型∗

桂改花

（广东科学技术职业学院 珠海 519090）

关于通信结点连接问题的优化模型∗

桂改花

（广东科学技术职业学院 珠海 519090）

论文运用Kruskal算法，求出通信网络的最小化连接成本。出于安全可靠性考虑，要求网络中除某固定的两个结点外，其它任意三个结点被破坏时，仍然能够保持这两个结点之间的通信，论文用LINGO程序遍历出最优解，论文还用Matlab软件，以穷举法为核心，以Dijkstra迪克斯特拉算法和0-1规划作为辅助，编写程序，尽可能地遍历所有的可能解，最终得出的结果与用LINGO软件得出的结果一致，充分证明了答案的准确性。

最小生成树；Kruskal算法；穷举法；0-1规划

1 引言

结点是指一台电脑或其他设备与一个有独立地址和具有传送或接收数据功能的网络相连。结点可以是工作站、客户、网络用户或个人计算机，还可以是服务器、打印机和其他网络连接的设备。每一个工作站、服务器、终端设备、网络设备，即拥有自己唯一网络地址的设备都是网络结点［1］。整个网络就是由这许许多多的网络结点组成的，把许多的网络结点用通信线路连接起来，形成一定的几何关系，这就是计算机网络拓扑［2］。

通信网络［3］结构也是计算机网络拓扑中在实际中的一个应用，通信网络的网络终端之间都是由电缆连接的，求解一个通讯网络的最小连接成本其实就是最优连线问题，又称最小生成树［4］问题，是求网络中长度最小的生成树。对于最小生成树问题，可采用“避圈法”的推广，Kruskal算法［5］。出于安全可靠性［6］考虑，要求网络中除某固定的两个结点外，其它任意三个结点被破坏时，仍然能够保持这两个结点之间的通信，本文用LINGO［7］程序遍历出最优解，存在局部最优解的可能，因此，本文用Matlab［8］软件，以穷举法［9］为核心，以迪克斯特拉（Dijkstra）算法［10］和0-1规划［11］作为辅助，编写程序，尽可能地遍历所有的可能解，最终得出的结果与用LINGO软件得出的结果一致，充分证明了答案的准确性。给出连接方案。

2 算法简介

2.1 Kruskal算法

第1步 选e1∈T；

第2步 考虑e2，如果e2加入T不会产生回路，则把e2加入T，否则放弃e2；再考虑e3，如果e3加入T不会产生回路，则把e3加入T，否则放弃e3；如此反复下去，直到无边可选为止。这样选出的T就是赋权图G的最小生成树。

2.2 求最短路的算法-迪克斯特拉（E.W.Dijkstra）算法

基本思想：把图中所有点分为两组，第一组包含已确定最短路径的结点，第二组包含尚未确定最短路径的结点。然后把第二组的点逐个加到第一组中去，直到从某点出发可以到达的所有点都包含在第一组中。

计算赋权图中各对顶点之间最短路径，显然可以调用Dijkstra算法。具体方法是：每次以不同的顶点作为起点，用Dijkstra算法求出从该起点到其余顶点的最短路径，反复执行次这样的操作，就可得到从每一个顶点到其它顶点的最短路径。

3 案例分析

图1是一个拟建的通信网络，11个小圆圈代表网络终端结点，终端结点通过地下电缆双向连接，以进行数据传输；结点间的数字表示距离，单位：km。

1）终端间的连接方案，以最小化总连接成本；

2）出于安全可靠性考虑，除10、11结点外，其它任意三个结点被破坏时，仍然能够保持结点10和11之间的通信，给出连接方案。

图1 通信网络图

3.1 问题一：求解

按照上文的表达式，写出相应的LINGO程序，根据输出结果，画出连接图，如下：

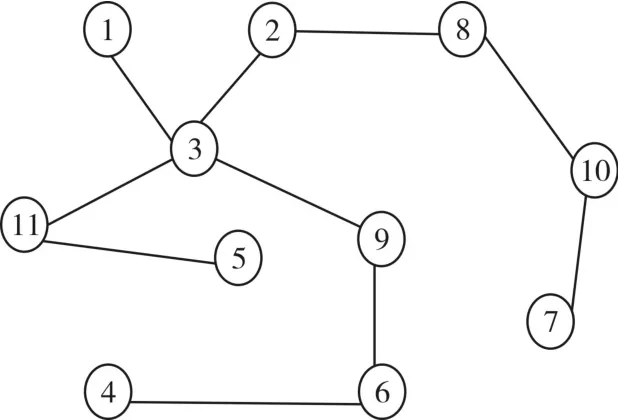
图2 LINGO结果1连接图

3.2 问题二：建模过程

3.2.1 LINGO方法程序思路

网络中除10、11结点外，其它任意三个结点被破坏时，仍然能够保持结点10和11之间的通信，则网络中至少存在4条通路，才能保证连通10、11两点，且11只出，10只进，对于任意两点的通路进行标记，有通过的标为1，否则为0，为确保10、11连通，就必须保证1到9中每个点进路和出路都至少为1，最后算总路径：所有有经过的路之和。

3.2.2 LINGO程序结果

依据程序思路，写出LINGO程序的约束条件，依据结果，画出最优的连接方案：

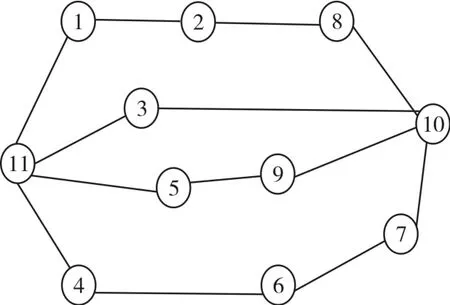
图3 LINGO程序结果2连接图

3.2.3 Matlab方法程序思路N-S图

图4 N-S图

3.2.4 Matlab方法程序思路流程图

图5 流程图

3.2.5 Matlab程序结果

将以上程序思路转化为Matlab代码，运行结果如下：

11→1；11→3；11→5；114；1→4；310；5→9；46；2→8；910；67；810；710；

结果与用LINGO得出的结果一致，总路径均为2347，成功验证了LINGO方法。

4 结语

本模型由于分别采用了LINGO和Matlab两种方法，避免了由于主观意识所导致的结果不准确，程序分别得出了一致的结果，证明方法的正确性。

由于本模型中采用Matlab方法的程序并未涉及太多对于该问题的局限性，因此对于其他网络结点问题，只要代入相应数据并修改部分代码，可实现该模型推广的可能，对于降低工程建设的成本有很大的帮助。

［1］李全岗，刘峤，秦志光.基于主体模型的通信网络建模与仿真［J］.计算机研究与发展，2016，53（1）：206-215.LI Quangang，LIU Qiao，QIN Zhiguang.Modeling and Simulation Network Based on Topic Model［J］.Journal of Computer Research and Development，2016，53（1）：206-215.

［2］包学才，戴伏生，韩卫占.基于拓扑的不相交路径抗毁性评估方法［J］.系统工程与电子技术，2012，34（1）：168-174.BAO Xuecai，DAI Fusheng，HAN Weizhan.Evaluation method of network invulnerability based on disjoint paths in topology［J］.Systems Engineering and Electronics，2012，34（1）：168-174.

［3］余新，李艳和，郑小平，等.基于网络性能变化梯度的通信网络节点重要程度评价方法［J］.清华大学学报（自然科学版），2008，48（4）：541-544.YU Xin，LI Yanhe，ZHENG Xiaoping，et al.Node importance evaluation based on communication network performance grads［J］.Tsinghua Univ（Sci&Tech），2008，48（4）：541-544.

［4］孙小军，刘三阳，王志强.一种求解最小生成树问题的算法［J］.计算机工程，2011，37（23）：241-243.SUN Xiaojun，LIU Sanyang，WANG Zhiqiang.Algorithm for Solving Minimum Spanning Tree Problem［J］.Computer Engineering，2011，37（23）：241-243.

［5］司守奎，孙兆亮.数学建模算法与应用［M］.北京：国防工业出版社，2015.48-49.SI Shoukui，SUN Zhaoliang.MathematicalModeling Algorithms and Application［M］.Beijing：National Defense Industry Press，2015.48-49.

［6］刘普寅，张维明.通信网络可靠性研究中的数学问题［J］.通信学报，2000，21（10）：50-57.LIU Puyin，ZHANG Weiming.Mathematical problems in research on reliability of communication networks［J］.Journal of China Institute of communications，2000，21（10）：50-57.

［7］谢金星，薛毅.优化建模与LINDO/LINGO软件［M］.北京：清华大学出版社，2005.XIE Jinxing，XUE Yi.Optimization Modeling and LINDO/LINGO［M］.Beijing：Tsinghua University Press，2005.

［8］卓金武，李必文，魏永生，等.MATLAB在数学建模中的应用［M］.北京：北京航空航天大学出版社，2014.ZHUO Jinwu，LI Biwen，WEI Yongsheng，et al.Application of MATLAB in Mathematical Modeling［M］.Beijing：Beijing University of Aeronautics and Astronautics press，2014.

［9］孙义欣，冯娜.穷举法在程序设计中的应用［J］.计算机时代，2012，8：50-52.SUN Yixin，FENG Na.Application of exhaustion method in programming［J］.Computer Era，2012，8：50-52.

［10］司守奎，孙兆亮.数学建模算法与应用［M］.北京：国防工业出版社，2015.40-44.SI Shoukui，SUN Zhaoliang.MathematicalModeling Algorithms and Application［M］.Beijing：National Defense Industry Press，2015.40-44.

［11］张玉兰，曹亚萍.基于0-1规划的高校选课策略［J］.高师理科学刊，2014，34（6）：14-15.ZHANG Yulan，CAO Yaping.Strategy of college course selection based on 0-1planning［J］.Journal of Science of Teachers'College and University，2014，34（6）：14-15.

Optimization Model For Communications Node Connection Problem

GUI Gaihua
（Guangdong Institute of Science，Zhuhai 519090）

This paper uses Kruskal algorithm to get the communication network connection cost minimization.For the sake of safety and reliability，requirements in addition to a fixed two nodes in the network，any other three nodes are destroyed，it will still be able to keep this communication between two nodes.In this paper，LINGO program is used to traversal the optimal solution.This article also use the Matlab software，using exhaustive method as the core，to terra dix Dijkstra algorithm and 0-1 programming as auxiliary and write a program，as far as possible to iterate through all possible solutions.Final results are consistent with the results using LINGO software，fully proved the accuracy of the answers.

minimum spanning tree，Kruskal algorithm，exhaustive method，0-1 programming

TP391

10.3969/j.issn.1672-9722.2017.10.002

Class Number TP391

2017年4月10日，

2017年5月20日

广东省高职教育一类品牌专业资助项目（编号：2016gzpp007）资助。

桂改花，女，硕士研究生，讲师，研究方向：应用数学。