适用于BOC(m,n)信号的无模糊捕获技术

张洪伦， 巴晓辉， 陈杰,*， 周航

1.中国科学院微电子研究所， 北京 100029

2.中国科学院大学， 北京 100049

适用于BOC(m,n)信号的无模糊捕获技术

张洪伦1, 2， 巴晓辉1， 陈杰1,*， 周航1

1.中国科学院微电子研究所， 北京 100029

2.中国科学院大学， 北京 100049

针对二进制偏移载波(BOC)调制信号自相关多峰特性引起的信号捕获模糊性问题，提出了一种子相关相乘边峰消除技术(CMSCT)。根据BOC子相关函数的特性，通过将不同子相关函数相乘获得边峰消除能力，并且为了充分利用接收信号，进一步提高捕获性能，提出了相应的优化算法。分析对比了提出算法的实现复杂度和基于恒虚警率准则的峰值发现概率，对Galileo E1C中频采样信号的处理结果表明:提出的边峰消除方法有效解决了捕获模糊性问题。

全球导航卫星系统； 二进制偏移载波调制； 无模糊捕获； 相关函数； 边峰消除

随着卫星导航系统应用的不断推广及深入，用户对定位精度和可靠性提出了更高的要求，因此现代化的全球导航卫星系统(Global Navigation Satellite System，GNSS)增加了许多新的信号[1-5]，不同卫星导航系统及同一导航系统在相同频带上可能会发送多路信号，为了加强新增信号与现存信号的兼容性，减小卫星导航系统间与系统内信号之间的干扰，引入二进制偏移载波(Binary Offset Carrier,BOC)调制技术，利用其谱分裂性质，将BOC调制信号能量搬离中心频带。但是BOC调制信号自相关函数具有多峰特性，信号可能会错误地同步到边峰上，造成捕获模糊性问题[6]。

为了解决捕获模糊性问题，已经提出了很多方案，按照不同的分析方法，大体可以分为频域处理方案和时域处理方案[7]。比较典型的频域解决方案为边带处理技术[8-10]，将接收到的BOC信号看成两个二进制相移键控(Binary Phase Shift Keying，BPSK)信号的叠加，其载波频率分别对称地置于BOC信号载波频率的两边，每一个边带都可以看成独立的BPSK信号，可以完全消除模糊性问题。但是边带技术需要对信号进行滤波等处理，复杂度增加，文献[11]提出了简化方案，性能损失0～2.5 dB。文献[12]使用简化的滤波器对相关结果进行滤波，也可获得边峰消除能力。频域处理方案通常会获得较宽的相关峰，可以设置较大的码相位搜索步长，减少捕获时间，但是捕获码相位精度不高，在跟踪初始阶段需要额外处理才能进入稳定锁定状态。

近年来，针对捕获模糊性问题，时域处理方案受到广泛关注，成为研究热点。较早提出的ASPeCT算法[13]有效抑制了BOC自相关边峰，但只适用于正弦相控BOC(n,n)信号的捕获和跟踪。文献[14]给出一种适用于BOC(m,n)信号捕获方法，对BOC(m,n)与本地扩频码的互相关结果求导，再与互相关基准序列进行相关，通过峰值检测完成信号捕获，但是其在求导、与互相关基准序列进行相关时需要大量额外运算。GRASS (General Removing Ambiguity via Sidepeak Suppressing)技术[15]通过额外设计一种本地辅助信号，与接收的BOC信号进行互相关运算，结合BOC自相关给出一种新的检验统计量，能够有效压制边峰对信号捕获的影响，文献[16]对其进行推广，但是GRASS技术引入一个乘积因子α，对于高阶BOC调制信号，α放大了噪声的影响。文献[17]也是通过构造本地辅助信号的方式获得边峰消除能力，但只适用于高阶BOC信号。文献[18]提出无模糊同步方案，需要设计两个本地辅助信号，但是辅助信号脉冲宽度选择不够灵活。CCART (Correlation Combination Ambiguity Removing Technology)[19]从信号分解的角度，将接收BOC信号分解为若干周期矩形脉冲信号，分别与本地BOC信号和相应扩频码进行相关运算，最后通过组合处理去除边峰，但是接收信号的扩频码相位及码多普勒信息都未知，不可能对接收BOC信号进行分解，只有当码多普勒较小、每个矩形脉冲只进行单点采样时，才能够实现，所以这种方案不可能在实际中应用。

本文通过对BOC信号进行分解，提出一种适用于BOC信号无模糊捕获的相关相乘边峰消除技术(Correlation Multiplication Side-peak Cancellation Technique,CMSCT)，为了进一步提高捕获性能，对提出的算法进行了优化。

1 BOC(m,n)信号无模糊捕获原理

1.1 信号模型

BOC信号分为正弦相控BOC(sine-phased BOC，sBOC)信号和余弦相控BOC(cosine-phased BOC，cBOC)信号，基带信号可表示为

ssBOC(t)=c(t)sign[sin(2πfsubt)]

(1)

scBOC(t)=c(t)sign[cos(2πfsubt)]

(2)

式中：c(t)为扩频码；sign[·]为符号函数；fsub为子载波频率。sBOC/cBOC统称BOC(fsub,fc)，其中fsub=m×1.023 MHz，fc=n×1.023 MHz，简记为BOC(m,n)，N=2m/n为BOC调制阶数。除特别说明，均以sBOC(kn,n)为例进行分析。

定义矩形脉冲信号pi(t)为

(3)

式中：i=0,1,…,N-1；Tc=1/fc为一个扩频码片长度。则sBOC(m,n)基带信号表示为

(4)

1.2 相关特性

假设扩频码序列自相关特性理想，相干累加时间为Tcoh，则BOC归一化自相关函数Rboc(τ)在|τ|>Tc时取0。扩频码如图1(a)所示，当|τ|≤Tc时扩频码有重叠，相关积分不为0，并且每个码片重叠部分的相关积分结果相同。当-Tc<τ≤0时，Rboc(τ)如式(5)所示，当0<τ≤Tc时仍得到相同结果。

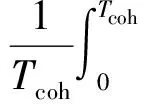
(5)

式中：

Rboc,i(τ)=

(6)

其中：Rboc,i(τ)在[0,Tc]或[-τ,Tc]上积分相同。

式(4)可写为

(7)

式中：

(8)

因此sBOC(m,n)信号可分解为N个子信号sboc,i(t)，i=0,1,…,N-1，每个子信号sboc,i(t)表示sBOC(m,n)信号的每个扩频码片内第i个矩形脉冲保留，其他置0。图1(b)以sBOC(2,1)为例，将其分解为4个子信号。

图1 扩频码、sBOC(2,1)调制信号及其子信号波形
Fig.1 Spreading code, sBOC(2,1) modulation signal and its decompositions

根据式(6)～式(8)，Rboc,i(τ)可进一步表示为

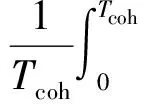
(9)

式中：i=0,1,…,N-1。因此Rboc,i(τ)可以表示为sBOC(m,n)信号与其子信号sboc,i(t)的互相关，称为子相关函数(sub-correlation function)，而sBOC(m,n)自相关函数等价于所有子相关函数Rboc,i(τ)之和，如式(5)所示。

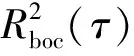
图2为sBOC(2,1)自相关及其子相关函数，每个子相关结果由4个三角形脉冲叠加而成，所有子相关函数之和等于sBOC(2,1)自相关函数。

图2 sBOC(2,1)自相关及其子相关函数
Fig.2 Auto-correlation and sub-correlation functions of sBOC(2,1)

图3 用于sBOC(2,1)的CMSCT
Fig.3 CMSCT for sBOC(2,1)

1.3 相关相乘边峰消除技术

由图2给出的子相关函数，将Rboc,0(τ)和Rboc,3(τ)相乘，结果只剩下一个正的主峰和两个负边峰，如图3所示，子相关函数已归一化，而负边峰对捕获没有影响。对于所有sBOC(m,n)信号都会得到相同的结果，将本地BOC信号按式(7)进行分解，分别与接收信号进行相关运算，最后根据式(10)得到构造函数Rsct(τ)，可用于无模糊捕获，将这种边峰消除方法简记为CMSCT：

Rsct(τ)=Rboc,0(τ)·Rboc,N-1(τ)

(10)

1.4 优化算法

由式(10)给出的CMSCT，有效消除了BOC自相关边峰对信号捕获的影响，但是当k>1时，该方法只利用了部分接收信号，导致扩频增益降低。为了充分利用所有接收信号，减少扩频增益损失，在k>1时，基于CMSCT提出了两种算法优化策略。

1.4.1 优化算法1 (CMSCT 1)

基于CMSCT及文献[19]提出的CCART，给出一种优化算法(CMSCT 1)。在图2中，令Rboc,0(τ)、Rboc,1(τ)乘积为Rsct,1(τ)，Rboc,2(τ)、Rboc,3(τ)的乘积为Rsct,2(τ)，可以得到Rsct,1(τ)与Rsct,2(τ)关于原点对称，经过式(11)处理得到Ralg1(τ)，消除所有正边峰，可用于信号捕获，如图4 所示。

Ralg1(τ)=Rsct,1(τ)+Rsct,2(τ)-

|Rsct,1(τ)-Rsct,2(τ)|

(11)

对于任意k>1的sBOC(kn,n)信号，都可以使用类似方法消除正边峰，具体如下：

1) 计算所有2k个子相关Rboc,i(τ)。

2) 将子相关分为两组：{Rboc,i(τ),i=0,1,…,k-1}，{Rboc,i(τ),i=k,k+1,…,2k-1}，第1组用Rboc,0(τ)分别与另外k-1个子相关相乘，第2组用Rboc,2k-1(τ)与另外k-1个子相关相乘：

Rsct,i(τ)=

(12)

很容易推出Rsct,i(τ)与Rsct,2k-i-1(τ)关于原点对称，其中i=1,2,…,k-1。

3) 将关于原点对称的Rsct,i(τ)与Rsct,2k-i-1(τ)

图4 用于sBOC(2,1)的CMSCT 1
Fig.4 CMSCT1 for sBOC(2,1)

经过如式(11)处理，然后再将结果累加，可得

|Rsct,i(τ)-Rsct,2k-i-1(τ)|)

(13)

1.4.2 优化算法2 (CMSCT 2)

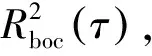
(14)

结合两者的优势，能够得到比CMSCT更好的性能和边峰消除能力。图5为sBOC(2,1)的处理结果。

图5 用于sBOC(2,1)的CMSCT 2
Fig.5 CMSCT 2 for sBOC(2,1)

1.5 算法推广

虽然CMSCT及其优化算法都是假设信号为sBOC(kn,n)调制时提出的，但是同样适用于任意BOC(m,n)调制信号。根据BOC调制阶数和相位可以将其分为4类：① 偶数阶正弦相控BOC调制；② 奇数阶正弦相控BOC调制；③ 偶数阶余弦相控BOC调制；④ 奇数阶余弦相控BOC调制。

sBOC(kn,n)为偶数阶正弦相控BOC调制，对于奇数阶sBOC(m,n)，与sBOC(kn,n)的多峰消除方式基本相同，但是使用CMSCT 1时需要特别注意，因为有奇数个子相关。针对cBOC(m,n)信号，需要将其分解为2N个子BOC信号，此时仍有偶数个子相关，消除多峰的处理方式与sBOC(kn,n)相同。

2 捕获检验统计量分析

2.1 接收信号模型及其相关积分表达式

接收信号模型为

r(t)=Ad(t)sboc(t)cos(2πfrt+θ)+n(t)

(15)

式中：A为信号幅度；d(t)为导航数据；fr为接收信号载波频率；θ服从[0,2π]上均匀分布；n(t)为带限噪声，单边带功率谱密度为N0。信号功率为A2/2，B为2倍的扩频码速率，则信号带宽为2B(包括BOC信号的两个边瓣)，带宽2B内噪声功率σ2=2N0B，信噪比SNR=A2/(4N0B)，载噪比C/N0=A2/(2N0)。

对载波剥离，并对噪声归一化得

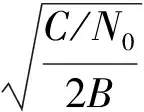
nIp(t)+jnQp(t)

(16)

式中：Δf为频率估计误差；nIp(t)、nQp(t)服从均值为零、方差为1的正态分布。

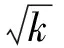
rp(iTs)=Ad(iTs)sboc(iTs)ej(2πΔfiTs+θ)+

nIp(iTs)+jnQp(iTs)

(17)

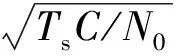
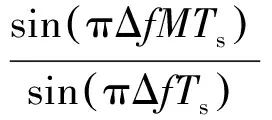
MAdRboc(τ)sinc(πΔfTcoh)ejφm+NI+jNQ

(18)

式中：φm=2πΔfmTcoh+πΔf(M-1)Ts+θ；sinc(x)=sin(x)/x；NI～N(0,M)；NQ～N(0,M)。对噪声归一化得

Xm=A(τ,Δf)ejφm+NI+jNQ=

Im+jQm

(19)

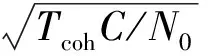
同理，可求得接收信号rp(iTs)与sBOC(m,n)子信号sboc,i(iTs)的噪声归一化互相关积分为

Xi,m=Ai(τ,Δf)dejφi,m+NI(i,m)+jNQ(i,m)=

Ii,m+jQi,m

(20)

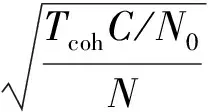
2.2 捕获检验统计量

根据式(19)和式(20)推导出的相关积分结果Xm、Xi,m，能够给出CMSCT及其优化算法的捕获检验统计量。在弱信号情况下，需要更长的数据长度，结合非相干累加进行信号捕获，用L表示非相干累加次数。理论分析时，基于恒虚警率准则设置判决门限，给出相应的峰值发现概率，由于各个算法检验统计量的概率分布函数非常复杂，无法给出判决门限及发现概率的显示表达式，但是当非相干累加次数L较大时，根据中心极限定理，检验统计量近似服从高斯分布。

2.2.1 传统自相关捕获算法及GRASS捕获算法的检验统计量

为了比较分析，给出传统捕获方案的检验统计量：

(21)

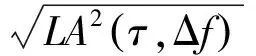
当L=1时，Tboc均值和方差分别为

μboc=E(Tboc)=A2(τ,Δf)+2

(22)

(23)

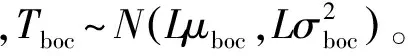
根据以上分析及文献[15]，给出GRASS检验统计量TGRASS均值与方差为

μg=E(TGRASS)=A2(τ,Δf)-2α+2

(24)

(25)

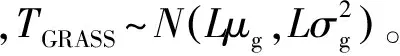
2.2.2 CMSCT检验统计量

CMSCT算法检验统计量为

(26)

由于I0,m、IN-1,m、Q0,m和QN-1,m为相互独立的高斯随机变量，Tsct表示2L个高斯随机变量乘积的累加。

当L=1时，Tsct均值和方差分别为

μsct=E(Tsct)=

A0(τ,Δf)AN-1(τ,Δf)cos(φ0,m-φN-1,m)≈

A0(τ,Δf)AN-1(τ,Δf)

(27)

(28)

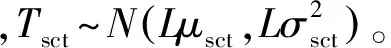
当N=2时，Tsct可以表示为

(29)

式中：第1项表示接收信号与本地BOC(1,1)信号的自相关积分；第2项表示接收信号与本地扩频码互相关积分，与ASPeCT边峰消除技术[13]等价。

2.2.3 优化算法检验统计量

对于优化算法1，根据Tsct，首先给出第m次相关累加后的处理结果Tm,i为

Tm,i=

(30)

最终的CMSCT1检验统计量为

Talg1=

(31)

结合检验统计量Tboc、Tsct的形式，CMSCT2的检验统计量为

(32)

由于Talg1和Talg2的数字特征很难给出，通过仿真给出其性能分析。

2.3 实现复杂度分析

基于CMSCT的捕获算法，需要得到2k个子相关Rboc,i(τ)，最直接地实现方式就是设置2k个相关支路，分别计算子相关，但是计算量和资源消耗都会增加。由于sboc,i(t)对应BOC信号每个码片内第i个矩形脉冲，其他位置为0，因此可以使用一个相关通道，将每个码片的第i个矩形脉冲范围内的相关积分结果累加到Rboc,i(τ)上，从而减少运算量和复杂度。

数据长度和非相干累加次数L相同，BOC自相关及其子相关Rboc,i(τ)已经获得的条件下，不同捕获方法运算量对比如表1所示。与传统算法相比，为了去除多峰影响，各种方法的运算量都会增加。CMSCT 1运算量随着k的增加而增多，其他算法运算量相差不大。

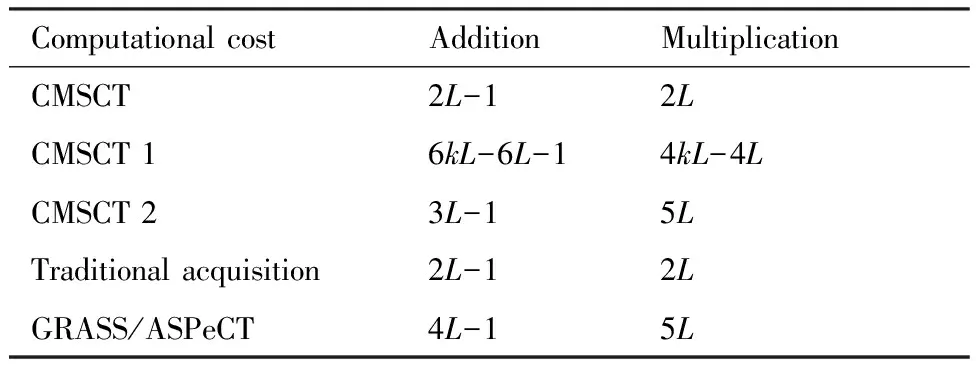
表1 不同捕获方法运算量对比

2.4 性能分析

为了从理论上证明CMSCT的有效性，假设没有码相位与载波频率误差，1 ms相干累加，非相干累加次数L=20，给出恒虚警率Pfa=10-3时峰值发现概率的理论曲线。由于无法给出各个检验统计量的判决门限及发现概率闭合表达式，并且两个CMSCT的优化算法数字特征也未能给出，图6仅给出CMSCT、GRASS及传统捕获方案的近似理论峰值发现概率曲线，应用于sBOC(k,1)，k取1～4。从峰值发现概率角度分析，传统自相关捕获算法的性能最好，GRASS算法性能最差，原因是GRASS在进行边峰压制时引入一个乘积因子，放大了噪声，导致性能恶化。由式(20)及文献[15]，随着BOC调制阶数的增加，两种算法的性能相对传统捕获算法性能随之下降，图6也验证了这一结论，并且当k=1时，CMSCT与GRASS算法等价。这两种算法都是以牺牲性能换取边峰抑制能力，避免由于边峰引起的错误捕获，虽然CMSCT算法只利用了部分信号能量，理论曲线表明其性能仍然高于GRASS算法。

图6 sBOC(k,1)理论峰值发现概率
Fig.6 Theoretical peak probabiliies of detection for sBOC(k,1)

3 实验结果与分析

假设没有码相位与载波频率误差，θ在[0,2π]上服从均匀分布，设置虚警率Pfa=10-3，相干累加1 ms，非相干累加次数L=20，通过Monte Carlo仿真给出CMSCT及其优化算法的峰值发现概率Pd。

图7(a)给出k取值为1～4时CMSCT的理论及仿真结果，可以得到，理论与仿真结果比较吻合。图7(b)～图7(d)分别给出k取值为2～4时，各种算法的峰值发现概率仿真曲线，基于文献[19]的CMSCT 1在k=2时性能低于CMSCT，而CMSCT 2较CMSCT性能有所改善。当k>2时，两种优化算法相对于CMSCT性能都有所改善，CMSCT 2性能更好，随着k的增加，两种优化算法性能差距变小，但是与传统自相关捕获算法相比，性能下降也更多。对于GRASS算法，k越大乘积因子越大，放大了噪声的影响，低于CMSCT算法。

用思博伦信号发生器产生中频数据，采样率16.367 986 MHz，图8为Galileo E1C信号处理结果，数据长度4 ms，L=1，由于载波相位未知，只能给出子相关Rboc,0(τ)、Rboc,1(τ)的平方，捕获检验统计量Tsct不再具有捕获模糊性问题。

图7 sBOC(k,1)仿真峰值发现概率
Fig.7 Simulation peak probabilities of detection for sBOC(k,1)

图8 基于CMSCT的Galileo E1C信号捕获
Fig.8 Acquisition of Galileo E1C signals by CMSCT

CMSCT及其优化算法在牺牲一定性能的情况下，能够有效去除自相关多峰对捕获的影响。当k=1时，CMSCT运算量与ASePCT相比更小，当k>1时，CMSCT 2性能优于GRASS及基于文献[19]给出的CMSCT 1。

4 结 论

1) 提出的CMSCT能够有效解决BOC信号捕获模糊性问题，适用于各种BOC调制信号。将CMSCT应用于Galileo E1C信号捕获，结果表明其能够去除边峰对捕获的影响。

2) 为了进一步提高性能，减少扩频增益损失，提出优化算法CMSCT 1、CMSCT 2。理论分析和仿真实验表明，CMSCT 2的性能优于GRASS算法和CMSCT 1，并且实现复杂度低。

下一步工作，将研究CMSCT在BOC信号跟踪中的应用。

[1] TANG Z P, ZHOU H W, WEI J L, et al. TD-AltBOC: A new COMPASS B2 modulation[J]. Science China Physics, Mechanics and Astronomy, 2011, 54(6): 1014-1021.

[2] 朱建良, 王兴全, 薄煜明, 等. 提高北斗BOC信号捕获精度的伪码相位估计法[J]. 中国惯性技术学报, 2014, 22(1): 79-82.

ZHU J L, WANG X Q, BO Y M, et al. Pseudo code phase estimation method for improving BOC signal acquisition accuracy of BeiDou[J]. Journal of Chinese Inertial Technology, 2014, 22(1): 79-82 (in Chinese).

[3] ZHU X F, CHEN X Y, CHEN J F. Simulation of Galileo E1/E5/E6 digital IF signal[J]. Journal of Chinese Inertial Technology, 2012, 20(5): 557-561.

[4] BARKER B C, BETZ J W, CLARK J E, et al. Overview of the GPS M code signal[C]//Proceedings of the 2000 National Technical Meeting of the Institute of Navigation. Anaheim, CA: the Institute of Navigation, 2000: 542-549.

[5] BETZ J W, BLANCO M A, CAHN C R, et al. Description of the L1C Signal[C]//ION GNSS 2006. Fort Worth, TX: the Institute of Navigation, 2006: 2080-2091.

[6] 刘芳, 冯永新. 多峰值信号的伪码相位估计法[J]. 航空学报, 2010, 31(11): 2253-2258.

LIU F, FENG Y X. A pseudo-code phase estimation method based on multi-peak signals[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(11): 2253-2258 (in Chinese).

[7] YAO Z. Unambiguous processing techniques of binary offset carrier modulated signals[M]. Rijeka: INTECH Open Access Publisher, 2012: 53-76.

[8] LOHAN E S, BURIAN A, RENFORS M. Low-complexity unambiguous acquisition methods for BOC-modulated CDMA signals[J]. International Journal of Satellite Communications and Networking, 2008, 26(6): 503-522.

[9] FISHMAN P M, BETZ J W. Predicting performance of direct acquisition for the M-code signal[C]//Proceedings of the 2000 National Technical Meeting of the Institute of Navigation. Anaheim, CA: the Institute of Navigation, 2000: 574-582.

[10] MARTIN N, LEBLOND V, GUILLOTEL G, et al. BOC(x,y) signal acquisition techniques and performances[C]//ION GPS/GNSS 2003. Portland, OR: the Institute of Navigation, 2003: 188-198.

[11] LOHAN E S, BURIAN A, RENFORS M. Low-complexity unambiguous acquisition methods for BOC-modulated CDMA signals[J]. International Journal of Satellite Communications, 2008, 26(6): 503-522.

[12] BENEDETTO F, GIUNTA G, LOHAN E S, et al. A fast unambiguous acquisition algorithm for BOC-modulated signals[J]. IEEE Transactions on Vehicular Technology, 2013, 62(3): 1350-1355.

[13] JULIEN O, MACABIAU C, CANNON M E, et al. ASPeCT: Unambiguous sine-BOC(n,n) acquisition/tracking technique for navigation applications[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(1): 150-162.

[14] 朱银兵, 李豹, 刘睿. BOC信号改进码相位捕获算法研究[J]. 武汉大学学报(信息科学版), 2015, 40(3): 406-411.

ZHU Y B, LI B, LIU R. An improved code phase acquisition algorithm for BOC signal[J]. Geomatics and Information Science of Wuhan University, 2015, 40(3): 406-411 (in Chinese).

[15] YAO Z, LU M Q, FENG Z M. Unambiguous sine-phased binary offset carrier modulated signal acquisition technique[J]. IEEE Transactions on Wireless Communications, 2010, 9(2): 577-580.

[16] 柯颋, 胡修林, 刘禹圻, 等. 基于单元相关二次组合BOC无模捕获技术[J]. 华中科技大学学报(自然科学版), 2011, 39(6): 30-35.

KE T, HU X L, LIU Y Q, et al. Basic correlators quadric combination-based unambiguous acquisition technique of BOC signals[J]. Journal of Huazhong University of Science and Technology, 2011, 39(6): 30-35 (in Chinese).

[17] YAN T, WEI J L, TANG Z P, et al. Unambiguous acquisition/tracking technique for high-order sine-phased binary offset carrier modulated signal[J]. Wireless Personal Communications, 2015, 84(4): 2835-2857.

[18] QI J M, CHEN J P, LI Z B, et al. Unambiguous BOC modulated signals synchronization technique[J]. IEEE Communications Letters, 2012, 16(7): 986-989.

[19] LIU W, XI Y, DENG Z L, et al. Correlation combination ambiguity removing technology for acquisition of sine-phased BOC(kn,n) signals[J]. China Communications, 2015, 12(4): 86-96.

[20] HAYKIN S. Communication systems[M]. New York: John Wiley & Sons, 2001: 64-67.

UnambiguousacquisitiontechniqueforBOC(m,n)modulatedsignals

ZHANGHonglun1,2,BAXiaohui1,CHENJie1,*,ZHOUHang1

1.InstituteofMicroelectronicsofChineseAcademyofSciences,Beijing100029,China2.UniversityofChineseAcademyofSciences,Beijing100049,China

Multiplepeaksofautocorrelationfunctionofbinaryoffsetcarrier(BOC)modulatedsignalcanleadtoambiguityofsignalacquisition.Tosolvetheproblem,acorrelationmultiplicationside-peakcancellationtechnique(CMSCT)isproposed.Basedonthespecialpropertyofsub-correlationfunctionofBOCsignal,sidepeakscanberemovedbymultiplyingdifferentsub-correlationfunctions.Correspondingmodifiedalgorithmispresentedforthepurposeoftakingfulladvantageofall

datatoimprovetheacquisitionperformance.Thecomplexityoftheproposedalgorithmaswellasitsdetectionprobabilitybasedontheconstantfalsealarmratecriterionareanalyzedandcomparedwithotheralgorithms.TheresultofusingCMSCTforintermediatefrequencysamplingsignalofGalileoE1Cshowsthatthepresentedtechniquecaneffectivelysolvetheproblemofambiguousacquisition.

globalnavigationsatellitesystem;binaryoffsetcarriermodulation;unambiguousacquisition;correlationfunction;side-peakcancellation

2016-05-03；Revised2016-05-27；Accepted2016-06-14；Publishedonline2016-06-201341

URL：www.cnki.net/kcms/detail/11.1929.V.20160620.1341.006.html

NationalNaturalScienceFoundationofChina(61376027)

2016-05-03；退修日期2016-05-27；录用日期2016-06-14； < class="emphasis_bold">网络出版时间

时间：2016-06-201341

www.cnki.net/kcms/detail/11.1929.V.20160620.1341.006.html

国家自然科学基金(61376027)

＊

.E-mailjchen@ime.ac.cn

张洪伦， 巴晓辉， 陈杰， 等． 适用于BOC(m,n)信号的无模糊捕获技术J． 航空学报,2017,38(4):320394.ZHANGHL,BAXH,CHENJ,etal.UnambiguousacquisitiontechniqueforBOC(m,n)modulatedsignalsJ.ActaAeronauticaetAstronauticaSinica,2017,38(4):320394.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0194

V249.32

A

1000-6893(2017)04-320394-10

(责任编辑： 苏磊)

＊Correspondingauthor.E-mailjchen@ime.ac.cn