基于多维伪随机序列的压缩感知测量矩阵构造

芦存博，干红平，杨 悦，戎凯旋

(1.中国电子科技集团公司第54研究所 北京研发中心,河北 石家庄 050081; 2.重庆文理学院 电子电气工程学院,重庆 402160)

基于多维伪随机序列的压缩感知测量矩阵构造

芦存博1，干红平2，杨 悦1，戎凯旋1

(1.中国电子科技集团公司第54研究所 北京研发中心,河北 石家庄 050081; 2.重庆文理学院 电子电气工程学院,重庆 402160)

构造确定性测量矩阵对压缩感知理论的推广与应用具有重要的意义。源于代数编码理论，文中提出了一种基于多维伪随机序列的确定性测量矩阵构造算法。该算法选择迹表示函数产生二进制伪随机序列集合，并对其进行数值转换得到相应的双极性伪随机序列集合，此集合中的元素作为列向量进行排列即可组成文中的测量矩阵。理论分析和仿真实验表明，该方式构造的测量矩阵的重建性能优于同条件下的高斯随机测量矩阵。所构造矩阵可由线性反馈移位寄存器结构实现，易于硬件实现，具有实用价值。

压缩感知；测量矩阵；多维伪随机序列；迹函数

压缩感知(Compressed Sensing,CS)[1-2]由于考虑了信号的稀疏性或可压缩性而成为一种有效的信源处理技术。CS是对原始信号信息的采样，可实现以远低于奈奎斯特(Nyquist)的采样率去采样稀疏/可压缩信号。实际上是利用测量矩阵完成原始信号从高维空间到低维空间的线性投影，获取少量包含原始信号全部信息的投影值，然后在重建算法中利用了信号的稀疏性/可压缩性实现了原始信号的高概率精确重建。CS提出后引起了学术界的广泛关注，其在编码、信息论、物联网、高分辨率雷达、分布式存储系统、信道检测等应用科学领域和工程领域受到了高度关注。

测量矩阵可以分为两种类型：随机测量矩阵和确定性测量矩阵。对于前者，较常用的是高斯矩阵和伯努利矩阵。随机矩阵在理论上完美，在科研上被广泛应用，但是其随机性给硬件实现带来了不确定性，每一个随机数都要存储，这通常耗费大量的存储资源，给采样端带来了巨大压力，并且随机性对硬件的要求很高，不利于硬件实现，使得其实际应用受阻。而确定性测量矩阵的元素和值都是确定的，在信源端只用生成一次，可以克服这些不足。文中的有关工作就是基于确定性测量矩阵而展开的。现有的有不少技术可以用于构造确定性测量矩阵，如低密度奇偶校验(Low Density Parity Check,LDPC)码技术[3]、m序列技术[4]、混沌序列技术[5]、里所(Reed-Solomon,RS)码技术[6]。

本文将在文献[7]的基础上构造一种基于多维伪随机序列的确定性测量矩阵(Multidimensional Pseudo-random Sequences based Deterministic Measurement Matrix,MPSDMM)，并考虑相关性和重建性能的关系，分析所设计矩阵的相关性，从而优化所设计矩阵的重建性能。理论分析和仿真实验表明，该方式构造的测量矩阵MPSDMM的重建性能优于同条件下的高斯随机测量矩阵。

1 基础理论

1.1 CS数学模型

设x∈RN是k稀疏信号(k为信号非零值个数)，经过线性测量后得到观测信号y∈RM(M≪N),它们之间的关系可以表示为y=Φx，其中，矩阵Φ为测量矩阵，大小为M×N，此线性过程即为CS的数据采样过程。而信号的重建过程是非线性的，信号 可通过下述最小0范数优化问题精确重建

(1)

上述求解问题是NP-hard。CS理论证明了当测量矩阵Φ满足约束等距性(Restricted Isometry Property,RIP)[8]时，最小1范数优化问题的求解可以取代此问题的求解，即

(2)

该问题可以通过基追踪(Basis Pursuit,BP)算法[9]，得到与式(1)等价的最稀疏估计x。目前，也有一些直接求解式(1)的贪婪追踪类算法，例如，正交匹配追踪(Orthogonal Matching Pursuit,OMP)[10]算法。

1.2 RIP性质和相关性

定义1对于一个矩阵Φ∈RM×N(M≪N)，如果存在一个最小常数δK∈[0,1]对于任意的K稀疏信号x∈RN，都有下式成立

(3)

则称矩阵Φ满足K阶RIP，其中,δK称为约束等距常数(Restricted Isometry Constant,RIC)。

相关性(Coherence)是建立矩阵RIP的另一个重要方法，文献[11]指出矩阵的相关性跟RIP的关系：低相关性的矩阵满足RIP。矩阵的RIP[4,12-13]和相关性[3,5-6,14]均是描述矩阵性质的重要准则，本文将采用相关性对所构造测量矩阵的性质进行分析和说明。

定义2对矩阵A=(a1,a2,…,aN)∈RM×N，其相关性μ(A)定义如下

(4)

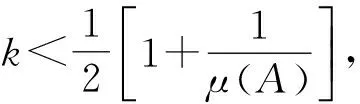
1.3 迹函数

假设β为有限域GF(q)的本原域元素，则GF(q)所有域元素可由0和β的幂次生成，即：0，β0=1，β,…,βq-2。其中后q-1个非零元素构成乘法群GF(q)(〗0}，也可记作GF(q)*。为方便描述起见，也可将GF(q)所有元素表示为{0,1,…,q-1}。

定义2设n,m是正整数，且m整除n，则从GF(2n)到GF(2m)的迹函数为

(5)

2 测量矩阵构造

矩阵MPSDMM是由+1和-1组成的双极性矩阵，大小为(2n-1)×22n(n≥5)，其具体实现步骤如下：

步骤1选取迹表示函数式：根据信息长度N=22n，计算出n，判断n为奇数还是偶数，当n为奇数时，选择式(6)；当n为偶数时，选择式(7)

(6)

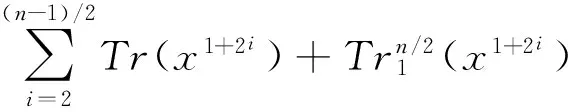
(7)

这里，x∈GF(2n)*，λ0,λ1∈GF(2n)

(8)

步骤3将上述得到的22n个双极性序列c0,0，c0,1，c0,2,…,c0,2n-1,c1,0,c1,1,c1,2,…,c1,2n-1,c2,0,…,c2n-1,2n-1作为列向量进行排列即可组成本文的测量矩阵。

从上述构造过程可以看出：一旦给定有限域上的迹表示函数式(6)或式(7)，则能确定出所构造矩阵MPSDMM的每一个元素值；MPSDMM矩阵的{-1,1}元素结构非常便于硬件实现，数值转换函数式(8)的本质是元素替换，在硬件实现上只用改变相应元素的输出即可，非常简单。矩阵MPSDMM的生成过程中，使用的是文献[7]的迹表示函数，从文献[7]可得，MPSDMM矩阵可由LFSR结构实现，易于硬件实现，具有实用价值。

3 理论性能分析

本节首先给出所构造MPSDMM矩阵A的相关性大小μ(A)，如下述定理1所示。

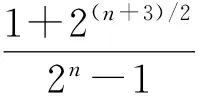
证明由于矩阵A的列向量是由双极性序列集合{c0,0，c0,1，c0,2,…,c0,2n-1,c1,0,c1,1,c1,2,…,c1,2n-1,c2,0,…,c2n-1,2n-1}构成，所以

(9)

由于序列ci,j和ck,l均在{-1,1}上取值，则有

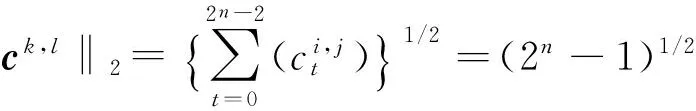
(10)

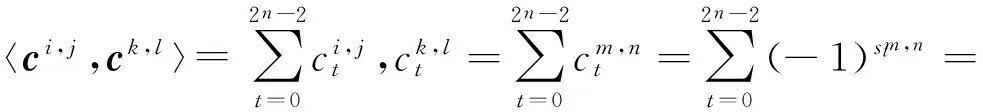
(11)

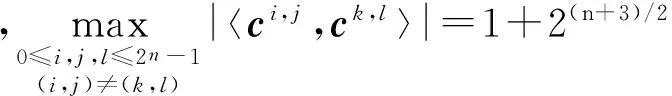
减小相关性可使重建性能提高，为了比较本文中的MPSDMM矩阵A和同条件下的高斯随机测量矩阵B的重建性能，可以比较这两个矩阵相关性的大小。

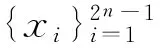
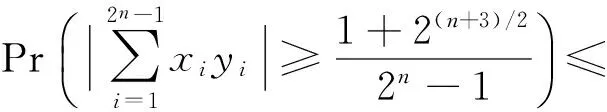
(12)

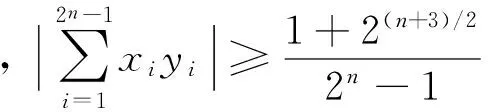
4 实验仿真及分析

比较了本文矩阵MPSDMM和相同大小的高斯随机测量矩阵Gaussian在无噪声条件和有噪声条件下的重建性能，其中矩阵MPSDMM分为以下两种情况：(1)n=8对应于n是偶数的情况，此时矩阵大小为255×65 536；(2)n=7对应于n是奇数的情况，此时矩阵大小为127×16 384。

在一个长度为22n的信号中，随机的选取k个位置，其取值服从标准的高斯分布，其它位置的取值为0，这样就得到了一个k稀疏信号x。对每个稀疏度k，用Matlab生成1 000次，重构算法选取OMP算法，若重建结果xR满足‖x-xR‖2≤10-6，则重建实验成功，重建概率即为精确重建次数与总次数的比值。Gaussian矩阵的每一个元素取值服从独立同分布的标准正态分布。

4.1 无噪声重建

实验1对大小为255×65 536的测量矩阵MPSDMM，稀疏度k=18～72，不同稀疏度下的重建概率对比曲线如图1(a)所示；对大小为127×16 384的测量矩阵MPSDMM，稀疏度k=7～49，不同稀疏度下的重建概率对比曲线如图2(a)所示。

如图1(a)和图2(a)所示，矩阵MPSDMM的信号恢复效果比相同大小的Gaussian矩阵效果好，这是由于前者的相关性小于后者，更有利于信号重构。

图1 MPSDMM大小为255×65 536的情况

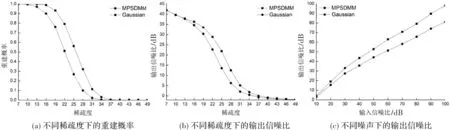
图2 MPSDMM大小为127×16 384的情况

4.2 有噪声重建

实验2选取信噪比为30 dB的被采样信号，对大小为255×35 536的测量矩阵MPSDMM，稀疏度k=18～72，不同稀疏度下的输出信噪比对比曲线如图1(b)所示；对大小为127×16 384的测量矩阵MPSDMM，稀疏度k=7～49，不同稀疏度下的输出信噪比对比曲线如图2(b)所示。

如图1(b)和图2(b)所示，矩阵MPSDMM的信号恢复效果比相同大小的Gaussian矩阵效果好，这是因为矩阵的相关性越小，越有利于信号重构。

实验3在不同噪声条件下,对大小为255×35 536的测量矩阵，选取稀疏度为42的被采样信号，所得重建曲线对比如图1(c)所示；对大小为127×16 384的测量矩阵，选取稀疏度为20的被采样信号，不同稀疏度下的重建概率对比曲线如图2(c)所示。

从图1(c)和图2(c)可知，在不同输入噪声条件下，采用本文所构造的MPSDMM矩阵，进行重建后的输出信噪比较采用高斯随机测量矩阵的要高。

通过上述仿真发现，MPSDMM矩阵比相同条件下的高斯随机矩阵抗噪声性能要好，说明文中矩阵在无噪声环境和噪声环境中都具有良好的重建性能，即表明文中所提矩阵的高效性和实用性。

5 结束语

本文在多维伪随机序列的基础上构造了一种双极确定性高效测量矩阵-MPSDMM，并通过理论推导，得到所构造矩阵的相关性大小。理论分析和仿真实验表明，在相同大小的条件下，MPSDMM矩阵在无噪声环境和噪声环境下的重建性能都优于相应的高斯随机矩阵。矩阵MPSDMM具有高效性和实用性，可由LFSR结构实现，易于硬件实现，有利于CS理论的实用化。本文计划下一步在FPGA中完成MPSDMM测量矩阵的生成，搭建实验平台，对MPSDMM测量矩阵在实际应用中的性能作进一步深入研究。

[1] Candès E J,Romberg J,Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transations on Information Theory,2006,52(2): 489-509.

[2] Donoho D L. Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4): 1289-1306.

[3] Zhang J,Han G,Fang Y. Deterministic construction of compressed sensing matrices from protograph LDPC codes[J]. IEEE Signal Processing Letters,2015,22(11):1960-1964.

[4] 权磊,肖嵩,薛晓,等.低复杂度压缩感知中的快速观测方法[J].西安电子科技大学学报,2017,44(1): 114-119.

[5] Zeng L,Zhang X,Chen L,et al. Deterministic construction of toeplitzed structurally chaotic matrix for compressed sensing[J]. Circuits,Systems,and Signal Processing,2015,34(3): 797-813.

[6] Mohades M M,Mohades A,Tadaion A. A reed-solomon code based measurement matrix with small coherence[J]. IEEE Signal Processing Letters,2014,21(7): 839-843.

[7] Yu N Y,Gong G. A new binary sequence family with low correlation and large size[J]. IEEE Transactions on Information Theory,2006,52(4):1624-1636.

[8] Candès E J,Tao T. Decoding by linear programming[J]. IEEE Transactions on Information Theory,2005,51(12): 4203-4215.

[9] Chen S S,Donoho D L,Saunders M A. Atomic decomposition by basis pursuit[J]. SIAM Journal on Scientific Computing,1998,20(1):33-61.

[10] Tropp J. Greed is good: algorithmic results for sparse approximation[J]. IEEE Transactions on Information Theory,2004,50(10): 2231-2242.

[11] Bourgain J,Dilworth S,Ford K,et al. Explicit constructions of RIP matrices and related problems[J]. Duke Mathematical Journal,2011,159(1): 145-185.

[12] Gan H,Li Z,Li J,et al. Compressive sensing using chaotic sequence based on chebyshev map[J]. Nonlinear Dynamics,2014,78(4): 2429-2438.

[13] Castorena J,Creusere C D. The restricted isometry property for banded random matrices[J]. IEEE Transactions on Signal Processing,2014,62(19): 5073-5084.

[14] Li S,Ge G. Deterministic sensing matrices arising from near orthogonal systems[J]. IEEE Transactions on Information Theory,2014,60(4): 2291-2302.

[15] Donoho D L,Elad M. Optimally sparse representation in general (nonorthogonal) dictionaries via minimization[J]. Proceedings of the National Academy of Sciences,2003,100(5): 2197-2202.

[16] Haupt J,Bajwa W U,Raz G,et al. Toeplitz compressed sensing matrices with applications to sparse channel estimation[J]. IEEE Transactions on Information Theory,2010,56(11): 5862-5875.

Construction of Compressed Sensing Measurement Matrix Based on Multidimensional Pseudo-random Sequences

LU Cunbo1，GAN Hongping2，YANG Yue1，RONG Kaixuan1

(1. Beijing R&D Center,The 54th Research Institute of China Electronics Technology Group Corporation,Shijiazhuang 050081,China;2. School of Electrical and Electronic Engineering,Chongqing University of Arts and Sciences,Chongqing 402160,China)

It is significant to construct deterministic measurement matrix for the promotion and application of the compressed sensing theory. Originating from the algebraic coding theory,this paper presented a construction algorithm of multidimensional pseudo-random sequences based deterministic measurement matrix. This algorithm first chose trace representative function to generate the set of binary pseudo-random sequence. And then,the generated set of binary pseudo-random sequence was output as the corresponding set of bipolar pseudo-random sequence by numeric convert. The elements of bipolar sequence set arranged itself to constitute the measurement matrix as column vectors. Theoretical analysis and simulation results show that the proposed matrix can obtain better reconstruction results than the corresponding Gaussian random measurement matrix. The proposed matrix can make the hardware realization convenient and easy by means of Linear Feedback Shift Register (LFSR) structures,thus having its practical value.

compressed sensing; measurement matrix; multidimensional pseudo-random sequences; trace function

TN919.81；TP391.41

A

1007-7820(2017)11-068-05

2016- 12- 20

中国电子科技集团公司第五十四研究所发展基金；国家自然科学基金(61372069)；高等学校学科创新引智计划(111计划)(B08038)；永川区科委自科基金(YCSTC,2015NC2001)；重庆市教委科学技术研究项目(KJ1501105)

芦存博(1989-)，男，博士，工程师。研究方向：网络编码等。干红平(1989-),男,硕士,讲师。研究方向：压缩感知测量矩阵设计及加密算法。杨悦(1981-),女,博士,高级工程师。研究方向：网络数据分析。戎凯旋(1986-),男,博士,工程师。研究方向：遥感图像,压缩感知。

10.16180/j.cnki.issn1007-7820.2017.11.019