基于C#牛顿潮流算法的分析
王医强,张莉萍 ,陈宇晨,范 蕊
(上海工程技术大学 电子电气学院,上海 201620)
基于C#牛顿潮流算法的分析
王医强,张莉萍 ,陈宇晨,范 蕊
(上海工程技术大学 电子电气学院,上海 201620)
针对Matlab与C#混合开发潮流计算程序时平台间存在通信不便的问题,需要通过分析牛顿拉夫逊潮流算法在C#上的运行效率和可靠性,验证使用C#是否能更好的开发潮流计算程序,从而统一开发平台。选择在Visual Studio2013平台上,使用C#语言实现牛顿拉夫逊法潮流计算,并且对C#潮流计算的结果和运行时间与Matlab潮流计算的结果和运行时间进行对比分析。求解IEEE4系统的电网数据得出C#语言运算时间比Matlab要少55 ms,所求节点数据与Matlab所求出的数据相比,相差精度在10-5数量级。通过实验得出基于C#牛顿潮流算法可靠性高,运行效率高,可用于开发潮流计算程序。
导纳矩阵;雅可比矩阵;关联矩阵;牛顿法
潮流计算中常用的算法是牛顿拉夫逊法,分析该算法时大多是在Matlab软件上。随着当前智能电网的不断发展,开发软件功能的不断完善,数据库技术的突破,对潮流计算的要求也有所变化,以前的Matlab平台无法满足在线潮流计算,计算速度也无法与编译型语言相比。
文献[1]中利用Matlab完成潮流计算算法,VB完成程序的界面,通过ActiveX技术实现了Matlab与VB间的数据通信[1]。由于Matlab和C#均是基于C语言的高级语言的特点,文献[2]中利用该特点实现C#和Matlab的混合编程[2],C#语言用于实现界面的开发,Matlab用于完成庞大的数值运算和图像生成。文献[3]中分析了Basic、Fortran和Matlab等高级语言在潮流计算中的各自特点[3],针对潮流计算数学模型,在Matlab上开发出了潮流算法。文献[4]中介绍了一种基于GIS[4]的潮流算法,并在C#语言的基础上开发与该算法相关的应用程序。文献[5]中从潮流计算的意义、目的、方法以及实验等方面对潮流计算进行了分析[5]。文献[6]中运用MatPower软件进行潮流计算,并且把MatPower潮流计算的最终结果与Matlab和SimuLink[6]潮流计算的结果做比较。文献[7]中针对牛顿类潮流计算的初值敏感性问题提出牛顿潮流计算的收敛性定理,给出牛顿类潮流收敛的充分条件,解决了用牛顿法进行潮流计算时因初值选取不当使潮流收敛过慢甚至无法收敛的问题[7]。文献[8]中在传统Fast-ICA算法的基础上,为了加快算法的收敛速度,提高算法的运行效率利用8阶收敛的牛顿迭代方法对Fast-ICA算法进行优化[8]。文献[9]中利用Matlab研究改进牛顿算法在配电网潮流计算中的应用[9]。文献[10]中对直角坐标和极坐标牛顿法潮流计算的速度进行比较,在PV节点数较少的情况下直角坐标牛顿法的潮流计算速度快于极坐标牛顿法[10],在PV节点数较多的情况下则相反。文献[11]中在一阶牛顿法的基础上利用一阶牛顿法的修正量作为预测量,用传统牛顿法进行迭代计算,使用Matlab编程仿真,实验结果表明该方法迭代次数少,收敛性好[11]。
1 牛顿法原理
图1 单变量函数牛顿迭代法[12]。
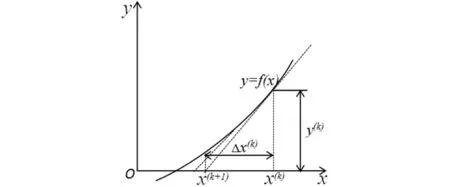
图1 单变量函数牛顿迭代法
为了更好地引用牛顿法的数学原理,首先对单变量方程和相关公式分析。设上图中单变量方程为
f(x)=0
(1)
当图中k=0时设x(0)为解的近似值,与真解的误差为Δx(0),则
f(x(0)+Δx(0))=0
(2)
将上式左边的函数在x(0)附近展开为泰勒级数,由于Δx(0)很小,则Δx(0)的二次及以上的阶次可略去,从而得到以下修正方程
f(x(0)+Δx(0))=f(x(0))+f′(x(0))Δx(0)=0
(3)
解该方程可得到修正量为
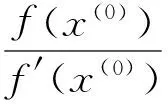
(4)
根据以上修正量可得迭代一次后近似解为
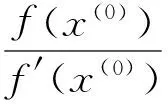
(5)
接下来将单变量的牛顿拉夫逊法应用到求解多变量非线性代数方程。设多变量非线性代数方程为
(6)
将各变量的初值和各变量的修正量代入以上方程组得
(7)
将上式中的n个多元函数在初始值附近分别展成泰勒级数,并略去含有修正量的二次及以上阶次的各项,可得到以下方程组
(8)
根据方程组可转化为矩阵形式
(9)
多变量非线性方程的迭代过程如单变量非线性方程一样,因此可将第k次迭代的修正方程写成如下矩阵形式,便于应用到潮流计算中
F(X(k))=-J(k)ΔX(k)
X(k+1)=X(k)+ΔX(k)
(10)
以上J为雅可比矩阵,X为多变量列向量。
通过从单变量到多变量牛顿法数学原理的分析,能够更好的应用牛顿法。
2 潮流计算数学模型
基于以上牛顿法的数学原理分析,将牛顿法应用到潮流计算,将电网中的节点数据和支路数据引入牛顿法中得到牛顿法潮流计算数学模型。由于在电网节点数比较少的情况下,直角坐标表示的节点电压方程比极坐标表示的节点电压方程收敛速度快,此次分析的节点电压数比较少,因此潮流计算中的节点电压用直角坐标表示。
节点电压可表示为
Ui=ei+jfi
(11)
导纳矩阵为
Yij=Gij+jBij
(12)
根据电力系统实际运行条件,电网节点一般分为PQ节点、PU节点、平衡节点,平衡节点电压相位一般为零,幅值给定,因此不参与到牛顿法迭代计算中。约束条件包括电压约束、有功功率和无功功率约束以及相位差约束。潮流计算的数学模型是根据以下式(13)和式(14)、式(15)求得的步长进行逐步线性化,从而求得满足电网运行要求的近似解
(13)
通过式(13)和导纳矩阵的实部以及虚部数据可求得PQ节点的有功功率和无功功率。将式(13)代入式(14)中可求得有功功率和无功功率的迭代步长
(14)
对于PU节点时,可通过式(15)求得有功功率迭代步长和电压迭代步长
(15)
将以上各个变量的步长放入到矩阵中,逐步线性化的过程可以用修正方程(16)表示,其中J为雅可比矩阵,ΔW里的变量为节点功率的步长,ΔU是每次迭代时电压的变化量
ΔW=-JΔU
(16)
雅可比矩阵中的元素为各个功率步长对节点电压的偏导数,对偏导数化简后得到雅可比矩阵元素关于导纳矩阵元素间的关系,通过对雅可比矩阵中的不同节点分布规律求出该矩阵中的各个元素。
通过高斯求逆法可对修正方程进行求解,求解后可得到节点电压的步长,从而进一步求得下一次计算的初始电压数据。
3 实验及分析
使用Visual Studio2013和Matlab2014a作为程序开发平台,在主频为3.30 GHz,运行内存为4 GB的计算机上对IEEE4系统进行潮流计算。在Visual Studio2013上建立C#语言的工程后,根据图2开发潮流计算程序。牛顿法潮流计算需要先求出导纳矩阵Y。求解导纳矩阵时,采用关联矩阵法[13]。根据网络拓扑图对支路编号和方向标识,对于n个节点m条支路的有向图,可以得到一个n行m列的关联矩阵A。通过网络已给的支路参数可得支路阻抗矩阵Z,根据以下公式可求出导纳矩阵
Y=AZ-1AT
(17)
编程时对关联矩阵的处理需要使用非线性映射法对矩阵中的数据进行编号,根据编号可访问到矩阵中的元素。
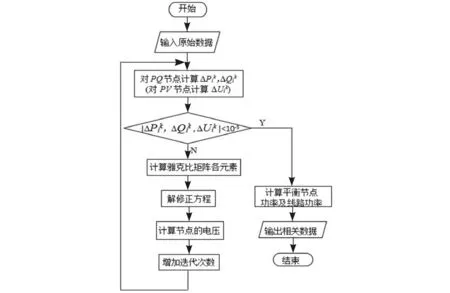
图2 牛顿法潮流计算流程图
导纳矩阵求出后,需要对原始数据的存放进行处理,根据节点编号的顺序将节点数据分开存放到各个对应数组。迭代计算中编程重点在于求雅可比矩阵,雅可比矩阵中存放的是对各个电压自变量的偏导数,偏导数的计算公式也各自不一。如何根据不同情况计算偏导数,并且存放到雅可比矩阵对应的位置上需要使用一些相关的技术进行处理。其次如何选择适当的方法求解修正方程也很重要,常用的方法包括高斯消去法和三角分解法以及稀疏矩阵求解技巧。由于算例中的节点数比较少,程序中使用三角分解法求解修正方程。对于矩阵类[14]开发的要求也就增加了,需要在该类中设计出能够进行三角分解的方法,程序中使用的是高斯法对雅可比矩阵求逆。其中复数类的设计是便于节点中的复数数据的存放,以及潮流计算后能够使输出的数据更加直观,便于与Matlab计算出来的数据比较。
根据IEEE4节点系统对应的标幺制初始节点电压和功率数据在Visual Studio2013上使用C#语言开发的牛顿法潮流计算程序求得每次迭代节点不平衡量数据如表1所示。
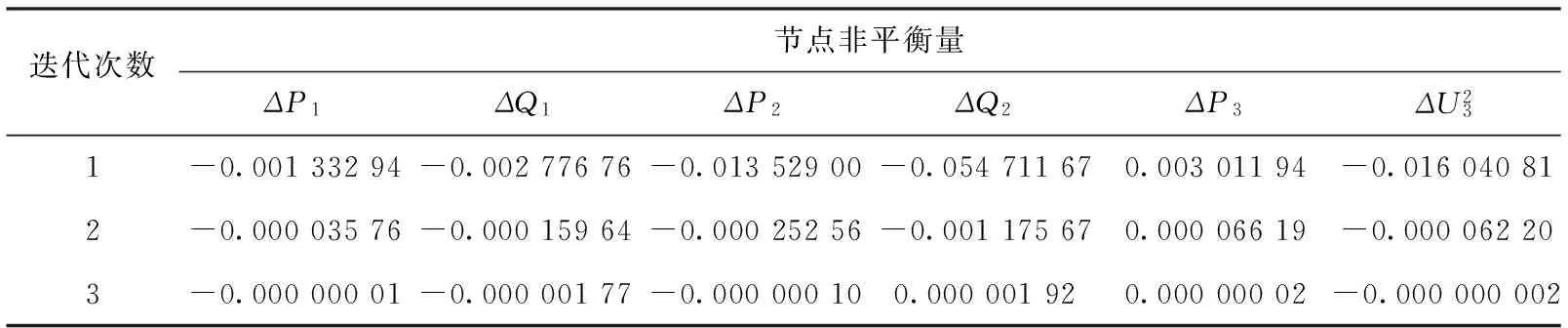
表1 C#节点非平衡量
通过上面求出的节点非平衡量和修正方程,使用高斯求逆法可得到节点电压修正量,与对应的节点数据。根据以上方法可求得节点电压如下表2所示。
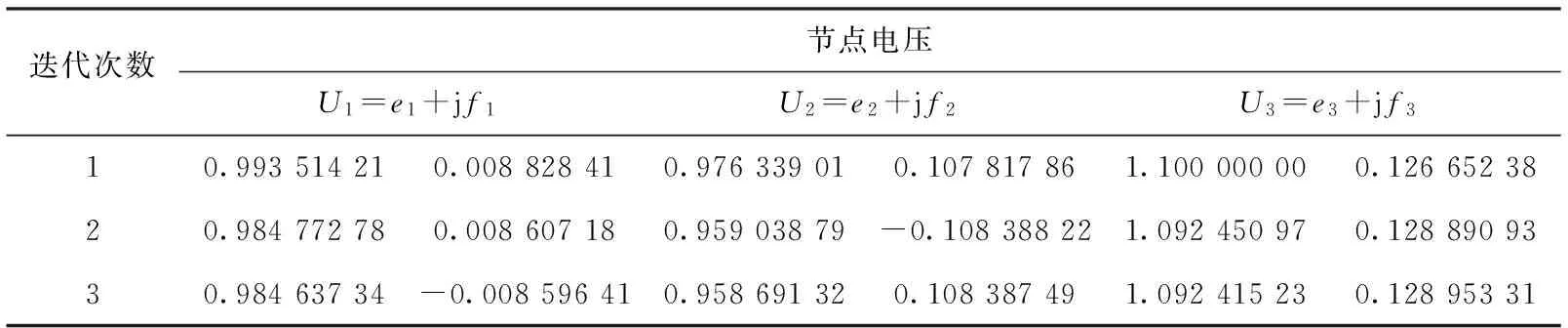
表2 C#的节点电压数据
根据C#牛顿潮流算法同一原理,使用Matlab2014a平台对同一节点系统进行运算得到以下表3的节点非平衡量和表4的每次迭代过程中的节点电压数据。
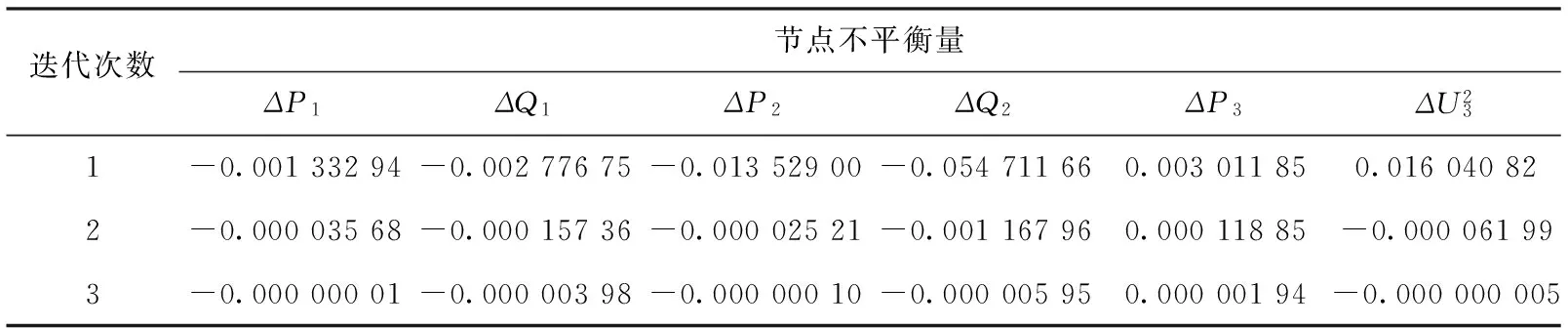
表3 Matlab节点非平衡量

表4 Matlab节点电压
对以上两个不同平台上计算出的数据进行比较分析,C#上求解出的各个变量与Matlab上求出的各个变量相比,其相差<0.000 01。由此可得出C#用于开发潮流计算程序是比较合理的,而且使用C#的优势在于能够更好的实现人机交互界面,不需要在Matlab与C#之间进行跨平台操作。
4 结束语
文中得出在两种平台上算出的数据误差很小,但运行时间相差较大。如表5所示。

表5 C#与Matlab运行时间比较
对表6中运行时间进行比较,C#的计算速度明显比Matlab快,表明C#语言用于实现潮流计算算法是可行的,并且由于ASP.NET技术也是以C#为核心,这对以后开发实时潮流计算软件提供了可靠的依据。
目前小型电力系统的潮流计算程序都是使用C或者C++以及Matlab等开发,MatPower也只提供牛顿拉夫逊法、高斯赛德尔法、快速解耦算法(XB版)、快速解耦算法(BX版)等4种潮流计算方法[15],而且MatPower常被用来研究电力系统负荷[16]用于实现在线潮流计算比较困难。同时文中算法对于节点数较多的电力系统进行潮流计算时,初值选取困难,无法收敛[17]。因此,在以后的研究中需要对牛顿法数学模型进行改进;另外由于C#访问数据库的便利性和潮流计算的高效性等特点,在后续研究中可以充分利用C#的这些特点实现从算法到交互界面以及调取数据库信息平台的统一,从而快速的进行潮流计算。
[1] 张菁,陈宇晨.Matlab与VB的集成在电力系统潮流计算中的应用[J]. 微计算机信息,2007,23(20):60-62.
[2] 李佳泽,陈聪,张鹏. C#与Matlab混合编程在简单潮流计算可视化窗体设计中的应用[J]. 数字技术与应用,2016,33(4):159-159.
[3] 张宁,江红梅,张渭. 基于Matlab的电力系统潮流计算[J]. 西北农林科技大学学报:自然科学版,2004,32(12):124-126.
[4] 张立国,赵睿明,霍利民,等. 基于GIS的配电网实时潮流计算软件的开发[J].微计算机信息,2006,22(5):287-289.
[5] 杜伟伟.石河子电网的潮流计算及分析[J].石河子科技,2016,40(3):53-55.
[6] 郭桂静,徐道安,师秀凤. 基于MatPower的电力系统潮流计算[J].企业导报,2016,16(12):172-174.
[7] 孙秋野,陈会敏,杨家农,等.牛顿类潮流计算方法的收敛性分析[J].中国电机工程学报,2014,34(13):2196-2200.
[8] 陈梦,何选森.基于八阶收敛牛顿迭代的Fast-ICA改进算法[J].计算机工程与应用,2016,52(5):2-6.
[9] 刘云舒,吴玮华,余志远,等.基于改进牛顿算法的配电网潮流计算[J].通信电源技术,2015,32(6):162-164.
[10] 邵尉哲,王宇俊,万新儒,等.直角坐标与极坐标牛顿法潮流计算速度的比较[J].南昌大学学报:工科版,2016,38(1):98-102.
[11] 段俊东,薛静杰,栗维冰.基于牛拉法的预估校正潮流计算算法[J].河南理工大学学报:自然科学版,2015,34(3):396-399.
[12] 何仰赞,温增银. 电力系统分析[M].4版.武汉:华中科技大学出版社,2016.
[13] 陈明,李银红,石东源,等.节点导纳矩阵和阻抗矩阵的互感支路组整体追加方法[J].电工技术学报,2016,31(21):94-101.
[14] 周长发.C#数值计算算法编程[M].北京:电子工业出版社,2007.
[15] 陈辰,李森,李领娟.基于MatPower的负荷中断分析[J].电子科技,2016,29(6):11-14.
[16] 孟祥,沈澍东.基于Matlab和MatPower的孤岛判别与处理[J].电子科技,2015,28(10):123-125.
[17] Milano F.Continuous Newton’s method for power flow analysis[J].IEEE Transactions on Power Systems,2009,24(1):50-57.
Analysis of Newton Power Flow Algorithm Based on C#
WANG Yiqiang,ZHANG Liping,CHEN Yuchen,FAN Rui
(School of Electronic and Electrical Engineering,Shanghai University of Engineering and Science,Shanghai 201620,China)
The Matlab and C# mixed development flow calculation program of communication problems between the platform and the inconvenience,it needs to run the efficiency and reliability of Newton Ralph Xun power flow algorithm in the analysis of the C#,and verify whether the use of C# can better develop the flow calculation program,then unify development platform. The result of C# language computing time is less than 55 ms Matlab when solve the grid data of IEEE4 system,the difference in accuracy of the node data by C# compared to the data obtained by Matlab in the 10-5orders of magnitude. The experimental results show that the C# Newton power flow algorithm has high reliability and high efficiency. It can be used to develop the power flow calculation program.
admittance matrix;jacobian matrix;incidence matrix;newton method
O151.21;TM74
A
1007-7820(2017)11-063-05
2017- 01- 05
国家自然科学基金(61673257)
王医强 1991,男,硕士研究生。研究方向:配电网网损分析等。张莉萍 1962,女,硕士,硕士生导师。研究方向:智能控制等。陈宇晨(1958-),男,博士,硕士生导师。研究方向:电力系统分析等。
10.16180/j.cnki.issn1007-7820.2017.11.018

