二乘二取二系统的一种新降级策略研究

张永贤，邹力棒，吴文杰，廖肇聪

（华东交通大学电气与自动化工程学院，江西 南昌 330013）

二乘二取二系统的一种新降级策略研究

张永贤，邹力棒，吴文杰，廖肇聪

（华东交通大学电气与自动化工程学院，江西 南昌 330013）

随着国内轨道交通行业的高速发展，系统的安全性和可靠性越来越受到重视。以提高轨道交通控制中常用的二乘二取二安全计算机的可靠性和安全性为目标，分析了几种常用冗余结构的可靠性，进一步提出了一种基于三取二冗余结构及二乘二取二冗余结构的新降级工作策略。在考虑多模故障的情况下，分析了该系统所有工作状态以及各状态之间的转移关系，依此建立马尔可夫状态转移模型，通过MATLAB分析新降级工作策略下系统的安全性和可靠性。与传统二乘二取二系统进行对比，新降级工作策略下系统具有更高的可靠性。

二乘二取二；可靠性；安全性；多模故障；马尔可夫模型

随着高速铁路及城市轨道交通的快速发展，安全控制问题受到越来越多的关注。安全计算机是轨道交通列车车载与地面控制系统的核心，直接影响到列车能否安全可靠并且高效地运行[1]。采用冗余容错结构可提高安全计算机的可靠性和安全性，常用的冗余容错结构有二乘二取二、带自诊断的双机热备、三取二表决等[1-5]。文献[6]中列出了所有表决冗余系统可靠性的基础计算方法，这种计算方法有一定的局限性，只适用于初步的冗余结构研究，现有文献中大多使用马尔科夫模型结合系统工作情况进行分类[7-9]。现有二乘二取二可靠性和安全性分析相关文献没有考虑由共因失效[9]导致的多模故障率（包括双模失效和三模失效），而多模故障在在安全性和可靠性分析中不可忽略。几种常见安全结构体系中，三取二表决系统可靠性比二乘二取二系统可靠性要高。为了提高二乘二取二系统的可靠性，提出了一种基于总线表决的新的二乘二取二结构的降级工作策略，在考虑多模故障的情况下，利用马尔可夫理论将系统工作状态进行划分，详细研究该模式下的状态转移，分析新工作策略下系统的可靠性和安全性。

1 二乘二取二冗余系统工作策略

1.1 传统降级策略

如图1所示，二乘二取二结构包含两个比较子系统，分别为A系和B系，系内包括两个具有故障检测功能的运算模块和二取二表决器。处于主系状态的二取二表决器对两个模块的输出进行比较，相同则该系的输出作为系统的输出，不同则进行主备切换，由于备系和主系一直保持任务同步，备系接替主系任务并转为主系。如切换成功则原主系进入维修状态，不成功则进入停机状态，系统输出导向安全侧。

1.2 新降级策略

如图2所示，4个模块的输出通过4条具有安全协议的总线（BUS1，BUS2，BUS3，BUS4）传入总线控制器，与传统二乘二取二结构相比，不再需要主备切换和二取二表决器，但增加了1个多功能的总线控制器。总线控制器可进行一定故障诊断、主备系数据同步、状态信息记录等功能，但其主要功能是根据四路总线上的信息进行表决。

所设计的二乘二取二新降级工作策略是当A系或B系之中任意一个模块产生可检测故障时，由二乘二取二结构降级为三取二表决结构，当再次出现可测故障时，进入二取二表决结构。而传统工作策略中当单一模块出现故障后直接降级为二取二结构，故障模块系中另一模块没有发挥出应有的作用，而二乘二取二新降级工作策略能使得系统充分发挥故障系非故障模块的作用，使系统具有更高的可靠性。

图1 二乘二取二系统结构图Fig.1 Architecture of double 2-out-of-2

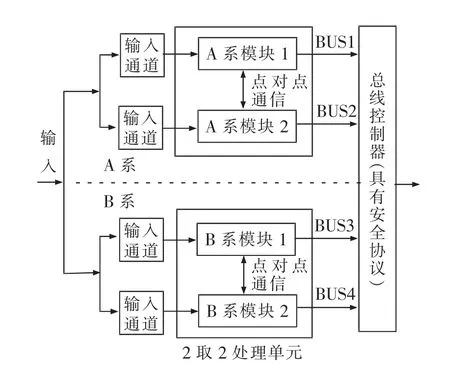
图2 基于总线表决的二乘二取二结构图Fig.2 Architecture of double 2-out-of-2 based on bus voting

当检测出单一故障模块时，故障系无故障模块通过该路总线发送屏蔽同系故障模块码及当前计算结果，总线控制器根据接收到屏蔽码来改变表决策略，发送模式码给各模块，各模块可在完成基本任务的同时还可进行故障诊断和故障恢复任务，而总线控制器进行数据备份且进行表决输出，总线控制器工作流程见图3。图中A1、A2、B1、B2分别是A系、B系的两模块输出。关于该总线控制器，需要说明的是：① 总线控制器的表决输出使用动态驱动和安全输出接口，保证总线控制器在发生输出故障时也不会导向危险侧；② 总线控制器的表决功能具有安全协议的，且表决的信息需通过总线与A系和B系模块进行核对，总线控制器的表决输出可认为是二乘二取二冗余系统的表决输出，总线控制器负责组合A、B系模块1与模块2的输出结果并进行表决。因此，在后文建立马尔科夫模型时，不考虑总线控制器故障，其表决可靠度与传统二乘二取二冗余系统中的二取二表决器一致。

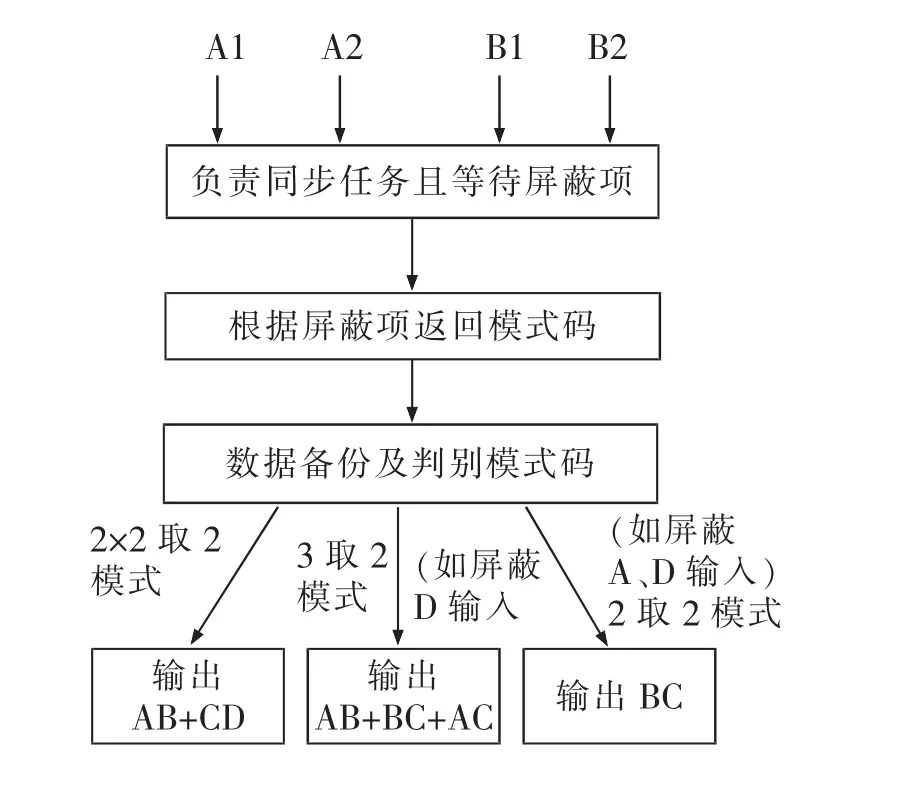
图3 总线控制器工作流程图Fig.3 Bus controller diagnosis and voting flow

2 系统的可靠性和安全性分析

可靠性R（t）是指系统在一定的环境下，在给定的时间内完成预定功能的概率,可靠的系统只能在一定程度上保证是个相对安全的系统，安全性S（t）是系统避免不可接受的伤害风险的概率，本文中是指不考虑其他外部因素下系统不产生危险输出的概率。设单个模块的可靠度为R（t），不可靠度为1-R（t），则n个模块冗余结构的可靠度RS（t，n）为[9]

其中n中取k表决冗余结构的可靠度RS（t，k/n）为[2]

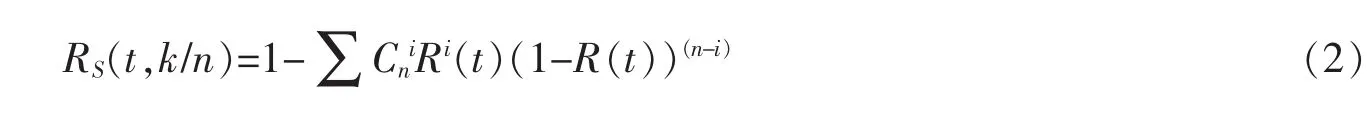
式中i取值为1～k-1，表示该冗余结构中i个模块正常工作，n-i个模块失效。假设单个模块的在t时刻的可靠度R=0.9，根据式（1）和式（2），分别得出该时刻的三取二、二乘二取二、四取三冗余结构的可靠度

结果表明，三取二表决系统比二乘二取二冗余表决系统在可靠性上具有一定优势，而四取三表决可靠性反而比三取二可靠性低。二乘二取二系统要在可靠性上获得进展必须在其工作策略上进行优化。在更为详细地分析二乘二取二冗余系统时，作以下假设：

1）4个模块的设计完全相同，即单模故障率、修复率和故障检测覆盖率均相同且是常数，共因失效导致的双模故障率等于三模故障率且是常数。

2）具有安全通信协议总线的表决可靠度与传统二乘二取二系统中的硬件二取二比较器相同，同设为1。

3）在某一时刻只能同时发生一种类型的故障，即单模故障、双模故障或三模故障。

系统模块失效不仅分为单模失效、双模失效、三模失效，还可进一步分为可测失效和不可测失效。设单模失效率为λ，双模失效率和三模失效率都为β。故障覆盖率为c，1-c为故障未检测到的概率，单模块维修率为μ，假设系统各模块在t时刻正常工作，故障失效服从指数分布，则在t+Δt时刻发生可测单模故障的概率是p=1-e-cλΔt，当Δt很小时，可简化为cλΔt。依此可推出双模或三模可测故障概率为cβΔt，其不可测双模或三模故障概率（1-c）βΔt。

基于以上假设，二乘二取二冗余系统传统工作策略状态如表1。本文设计的新降级工作策略见表2，与传统工作策略相比，增加2种状态，一种是可修复三取二状态，一种是不可修复三取二状态。

表1 传统工作策略状态表Tab.1 State of traditionalworking strategy

表2 新降级工作策略状态表Tab.2 State of new degradation working strategy

2.1 传统降级策略下的状态转换马尔可夫模型

用来分析系统可靠性和安全性常用的方法有动态故障树分析法[11]、马尔可夫模型分析法。动态故障树法必须区分任何一种失效模式，特别适用于具有动态随机相关性故障的容错、冗余系统以及顺序相关性系统的可靠性建模和分析。但是它对于研究新的工作模式并不合适，过程复杂。马尔可夫模型分析法是一种常用的分析可靠性和安全性的方法，且模型简易明了，能够很好的描述系统在正常运行、故障、维修、虚警等状态之间的转移过程[12]。缺点是模型状态空间的增加随冗余系统规模大大增加，使得难以计算。

本文对新系统进行了合理的模式分类，其系统模型较小，求解简单。根据传统工作策略，结合表1，其传统二乘二取二系统状态转换图见图4。

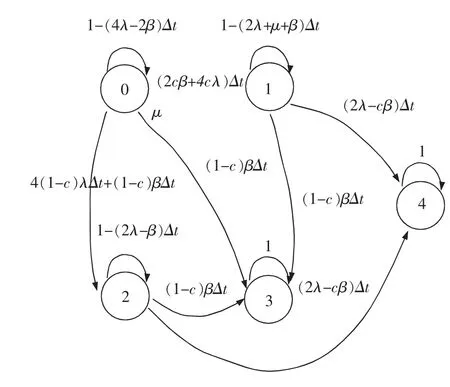
图4 传统二乘二取二系统状态转换图Fig.4 Markov state transition of traditional double 2-out-of-2 system

状态0到状态1含义为正常二乘二取二状态下发生单个模块的可测故障和发生双模可测失效转换到二取二状态，根据其任一单模块可测故障导致的状态改变可理解为四个串联的系统，每个系统的可靠性为e-cλΔt，其总概率等于e-4cλΔt。根据其两个双模可测故障导致的状态改变可理解为两个串联的系统，每个系统的可靠性为e-cβΔt，其总概率等于e-2cβΔt。这两种可测故障又可看出一个串联系统，发生任意一种都会导致状态改变。最终由状态0到状态1的总概率为1-（e-2cβΔt，e-4cλΔt），由于其Δt很小，Pij（t）（i=0，j=1）可简化为（4cλ+2cβ）Δt。同理得出系统各个状态之间的齐次马尔可夫转移概率Pij。

记Pij（t）是齐次马尔可夫过程的转移概率，qii，qij为转移密度，定义为

结合式（3）和式（4）可得其转移密度矩阵A

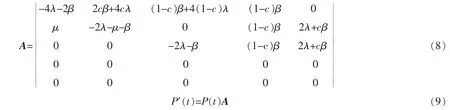
利用柯尔莫哥洛夫向前方程也即式（9）将求解马尔可夫链转移概率的问题转变为求解矩阵微分方程的问题。再利用MATLAB求解矩阵微分方程，得出各个状态在t时刻的概率P（t）。从而求得该系统的可靠度R（t）和安全度S（t），其中Px（t）中x代表状态序号，在传统工作策略下除状态3之外都属于输出安全状态，除状态3和状态4之外的状态都属于结果可靠状态。有

2.2 新降级工作策略下的状态转换马尔可夫模型

分析各状态之间的转移原理，图5中详细地标明了各状态之间转换的转移概率。以下是部分状态之间转移的含义。

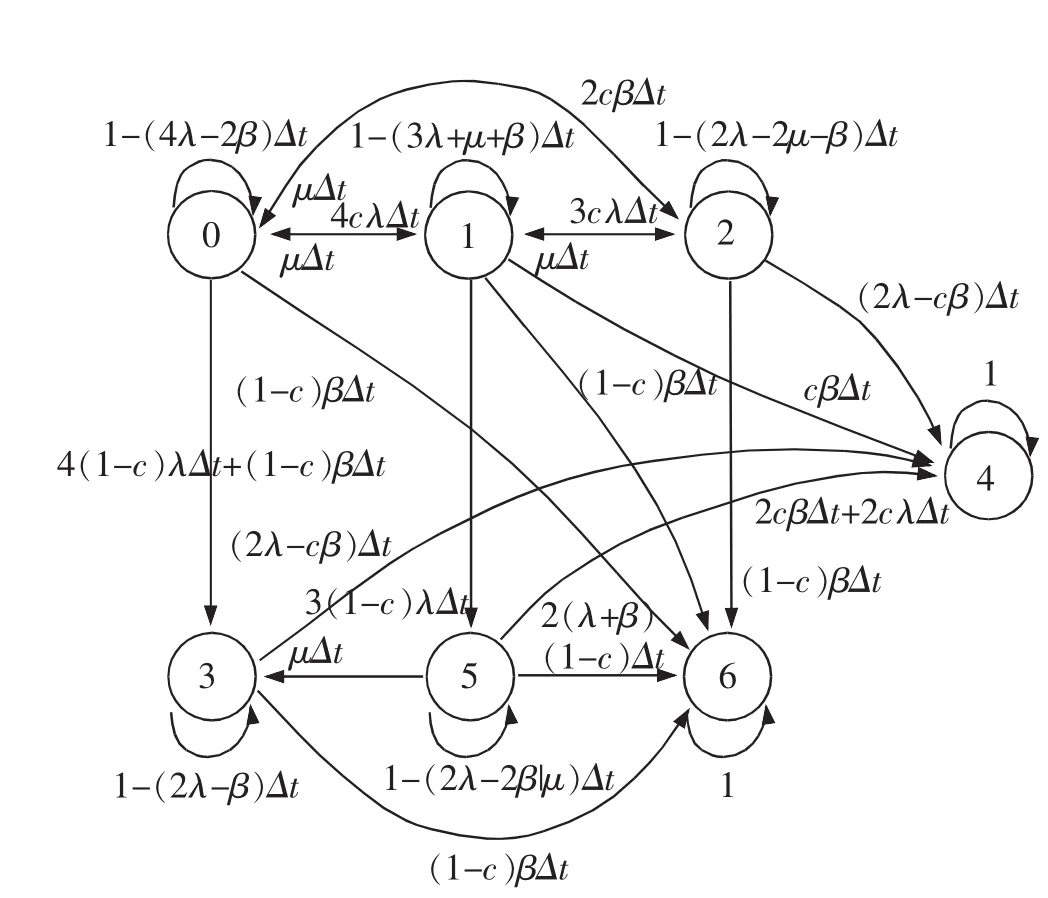
图5 新降级策略下二乘二取二系统状态转换图Fig.5 Markov state transition of double 2-out-of-2 system based on new degradation

1）0→1：二乘二取二中任一可测单模故障导向三取二。

2）0→2：二乘二取二中任一系发生可测双模故障导向二取二。

3）0→3：二乘二取二中任一系发生不可测单模故障和主系不可测双模故障导向二取二，二乘二取二中发生单模不可测故障时，不能自检出具体哪个模块故障，只能默认该系出故障，发生双模主系可测故障时，其总线表决或硬件表决器能检出故障系，使得导向二取二。

4）0→6：二乘二取二中主系发生不可测双模故障导向故障-危险。

5）1→2：三取二中发生任一可测单模故障导向二取二。

6）3→4：不可修复的二取二发生单模故障和可测双模故障导向故障-安全。

7）5→3：不可修复的三取二只是其中不可测故障单元不可修复，当二乘二取二转移至三取二时的可测故障又重新修复时，导致5状态转为0状态，但是由于还有不可测故障，又导向至3状态。

8）5→4：不可修复三取二状态下发生双模或三模可测故障导向故障-安全，发生单模故障则转移至状态3（二取二），但是由于存在未检测单模故障，立即转向安全侧。

9）5→6：不可修复三取二状态下发生未检测双模故障或三模故障系统导向故障-危险。当发生未检测单模故障时，和另一未检测单模（1-5状态时产生）共同组成未检测双模故障，同样导向故障-危险。

由于存在二取二点对点通信系内表决和总线表决或其他方式的硬件表决器。安全冗余结构下的未检测故障并非没有发现系统故障，而是发现故障时不能确定其故障模块是系内哪一个模块，且不可修复。

结合式（6），式（7）和图5推出其转移密度矩阵A，并根据转移密度矩阵每行元素相加等于0的特性验证其转移密度矩阵A是否正确。

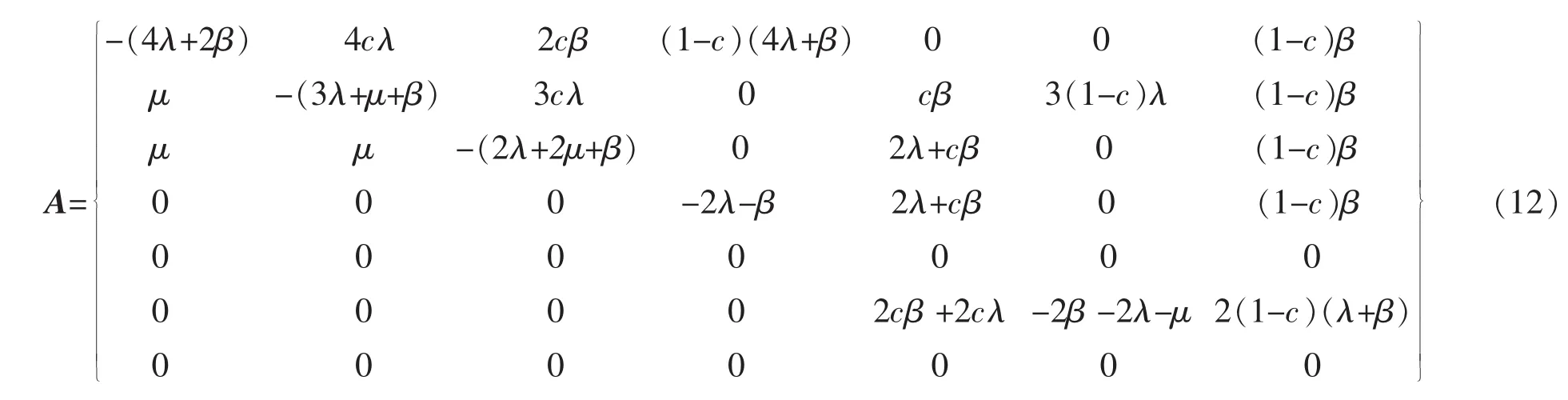
2.3 仿真结果与分析

使用MATLAB对式（9）进行编程求解。假设系统的单模故障率为0.000 1次/h，共模故障率β为0.000 1次/h,模块维修率μ=0.01次/h，故障检测覆盖率c为0.99，运行时间为5 000h。考察在相同的条件下2种不同的工作策略下的系统在可靠性上和安全性上优劣，利用MATLAB求解式（9），结果代入式（10）和式（11），将不同策略下的可靠性和安全性进行比较，其可靠性比较结果如图6，安全度比较结果如图7。

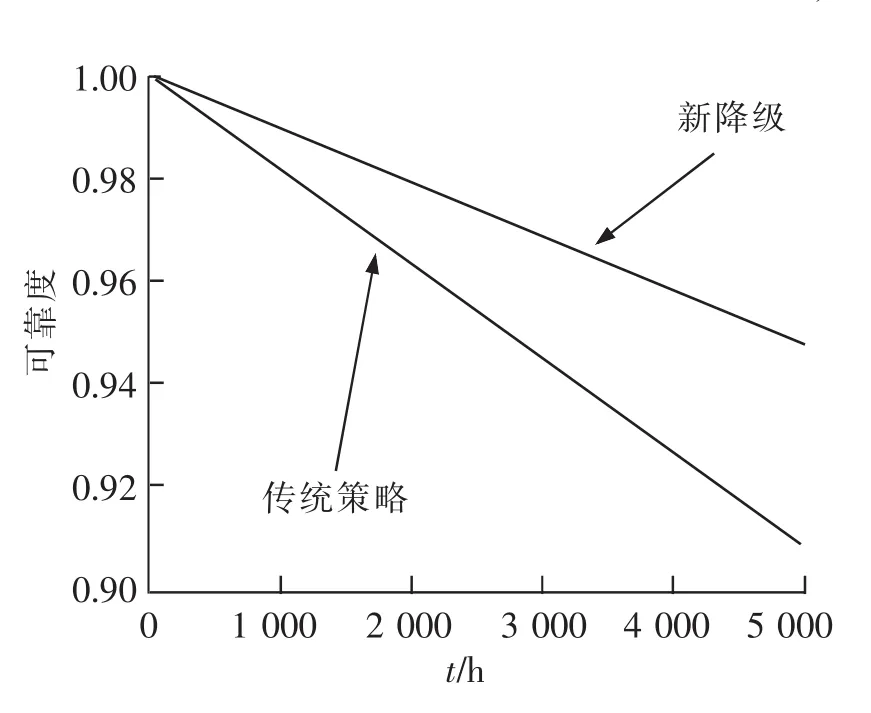
图6 可靠度对比图Fig.6 Reliability of system s

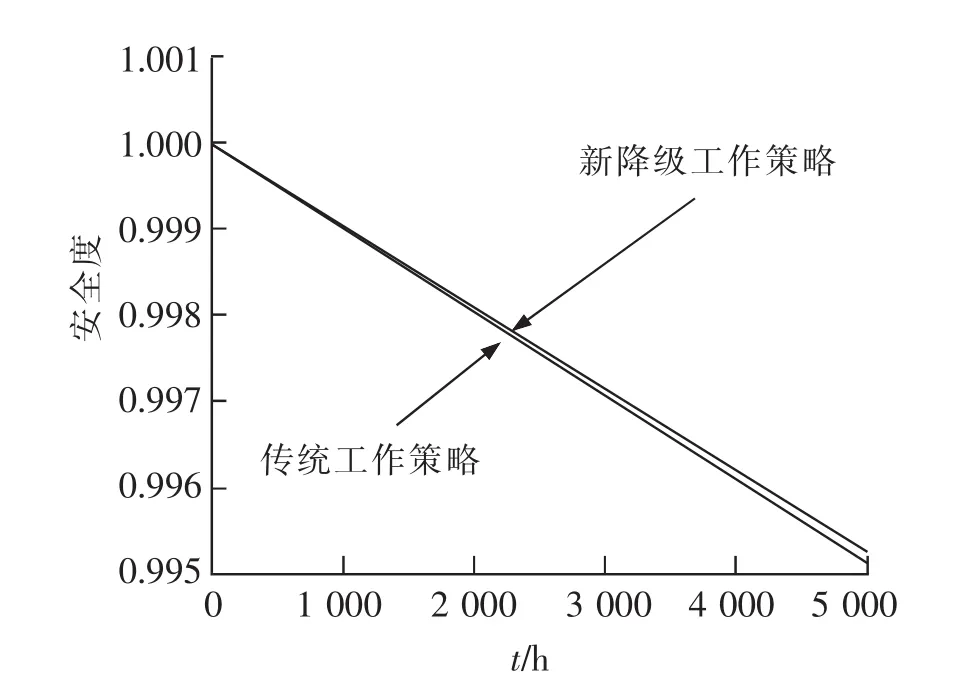
图7 安全度对比图Fig.7 Safety of systems

图6表明新降级工作策略下的二乘二取二系统可靠性比传统工作策略下的二乘二取二系统高，这主要是由于新工作策略比传统工作策略上多了一层三取二的高安全可靠过渡段，提高了整体的可靠性。从图7中可知，两种工作策略在安全性上没有明显差别。

3 结论

本文研究了二乘二取二系统的基本工作策略和结构，提出了一种基于总线表决的二乘二取二新降级工作策略，新降级工作策略同时带来了三模故障的情况发生。有必要在考虑多模故障的情况下建立其马尔可夫模型，使用MATLAB对其进行微分方程求解，并与传统工作策略的二乘二取二系统的安全度以及可靠度进行对比研究。当故障识别能力相同以及其他可影响可靠性和安全性的条件一致时，新降级工作策略下的二乘二取二冗余系统的可靠性优于传统二乘二取二冗余系统，安全性没有明显差别。所设计的新降级工作策略为提高二乘二取二冗余结构的可靠性提供一种新的解决思路。

[1]刘立月.GNSS列车定位有效性及安全完整性研究[J].华东交通大学学报，2014，31（1）：39-43.

[2]刘真.一种三取二安全计算机系统的设计与实现[J].铁路计算机应用，2016，25（11）：49-52.

[3]黄波，曹帮林，张福鑫，等.一种三模混合冗余总线控制系统设计研究[J].航天控制，2015，33（6）：76-80.

[4]程诗佳，张丹红，戈乐，等.计算机联锁系统中可靠冗余结构的研究[J].工业控制计算机，2016，29（8）：78-79.

[5]王芃，刘剑，李博.二乘二取二系统的安全性与可靠性分析[J].铁道通信信号，2013，49（S1）：104-105.

[6]孙怀义，刘斌，曹晓莉.表决冗余系统可靠性与安全性研究[J].电子测量与仪器学报，2011，25（7）：661-664.

[7]陈州，倪明.三模冗余系统的可靠性与安全性分析[J].计算机工程，2012，38（14）：239-241.

[8]DWYER V M.Reliability of various 2-out-of-4：G redundant systemswithminimal repair[J].IEEE Transactions on Reliability，2012，61（1）：170-179.

[9]张本宏，陆阳，韩江洪，等.二乘二取二冗余系统的可靠性和安全性分析[J].系统仿真学报，2009，21（1）：256-261.

[10]方云根，曾小清，王刚.轨道交通列控系统共因失效分析[J].上海交通大学学报，2015，49（7）：1052-1057.

[11]张文韬，张友鹏，苏宏升，等.基于动态故障树的CTCS-3级ATP系统可靠性分析[J].工程设计学报，2014，21（1）：18-26

[12]杨其国.基于Markov过程的冗余系统可靠性分析[J].计算机仿真，2011，28（1）：356-359.

New Degradation Strategy of Double 2-out-of-2 System

Zhang Yongxian，Zou Libang，Wu Wenjie，Liao Zhaocong
（School of Electrical and Automation Engineering，East China Jiaotong University，Nanchang 30013，China）

With rapid development of railway in China,safety and reliability of systemshave been paidmore andmore attention.In order to improve the reliability and safety of double 2-out-of-2 system which is widely used in railway vital computers，the reliability of several commonly used redundant architectureswere analyzed and a new degradation strategy was proposed based on the analysis of the architecture of double 2-out-of-2 and 2-out-of-3.In the case of simultaneous failure ofmultiplemodules,the working strategy and the transition of all states of the system were analyzed，and the Markov state transitionmodel was established.Its reliability and safety were evaluated by MATLAB.Compared with the traditional double 2-out-of-2 system，the new degradation strategy systemhashigher reliability.

double 2-out-of-2；reliability；safety；multiplemodule failure；Markovmodel

1005-0523（2017）05-0099-07

U284.3；TP39

A

2017－04－19

江西省教育厅科学技术研究项目（GJJ160496）；华东交通大学校立科研基金（14DQ06）

张永贤（1975—），男，副教授，研究方向为轨道交通控制与安全。

（责任编辑 姜红贵）