基于Stackelberg博弈的车-网双向互动策略研究
程宏波,李明慧
(华东交通大学电气与自动化工程学院,江西 南昌 330013)
基于Stackelberg博弈的车-网双向互动策略研究
程宏波,李明慧
(华东交通大学电气与自动化工程学院,江西 南昌 330013)
电动汽车与电网之间可实现能量的双向流动,这种双向互动将是智能电网研究的一个重要内容。车网互动双方利益有冲突、决策有先后,具有动态博弈的特点。在分析车网互动的形式及特点的基础上,利用Stackelberg动态博弈理论分析双方利益的均衡问题,建立电动汽车和电网的博弈模型,结合优化算法对此博弈模型进行求解得出納什均衡解,对车网双方交易电价及电价基础上的充放电电量进行分析,确定车网的互动策略。以某一地区电动汽车的使用情况和电网公司的负荷状况为例进行了分析计算,结果表明方法得出的交易电价和电动汽车的充放电电量在减小用户用车成本的同时,对电网负荷起到削峰填谷的作用,可以实现电网公司和用户双方利益均衡。
交易电价;充放电方案;动态博弈;納什均衡;削峰填谷
随着能源危机的加深及大气污染的加剧,节能和减排成为未来汽车技术发展的主攻方向。根据工业和信息化部《电动汽车发展战略研究报告》预测,2030年我国电动汽车保有量将达6 000万辆,同时充电峰值功率将达到全国总装机容量的26%[1]。在无经济利益和政策引导的情况下,大规模电动汽车无约束的充电势必会对配电网的运行、规划等方面产生巨大的影响。因此,促进电动汽车与电网的双向互动,利用合理电价引导电动汽车有序充放电,在电网峰荷时段向电网输送电能,电网低谷期间由电网向电动汽车的车载电池充电,可以降低电网的峰谷差,提高发电设备的综合利用率,起到节能减排效果。
电动汽车与电网的互动过程中,在市场经济环境下双方都希望实现自身利益的最大化。但双方的利益之间存在着竞争性,双方所选择的互动策略会影响双方各自的收益,因而形成一个相互博弈的过程:电网公司、电动汽车(用户)是参与博弈的主体,电动汽车的充放电电价以及与之对应的充放电电量则是博弈形成的策略集合。同时,电网与电动汽车的充放电电价会根据供需关系和电网的峰谷情况而调整,电动汽车的充放电行为又会受到电网定价的影响,可见双方的策略是相互影响、相互制约的。由此可见,车网互动策略的研究必须要考虑到互动过程中双方的利益博弈问题。车网互动过程中,电动汽车与电网之间的经济利益通过电价体现,交易电价是引导电动汽车与电网互动的直接手段。交易电价及依据电价确定的充放电方案是车网互动研究的主要问题。因此研究基于实时电价的互动博弈具有重要意义。电力市场中研究定价问题时,有利用静态贝叶斯博弈中的拍卖模型分析不同发电企业之间的竞价上网问题[2-3],也有利用动态贝叶斯博弈分析电力用户与发电商的购电定价问题,通过动态贝叶斯博弈多轮报价改进自身博弈效用,提高双方博弈效率[4]。此外还有各微网间通过互动博弈来确定自己的投标价格及电量,以获取合理的利益并降低运行成本[5],运用斯坦克尔伯格博弈模型分析电力零售商间收益及定价问题,通过采用动态博弈理论分析服务不同类型用户的不同零售商间策略互动对实时电价的影响,较好地体现未来电力市场中多零售商间动态实时定价的过程[6]。文献[7]针对智能电网中几个典型的主从博弈问题,分析主从博弈的数学模型,并给出了相应的求解算法。文献[8]采用Stackelberg博弈建立发电厂和大用户等效电能定价间的博弈模型,分析了各参与方收益均衡的定价策略。可见电力市场中的定价博弈问题已有一些研究成果,但车网互动的博弈主体及其特点不同,上述博弈方法不一定能简单的套用。
也有部分文献利用博弈理论分析了电动汽车参与电力市场时的定价问题。文献[9-11]分析了影响电动汽车充放电电价的因素,从政府相关政策、边际运营成本和电动汽车数量3个方面,通过博弈分析比较得出电网、政府、用户三方收益最大时的定价策略。文献[12]利用静态贝叶斯博弈中的双向拍卖模型制定电动汽车与电网的交易电价及电量,得出使电动汽车与电网两方效用函数最大的交易电价及电量。但在分析的时候没有考虑电动汽车负荷的“削峰填谷”效应,需做进一步深入研究。文献[13]则在智能小区中,设置对多辆电动汽车进行分散管理的代理商,分析了代理商与电动汽车车主利益的优化问题。文献[14]运用Stackelberg博弈建立电网公司与用户的双层优化模型,分析了满足电网公司收益最大和用户用电成本最小的放电电价的制定,但没有给出充电电价的制定方案。
在电动汽车与电网的互动过程中,电网公司往往是双方交易电价制定的主要角色。一般电网公司先确定一个电价,电动汽车用户再对电网公司确定的电价作出响应,确定充放电量以使自己的利益最大化。在实际的互动中,电动汽车用户的充放电决策又会反过来影响电网公司对交易电价的制定,以此两者反复博弈,最终形成动态均衡。因而在实际的互动中,电网公司为上级决策者,用户为下层决策者,它们之间的行为有先后,且一方的策略选择会对另一方的收益产生直接的影响。斯坦克尔伯格(Stackelberg)模型属于非合作的动态博弈模型[15],与车网互动过程中的上述特点较为一致。
本文利用Stackelberg博弈模型分析电动汽车与电网的互动问题,建立以电网公司与电动汽车用户收益最大为目标的动态博弈模型,在此基础上利用微分进化算法进行求解,确定双方互动中实时充放电电价及电量的制定决策。该决策能够平衡和优化互动双方的利益,为电网公司电价制定及电动汽车充放电决策提供有益参考。
1 车网互动的Stackelberg博弈模型
车网互动的过程中,电网公司往往处于主导地位,可以先行选择行动策略,而电动汽车用户则往往根据电网的决策采取有利于自己的策略,处于从属地位。
车网互动过程中,双方决策的依据都是期望使自己的收益最大化,对于上级决策者电网公司来说,其目标为

式中:G表示电网公司收益函数;pi为电网公司的决策变量,即电网公司与电动汽车用户之间的交易电价;函数F(pi,qi)≥0表示电网公司侧决策变量所需满足的约束条件;pi∈P={pi:H(pi)≥0}表示双方交易电价的取值范围。
对于后续决策者电动汽车用户来说,其目标为

式中:V表示电动汽车收益;fi(pi,qi)≥0表示电动汽车侧的决策变量所需满足的约束条件;qi∈Q={qi:hi(qi)≥0}表示电动汽车充放电量约束。
互动中,电网公司首先根据自身运行情况及负荷预测信息确定一个初始电价P1及在此报价下期望用户的充(放)电量Q1。用户接收到报价P1后,根据自身的用电需求作出充放电决策Q2并上报电网公司。当电动汽车的电池荷电状态正好满足用户的行车需求时,用户一般不进行充(放)电;当电动汽车电池荷电状态低于或高于用户的用电需求时,用户可进行充电或放电。当时,可视为用户接受电网公司这一报价P1,报价P1将作为该时段的定价策略。当Q2 双方互动过程中,收益始终是双方博弈的关键所在。双方博弈的目的都是希望自己的收益最大,因此确定影响电网公司与电动汽车用户收益的因素,并据此确定合适的收益函数是进行博弈分析的前提。 为简化处理,本文将电动汽车充电站的收益划归电网公司所有。从互动两方考虑,影响电网公司收益的因素包括充电电价、放电电价、电动汽车充电功率、放电功率、电源及电网的投资成本等。另外还要注意使系统充电负荷平滑,同时还需满足电网越限频率的限制条件。 以电网公司制定的实时电价为决策变量,根据上述影响因素列出电网公司的收益函数: 式中:Pc为电动汽车24h充电电价;Qc为电动汽车24h充电电量;ηc为电动汽车充电效率;Pd为电动汽车24h放电电价;Qd为电动汽车24h放电电量;ηd为电动汽车放电效率;N为智能充电桩的数量;E为单位容量的电源及其电网建设成本;Fp为车网互动带来的峰荷降低量;j为利率;m为电源及电网的使用周期;j(1+ j)m/(1+j)m-1为通过电动汽车充放电,电网得到的削峰填谷效益转换为等年值的系数。 同时考虑系统负荷最平滑时的目标函数为 式中:L表示系统负荷方差;Ll,i为i时段系统负荷;Nqc,i为i时段电动汽车总充电功率;qc,i为Qc的i时段元素;Nqd,i为i时段电动汽车总放电功率;qd,i为Qd的i时段元素;Lav为系统平均负荷。 大规模电动汽车充电势必会对电网造成冲击,当电网容量不足时,很可能发生瞬时频率越限,所以电动汽车充电时必须考虑电网的容量,需要确保电网不会有低频减载情况的发生。其满足的约束条件为 式中:Δf为允许最大频率越限;f为电网频率;Pw为电网总功率。 智能电网信息流的双向流动,使得电动汽车用户及时获取电网公司充放电电价成为可能,电动汽车用户能够对电网公司的电价做出及时响应。影响电动汽车收益的因素有电动汽车的充电电量、放电电量、充电电价、放电电价、电池损耗及电池充放电效率。据此列出电动汽车用户侧收益函数为 式中:Pd为电动汽车24h放电电价;Qd为电动汽车24h放电电量;ηd为电动汽车放电效率;Pc为电动汽车24h充电电价;Qc为电动汽车24h充电电量;ηc为电动汽车充电效率;S2为单位充电量造成的电池损耗;S1为单位放电量造成的电池损耗;N为智能充电桩的数量,为了便于计算,本文假设用于充电和放电的充电桩数量均为N。 电动汽车用户通过改变电动汽车的充放电电量来对电网公司的电价做出响应,即电网公司电价的调整会影响用户的充放电电量。用户的充放电行为反过来影响电网公司的最优电价的制定。考虑到电价弹性,充电电价变化引起用户充电量的变化关系可表示为 式中:Ti为第i个充电时间段的充电时间;自弹性系数εii的求取是根据文献[17]中所讨论的方法来计算的。充电时间约束0≤Ti≤1。 同理,放电电价变化引起用户放电量的变化关系可表示为 式中:Ti′为第i个放电时间段的放电时间;自弹性系数εii′的求取是根据文献[17]中所讨论的方法来计算的。放电时间0≤Ti′≤1。 为激发车网双方参与互动的积极性,均衡各方利益,博弈双方的收益都应考虑最大化。由于双方收益函数涉及的变量较多,必须选取合适的优化算法对其进行求解。分析电动汽车用户及电网公司的目标函数,属于多目标优化问题,可利用多目标微分进化改进算法对其求解,因为多目标微分进化改进算法具有很高的处理多目标优化问题的效率及很强的寻优能力,能快速地求解此多变量问题。算法流程如图1所示。 图1 模型求解算法流程图Fig.1 Flow chart of themodel’s algorithm 本文以某地区电动汽车的使用情况为例进行分析,验证所提模型的可行性。设定该地区智能充电桩的数量7 000个,电动汽车选取纯电动汽车,电池容量为57 kW·h。纯电动汽车充放电效率ηc=ηd=0.97,电动汽车为锂离子电池,恒功率充电,假设智能充电桩的充放电功率均为10 kW。单位充放电量造成的电池损耗S1=S3= 0.43元/(kW·h)。电动汽车每天出行情况为早上8∶00—9∶00;晚上17∶00—18∶00。已知单位负荷对应的电源及电网投资成本E=14 847元/kW,利率j=10%,电源及电网的使用周期m=30,该地区的一日电网基础负荷数据如表1所示。 表1 该地区一日每时段日负荷数据Tab.1 Real-time load data for one day in the area MW 求解博弈均衡解过程中,电网公司和电动汽车的动态博弈过程:首先由电网公司产生满足基本约束条件的初始电价,电动汽车对此电价反馈一个满足约束条件的充放电电量,将电价及电量初始值代入双方收益函数值,判断计算结果是否满足电网及电动汽车侧收益最大的均衡条件。若不满足,对电价进行重新赋值,电动汽车在考虑价格及自身需求的情况下给出此价格下的充放电量,将此时的电价及电量重新代入双方目标函数再进行判断。重复以上过程,直到满足均衡条件,博弈过程结束,最后得出的4组变量值即为所求的均衡解。对此算例求解得出峰荷降低量Fp=140 MW,电网侧收益为750 990元,电动汽车用户群的用电成本最小为437 050元。 在均衡解情况下求得的充电桩一天中每时段充放电定价策略如表2所示。该充放电电价与电网常规负荷变化之间的关系如图2所示,从图中可以看出各时段的充放电电价与电网的负荷之间存在着一定的对应关系:电网用电高峰时段,充放电电价都较高,一方面可以抑制电动汽车的充电需求,避免电动汽车充电对负荷高峰的叠加;另一方面可以鼓励电动汽车在负荷高峰时对电网放电,为电网提供足够的功率支撑。在用电低谷时段,充放电电价都较低,一方面可以鼓励电动汽车在此时充电,避免电能的浪费;另一方面可避免电动汽车向电网放电。 可以看到,出于负荷控制的需要,电动汽车充放电电价受电网基础负荷的影响较大,基本上随电网负荷的波动而波动。 表2 电网侧各时段定价策略Tab.2 Real-time pricing strategies of power grid 图2 电网常规负荷及电网公司定价策略图Fig.2 Schematic diagrams of the grid’s constant load and pricing strategies 在对应的充放电电价下,电动汽车用户会结合自身的使用需求,产生相应的充放电策略。分析电动汽车用户群在充电桩上每时段的充放电情况,此充放电时间是对不同充放电电价的响应,电动汽车用户可按此充放电策略安排充放电时间,其中充电状态为0表示在此时刻不进行充电,充电状态为1表示在此时刻进行充电。将电动汽车充电时段及放电时段与电网基础负荷变化情况进行对比分析如图3所示。图中可以看出,电网基础负荷高峰时段,电动汽车充电状态为0,表示不进行充电,充电避开了负荷用电高峰期;而在基础负荷低谷时段,电动汽车充电状态为1,电动汽车在此时进行充电,避免了谷电资源的浪费。这样可对电网负荷起到“削峰填谷”的作用,同时峰谷电价的差值,可为电动汽车参与互动带来一定的经济性。 电动汽车参与前后电网负荷的变化特性如图4所示。从图中可以看出在电动汽车不参与互动时,该地区电网常规负荷峰谷差达到800MW。电动汽车按表2所示策略参与互动后,电网负荷峰值从原来的1 500MW减小到1 430MW,电网负荷低谷值从原来的700 MW增加到770MW,负荷峰谷差减小为660 MW。起到了较好削峰填谷的作用。且电动汽车接入后电网负荷的方差由原来的50 191 MW2减小到35 614 MW2,可见负荷的平滑性得到较好的改善。 图3 电动汽车充放电时段与电网常规负荷对比图Fig.3 Contrast between the electrical vehicle discharge load and the grid’s constant load 图4 电动汽车入网前后电网供电负荷特性Fig.4 Contrast diagram s of power supply load in preand-post periods of electrical vehicle joining power grid 通过建立Stackelberg博弈模型分析车网互动策略,车网双方可通过充放电电价及对此电价响应的充放电量进行互动。以互动双方收益最大为目标函数,并结合优化算法对博弈问题进行求解,得出满足互动双方收益最大的均衡解,从而得到双方每时段交易电价及电动汽车每时段的充放电策略。对于电网公司来说,按此策略制定交易电价,不但可以增加售电量,获得一定的收益;还可以通过此电价合理引导电动汽车充放电,在一定程度上减小电网供电的压力,从而减小电网建设投资费用。对于电动汽车用户来说,此充放电策略可以降低用户的用电成本。此外通过分析电动汽车每时段充放电时间与电网每时段基础负荷对比图可知电动汽车的充放电对系统负荷起到“削峰填谷”的作用,从而提高电网运行的稳定性。可见此互动策略能够很好地促进电动汽车与电网的良性互动。在电动汽车充分发展的将来,电动汽车的充放电将被统一部署,根据既定的车网互动策略,电动汽车用户和电网企业将获得双赢。 [1]李正烁,孙宏斌,郭庆来,等.计及碳排放的输电网侧“风—车协调”研究[J].中国电机工程学报,2012,32(10):41-48. [2]SAEED RAHMANIDABBAGH.Risk-based profit allocation to DERs integrated with a virtual power plant using cooperative game theory[J].Electric Power Systems Research,2015,121(2):368-378. [3]W ANG Y.Interactive dispatchmodes and bidding strategy ofmultiple virtual power plants based on demand response and game theory[J].IEEE Transactions on SmartGrid,2016,7(1):510-519. [4]谭忠富,柏慧,李莉,等.电力用户从发电商购电定价的双边贝叶斯动态博弈学习模型[J].华东电力,2009,37(3):384-388. [5]江润洲,邱晓燕,李丹.基于多代理的多微网智能配电网动态博弈模型[J].电网技术,2014,38(12):3321-3327. [6]代业明,高岩.基于智能电网需求侧管理的多零售商实时定价策略[J].中国电机工程学报,2014(25):4244-4249. [7]梅生伟.智能电网环境下主从博弈模型及应用实例[J].系统科学与数学,2014,34(11):1331-1344. [8]夏炜.直购电交易中等效电能双边定价博弈研究[J].现代电力,2015,32(3):71-75. [9]W ANG Y,A I X,Y AN L,etal.A game-theoreticmode for EV discharging price and its application[C]//IEEE Conference and Expo Transportation Electrification Asin-Pacific,IEEE Conference Publication,2014:1-4. [10]W ALID S AAD.Game-theoreticmethods for the smart grid:an overview ofmicrogrid systems,demand-sidemanagement,and smartgrid communications[J].IEEE Signal Processing Magazine,2012,29(5):86-105. [11]S AAD W,H AN Z,P OOR H V,et al.A noncooperative game for double auction-based energy trading between PHEVs and distribution grids[C]//IEEE International Conference on Smart Grid Communications,IEEE Conference Publications,2011:267-272. [12]孙波,王振兴,赵文会,等.基于静态贝叶斯博弈的电动汽车放电电价分析[J].可再生能源,2015,33(11):1686-1692. [13]魏韡,陈珗,刘锋,等.基于主从博弈的智能小区代理商定价策略及电动汽车充电管理[J].电网技术,2015(4):939-945. [14]李成伟.基于博弈论的电动汽车放电电价研究[J].华东电力,2013,41(6):1329-1334. [15]盛昭瀚.主从递阶决策论-STACKELBERG问题[M].北京:科学出版社,1998:370-393. [16]覃鹏,王正,单晓芳,等.信号交叉口人车通行博弈分析[J].华东交通大学学报,2016,33(2):93-99. [17]秦祯芳,岳顺民,余贻鑫,等.零售端电力市场中的电量电价弹性矩阵[J].电力系统自动化,2004,28(5):16-19. Study on Bilateral Interaction Between Vehicle and Grid Based on Stackelberg Model Cheng Hongbo,LiMinghui The implementation of bidirectional energy flow between electric vehicles and grid is an important research on smart grid.Vehicle-to-grid interaction is characterized by dynamic game for the interest conflicts and priority decisions.Based on the specific form and characteristics of vehicle-to-grid interaction,the equilibrium problem ofmutual interestwas analyzed by the Stackelberg dynamic game theory and the vehicle-to-grid gamemodel was also established.By using optimization algorithm,solution of Nash Equilibrium was gained from thismodel.Then,this paper analyzed the vehicle-to-grid power exchange and charge-and-discharge energy based on power exchange.Finally,the vehicle-to-grid interaction strategieswere explored through analysis of vehicleto-grid power exchange as well as charge and discharge.Taking a specific area as the object,this paper analyzed its electric-vehicle usage frequency and power-grid company loading conditions.Research results show that the proposed strategy can not onlyminimize the users’cost,but also play a role in peak load shifting,which achieves the benefit equilibrium between power grid companies and users. power exchange;charge-and-discharge scheme;dynamic game;Nash Equilibrium;peak load shifting 1005-0523(2017)05-0049-07 TM761 A 2017-04-27 国家自然科学基金项目(51667008) 程宏波(1979—),男,副教授,博士,研究方向为电网的智能控制及供变电设备的状态监测及故障预警。 (责任编辑 刘棉玲)2 车网互动的收益分析
2.1 电网公司收益

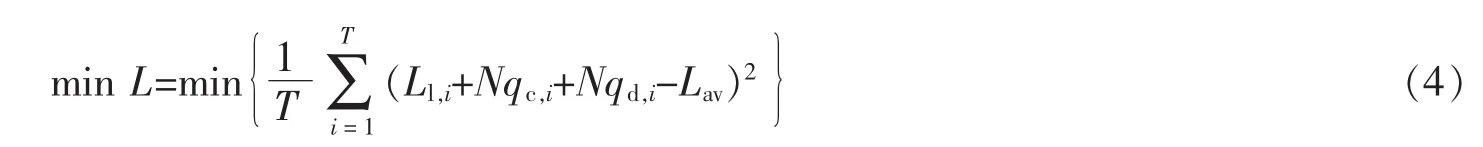

2.2 电动汽车用户收益

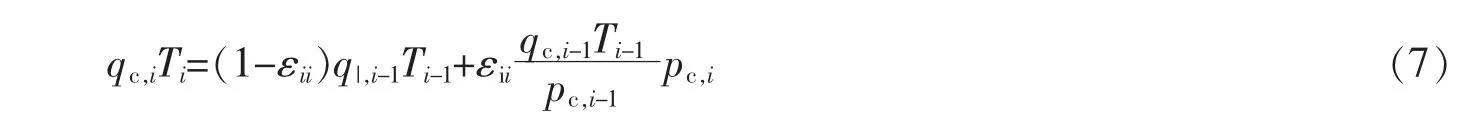
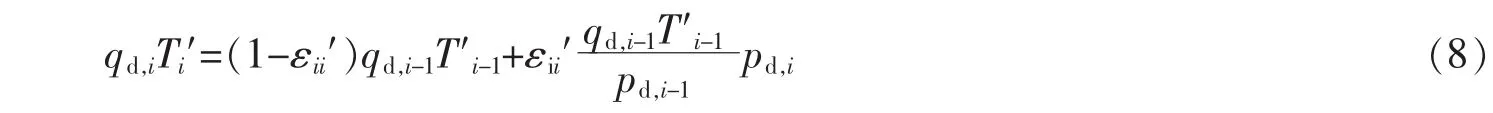
3 车网博弈均衡解的求解方法

4 算例分析
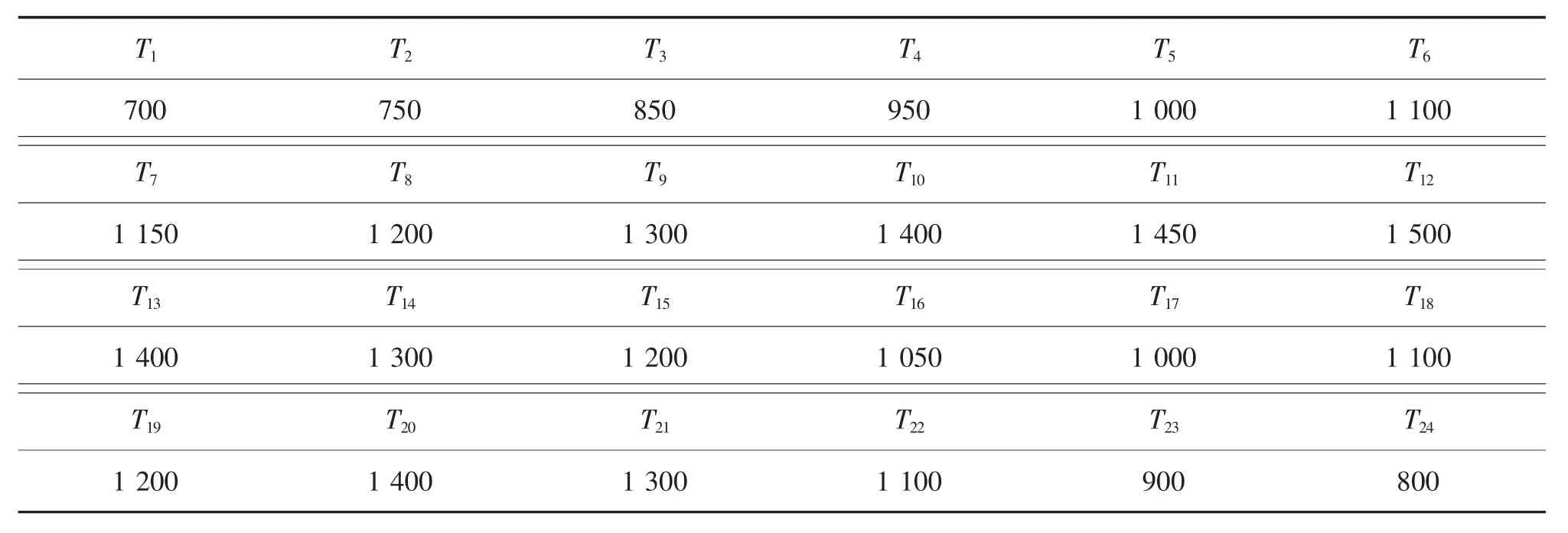
4.1 电网公司的定价策略分析


4.2 电动汽车用户群的充放电策略分析
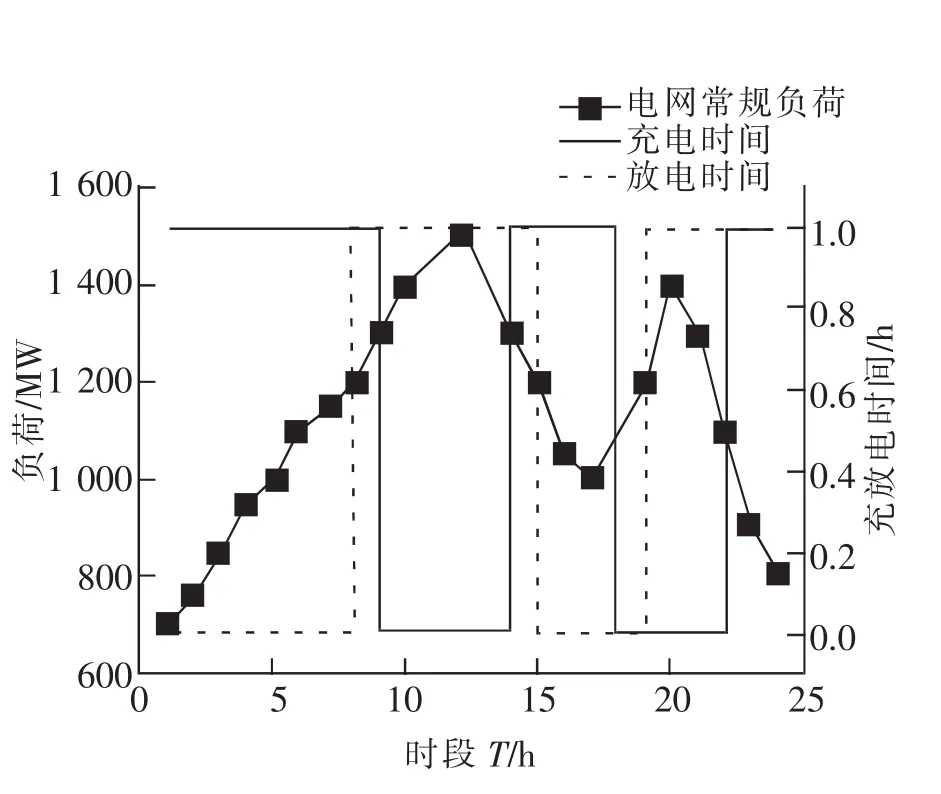
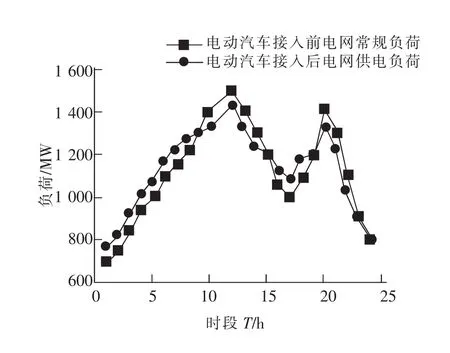
5 结论
(School of Electrical and Automation Engineering,East China Jiaotong University,Nanchang 330013,China)

