Matlab下永磁同步电机的三相坐标系建模

陈文卓，靳文涛

(华北科技学院 电子信息工程学院，北京 东燕郊 065201)

Matlab下永磁同步电机的三相坐标系建模

陈文卓，靳文涛

(华北科技学院 电子信息工程学院，北京 东燕郊 065201)

目前永磁同步电机本体的建模存在不足，一方面,MatlabSimulink中的PMSM模块采用的坐标系非国内通用标准坐标系，且其集成性高，不便于根据实际修改参数；另一方面,自定义电机模型大多基于坐标转换进行搭建，普遍使用两相输入，与实际生产中广泛应用三相电输入的情况不符。因此针对三相静止坐标系下的PMSM建模进行研究，从电机三相定子电压方程出发，结合坐标转换矩阵，通过分析直轴电感和交轴电感之间的关系合理简化磁链方程，推导出三相静止坐标系下的磁链关系，并结合电机运动方程、电磁转矩方程得到三相坐标系下电机的数学模型。在此基础上结合实验仿真，证明了模型的正确性和有效性。

永磁同步电机；三相坐标系；Matlab；建模

0 引言

永磁同步电机(Permanent Magnetic Synchronous Motor, PMSM) 由于没有励磁电流，具有高效率和高功率因数等优点；同时PMSM的转子参数可测，定子电流和定子电阻损耗减小，使得其控制系统能够实现高精度、高动态性能、大范围的调速和定位控制[1-3]。然而PMSM控制系统是一个具有非线性、强耦合性和时变性的复杂系统，其在运行过程中会受到不确定因素的影响而使参数产生不可预见的变化，为了对比验证各种控制策略和算法的正确性和优越性，使之更好地应用在工程实际中，要求针对PMSM本体的模型要必须简单实用，且具有一定的扩展性。

目前在PMSM建模研究方面，何杰为实现永磁同步电动机(PMSM)的电压空间矢量控制,在分析永磁同步电动机数学模型的基础上,利用Matlab/Simulink建立了永磁同步电动机矢量控制系统的仿真模型[4]。张红生为了更好地实现永磁同步电机的矢量控制，在永磁同步电机的电压、电流、磁链关系表达式基础上，运用MATLAB结合Park和Clarke变换建立了PMSM的两相数学仿真模型，并对其进行了验证[5]。李平在深入分析永磁同步电机的电磁特性后，推导出永磁同步电机在两相静止坐标下的电机数学模型，并在该数学模型下利用递推最小二乘法编写辨识算法，对电机的参数进行在线辨识[6]。陈俊硕用电机的AR模型为内部模型，对传统模型中的系数进行优化，克服了传统模型算法需要选择较长的采样周期计算控制量的缺点，能很好地满足动态较快的电动机实时性要求[7]。

以上研究中所使用的PMSM模块多为MatlabSimulink中所提供封装好的库文件模块和自定义的两相输入模型。前者使用的库文件模块受其集成性限制，不能方便灵活的修改参数和进行功能扩展，且坐标定义与国内标准不符，不便于进行研究；自定义模型通常需要将整流的三相输出变量通过Clarke变换转换为两相旋转坐标系下的两相输入变量，与实际的电机应用情况不符。因此，本文基于永磁同步电机的基本电磁关系, 推导出三相定子电压及磁链方程矩阵,并在此基础上建立了三相坐标系下的自定义PMSM仿真模型，通过对运行数据对比分析，证明了所设计模型的正确性。

1 PMSM物理模型

目前国内通用的永磁同步电机物理模型如图1所示，三相静止坐标系(ABC坐标系)，两相静止坐标系(αβ坐标系)和两相旋转坐标系(dq坐标系)是永磁同步电机控制系统在模型搭建过程中使用到的三种坐标系。

考虑到永磁同步电机电磁关系的复杂性，首先做出如下假设：定子绕组Y形连接，各绕组轴线在空间上互差120°，其相反电动势波形为理想正弦，且忽略磁场高次谐波的影响；转子永磁体产生主磁场，没有阻尼绕组，其工作时转子永磁体磁链为一固定常数；忽略电机的铁心饱和，同时忽略定子铁心与转子铁心损耗和磁滞损耗[8]。根据前述假设条件，PMSM三相定子绕组对称分布，规定A、B、C分别为三相绕组的首端，X、Y、Z分别为尾端，各相绕组中电流的正方向为从首端流出，尾端流入。此时定子绕组产生磁场的方向根据右手螺旋定则规定为该相绕组轴线的正方向，可以建立一个三相静止坐标系ABC坐标系，定子三相绕组轴线固定在定子绕组上，是静止不动的，其相位在空间上互差120°电角度。

在PMSM矢量控制系统当中，根据磁链与转矩解耦的核心，针对电机转子建立的为两相旋转坐标系(dq坐标系)，其固定在转子上，并随着转子同步旋转，d轴是沿励磁磁极的轴线分布的轴，即N极所在位置，q轴逆时针超前d轴90°电角度。当电机运转时，转子旋转角速度为ω。同时规定d轴与A轴之间的夹角为变量θ。控制系统当中的逆变环节需要建立两相静止坐标系，其中α轴重合于A轴产生磁势的方向，β轴逆时针旋转超前于α轴90°电角度。

与国内常规定义不同，在MatlabSimulink中PMSM模块坐标系规定如图2所示，角度θ在此是q轴与A轴之间的夹角，而非国内通用的d轴和A轴之间的夹角[9-11]。这种相位角的差异使得针对PMSM的Simulink相关建模当中，虽然对clarke变换没有影响，但是Park正逆变换的中间量有所不同，从而给分析研究带来不便。

图2 MatlabSimulink中永磁同步电机模块坐标系定义

2 三相坐标系模型

在先前的考虑和介绍的基础上，为统一坐标系定义，同时使PMSM的模型搭建更具通用性和实用性，从定子电压方程矩阵入手，建立三相静止坐标系下的三相输入PMSM数学模型，定子电压方程矩阵如下

(1)

(2)

其中

λq=Lqiq,λd=Ldid+λpm

(3)

(4)

将式(3)、(4)代入(2)有

(5)

其中，

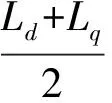
(6)

上式中，由于永磁同步电机中永磁体的厚度大于气隙长度，因此直轴磁阻大于交轴磁阻，而电感与磁阻成反比，所以交轴电感总是大于直轴电感，即Lq>Ld；且永磁同步电机的结构决定了其交直轴电感差异很小(小于10%)，因此交直轴电感可以看作近似相等，也就是L2=0[12]。综上式(5)第一项中θ相关项的影响相对较小可以忽略不计。因而在三相静止坐标系下，永磁同步电机三相坐标下定子电压方程可以简化为：

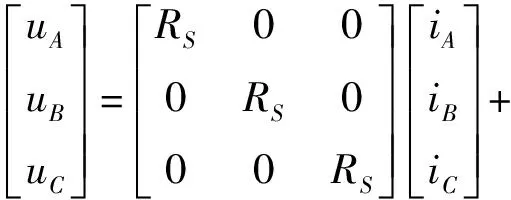
(7)

结合电机运动平衡方程式

(8)

式中为J折算到电机轴端的转动惯量，Te电磁转矩，Tl为折算到电机轴端的负载转矩，B为摩擦系数。

电磁转矩方程

(9)

其中p为永磁同步电机的极对数,λpm为转子永磁体磁场匝链到定子绕组的磁链,、iq和id分别为q轴与d轴的定子电流。

以及电机运行时，磁场储能的方程

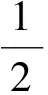
(10)

转子旋转角度θ与转子角速度ωn之间的关系满足

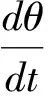
(11)

其中，ω为转子的转速[8]。

3 应用仿真

在MatlabSimulink中对比集成PMSM模型以及自定义的三相坐标系电机模型，选取永磁同步电机直接启动过程作为研究对象，其电机参数设置为：直轴电感0.0085 mH，交轴电感0.0085 mH，定子绕组电阻2.875 Ω，转子永磁体在定子绕组中产生的磁链0.175 Wb，转动惯量0.0008 kg·m2，转轴处摩擦系数为B=0，极数p=4。仿真时长为0.2 s，采用三相对称电压供电，电压幅值380 v，频率50 Hz。

图3～6分别展示了PMSM输出变量当中的定子三相电流，电磁转矩，和电机转速波形对比图。从图3和图4中可以看出，电机刚起动的短时间内(0～0.01 s)定子电流较大，经过0.01 s以后很快趋于稳定，其符合电机直接启动的理论运行状况；图5和图6显示，电机直接启动时两种模型中电机转速和电磁转矩虽然起初振荡幅度较大，但整体收敛，且最终在0.15 s以后趋于稳定，说明电机转速可以很快跟随同步角速度速度；由于建立的模型仅针对电机本体，没有施加任何控制策略，因而存在着一定程度的失步现象。同时通过对比发现，两种模型的各项输出曲线几乎重合，再次证明了自定义三相坐标系模型的正确性。

图3 自定义三相坐标系PMSM模型的三相定子电流波形图

图4 Simulink集成PMSM模型的三相定子电流波形图

图5 电磁转矩波形对比图

图6 电机转速波形对比图

4 结论

本文设计并实现了一种三相坐标系的改进PMSM建模，基于对定子三相电压矩阵的展开研究，提出了简化磁链矩阵的方法，并对所建的模型从定子三相电流、转子旋转角度，电磁转矩，转子转速和磁场储能五个方面入手，分析了PMSM的直接启动过程。相对于Simulink中的集成PMSM模型，自定义模型遵循国内研究习惯，所有变量可以在线修改，方便对电机进行深入的动态研究；集成模型采用Simpower电力库模块搭建，而自定义模型各层均采用信号模块，且为实现电机控制而采用的控制策略均以信号转换为基础，因此后者具有更好的兼容性。最后仿真结果对比显示了PMSM在未使用任何控制策略的情况下能够直接启动并最终稳定在同步转子角速度，其符合理论预期，证明了本文搭建模型的正确性。

[1] 李崇坚.交流同步电机调速系统[M].北京:科学出版社，2006:12-54，263-287.

[2] DE ALMEIDA A T，FERREIRA F J T E，FONG J A C.Stand-ards for efficiency of electric motors[J].IEEE Industry Applications Magazine，2011，17(1):12-19.

[3] THOMAS H, ENNO L, KAY H, System Simulation of a PMSM Servo Drive Using Field-Circuit Coupling[J] IEEE Transactions on Magnetics,2011,47(5):938-941.

[4] 李平.永磁同步电机的建模与参数辨识[J].计算机仿真,2011,28(08):401-404.

[5] 何杰,王家军.基于SVPWM的永磁同步电动机系统建模与仿真[J].机电工程,2009,26(07):77-82.

[6] 张红生,吴炳娇.永磁同步电机电机本体数学模型在MATLAB下的仿真[J].自动化与仪器仪表,2012,(02):134-135+138.

[7] 陈俊硕,刘景林,张颖. 永磁同步电机优化控制系统建模与仿真[J]. 计算机仿真,2013,30(08):341-345.

[8] 袁登科,陶生桂.交流永磁电机变频调速系统[M].北京:机械工业出版社,2011.

[9] 刘金海.Simulink自带永磁同步电动机模型矢量坐标变换分析与国产化改造[J].漳州师范学院学报:自然科学版，2010，23(4)4:73-76

[10] 王莉娜,杨宗军.SIMULINK中PMSM模型的改进及在参数辨识中的应用[J].电机与控制学报,2012(7):77-82.

[11] 王松.永磁同步电机的参数辨识及控制策略研究[D].北京：北京交通大学,2011.

[12] Seung-Ki S.电机传动系统控制[M].北京：机械工业出版社，2013.

TheThreePhaseCoordinateSystemModelingofPermanentMagneticSynchronousMotorBasedonMatlab

CHEN Wen-zhuo，JIN Wen-tao

(SchoolofElectronicandInformationEngineering,NorthChinaInstitueofScienceandTechnology，Yanjiao，065201，China)

The present models of Permanent Magnetic Synchronous Motor(PMSM) have shortcomings. On the one hand, the PMSM model in MatlabSimulink applies the coordinate system which is quite different from those recorded in the reference materials in China, and because of its highly integrity, it is hard to modify the parameters and structure. And on the other hand, custom models are often built according to Clarke transformation, which have two phase inputs, while in engineering application the motor uses three phase input. So this paper combines the three phase stator equation with the Clarke transformation matrix, and simplifies the flux linkage by analyzing the relationship between the direct axis inductance and quadrature axis inductance,to derive the three phase coordinate system model with both motor equation and electromagnetic torque equation. It is proved by the simulation result that the new model here is correct and effective.

PMSM；Three phase coordinate system；Matlab；Modeling

2017-04-05

河北省高等学校科学技术研究项目(ZC2016072)；中央高校基本科研业务费资助项目(3142015101、3142014074)

陈文卓(1985-)，女，河南南阳人，硕士，华北科技学院电子信息工程学院讲师，主要从事电机控制技术及建模方面的研究.E-mail:wenzhuochen@sohu.com

TM351

A

1672-7169(2017)04-0052-05