火积损失极值原理在热源塔热泵系统优化运行中的应用
林涛,梁彩华,郜骅,2,张小松
火积损失极值原理在热源塔热泵系统优化运行中的应用
林涛1,梁彩华1,郜骅1,2,张小松1
(1. 东南大学能源与环境学院,江苏南京,210096;2. 浙江省建筑设计研究院,浙江杭州,310006)
为优化热源塔热泵系统的运行,基于火积理论,提出热源塔热泵系统火积损失极值原理,并构建热源塔热泵系统火积损失模型。通过模拟和实验分别研究在定系统供热量和定系统输入功率时,系统在不同运行工况下的火积损失率,得出系统的最优运行工况。研究结果表明:系统火积损失率实验值与模拟值的相对误差不超过9.8%,表明系统火积损失模型具有较高的精度;当系统供热量为4 kW时,最优运行工况为压缩机频率51 Hz,热水流量0.5 kg/s,溶液流量0.6 kg/s,风量1.4 kg/s,此时系统火积损失率最大,系统输入功率最小,系统效率最高;当系统输入功率为2 kW时,最优运行工况为压缩机频率72 Hz,热水流量0.4 kg/s,溶液流量0.5 kg/s,风量1.6 kg/s,系统火积损失率最小,系统供热量最大,系统效率最高。
热源塔热泵;优化运行;火积损失极值原理;火积损失模型;模拟与实验;系统效率
在夏热冬冷地区,热源塔热泵作为一种新型的热泵装置,兼顾高效制冷与制热的同时能够有效避免空气源热泵冬季结霜问题,正受到越来越广泛的关注。目前对热源塔热泵的研究主要集中在3个方面:1) 热源塔传热传质及凝水性研究[1−3];2) 空气、溶液及塔参数对热源塔取热量和热泵系统性能的影响规律[4−5];3) 热源塔溶液物性以及溶液再生研究[6−8]。上述研究重点关注于热源塔热泵系统的适用性和性能研究,而对热源塔热泵系统优化运行的研究较少。传统热泵系统优化的研究方法主要有能效分析法和火用分析法,但能效分析法只考虑了能量守恒转化定律,重点在于“量”,却忽略了能量转化过程中的“质”[9];火用分析法主要用于热功转换过程的研究,而热泵系统不仅包括热功转换过程,也包含搬运和输送热量的过程,导致火用分析法在热泵系统应用存在一定的局限性。基于导热与导电的对比,GUO等[10]提出了用以表征热量传递能力的新概念——火积。研究表明:传热过程必然伴随着火积的损耗,即存在火积耗散。基于火积耗散的概念,火积耗散极值原理、最小热阻原理等得以发展并被应用于热传导、热对流、热辐射、换热器、热网络等多种传热过程的优化与分析中[11]。CHENG等[12−14]提出了火积损失的概念,对于闭口热力学系统而言, 火积损失为流入和流出系统的火积流之差, 也等于火积耗散和功火积之和,建立了火积损失与系统输出功之间的对应关系, 并将火积损失应用于Brayton循环等的分析和优化中。ACIKKALP[15−16]利用火积理论研究了卡诺循环、制冷循环中各热力学参数间的关系,表明了火积在热力学循环中应用的可行性。相比能效分析法,火积分析法充分考虑了热量在不同温度状态下的“势”;相比火用分析法,火积分析法在热功转换过程和热量传递过程中都有很好的应用。XU等[17]基于火积理论,对蒸汽压缩式制冷系统进行了包含运行参数和结构参数的全局优化研究,但XU等[17]只是将 火积作为一个中间变量,推导出运行参数和结构参数的关系,进而利用拉格朗日乘数法进行优化,并没有直接将火积作为系统的性能参数应用到优化中。本文作者将火积理论应用到热源塔热泵系统热力循环中,提出热源塔热泵系统火积损失极值原理,并构建了热源塔热泵系统的火积损失模型。通过模拟与实验研究对比,探索在定系统供热量和定系统输入功率条件下,热源塔热泵系统火积损失极值原理在热源塔热泵系统优化运行中的应用,为热源塔热泵系统的优化运行提供了新思路。
1 热泵系统火积损失极值原理
热源塔热泵系统中,能量平衡方程有

图1 热源塔热泵系统能量转换
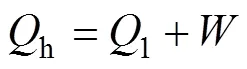
其中:

式中:h和l分别为工质与高,低温热源之间的换热量,kW;,c,a,s和h分别为系统输入功率、压缩机功率、风机功率、溶液泵功率和热水泵功率,kW。
热源塔热泵系统火积损失包含2个部分,分别是工质与高低温热源传热引起的火积损失和工质在热力学循环中做功引起的火积损失。
工质与低温和高温热源传热引起的火积损失率[10]分别为:
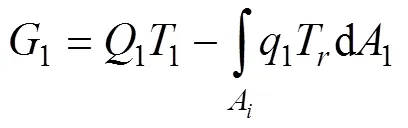

式中:l和h分别为低、高温热源温度,K;l和h分别为工质与低、高温热源的热通量,kW/m2;l和h分别为工质与低、高温热源的换热面积,m2。
对工质,有热力学第一定律

方程两边同乘工质温度r

对于热力学循环有

工质在热力学循环中内能不变,所以

式中:Q和W分别为工质在热力学循环中传热引起的火积损失率和做功引起的火积损失率,kW·K。
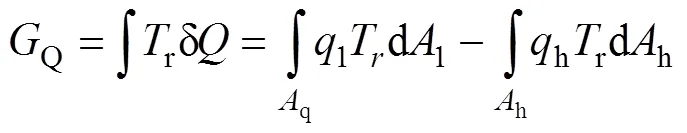
所以,

热源塔热泵系统的火积损失率为工质与高低温热源传热引起的火积损失率和工质在热力学循环中做功引起的火积损失率之和,结合式(3),(4)和(10)可得
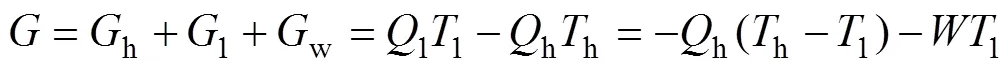
因为h,l和都为正值,且h大于l,所以系统火积损失率始终为负值,即系统火积不是减少,而是增加的。由式(11)可知:给定高低温热源温度时,当系统供热量一定,系统火积损失率最大时,系统输入功率最小,系统效率最高;当系统输入功率一定,系统 火积损失率最小时,系统供热量最大,系统效率最高,这就是热源塔热泵系统火积损失极值原理。
2 热源塔热泵系统火积损失模型
热源塔热泵系统包括热泵机组、热源塔及管道。本文将分别构建压缩机、冷凝器、蒸发器、热源塔、溶液泵、热水泵、风机及管道的火积损失模型,最后形成整个热源塔热泵系统的火积损失模型。
在构建热源塔热泵系统火积损失模型过程中,进行以下假设:
1) 压缩机的压缩过程绝热;
2)驶制冷剂在热力膨胀阀前后的焓值不变。
2.1 压缩机模型
压缩机是一个开口热力学系,采用开口热力学的火积平衡方程对其进行分析,压缩机的输入功用来增加制冷剂的火积,压缩机过程火积损失率为

式中:r为制冷剂质量流量,kg/s;1和2分别为压缩机吸气焓和排气焓,kJ/kg;ci和co分别为是压缩机的吸排气温度,K。
2.2 冷凝器模型
图2所示为冷凝器工作过程。冷凝器的传热过程分为3段:过热段、冷凝段和过冷段。在冷凝器中,存在由传热引起的火积损失。
冷凝器中由于传热引起的火积损失率为


式中:c1,c2和c3分别为过热段、冷凝段和过冷段的换热量,kW。
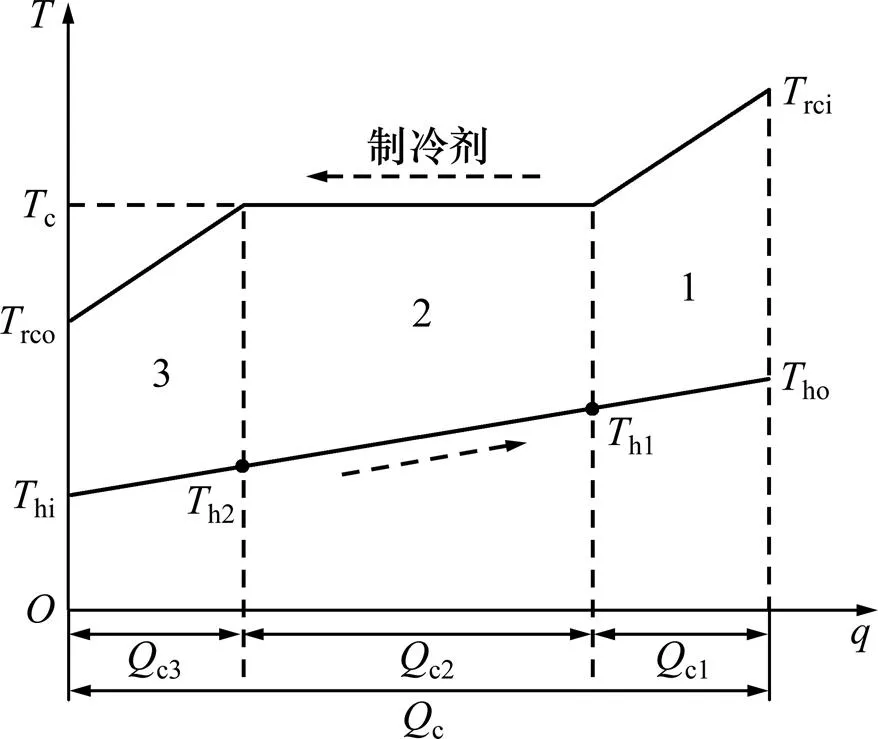
图2 冷凝器传热过程的T−q
2.3 蒸发器模型
图3所示为蒸发器工作过程。蒸发器的传热过程分为2段:蒸发段和过热段。与冷凝器一样,蒸发器中同样存在由传热引起的火积损失。
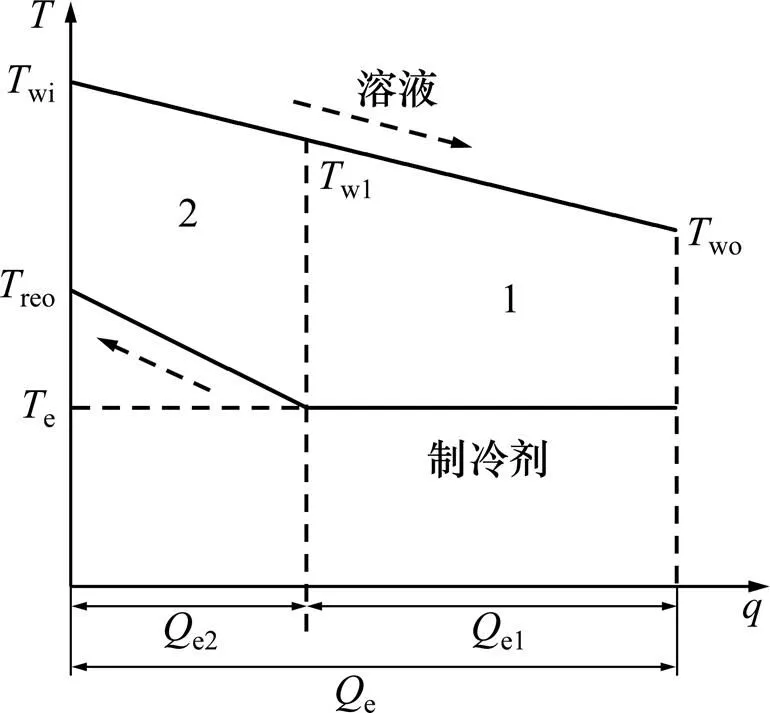
图3 蒸发器传热过程的T−q
蒸发器中由传热引起的火积损失率为

式中:e1和e2分别为蒸发段和过热段的换热量,kW。
2.4 热源塔模型
在热源塔中,空气与溶液进行热质交换,空气一方面以显热的形式与溶液进行换热,另一方面,由于空气中的水蒸气分压力和溶液表面水蒸气分压力的关系,会有水蒸气的凝结过程,引起潜热交换。
由于空气和溶液之间显热交换引起的显热火积损失率为
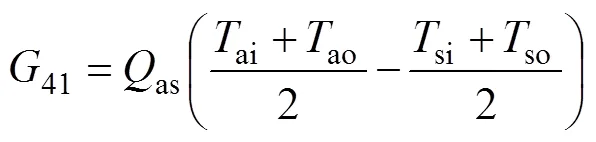
式中:as为空气与溶液的显热换热量,kW;ai和ao分别为空气进、出塔温度,K;si和so分别为溶液进、出塔温度,K。
由于空气和溶液之间潜热交换引起的湿火积损失率为

式中:a为空气质量流量,kg/s;i和o分别为空气进出塔绝对含湿量,g/kg。
将湿火积损失率转换为显热火积损失率[18]

式中:0为水蒸气的汽化潜热,kJ/kg;l为进塔空气对应的露点温度,K。
综上,热源塔火积损失率为
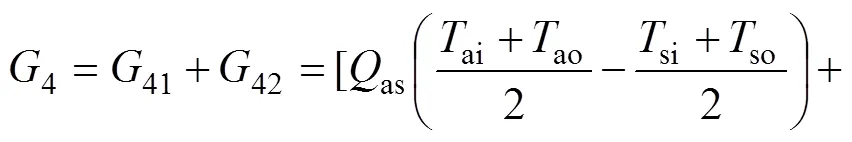

2.5 风机、溶液泵和热水泵模型
风机、溶液泵和热水泵都是流体的输送设备,其输入功用于克服流体的黏性阻力耗散,做功导致流体的火积增加。它们的火积损失率分别为:
5=−aia(19)
6=−sis(20)
7=−hih(21)
式中:hi为冷凝器进口热水温度,K。
2.6 管道模型
设流体在管道中的流动是由入口和出口之间的有限压差引起的,且流体的流动为稳态绝热,那么流体在管道上的火积损失是由流体在管道上的流动阻力引起的黏性耗散[19],即
d+d/=0 (22)
方程两边同乘以,有
d=d/=0 (23)
因而流体阻力引起的热力学火积损失率为
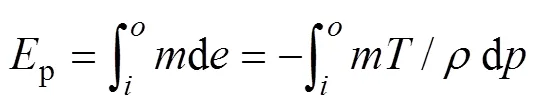
管道主要包含热源塔风道、溶液管道和热水管道。
热源塔中空气为理想气体,风道中由空气阻力引起的火积损失率[18]为

式中:为理想气体常数,kJ/(kmol·K);ai和ao分别为空气进、出塔压力,kPa。
溶液和热水都是不可压缩流体,由流动阻力引起的火积损失率分别为:

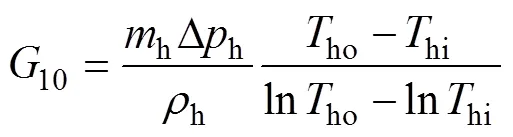
式中:s和h分别为溶液和热水流量,kg/s;Δs和Δh分别为溶液管路和热水管路压差,kPa;s和h分别为溶液和热水密度,kg/m3;ho为冷凝器出口热水温度,K。
综上,热源塔热泵系统火积损失率为
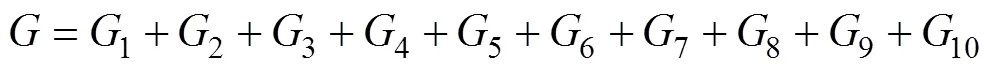
式(28)为热源塔热泵系统火积损失率方程,下面将用此方程对模拟和实验机组运行过程中的热源塔热泵系统火积损失率进行计算。
3 模拟与实验结果分析
3.1 模拟仿真软件
模拟热泵机组运行过程采用VB模拟仿真软件,热源塔热泵系统的各个部件运行是一个相互耦合的工作循环,其程序的实现方式如图4所示。
3.2 实验装置
热源塔热泵实验台系统图如图5所示。压缩机采用涡旋压缩机,频率变化范围为30~110 Hz,功率为1.6 kW(70 Hz),排气量为23.2 mL/min,制冷剂为R22。冷凝器和蒸发器均采用板式换热器,其中冷凝器换热面积为0.76 m2,蒸发器换热面积为1.26 m2。节流阀采用热力膨胀阀,热源塔采用开式热源塔,工作介质为乙二醇溶液。压力传感器测量范围有0~1.5 MPa和0~2.5 MPa 2种规格,测量精度为±0.5%。流量传感器采用涡轮流量传感器,测量精度为1.0%。进出口空气温度和相对湿度采用温湿度传感仪测量,温度误差在0.1 ℃以内,相对湿度的误差在1%以内。风速测量采用手持热线式风速仪,风速测量精度为0.05 m/s。压缩机功率测量采用三相电参数综合测量仪,测量精度为±0.5%,测量系统所有信号采用数据采集仪采集并通过电脑上实时显示、保存和分析。压缩机、热水泵、溶液泵和风机均可通过变频器调节。实验装置可实现冷凝器进出口热水温度、蒸发器进出口溶液温度、热源塔进出口溶液温度、环境温湿度、压缩机吸排气压力、溶液流量、热水流量、风量以及压缩机功率等参数的实时测量。

图4 程序实现方式流程图

图5 热源塔热泵系统图
3.3 模拟与实验结果对比
3.3.1 定系统供热量条件下系统火积损失率分析
室外气温为2℃,相对温度为70%,热源塔溶液为20%(质量分数)的乙二醇溶液。通过调节压缩机,热水泵,溶液泵和风机的频率,使得热泵系统的供热量为4 kW,符合系统供热量4 kW的运行工况参数如表1所示。其中,为压缩机频率。

表1 定系统供热量4 kW模拟和实验运行工况
图6所示为热源塔热泵系统火积损失率和系统输入功率在定系统供热量4 kW时,不同运行工况的模拟和实验值。由图6可知:系统火积损失率实验值和模拟值相对误差不超过8.8%,系统输入功率实验值和模拟值相对误差不超过9.9%,表明热源塔热泵系统火积损失模型具有较高的精度。系统火积损失率和输入功率呈现相反的变化规律,当系统火积损失率越大时,系统输入功率越小,系统效率越高,很好地验证了热源塔热泵系统火积损失极值原理。在运行工况3,即压缩机频率为51 Hz,热水流量为0.5 kg/s,溶液流量为0.6 kg/s,风量为1.4 kg/s时,系统火积损失率最大,对应的系统总功率最小,系统效率最高,此工况为定系统供热量为4 kW时的最优运行工况。
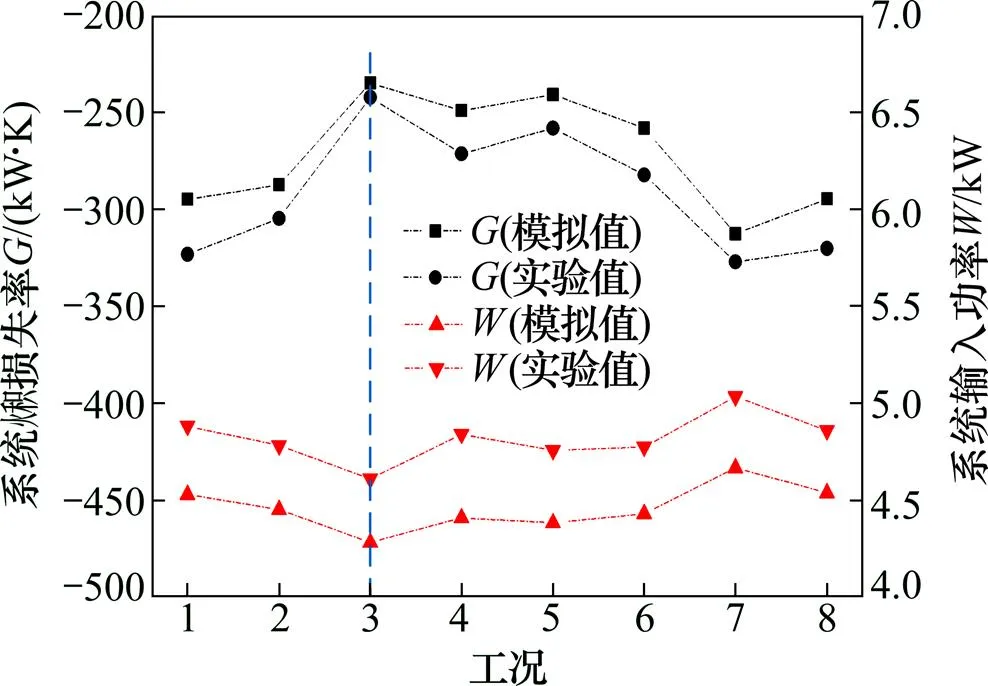
图6 定系统供热量4 kW系统火积损失率和输入功率
3.3.2 定系统输入功率条件下系统火积损失率分析
当室外温度为2 ℃,相对湿度为70%,热源塔溶液为20%(质量分数)的乙二醇溶液时,通过调节压缩机、热水泵、溶液泵和风机的频率,使得系统输入功率为2 kW。符合系统输入功率2 kW的运行工况参数如表2所示。
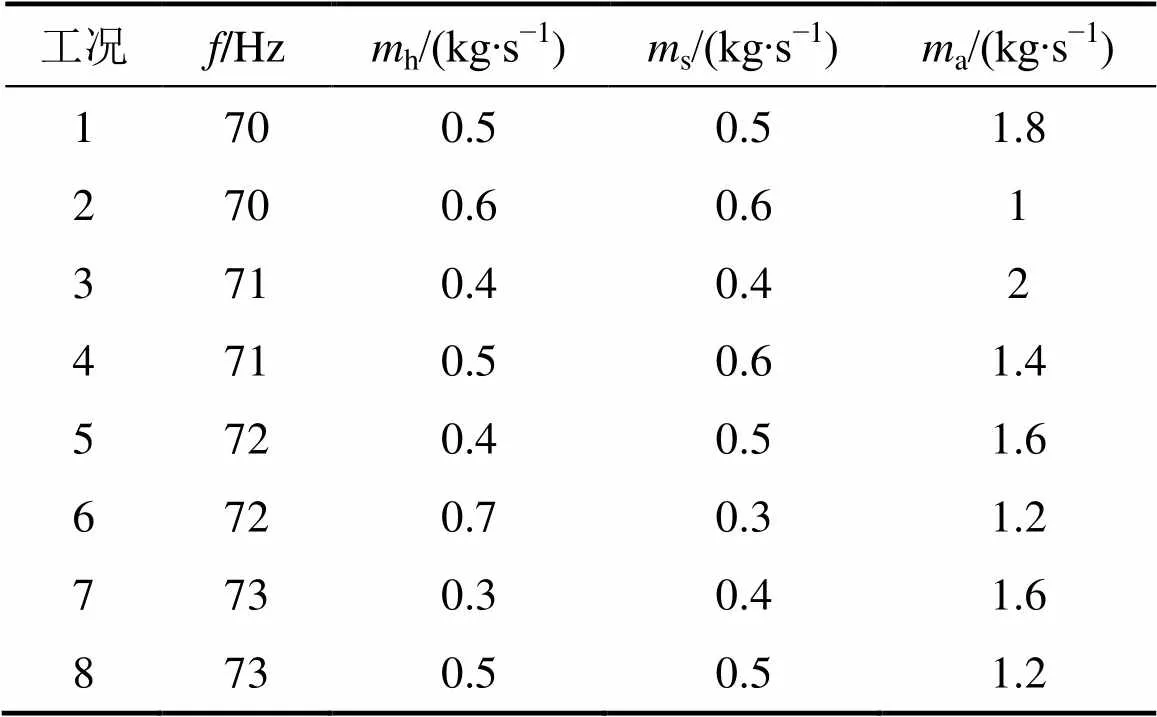
表2 定系统输入功率2 kW模拟和实验运行工况
图7所示为热源塔热泵系统火积损失率和供热量在定系统输入功率2 kW时,不同运行工况的模拟和实验值。由图7可知:系统火积损失率实验值和模拟值相对误差不超过9.8%,供热量实验值和模拟值相对误差不超过7.9%,表明实验值与模拟值具有较好的一致性。系统火积损失率和供热量呈现相反的变化规律,当系统火积损失率越小时,系统供热量越大,系统效率越高,很好地验证了热源塔热泵系统火积损失极值原理。在运行工况5,即压缩机频率为72 Hz,热水流量为0.4 kg/s,溶液流量为0.5 kg/s,风量为1.6 kg/s时,系统火积损失率最小,对应的系统供热量最大,系统效率最高,此工况为定系统输入功率2 kW时的最优运行工况。
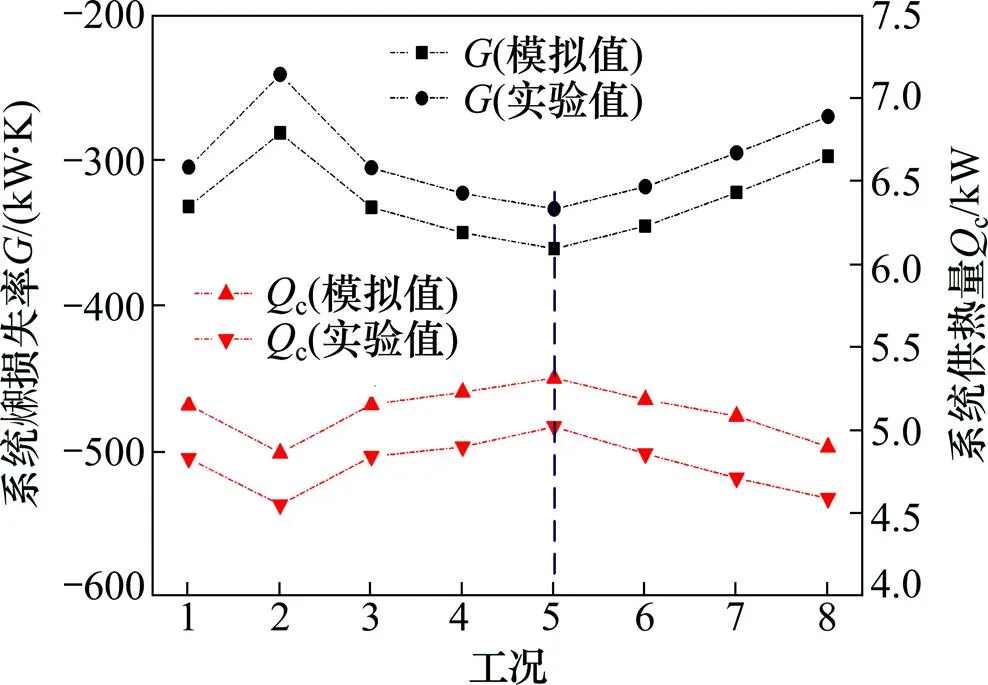
图7 定系统输入功率2 kW系统火积损失率和供热量
4 结论
1) 基于火积理论,提出了热源塔热泵系统火积损失极值原理,即给定高低温热源的温度时,当系统供热量一定,系统火积损失率最大对应的系统输入功率最小,系统效率最高;当系统输入功率一定,系统火积损失率最小时对应的系统供热量最大,系统效率最高。
2) 分别构建了热源塔热泵系统压缩机、冷凝器、蒸发器、热源塔、溶液泵、热水泵、风机和管道的火积损失模型,得到了系统火积损失率的计算公式。
3) 系统火积损失率实验值和模拟值相对偏差不超过9.8%,表明热源塔热泵系统火积损失模型具有较高的精度。当系统供热量为4 kW时,最优运行工况为压缩机频率51 Hz,热水流量0.5 kg/s,溶液流量0.6 kg/s,风量1.4 kg/s;当系统输入功率为2 kW时,最优运行工况为压缩机频率72 Hz,热水流量0.4 kg/s,溶液流量0.5 kg/s,风量1.6 kg/s。
[1] 文先太, 梁彩华, 张小松, 等. 热源塔传质特性的分析和实验研究[J]. 化工学报, 2011, 62(4): 901−907. WEN Xiantai, LIANG Caihua, ZHANG Xiaosong, et al. Mass transfer characteristics in heat-source tower[J]. CIESC Journal, 2011, 62(4): 901−907.
[2] WEN X, LIANG C, ZHANG X. Experimental study on heat transfer coefficient between air and liquid in the cross-flow heat-source tower[J]. Building and Environment, 2012, 57(11): 205−213.
[3] 文先太, 梁彩华, 刘成兴, 等. 叉流热源塔传热传质模型的建立及实验验证 [J]. 化工学报, 2012, 63(8): 2398−2404. WEN Xiantai, LIANG Caihua, LIU Chengxing, et al. Verification of model for heat and mass transfer process in cross flow heat-source tower[J]. CIESC Journal, 2012, 63(8): 2398−2404.
[4] LUO Yi, MA Rongsheng, DING Xingfeng, et al. A study of the mechanical draft heating/cooling tower heat pump system[C]//6th International Symposium on Heating, Ventilating and Air Conditioning. 2009: 702−707.
[5] LI Nianping, ZHANG Wenjie, WANG Lijie, et al. Experimental study on energy efficiency of heat-source tower heat pump units in winter condition[C]//Third International Conference on Measuring Technology and Mechatronics Automation. New York, USA: IEEE, 2011: 135−138.
[6] DIAZ G. Numerical investigation of transient heat and mass transfer in a parallel-flow liquid-desiccant absorber[J]. Heat and Mass Transfer, 2010, 46(11/12): 1335−1344.
[7] RATTNER A S, NAGAVARAPU A K, GARIMELLA S, et al. Modeling of a flat plate membrane-distillation system for liquid desiccant regeneration in air-conditioning applications[J]. International Journal of Heat and Mass Transfer, 2011, 54(15): 3650−3660.
[8] LIU X H, JIANG Y, CHANG X M, et al. Experimental investigation of the heat and mass transfer between air and liquid desiccant in a cross-flow regenerator[J]. Renewable Energy, 2007, 32(10): 1623−1636.
[9] BACCOLI R, MASTINO C, RODRIGUEZ G. Energy and exergy analysis of a geothermal heat pump air conditioning system[J]. Applied Thermal Engineering, 2015, 86: 333−347.
[10] GUO Zengyuan, ZHU Hongye, LIANG Xingang. Entransy: A physical quantity deseribing heat transfer ability[J]. International Journal of Heat and Mass Transfer, 2007, 50(13): 2545−2556.
[11] CHEN Qun, XU Yunchao, GUO Zengyuan. The property diagram in heat transfer and its applications[J]. Chinese Sci Bull, 2012, 57(35): 4646−4652.
[12] CHENG Xuetao, LIANG Xingang. Entransy loss in thermodynamic processes and its application[J]. Energy, 2012, 44: 964−972.
[13] CHENG Xuetao, WANG Wenhua, LIANG Xingang. Optimization of heat transfer and heat-work conversion based on generalized heat transfer law[J]. Sci China Tech Sci, 2012, 55(10): 2847−2855.
[14] CHENG Xuetao, WANG Wenhua, LIANG Xingang. Entransy analysis of open thermodynamics systems[J]. Chin Sci Bull, 2012, 57(22): 2934−2940.
[15] ACIKKALP E. Entransy analysis of irreversible Carnot-like heat engine and refrigeration cycles and the relationships among various thermodynamic parameters[J]. Energy Conversion and Management, 2014, 80: 535−542.
[16] ACIKKALP E. Entransy analysis of irreversible heat pump using Newton and Dulong-Petit heat transfer laws and relations with its performance[J]. Energy Conversion and Management, 2014, 86: 792−800.
[17] XU Yunchao, CHEN Qun. A theoretical global optimization method for vapor-compression refrigeration systems based on entransy theory[J]. Energy, 2013, 60(9): 464−473.
[18] 谢晓云, 江亿. 蒸发冷却制备冷水流程的热学分析[J]. 暖通空调, 2011, 41(3): 65−76. XIE Xiaoyun, JIANG Yi. Thermological analysis of chilled water by evaporative cooling processes[J]. Heating, Ventilating and Air Conditioning, 2011, 41(3): 65−76.
[19] 许明田, 程林, 郭江峰. 火积耗散理论在换热器设计中的应用[J]. 工程热物理学报, 2009, 30(9): 2090−2092. XU Mingtian, CHENG Lin, GUO Jiangfeng. An application of entransy dissipation theory to heat exchanger design[J]. Journal of Engineering Thermophysics, 2009, 30(12): 2090−2092.
(编辑 杨幼平)
Application of extremum entransy loss principle in optimization operation of heat source tower heat pump system
LIN Tao1, LIANG Caihua1, GAO Hua1, 2, ZHANG Xiaosong1
(1. College of Energy and Environment, Southeast University, Nanjing 210096, China;2. Zhejiang Province Institute of Architectural Design and Research, Hangzhou 310006, China)
To optimize the operation of heat source tower heat pump, extremum entransy loss principle was proposed and entransy loss model was established for heat source tower heat pump system based on entransy theory. The system entransy loss rate was studied under different operation conditions for system heat load fixed or input power consumption fixed by means of simulation and experiment so as to get the optimization operation conditions. The results show that relative error of entransy loss rate values between simulation and experiment is less than 9.8% which proves that the model is adequately accurate. When system heat load is 4 kW, the optimization operation condition parameters are 51 Hz for compressor frequency, 0.5 kg/s for hot water flow rate, 0.6 kg/s for solution flow rate and 1.4 kg/s for air flow rate, which leads to the maximum system entransy loss rate, minimum system input power consumption and maximum system efficiency. When system input power consumption is 2 kW, the optimization operation condition parameters are 72 Hz for compressor frequency, 0.4 kg/s for hot water flow rate, 0.5 kg/s for solution flow rate and 1.6kg/s for air flow rate, which leads to the minimum system entransy loss rate, maximum system heat load and maximum system efficiency.
heat source tower heat pump; optimization operation; extremum entransy loss principle; entransy loss model; simulation and experiment; system efficiency
10.11817/j.issn.1672−7207.2017.10.036
TK124
A
1672−7207(2017)10−2823−07
2016−10−22;
修回日期:2017−01−14
国家自然科学基金资助项目(51106023)(Project (51106023) supported by the National Natural Science Foundation of China)
梁彩华,博士,研究员,从事制冷空调热泵系统控制、节能与系统优化等研究;E-mail:caihualiang@163.com

