干堆排尾对露天坑坑下采场稳定性的影响
陈佳耀,史秀志,周健,邱贤阳,王洋
干堆排尾对露天坑坑下采场稳定性的影响
陈佳耀,史秀志,周健,邱贤阳,王洋
(中南大学资源与安全工程学院,湖南长沙,410083)
针对铜绿山露天转地下矿山利用露天坑干堆尾砂技术,采用FLAC3D数值软件,运用强度折减法及拟合函数位移突变特征法,对露天坑尾砂堆积过程进行破坏判定及稳定性安全系数求解,从而分析露天坑排尾的可行性。研究结果表明:当尾砂堆高=0 m时,最优境界顶柱高度=20 m,可允许的采场跨度>34 m,主要破坏形式是空区顶板两端剪切破坏;当>0 m和>30 m时,采场有垮塌现象,露天坑台阶塑性区明显;当>160 m时,空区塑性区面积及顶板位移迅速增大,堆积对空区的破坏程度大为增加,采场的合理跨度进一步减小。
露天坑堆尾;境界顶柱;地下采场稳定性;动态监测;数值模拟
目前,国内露天矿山在转地下开采的过程中都面临着一些困难,主要包括尾砂库剩余容积不足、境界顶柱对地下采矿的安全稳定性、采场回采本身的安全性等。这些问题随着地下开采深度的延伸会更加的尖锐,若不加以克服将会对生产的连续性以及矿山的经济效益造成巨大的损失。尾矿压滤干堆是近年来提出的经济环保、切实可行的新技术,它对于工业用水的循环利用和地下水的保护有很好的作用,排放尾砂的预脱水使得露天坑排放尾砂成为可能。国内外很多专家学者在这方面取得了重要的研究成果,王新民等[1]利用模糊数学和层次分析法对露天转地下的最佳开采模式进行研究;李地元等[2]采用结构力学梁理论及K.B.鲁佩涅依特理论估算法,并结合数值模拟程序分析了采空区顶板与采空区跨度之间的对应关系;张亚宾[3]利用有限元进行露天采空区排尾对地下开采影响的研究;夏世友[4]利用FLAC3D数值模拟研究了露天坑回填对地下岩体的应力应变场的影响。然而,现阶段在关注露天坑合理化利用的同时,研究上部尾砂的堆积对于境界顶柱及地下采场参数合理化的案例较少。据统计,露天矿转地下开采的过程中,由于错误预估境界顶柱的厚度而造成的经济损失数目巨大,实现参数最优化对于生产效益的提高和经济的可持续发展意义重大。本文作者就铜绿山矿Ⅰ号矿体露天铜铁矿转地下开采的实际情况,建立数值模型,考虑不同回填高度下不同参数的开挖模拟,确定空区破坏形式及具体特征;对于不破坏的空区进行塑性区面积计算,最终确定合理顶柱及跨度,并分析尾砂堆积与空区变形的关系,为后续的生产施工提供理论和技术指导。
1 工程概况
铜绿山露天矿目前共形成20万m2露采坑面积,为合理利用采坑空间,保护周边居民生活工作环境,拟规划采用尾砂干堆技术进行尾砂堆放,对露天坑底部位置进行全尾砂胶结充填以进行高效的地下开采作业。矿体主要呈似层、透镜状,为使模拟具有代表性,选取12号勘探线处进行深入研究,该线地质复杂且处中间重要位置。如图1所示,Ⅰ号矿体大部分赋存于−305~185 m,平均厚度为80 m,倾角为60° ~ 80°,南北走向,沿走向布置的长度为150 m。矿体上下盘底围岩主要包括大理岩、斜长石岩、矽卡岩,且有断层贯穿于露天坑岩石之间,易发生渗透、导水等现象。斜长石岩不稳固且蚀变较弱,大理岩为中等稳固,整个露天矿的岩性较复杂,对模拟带来了较大的困难。其中图1模拟了回填土回填后露天坑的情况,坑口距离坑底的垂直距离为,并假设境界顶柱高度为,采场空区跨度为。

图1 12 号勘探线剖面示意图
由于地质结构复杂,各类参数涉及的岩体类别多,故为了简化研究,获取代表性的岩体料力学参数如表 1 所示。
2 数值模拟与计算分析
2.1 数值计算模型思路
根据提供的材料参数及赋存条件,建立相关模型,利用模型进行尾砂堆积以及采场开挖的模拟。开挖之前通过FLAC3D的elastic命令,获取较为准确的初始应力场。进行相应空区的开挖命令,通过调整境界顶柱的高度和采场跨度2个主要因素,结合判据,确定合理的最优值。进行堆积尾砂的模拟,以 10 m为单位进行堆加,观察合理塑性区以及关键点的位移情况。研究流程见图 2。
本文通过监测重要点的相关位移以及重要位置的塑性区进行判断,主要内容如下:监测系统最大不平衡力(hist unbalance force),根据其收敛性进行判断,收敛仅说明系统处于平衡状态,不能判定破坏,收敛是观察系统的重要前提;另外,应通过结合观察关键点(重要位置点)的位移和应力进一步确定,统计塑性区贯通面积也是重要的指标之一。

表1 岩体物理力学参数

图2 研究流程图
2.2 数值建立及监测点布置
本模型采用 1:1 比例建立,整个模型包括节点 10 420个,单元5 091个,长为480 m,宽为4 m,高为338 m。模型的初始尾砂堆高为 0 m,模拟过程进行逐层尾砂堆积,如图3所示。
采场采用上向水平分层充填法进行回采,为保证安全,结合使用3 m,“两采一充”方式高效回收矿石。保证最大的裸露高度少于6 m,及时支护不稳固顶板及边帮。故采空区的高度为6 m,每隔3 m向上推进,模拟预留最大的境界顶柱高度为 35m,最小高度为 8 m,共 11组。采场的跨度采用 4 m为单位作为间隔,最小跨度10 m,最大34 m,共7组。
本文的模拟总体分2步:1) 首先针对无尾砂堆积时,不同采场参数和高度进行地下开采(null),如图3所示,设置监测点1号、2号和3号,其中1号监测点位于采空区中心位置(顶板中心位置),通常该位置易发生受拉破坏;2号和3号位于采场的转角处,通常容易发生剪切破坏。分别监测 1号、2号和3号的竖直位移、水平应力、塑性区特征和面积以及到达平衡状态的时步,利用history命令记录,history write功能输出具体数值[5−8]。2) 进行排尾砂模拟,分别对露天坑台阶面的顶点位置进行检测,该位置容易发生应力集中现象,主要包括 4号和5号监测点。另外,对露天坑底部 6号和7号监测点、矿体边界8号监测点分别监测与统计,利用history write导入MATLAB软件统计。
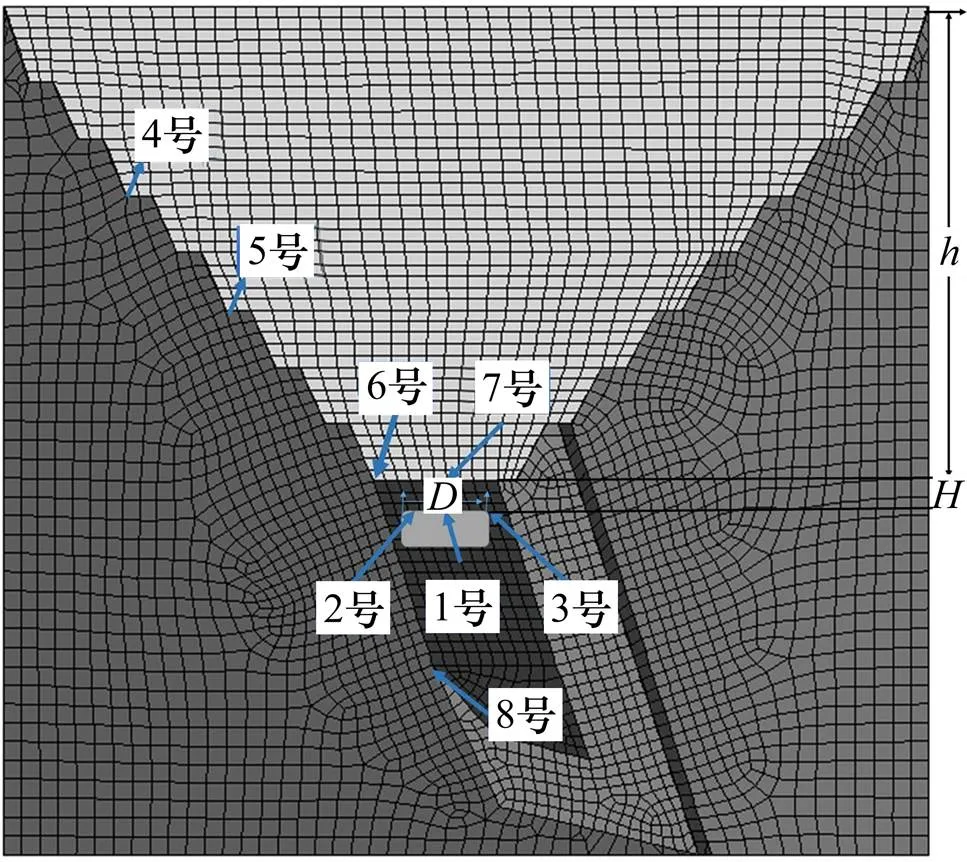
图3 矿体开挖模拟的FLAC3D模型及监测点布置
3 模拟结果统计与分析
DUNCAN[9]指出斜坡的稳定性系数可以定义为使斜坡刚好达到临界破坏状态时对土的剪切强度进行折减的程度。毕肖普将稳定性系数定义为整个滑裂面上平均抗剪强度与实际产生的平均剪应力之比。因此,在FLAC3D模拟过程中,可以在达到临界平衡或临界破坏状态的前提下,定义一个折减系数为实际抗剪强度与折减抗剪强度的比值F,实现了判定依据的添加和完善[10−12]。本文利用FLAC3D自带Fish语言编程定义了折减系数,通过对内聚力、内摩擦角、抗剪强度3个参数进行折减,通过折减强度理论对系统进行运算,设置力不平衡率=5×10−6。
3.1 未填尾砂(h=0 m)和境界顶柱H不同时开挖模拟
模拟第一步即在无尾砂堆积情况下进行地下开挖,模拟境界顶柱的最大高度预留 35 m,并对该高度实现 3 m梯度递减,最小高度为 8 m。
3.1.1 位移分析
当境界顶柱为 8~17 m时,根据监测点 1号、2号和3号的垂直位移绘制曲线图,如图 4 所示。
通过数值模拟发现当为8,11和14 m时均有发生破坏现象。从图4可见:图4(a)~(c)都有突变特征,只能定性判断破坏点的存在。在境界顶柱破坏高度未确定时,选择下一步模拟高度是不合理的。
根据曲线的突变特征[12],假设监测点位移与采场跨度之间满足泰勒级数曲线的形式,选择拟合曲线方程的形式如下:
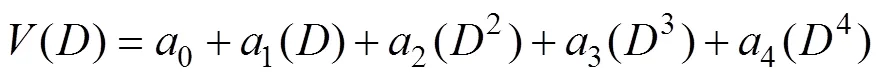
式中:0,1,2,3和4为该多项式待定系数;为采场跨度;为采场顶板中心位移。
/m:(a) 8;(b) 11;(c) 14;(d) 17
1—3号监测点;2—2号监测点;3—1号监测点。
图4 不同境界顶柱厚度下监测点的位移
Fig. 4 Displacement of monitoring points under different thicknesses
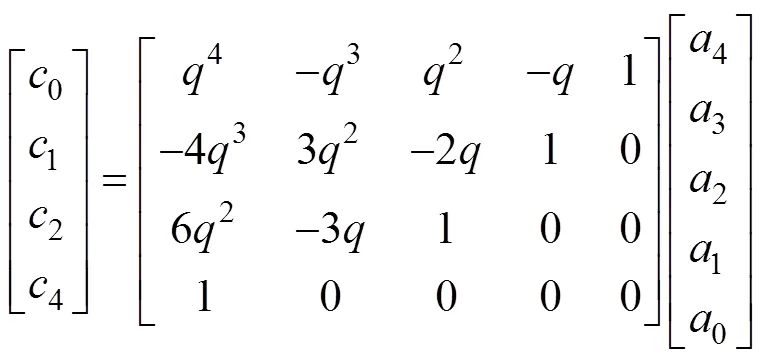
简化得


忽略项的式(3)为尖点突变模式势函数的标准表达式。式(3)为采场顶板的稳定模型,其判别式为
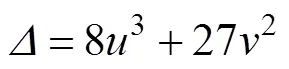
=0为临界状态,其实满足如下叉集方程:
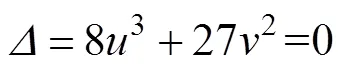
可进一步得到尖点突变模型的破坏判据如下:当<0时,采场处于临界失稳状态;当=0时,采场处于临界失稳状态;当>0时,采场处于临界失稳状态;而=0所对应的值即为“突变点”。
从图 4 可以看出:采场顶板和两侧的垂直位移都随着跨度的变大而增大,且和境界顶柱的高度没有直接关系。在同一境界顶柱高度下,顶板的垂直位移比两侧监测点的位移更大,且各监测点位移变化的速率在突变前后均有较大的变化。从表2可以看出:当为8,11和14 m时,均存在临界失稳状态=0,当=8 m时,跨度=21.196 m的采场临界破坏;当=11 m时,跨度=24.104 m采场临界破坏,当=14 m时,跨度=32.641 m采场临界破坏,此时的突变跨度在工程实践中一般取整,而当=17 m时在跨度34 m内未发生临界破坏,全过程≠0。从图4可知:在发生临界破坏前,监测点存在位移变化速率突变点,在突变位置之前,采场顶板受拉明显且实现应力释放,采场没有发生破坏;突变位置之后,顶板位移明显增大,可能有垮塌的危险,故可以把速率突变点定性的看成临界破坏的“前点”,而“前点”和临界=0对应的点之间均有破坏危险,由图4可见:=8 m的“前点”=20 m,=11 m的“前点”=29 m,=14 m的“前点”=32 m,两者之间差距较小,可以用速率突变点预估破坏临界点。
从图 5 可以看出:当采场发生垮塌时,顶板向空区大面积下沉,此时 1号、2号和3号关键监测点的位移是一个不断增大的过程,且位移的增大速率大。由于=8,11和14 m时均存在空区跨度较大便破坏的记录,下文的模拟将不考虑作为后期堆积尾砂试验的参数,即采场空区稳定性的分析将从境界顶柱= 14 m开始模拟,同时大大减轻了后续工作量。

图5 H=8 m和D=22 m时空区的破坏情况
3.1.2 塑性区及采场破坏特征分析
如图 6 所示,仅以尾砂堆积=0 m、境界顶柱=17 m时,不同跨度下采空区周边矿体及围岩的塑性区进行分析,图中反映了跨度为10,18,26和34 m的基本情况。塑性区的监测主要为当前剪切区shear-n以及当前拉应力区tension-n,由于模拟结果中tension-n面积很小,因此分析shear-n即可。由图6可知:1) 随着跨度增大,塑性区域不断增大;2) 两帮上部的塑性区域比顶板的区域大;3) 随着跨度的增加,跨度对于塑性区的作用变大,即跨度越大,每单位增加4 m跨度引起的塑性区域越大。

表2 1号监测点在不同采场跨度下曲线拟合结果
结合位移(图 4(d))和塑性区分析(图 6(d)),可以判定在尾砂堆高=0 m,=17 m,=34 m时,空区虽有部分塑性区域,但不会引起采场的破坏。
3.2 未填尾砂(h=0 m)、D=34 m,境界顶柱H(14≤ H≤35 m)不同时开挖模拟
由上可知:对于境界顶柱为17 m和34 m的空区可以不受破坏。随着境界顶柱高度的不断增大,空区在相同跨度情况下安全系数越高[13−15]。空区跨度14 m作为模拟对比,对于境界顶柱大于 17 m部分,进行跨度为 34 m的模拟,若出现某一空区严重破坏现象,立即停止模拟进行全面参数检验,并重新进行模型的模拟试验。模拟过程满足不平衡力始终小于= 5×10−6,根据模拟的矿体的极限抗拉强度 0.776 MPa,通过监测顶板拉应力计算出稳定性安全系数F。
根据表3分析,可以得出以下几点结论:
1) 在同一空区跨度情况下,各监测点的位移随着境界顶柱的增大而减小,且从表3加粗数据往下起,位移减小的速率逐渐减小,即在该位置出现了位移减小突变值(=20 m左右)。当≤14 m时,监测点位移和塑性区面积大,空区发生破坏;当 17≤≤20 m时,位移减小速率较大,说明顶柱高度对稳定性的影响较大;当 20≤≤ 35 m时,位移减小速率小,说明顶柱高度对采场空区稳定性的影响 减小。
床层复氧可采取数种方式加以强化:①干湿交替的间歇运行方式;②床内设置通气管进行自然或强制复氧;③利用植物的根系对系统内部进行复氧,这项研究国内外已有相关进展。

D/m:(a) 10;(b) 18;(c) 26;(d) 34

表3 不同境界顶柱高度下监测值情况及顶板稳定性情况
注:加粗数据表示该点数据变化速率较大,即“突变点”
2) 在相同的情况下,顶板拉应力都小于矿体极限抗拉强度 0.776 MPa。并随着的增大而减小,且在=20 m左右出现“突变”,该位置拉应力的减小速率最大,稳定性系数S达到了 1.77,该位置之后顶板拉应力随着的增大变化不大。即在=20 m左右,境界顶柱对于稳定性的影响较大,属于较安全稳定状态。
3) 在相同的情况下,塑性区面积(shear-n变形区)随着的增大而减小,并且在=20 m处的减小速率最大,该点的塑性区面积为 107.41 m2,为突变点。
综合考虑以上统计参数,在跨度达到 34 m的情况下,17~35 m的境界顶柱都不会导致采场的破坏,且在=20 m左右出现位移、拉应力、塑性区面积的突变,即在该位置境界顶柱高度对空区的稳定性的影响最大。结合矿山实际经济效益,可认为在不填尾砂的情况下,20 m的境界顶柱高度可以满足空区跨度为34 m以下采场的绝对稳定性。
3.3 境界顶柱H=20 m,尾砂回填过程模拟分析
尾砂回填是本次模拟的最后环节,也是最为重要的一部分,对于应用实践有很重要的现实意义,由于该步骤是一个动态过程,地下采矿受到的载荷也是渐变的过程,为了充分符合实际,本文采用尾砂逐层堆积模拟,分别进行 20,40,60,80,100,120,140,160,180和200 m模拟,同时对采场跨度D进行进一步研究,分别进行跨度为 10,14,18,22,26,30和34 m的情况进行模拟,监测平衡状态下关键点 1号和2号的各项情况。
表4 反映的是境界顶柱=20 m情况下,不同尾砂堆高对不同跨度采空区的影响,从表4可以看出:
1) 随着尾砂的堆高,不同跨度的空区顶板的垂直位移均有不同程度的上升趋势。其中跨度越大的采场表现的位移更大。尾砂堆积小于 120 m时,=26 m时出现了顶板位移的“突变”,即当跨度大于26 m时位移增大的速率明显增加,破坏的速率加快,故=26 m应该为该境界顶柱在尾砂堆积 120 m以下最合理的跨度;当尾砂堆积为 120~160 m时,“突变高度”为 12 m,即 18 m的跨度为尾砂堆积160 m时的合理长度,符合实际;同理,当堆高在 160 m以上时,最佳采场跨度应控制在 18 m左右。
2) 尾砂堆高 60 m时,跨度 34 m的采场开始破坏,至堆高 120 m时,跨度 30 m的采场开始破坏。跨度30 m以下的空区在堆高最大的 200 m时没有破坏。
由位移分析得,当境界顶柱一定时,随着尾砂不断堆高,相对较大的空区跨度采场会发生垮塌,合理的跨度会随着堆高的增加不断减小。同时,当堆高大于某一临界值后,尾砂对地下开采的影响将不断增大。
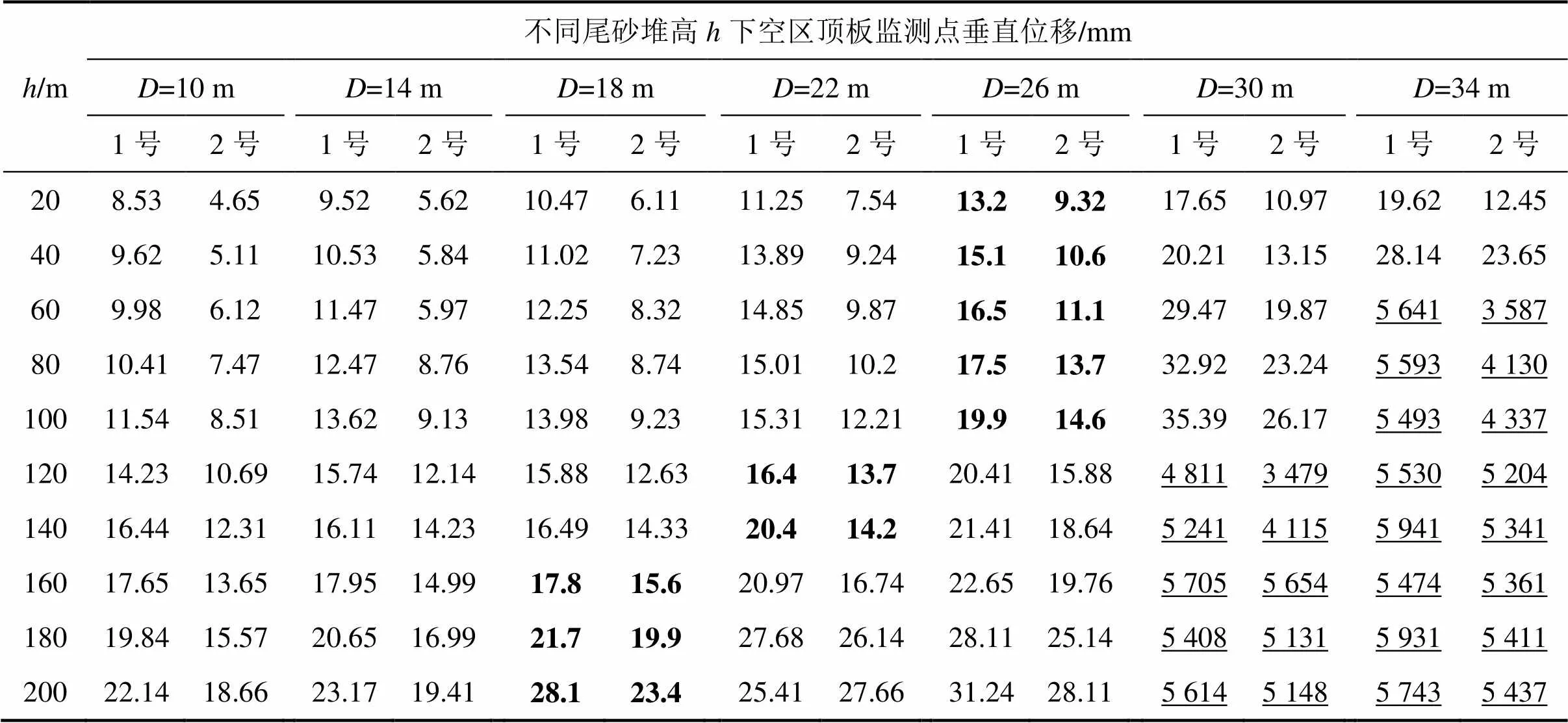
表4 不同尾砂高度下监测点位移情况
注:加粗数据表示该点数据变化速率较大,即“突变点”,下划线表示该数据对应的空区已经破坏。
3.4 尾砂回填对露天台阶影响模拟分析
3.4.1 位移分析
以=20 m,=26 m进行模拟,分析不同尾砂堆高对采空区影响。对比不同监测点的位移情况,发现监测点位移具有层次感(见图7)。在同一尾砂堆高下,空区顶板位移>露天坑台阶位移>深部矿体边界处位移。在堆积过程中,关键点的位移均有随着尾砂的堆高的增大而增大的趋势,且坑底的变形也逐渐增加,当尾砂堆积超过 160 m后,位移量变大明显,但整个系统仍保持平衡稳定状态。深部矿体边界8号监测点的位移始终保持在较低值,且有较小的波动增大趋势,深部地下作业的安全性较高,受尾砂堆积高度的作用不明显;浅部位置的位移较高,且有明显上升的趋势,故浅部的开采活动要注意预留矿柱以及顶底柱的保护。

图7 关键点竖向位移图
3.4.2 塑性区分析
图8所示为反映当尾砂堆积高度 200 m时露天坑整体的塑性区。
塑性区区域出现了较大的面积,且空区上方均已发生不同程度的塑性变形,上部位置局部发生贯通,顶板位置存在着垮塌危险;露天坑台阶位置也出现了较小范围的塑性区域,且随着深度的增加,塑性区区域有增大趋势,此时的采场参数对于地下开采有较大的风险,可以适当提高境界顶柱的高度或减小采场跨度作为调整。
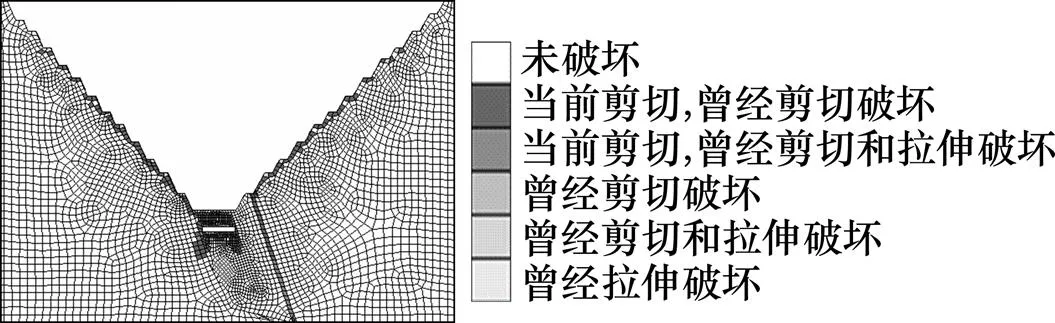
图8 整体shear-n变形区
4 结论
1) 同一采场跨度下,顶板关键点垂直位移随着境界顶柱的减小而增大,且在破坏前存在位移变化速率峰值(34 m跨度下,20 m顶柱高度位移变化最快)临界点;顶板塑性区面积随着境界顶柱的减小而增大,同样存在变化率峰值(=20 m),此时参数最符合矿山安全经济最大化。
2) 在同一境界顶柱高度下,随着尾砂堆积量的增大(=0~200 m),局部跨度较大的采场(跨度>30 m)出现破坏现象,关键点位移变化速率最大所对应的采场跨度随着的增大而减小,由原来的 26 m减小到 18 m,尾砂堆积对于跨度大的采场影响较跨度小的更大。当尾砂堆高<160 m时,堆高对于地下采矿的影响相对较小,关键点的位移以及监测区的塑性区变化速率小;当尾砂堆高>160 m时,关键点位移增大速率加快,需要适当调整采场参数或顶柱高度来提高安全性。
3) 尾砂排放导致露天坑台阶位移增大、塑性区变形较明显,且台阶深部塑性区要明显比浅部的大,与实际工程相符。
[1] 王新民, 赵建文, 张钦礼, 等. 露天转地下最佳开采模式[J]. 中南大学学报(自然科学版), 2012, 43(4): 1434−1439. WANG Xinmin, ZHAO Jianwen, ZHANG Qinli, et al. mining model of transition from open-pit to underground mining[J]. Journal of Central South University (Science and Technology), 2012, 43(4): 1434−1439.
[2] 李地元, 李夕兵, 赵国彦. 露天开采下地下采空区顶板安全厚度的确定[J]. 露天采矿技术, 2005(5): 17−20. LI Diyuan, LI Xibing, ZHAO Guoyan. Roof security thickness determination of underground goaf under open-pit mine[J]. Opencast Mining Technology, 2005(5): 17−20.
[3] 张亚宾. 露天采空区排尾对地下开采影响的研究[D]. 唐山: 河北理工学院资源与环境工程系, 2003: 32−54. ZHANG Yabin. Study of the influence on underground mining during stacking the gangue in open pit[D]. Tangshan: Hebei University of Technology. Department of Resource and Environment Engineering, 2003: 32−54.
[4] 夏世友. 露天坑回填对地下岩体的应力应变场影响研究[D]. 武汉: 武汉工程大学环境与城市建设学院, 2013: 32−77. XIA Shiyou. Study on the influence of open pit backfilling on underground rock mass stress and strain[D]. Wuhan: Wuhan Institute of Technology. School of Environment and Engineering, 2013: 32−77.
[5] Itasca Consulting Group, Inc.. FLAC3D(Fast Lagrangian Analysis of Continua in 3 Dimensions)Version 3.1,Users Guide[M]. Minnesota, USA: Itasca Consulting Group, Inc., 2006: 1−240.
[6] 史秀志, 黄刚海, 张舒, 等. 基于FLAC3D的复杂条件下露天转地下开采空区围岩变形及破坏特征[J]. 中南大学学报(自然科学版), 2011, 42(6): 1710−1718. SHI Xiuzhi, HUANG Ganghai, ZHANG Shu, et al. Goaf surrounding rock deformation and failure features using FLAC3Din underground mining shifted from open-pit in complex situation[J]. Journal of Central South University (Science and Technology), 2011, 42(6): 1710−1718.
[7] 邹友峰, 柴华彬. 我国条带煤柱稳定性研究现状及存在问题[J]. 采矿与安全工程学报, 2006, 23(2): 141−146. ZOU Youfeng, CHAI Huabin. Research status of strip coal pillar stability and its main problems in China[J]. Journal of Mining & Safety Engineering, 2006, 23(2): 141−146.
[8] 何忠明, 曹平. 考虑应变软化的地下采场开挖变形稳定性分析[J]. 中南大学学报(自然科学版), 2008, 39(4): 641−646. HE Zhongming, CAO Ping. Deformation and stability, analysis of underground stope after excavation considering strain softening[J]. Journal of Central South University (Science and Technology), 2008, 39(4): 641−646.
[9] DUNCAN J M. State of the art: Limit equilibrium and finite element analysis of slopes[J]. Journal of Geotechnical Engineering, ASCE, 1996, 122(7): 577−596.
[10] 闫长斌, 徐国元, 李夕兵, 等. 爆破震动对采空区稳定性影响的FLAC3D分析[J]. 岩石力学与工程学报, 2005, 24(16): 2894−2899. YAN Changbin, XU Guoyuan, LI Xibing, et al. Stability analysis of mined-out areas influenced by blasting vibration with FLAC3D[J]. Chinese Journal of Geotechnical Engineering, 2005, 24(16): 2894−2899.
[11] 谢和平, 周宏伟, 王金安, 等. FLAC在煤矿开采沉陷预测中的应用及对比分析[J]. 岩石力学与工程学报, 1999, 18(4) 397−401. XIE Heping, ZHOU Hongwei, WANG Jinan, et al. Application and contrastive analysis of FLAC in forecasting coal mining subsidence[J]. China Mining Magazine, 1998, 7(5): 37−41.
[12] 薛涛. 基于突变理论的露天矿复杂采空区稳定性研究[D]. 长沙: 中南大学资源与安全工程学院, 2012: 46−74. XUE Tao. Research on goaf stability of open pit mines based on catastrophe theory[D]. Changsha: Central South University. School of Resources and Safety Engineering, 2012: 46−74.
[13] 李夕兵, 李地元, 赵国彦, 等. 金属矿地下采空区探测、处理与安全评判[J]. 采矿与安全工程学报, 2006, 23(1): 24−29. LI Xibing, LI Diyuan, ZHAO Guoyan, et al. Detecting disposal and safety evaluation of the underground goaf in metal mines[J]. Journal of Mining & Safety Engineering, 2006, 23(1): 24−29.
[14] 李仲奎, 戴荣, 姜逸明. FLAC3D分析中的初始应力场生成及在大型地下洞室群计算中的应用[J]. 岩石力学与工程学报, 2002, 24(增刊): 2387−2392. LI Zhongkui, DAI Rong, JIANG Yiming. Improvement of the generation of the initial stress field by usingFLAC3D and application in a huge understand cavern group[J]. Chinese Journal of Rock Mechanics 2002, 24(Supp): 2387−2392.
[15] ZHOU Jian, LI Xibing, MITRI H S, et al. Identification of large-scale goaf instability in underground mine using particle swarm optimization and support vector machine[J]. International Journal of Mining Science and Technology, 2013, 23: 701−707.
(编辑 杨幼平)
Influence on underground mining stability of stope during stacking dry stacked Gangue in open-pit
CHEN Jiayao, SHI Xiuzhi, ZHOU Jian, QIU Xianyang, WANG Yang
(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)
In view of Tong-lü-shan underground mining shifted from open-pit using dry stacked Gangue technology, the numerical simulation software combined with the strength reduced methods and the displacement mutation characteristics of monitoring points was used to analyze failure features of goaf and stability safety coefficient under different heights of dry gangue. Feasibility analysis about stacking gangue was done. The results show that when there is no tailing loaded, the optimal thickness of boundary pillar is 20 m and the allowed spans are more than 34 m. The form of goaf failure is that both ends of roof are shear failure; When it begins to load tailings and the span is more than 30 m, the stope collapse and the area of rock’s plastic deformation is obvious; When the tailing loaded exceeds 160 m, the area of stope’s plastic zone and roof displacement rapidly increase, and the stacking gangue to the extent of goaf damage also increases considerably, which may further reduces the reasonable span of the stope.
tailings discharge into open-pit; crown pillar; underground stope stability; dynamical monitoring; numerical simulation
10.11817/j.issn.1672−7207.2017.10.023
TD 325
A
1672−7207(2017)10−2723−09
2016−10−10;
修回日期:2017−01−07
国家重点研发项目(2017YFC0602902)(Project (2017YFC0602902) supported by the National Key Research and Development Program of China)
史秀志,博士,教授,博士生导师,从事采矿与安全研究;E-mail:csublasting@163.com

