基于点过程模拟的时空级联模式统计挖掘方法
徐枫,陈袁芳,蔡建南,刘启亮,邓敏
基于点过程模拟的时空级联模式统计挖掘方法
徐枫,陈袁芳,蔡建南,刘启亮,邓敏
(中南大学地球科学与信息物理学院,湖南长沙,410083)
从时空统计的角度,将时空级联模式的频繁度评价建模为多元独立分布零假设下的显著性判别问题,提出一种基于点过程模拟的时空级联模式统计挖掘方法。首先,采用时空点过程模拟每类地理要素的观测数据集,构建显著性判别的零模型;其次,通过蒙特卡洛模拟获取零假设下每种候选时空级联模式频繁度的实验分布;最后,对候选模式的观测频繁度进行显著性检验,识别显著的时空级联模式。研究结果表明:本文方法能够用于有效识别地理要素间的时空级联模式,且避免了挖掘结果对频繁度阈值设置的依赖。
时空数据挖掘;时空级联模式;时空点过程;显著性检验
为了发现不同地理要素时空分布间的关联关系,人们对时空关联模式挖掘进行了研究[1−2]。时空级联模式是时空关联模式的一种重要表现形式,旨在描述不同地理要素频繁发生于邻近空间位置的时间先后顺序[3]。挖掘时空级联模式对于进一步揭示和理解不同地理要素间关联关系的传导机制具有重要价值,现已被广泛应用于公共安全、环境管理、公共卫生等领域[4]。例如,在公共安全领域,发现不同类型犯罪案件及其影响因素间的诱导机制,可为犯罪防控提供重要的决策信息[5]。时空关联模式主要包括时空同现模式和时空级联模式,前者刻画不同地理要素间的同现关系,后者在同现关系的基础上进一步描述邻近要素发生的先后顺序。现有时空关联模式挖掘方法大多是在空间关联模式挖掘模型[6−7]的基础上,通过施加时间邻近约束和时间次序约束,将地理要素间的关联关系从空间域扩展至时空域[8]。根据在挖掘模型中纳入时间约束的方式,将现有方法的研究策略大致分为时空分治和时空耦合共2类。时空分治策略将时空数据集划分为若干个时间切片上的空间数据集,首先挖掘每个时间切片上频繁满足空间邻近约束的空间关联模式,进而统计每个空间关联模式出现的时间切片个数,提取频繁的时空关联模式。例如,CELIK等[9]在每个时间切片上提取空间同现模式,将频繁出现在多个时间切片上的候选模式定义为时空同现模式。为了发现时空同现模式的时空演化规律,CELIK等[10]进一步提取了频繁度随时间持续增长的时空同现模式;QIAN等[11]首先识别每个时间片上若干空间子单元中的空间同现模式,进而提取同现模式随空间和时间的传播规律。时空耦合的策略则是采用时空耦合的搜索半径定义地理要素间的有向或无向的时空邻近关系,将频繁满足时空邻近关系的不同地理要素集合定义为时空关联模式。例如,WANG等[12]基于FP-growth算法提取频繁同时满足空间邻近和时间邻近的地理要素集合,并识别为时空同现模式。为了分析发现地理要素间关联关系的传递规律,HUANG等[13]将频繁按照形如1→2→…→n的链式顺序发生于邻近时空位置的多类地理要素集合识别为时空序列模式。除了发现邻近地理要素发生的全序关系外,MOHAN等[3]进一步识别地理要素发生的偏序关系即部分地理要素按全序顺序频繁发生于邻近时空位置,并定义为时空级联模式。相对于时空分治的策略,时空耦合策略避免了时间切片对地理要素间关联关系的割裂。时空分治的策略由于对连续时间域进行了离散化处理,会破坏地理要素在不同时间切片间关联关系,进而可能导致挖掘结果遗漏[14]。而时空耦合的策略能够很好地表达时空关联关系,但运行效率比时空分治策略的低。为此,QIAN等[14]将这2类策略纳入统一挖掘框架,通过变换滑动窗口大小,将这2类策略均转换为该框架下的特例。通过分析可以发现,现有方法多需要人为设置频繁度阈值,一般用户由于缺少先验知识,难以获得客观的挖掘结果。另外,在频繁度评价过程中,未顾及地理要素本身的分布特征,导致挖掘结果存在误差。针对这些问题,本文作者以时空级联模式为例,提出一种时空级联模式的统计挖掘方法。该方法无需人为设置频繁度阈值,也可准确识别地理要素间的时空级联模式。
1 研究策略
时空级联模式挖掘的关键在于候选模式频繁度的评价。采用人为设置的频繁度阈值筛选候选模式会导致结果遗漏或误判,因此,本文从时空统计的视角,将时空级联模式挖掘建模为多元独立分布零假设下候选模式频繁度的显著性判别问题,即判断候选模式在观测数据集中的频繁度与零假设为真时的频繁度是否存在显著性差异。
零假设下不同类型地理要素的时空分布相互独立,但每类地理要素应保持原有的分布特征[15]。在现实世界中,由于地理要素存在时空相关性,导致时空点模式分析中假定的完全随机分布不再适用[16]。因此,针对每类地理要素,本文首先对其分布特征进行分析,选择合理的点过程模型进行拟合,生成与其原始分布特征相似的模拟数据,进而构建时空级联模式显著性判别的零模型。针对每个候选模式,若零假设下得到大于或等于观测数据中频繁度的事件是1个小概率事件,则说明该候选模式中的地理要素不服从多元独立分布的零假设,将该候选模式定义为显著的时空级联模式。基于以上策略,本文方法主要包括2步:1) 多元独立分布的零模型构建;2) 时空级联模式的显著性判别。
2 时空级联模式统计挖掘方法
2.1 基于时空点过程模拟的零模型构建
为构建时空级联模式显著性判别的零模型,首先需要对每类地理要素的时空分布特征进行分析。针对每类地理要素f,采用时空函数[17]统计观测数据中一定搜索半径范围内时空点的个数,与完全随机分布下的理论函数值进行比较,进而判断该要素f是否存在显著的自相关特征。时空函数定义为

进一步,针对不同分布特征的地理要素,需要选取合理的时空点过程模型模拟其时空分布。若地理要素f存在时空自相关,则采用泊松簇过程[18]模拟其时空聚集分布过程,否则采用均匀泊松过程[18]进行模拟。对于每个地理要素f,采用牛顿迭代法[19]估计其时空点过程的模型参数。在每次迭代过程中,采用调整后的模型参数生成大量模拟数据,并据此计算该参数下时空函数的实验值,进而度量其与观测数据中时空函数值的差异,作为参数优化的目标函数,具体表达为
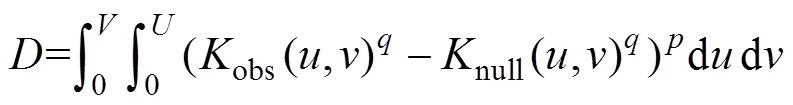
式中:obs(,)为观测数据中的时空函数值;null(,)为根据模拟数据计算的时空函数试验值;和分别为空间半径和时间半径的最大取值;和为调节因子(本文分别设置为1/4和2)。若小于一定阈值(本文设置为0.005),则停止迭代,返回最优的模型参数。
基于泊松簇过程的零模型构建如图1所示。从图1(b)可以看出该要素时空函数的观测值总大于理论值,表明其存在自相关特征,故采用泊松簇过程对其时空分布进行模拟,得到的模拟数据如图1(c)所示。从图1(d)可见:模拟数据中时空函数曲面与观测数据中的时空函数曲面基本吻合,说明模拟数据的时空分布能够较好地保持观测数据中的聚集特征。
2.2 时空级联模式的显著性检验
首先,阐述时空级联模式挖掘中一些相关概念,并给出如下定义[3]。
定义1 地理要素的实例。某类地理要素f在特定时间点出现在特定空间位置(,)的实体称为该地理要素的实例e。
定义2 有向邻域关系。给定空间半径R和时间半径R,若一地理要素实例e发生后的时间R内发生另一地理要素实例e,且与e的空间距离不超过R,则e与e满足有向邻域关系e→e。
定义3 时空级联模式及其实例。给定包含多个地理要素的时空数据集,类地理要素1,…,f的实例若频繁按照一定时间顺序出现在邻近空间位置(即频繁满足一定有向邻域关系),则类地理要素构成一个时空级联模式,如{1→2;1→3;2→4;3→4},类地理要素的实例中满足该有向邻域关系的集合称为该级联时空模式的实例。
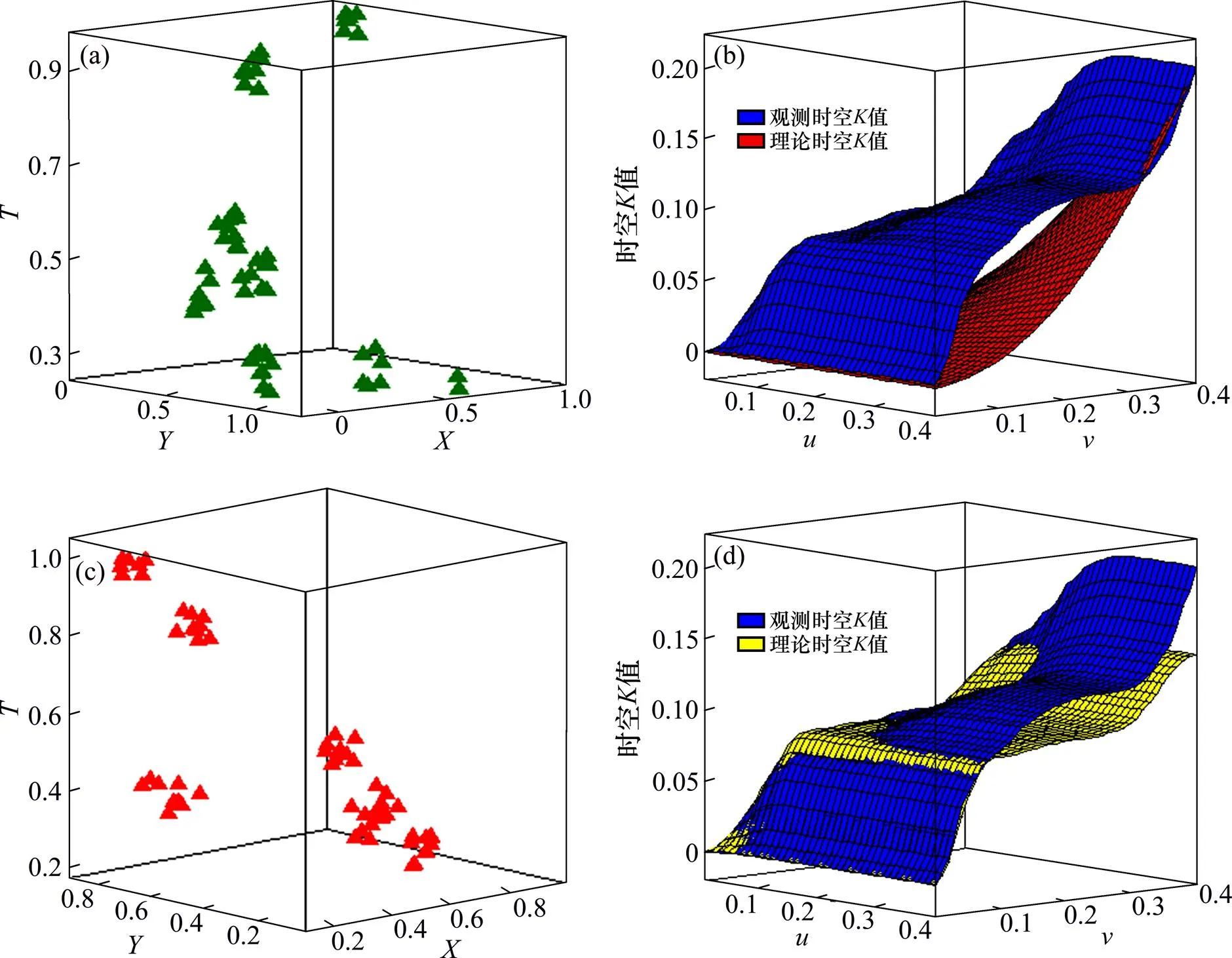
(a) 示例数据集;(b) 观测数据中的时空K函数值;(c) 模拟数据集;(d) 时空K函数的观测值与模拟值
定义4 级联参与指数。给定包含个地理要素1,…,f的时空级联模式,级联参与指数定义为

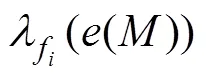
(a) 有向邻域关系;(b) 示例时空级联模式
图2 时空级联模式示意图
Fig. 2 Illustration of spatio-temporal cascading pattern
基于以上定义,将时空级联模式的频繁度度量指标(即级联参与指数)作为显著性检验的统计量,通过比较候选模式在零假设下频繁度的模拟分布与观测数据中频繁度的差异,对候选模式的频繁度进行客观评价。针对每个候选时空级联模式,显著性检验的具体步骤如下:
1) 在观测数据集中,计算该候选模式的级联参与指数,记为obs()。



进而,给定显著性水平,若该候选模式的显著性小于等于,则拒绝该模式中地理要素时空分布相互独立的零假设,将该候选模式识别为显著时空级联模式。
3 实验分析与应用
实验中,采用模拟数据和实际数据验证本文方法的有效性,并与现有的基于频繁度阈值的时空级联模式挖掘方法[3]进行比较。本文方法中,每类地理要素的时空分布分别模拟99次,显著性水平设为0.05。按照文献[3]建议,对该方法中级联参与指数的阈值设为0.2。
3.1 模拟实验
模拟数据集空间分布范围为[0,1]2的单元,时间分布范围为[0,1]的单元,如图3所示,分别采用具有不同分布特征的4组模拟数据(记为1,2,3和4)进行实验分析。1中,2类要素均具有大量实例,呈随机分布;2中,类要素具有大量实例,类要素实例数较小,但均预设在类要素的有向邻域内;3中,2类要素均有大量实例,呈聚集分布;4中,类要素具有大量实例,呈随机分布,类要素具有大量实例,呈聚集分布。除2外,其他模拟数据集中均无预设级联模式。
4组模拟数据中,时空级联模式{→}的频繁度评价结果见表1,可见采用本文方法所得结果与预设结果相吻合。1中,由于2类要素大量实例随机分布,导致现有方法中频繁度被高估,但本文方法发现2类要素间不存在显著的时空关联关系;2中,由于大量类要素的周围不存在类要素,因此,现有方法中频繁度小于所设阈值,但采用本文方法发现类要素显著依赖于类要素;3中,由于2类要素的时空簇存在随机交叠,导致现有方法中该模式具有较高频繁度,但采用本文方法发现2类要素的发生不存在显著依赖关系;4中,类要素的随机分布同样会导致现有方法发生误判,但采用本文方法也可判断2类要素间不存在显著关联关系。

(a) S1;(b) S2;(c) S3;(d) S4
通过分析可以发现:本文方法能够有效地避免一类要素分布对多类要素关联模式分析的干扰,同时也避免了频繁度阈值设置的主观性对挖掘结果的影响。下面将进一步采用实际犯罪数据集验证本文方法在实际应用中的有效性。

表1 模拟数据中时空级联模式{A→B}的挖掘结果
注:为级联参与指数;为时空级联模式的显著性。
3.2 实际应用
犯罪活动一直是严重威胁人类生命财产和社会公共秩序的社会现象,发现不同类型犯罪及其诱导因子间的关联关系对犯罪防控具有重要意义[20−22]。本文采用2014年波特兰地区的犯罪数据[23]进行应用分析。经数据重分类后,数据集中包含11类犯罪案件:盗窃(30 795个实例)、扰乱治安(2 881个实例)、涉毒案 (2 599个实例)、侵害(2 313个实例)、诈骗(543个实例)、造假(1 904个实例)、渉酒案(2 241个实例)、伤害罪 (3 236个实例)、抢劫(802个实例)、蓄意破坏(4 115个实例)和涉枪案(310个实例)。现有研究发现酒吧关闭事件常会触发犯罪案件的发生[24],因此,本实验以酒吧关闭事件为例,进一步分析各类犯罪案件与诱导因子间的时空级联模式。
在现实地理环境中,地理要素间的交互关系错综复杂,采用单一的邻域半径难以准确发现地理要素间的关联关系。因此,本文采用1 km的空间半径、从6~12 h、步长为1 h的时间半径构建犯罪数据集中的有向邻域关系。4个时间邻域下获得的部分结果见表2,不同时间半径下显著时空级联模式的数量分布见图4(a),不同显著时长的模式数量分布见图4(b)。分析挖掘结果可以发现:1) 时空级联模式中涉酒案和涉毒案多为其他案件的前件案件,说明该类案件对其他案件的发生具有一定的诱导作用;2) 部分时空级联模式的级联参与指数较小,现有方法采用较高的频繁度阈值难以有效发现,本文方法通过对频繁度显著性进行判别,可以准确识别有效模式;3) 随着时间半径增加,显著时空级联模式的数目逐渐增多,表明该数据集中不同犯罪案件及其诱导因子间多存在长期的影响关系。
下面以时空级联模式{涉酒案→扰乱治安;涉酒案→涉毒案;扰乱治安→涉毒案}为例,对2种方法的实验结果进行比较分析,如图5所示。从图5可见:波特兰中心城区存在大量酒吧(图5(a)),因而中心城区内涉酒案件较密集(图5(b)),同样导致涉毒案件和扰乱治安案件在中心城区也具有较高的发生率(图5(c)和(d))。除中心城区外,其他区域也发生大量的、分布相对离散的涉毒案件和扰乱治安案件,这些案件级联参数指数的绝对值较小,现有方法难以发现该模式,本文方法通过对3类案件的时空分布进行模拟,可以对该模式的频繁度进行客观评价,发现其在4个时间半径内均具有显著的级联关系。进而,政府和公安部门可以加大对涉酒案件的监管力度,对其他级联案件的发生进行间接防控。

表2 犯罪数据集中的部分显著时空级联模式
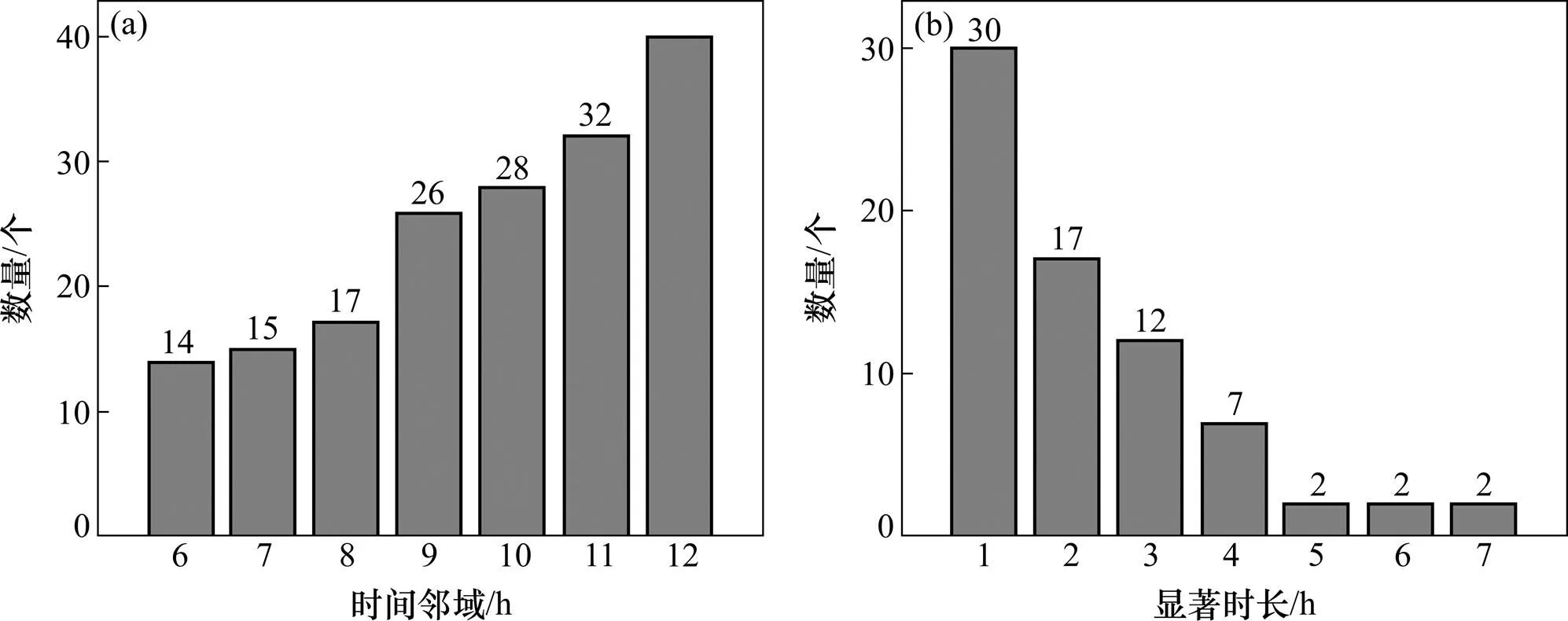
(a) 不同时间半径下的模式数量分布;(b) 不同显著时长的模式数量分布

(a) 酒吧关闭;(b) 涉酒案;(c) 涉毒案;(d) 扰乱治安
4 结论
1) 针对现有时空级联模式挖掘方法严重依赖于频繁度阈值设置的不足,将时空级联模式挖掘建模为多元独立分布零假设下候选模式频繁度的显著性判别问题,发展了一种时空级联模式的统计挖掘方法。
2) 与现有方法相比,本文方法能够有效识别地理要素间的时空级联模式,且无需人为设置频繁度阈值。降低了现有方法的主观性,并进一步提高了时空级联模式挖掘结果辅助案件侦查的可靠性。
[1] 李德仁, 王树良, 李德毅. 空间数据挖掘理论与应用[M]. 2版. 北京: 科学出版社, 2013: 1−10. LI Deren, WANG Shuliang, LI Deyi. Spatial data mining theories and applications[M]. 2nd ed. Beijing: Science Press, 2013: 1−10.
[2] SHEKHAR S, JIANG Z, ALI R, et al. Spatiotemporal data mining: a computational perspective[J]. ISPRS International Journal of Geo-Information, 2015, 4(4): 2306−2338.
[3] MOHAN P, SHEKHAR S, SHINE J A, et al. Cascading spatio-temporal pattern discovery[J]. IEEE Transactions on Knowledge & Data Engineering, 2012, 24(11): 1977−1992.
[4] CELIK M. Partial spatio-temporal co-occurrence pattern mining[J]. Knowledge and Information Systems, 2015, 44(1): 27−49.
[5] 叶文菁, 吴升. 基于加权时空关联规则的公交扒窃犯罪模式识别[J]. 地球信息科学学报, 2014, 16(4): 537−544. YE Wenjing, WU Sheng. Identifying crime patterns of bus pickpocket using weighted spatio temporal association rules mining[J]. Journal of Geo−information Science, 2014, 16(4): 537−544.
[6] HUANG Y, SHEKHAR S, XIONG H. Discovering colocation patterns from spatial data sets: a general approach[J]. IEEE Transactions on Knowledge & Data Engineering, 2004, 16(12): 1472−1485.
[7] 边馥苓, 万幼. k-邻近空间关系下的同位模式挖掘算法[J]. 武汉大学学报(信息科学版), 2009, 34(3): 331−334. BIAN Fuling, WAN You. A novel spatial co-location pattern mining algorithm based on k-nearest feature relationship [J]. Geomatics and Information Science of Wuhan University, 2009, 34(3): 331−334.
[8] 柴思跃, 苏奋振, 周成虎. 基于周期表的时空关联规则挖掘方法与实验[J]. 地球信息科学学报, 2011, 13(4): 455−464. CHAI Siyue, SU Fenzhen, ZHOU Chenghu. Period table based spatio-temporal association rules mining[J]. Journal of Geo-information Science, 2011, 13(4): 455−464.
[9] CELIK M, SHEKHAR S, ROGERS J P, et al. Mixed-drove spatio-temporal co-occurence pattern mining: a summary of results[C]//Proceedings of the 6th International Conference on Data Mining. Hong Kong, China, 2006: 119−128.
[10] CELIK M, SHEKHAR S, ROGERS J P, et al. Sustained emerging spatio-temporal co-occurrence pattern mining: a summary of results[C]//Proceedings of the 18th IEEE International Conference on Tools with Artificial Intelligence. Arlington, Virginia, USA, 2006: 106−115.
[11] QIAN F, HE Q, HE J. Mining spread patterns of spatio-temporal co-occurrences over zones[C]//International Conference on Computational Science and Its Applications. Heidelberg: Springer, 2009: 677−692.
[12] WANG J, HSU W, LEE M L. A framework for mining topological patterns in spatio−temporal databases[C]// Proceedings of the 14th ACM International Conference on Information and Knowledge Management.Bremen, Germany, 2005: 429−436.
[13] HUANG Y, ZHANG L, ZHANG P. A framework for mining sequential patterns from spatio-temporal event data sets[J]. IEEE Transactions on Knowledge and Data Engineering, 2008, 20(4):433−448.
[14] QIAN F, YIN L, HE Q, et al. Mining spatio-temporal co-location patterns with weighted sliding window[C]// IEEE International Conference on Intelligent Computing and Intelligent Systems. Shanghai, China, 2009: 181−185.
[15] DIGGLE P J. Statistical analysis of spatial point patterns[M]. 2nd ed. London, U.K.: Arnold, 2003: 30−40.
[16] ILLIAN J, PENTTINEN A, STOYAN H, et al. Statistical analysis and modelling of spatial point patterns[M]. Hoboken, NJ, USA: Wiley, 2008: 311−323.
[17] DIGGLE P J, CHETWYND A G, HÄGGKVIST R, et al. Second-order analysis of space-time clustering[J]. Statistical Methods in Medical Research, 1995, 4(2): 124−136.
[18] DIGGLE P J. Statistical analysis of spatial and spatio-temporal point patterns[M]. Boca Raton, FL, USA: CRC Press, 2013: 101−110.
[19] BYRD R H, LU P, NOCEDAL J, et al. A limited memory algorithm for bound constrained optimization[J]. Siam Journal on Scientific Computing, 1995, 16(5):1190−1208.
[20] ROSSMO D K. Geographic profiling[M]. CRC press. Boca Raton, FL, USA: 1999: 111−122.
[21] 姜超, 唐焕丽, 柳林. 中国犯罪地理研究述评[J]. 地理科学进展, 2014, 33(4): 561−573.JIANG Chao, TANG Huanli, LIU Lin. Review of crime geography in China[J]. Progress in Geography, 2014, 33(4):561−573.
[22] 祝晓光. 论犯罪地理学[J]. 人文地理, 1989, 4(2): 40−46. ZHU Xiaoguang. A discussion on the geography of crime[J]. Human Geography, 1989, 4(2): 40−46.
[23] Portland crime dataset[EB/OL]. [2016−10−15] http://www. civicapps.org/datasets.
[24] SCOTT M S, DEDEL K.Assaults in and around bars[M]. 2nd ed. Washington, DC: Office of Community Oriented Policing Services, 2006: 4−10.
(编辑 陈灿华)
A statistical approach for discovering spatio-temporal cascading patterns based on point process simulation
XU Feng, CHEN Yuanfang, CAI Jiannan, LIU Qiliang, DENG Min
(School of Geosciences and Info-physics, Central South University, Changsha 410083, China)
The discovery of spatio-temporal cascading patterns was modeled as a significance test for prevalence of candidate patterns under the null model of independence, and a statistical approach based on point process simulation was proposed. Firstly, null model was constructed by simulating the point process of different features. Then, the empirical distribution of prevalence of each candidate pattern was estimated by using Monte Carlo simulation. Lastly, significant spatio-temporal cascading patterns were identified by performing the significant test for the observed prevalence. The results show that the approach can effectively detect the meaningful spatio-temporal cascading patterns without threshold of prevalence measure.
spatio-temporal data mining; spatio-temporal cascading patterns; spatio-temporal point process; significance test
10.11817/j.issn.1672−7207.2017.10.022
P208
A
1672−7207(2017)10−2715−08
2017−04−21;
修回日期:2017−06−22
国家自然科学基金资助项目(41471385);湖南省自然科学杰出青年基金资助项目(14JJ1007)(Project(41471385) supported by the National Natural Science Foundation of China; Project(14JJ1007) supported by the Science Foundation for Distinguished Young Scholars of Hunan Province)
蔡建南,博士,从事时空关联模式挖掘研究;E-mail:jiannan.cai@csu.edu.cn
—— “T”级联

