冲击诱导损伤岩石的切削特性
吴万荣,娄磊,梁向京
冲击诱导损伤岩石的切削特性
吴万荣1, 2,娄磊1, 2,梁向京1, 2
(1. 中南大学高性能复杂制造国家重点实验室,湖南长沙,410083;2. 中南大学机电工程学院,湖南长沙,410083)
为了提高硬岩矿山开采时牙轮切削钻孔效率,降低钻具磨损,提出冲击诱导切削复合破岩新方法。在Walsh模型的基础上,建立冲击诱导孔周围岩石损伤区的裂纹模型,推导岩石损伤区的牙轮钻齿侵入系数方程及牙轮钻速方程,分析裂纹密度和扰动频率分别对岩石弹性模量、钻齿侵入系数和钻齿切削力的影响。研究结果表明:随着裂纹密度增大,岩石的有效弹性模量减小,侵入系数逐渐减小;在一定内摩擦角范围内,随着裂纹密度增大,牙轮钻速显著提高;在相同轴向载荷条件下,随着冲击扰动频率增大,牙轮钻齿切削力逐渐减小。
牙轮钻;冲击诱导;裂纹密度;侵入系数
在大型露天矿山开采中,常采用大直径牙轮钻机钻孔作业。然而,对于较硬金属矿山的开采,牙轮钻齿磨损严重,效率较低。为此,本文作者提出冲击诱导切削复合破岩的新工艺。冲击诱导孔周围岩石的应力重分布会造成岩石内部裂纹迅速扩展、导致其强度减小[1−3],从而更有利于切削破岩。为了研究诱导损伤区岩石内部裂纹对其切削特性的影响,必须建立冲击诱导损伤区域岩石裂纹模型及钻齿切削模型。DAVID等[4]建立了岩石的裂纹模型,但其并未对冲击扰动条件下裂纹的力学特性进行分析。李玮等[5−7]分析了钻井底部空隙压力及钻井液循环产生的附加压力对牙轮钻头钻速的影响,但其并未考虑扰动裂纹对牙轮钻速的影响。目前,对扰动破岩的研究主要是从动静组合加载的角度对岩石的宏观强度[8−11]及能耗机制[12−15]进行了相关分析,而对冲击扰动下产生诱导裂纹岩石的切削特性研究较少。为此,本文作者建立冲击诱导损伤岩石内部的裂纹模型,分析裂纹在“切削载荷+冲击扰动载荷”下的力学特性,建立牙轮钻头在冲击诱导损伤区的钻速方程,获得硬岩在冲击扰动载荷下的切削特性变化规律。
1 冲击诱导破岩原理
冲击诱导凿岩原理如图1所示(其中,为施加的轴向压力,为冲击载荷,为回转切削力矩)。其工作原理如下:冲击钻头在冲击活塞的作用下冲击钻凿中心孔,冲击诱导中心孔周围的岩石在原岩应力及冲击扰动载荷的作用下产生裂纹,使岩石强度弱化;同时,牙轮钻头对冲击诱导孔周边岩石施加旋转切削力,使岩石切削破碎。图2所示为单牙齿侵入诱导冲击孔周围岩石强度弱化区的载荷分析(其中,0为诱导冲击孔半径,为钻齿侵入半径,1为冲击诱导孔周围岩石强度弱化区半径);图3所示为单钻齿切削损伤岩石的受力分析(其中,′为剪切面上的法向应力,′为剪切面上的切向应力,为牙齿刃尖角,为侵入深度,′为剪切破坏面长度,c为裂纹闭合临界角,s为裂纹滑移临界角,为剪切破坏面与孔底平面的夹角)。

1—冲击活塞;2—牙轮钻头;3—冲击钻头;4—诱导损伤区岩石;5—冲击破碎区岩石。

图2 冲击诱导破岩时载荷分布
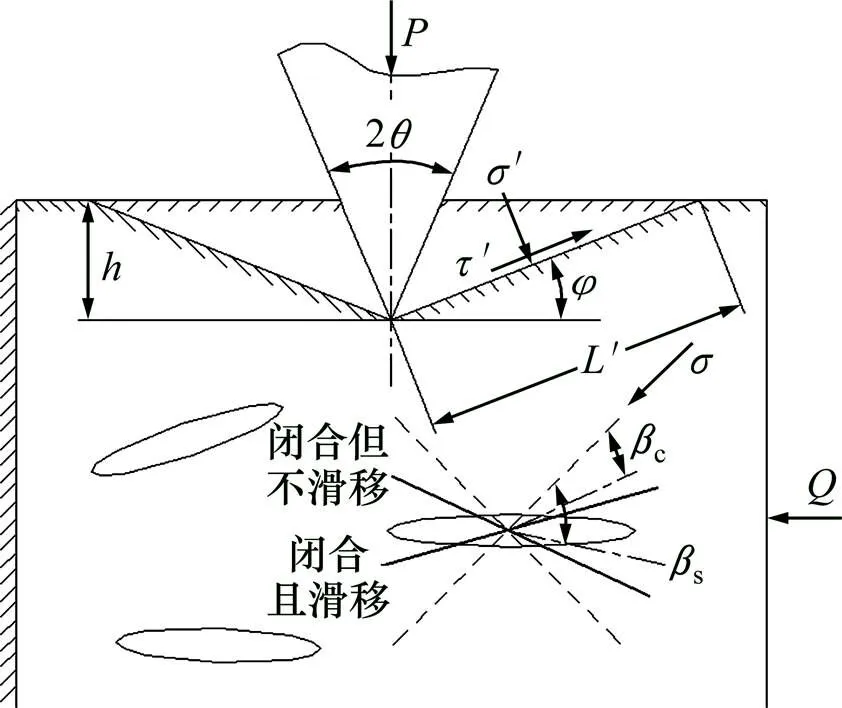
图3 单钻齿切削诱导损伤岩石的受力分析
2 冲击诱导损伤岩石的弹性模量及切削速度分析
2.1 冲击诱导损伤岩石的弹性模量分析
假设含个大小、方向相同且相互独立的裂纹,裂纹的长轴半径为,由图3可知单个裂纹受的压缩合力为
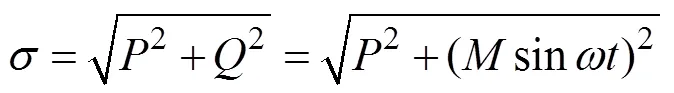
其中:为轴向压力;为冲击载荷;为冲击频率;为冲击幅值。
离散元模型中岩石的宏观参数和微观参数关系如下[16]:

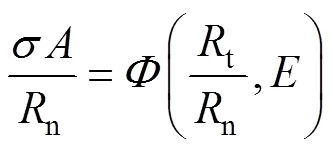






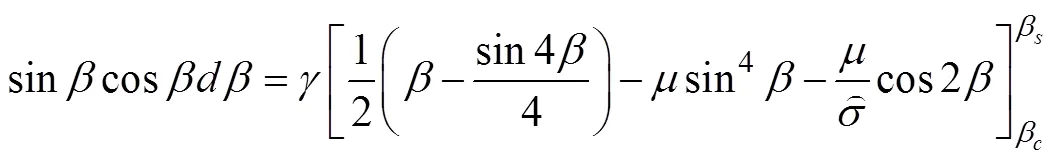
其中:c为裂纹闭合临界角;s为滑移临界角。
在冲击加载阶段,逐渐达到最大值max。之后,在冲击卸载阶段,逐渐由max卸荷至某一载荷′,其值为′=max−Δ。Δ将使裂纹受的剪切力减小Δ,并将使裂纹上下表面间的摩擦阻力减小Δf。当满足式(10)时,裂纹将发生反向滑移:

故裂纹发生反向滑移的条件为
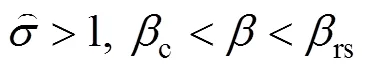

故在冲击卸载阶段,发生反向滑移裂纹的柔度为

在冲击卸载阶段含裂纹岩石的归一化弹性模量为

2.2 冲击扰动载荷作用下钻齿侵入系数及钻速方程
载荷和冲击载荷在岩石剪切破坏面上产生的法向应力′和剪切应力′为:


根据摩尔−库仑准则,诱导损伤区岩石发生剪切破坏的条件为

式中:为不含裂纹岩的石内聚力;′为含裂纹岩石的内聚力;为岩石内摩擦角。将式(15)和(16)代入式(17)得

式中:为内摩擦因数。对式(18)求导,并整理得

式中:为侵入系数,


考虑扰动裂纹时,单位时间内含个钻齿的牙轮钻头的机械钻速方程为
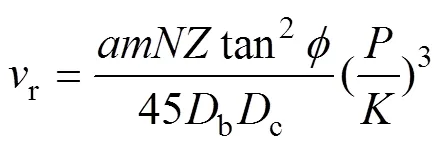
式中:r为牙齿的机械钻速;为多齿联合破岩系数;为钻齿个数;为钻头转速;为钻头外排齿圈个数;b为钻头直径;c为牙轮直径。
3 仿真及实验分析
仿真模型及实验系统原理如图4所示。仿真软件采用PFC软件,仿真原理如图4(a)所示。牙轮钻具切削岩石时,岩石的右端固定,左端施加一定的扰动载荷。仿真参数为:n=150 N,t=121 N,n=t=3.6 MN/m,=0.5。试验系统原理如图4(b)所示。
冲击扰动载荷由冲击扰动油缸9产生,轴向载荷由加压油缸10产生,回转切削载荷由回转切削马达11产生,通过压力传感器6测得结果计算得出相应的载荷。试验岩石为花岗岩,其物理力学参数如下:体积密度为2.640 t/m3,抗压强度为164.8 MPa,弹性模量为6.7×1010MPa,试样长×宽×高为1 000 mm×660 mm×540 mm。试验前,用砂轮机将岩石表面打平磨光,然后依次进行冲击频率为0,10和15 Hz的冲击钻孔作业,冲击诱导孔径为100 mm,孔深为500 mm。然后,用单牙轮钻头在冲击诱导孔周边进行切削实验,在相同轴向载荷条件下,测量回转切削马达的工作压力,进而计算牙轮钻头回转切削力。仿真及实验结果见图5~7。

(a) 仿真模型;(b) 实验系统原理


(a) 归一化弹性模量随归一化应力变化曲线;(b) 归一化应力随归一化应变曲线
图6所示为不同裂纹密度下侵入系数及牙轮钻速随随内摩擦角的变化曲线。从图6(a)可知:在相同裂纹密度下,岩石的侵入系数随内摩擦角增大呈指数增大;在相同内摩擦角条件下,岩石侵入系数随裂纹密度增加而减小。故含高裂纹密度的岩石,在相同牙齿机械参数条件下更易被侵入破碎。从图6(b)可知:当裂纹密度一定时,随岩石内摩擦角增大,机械钻速先增大后减小;当内摩擦角一定时,随着裂纹密度的增加,机械钻速明显增大,即在冲击诱导孔周围含裂纹岩石的机械钻速明显高于远离诱导孔区域的机械钻速。
图7所示为不同冲击扰动频率作用下,冲击诱导孔周围岩石切削力的仿真和实验曲线。由图7可知:随着冲击诱导频率增加,冲击诱导孔周边岩石的切削力明显减少,这说明随冲击诱导频率增大,诱导孔周边岩石的裂纹密度增大,从而更容易使岩石破碎。此外,在相同扰动频率下,仿真结果较实验结果小,其相对误差为25%左右,这是由于在仿真时,采用的裂纹密度与实际冲击诱导产生的裂纹密度有误差。
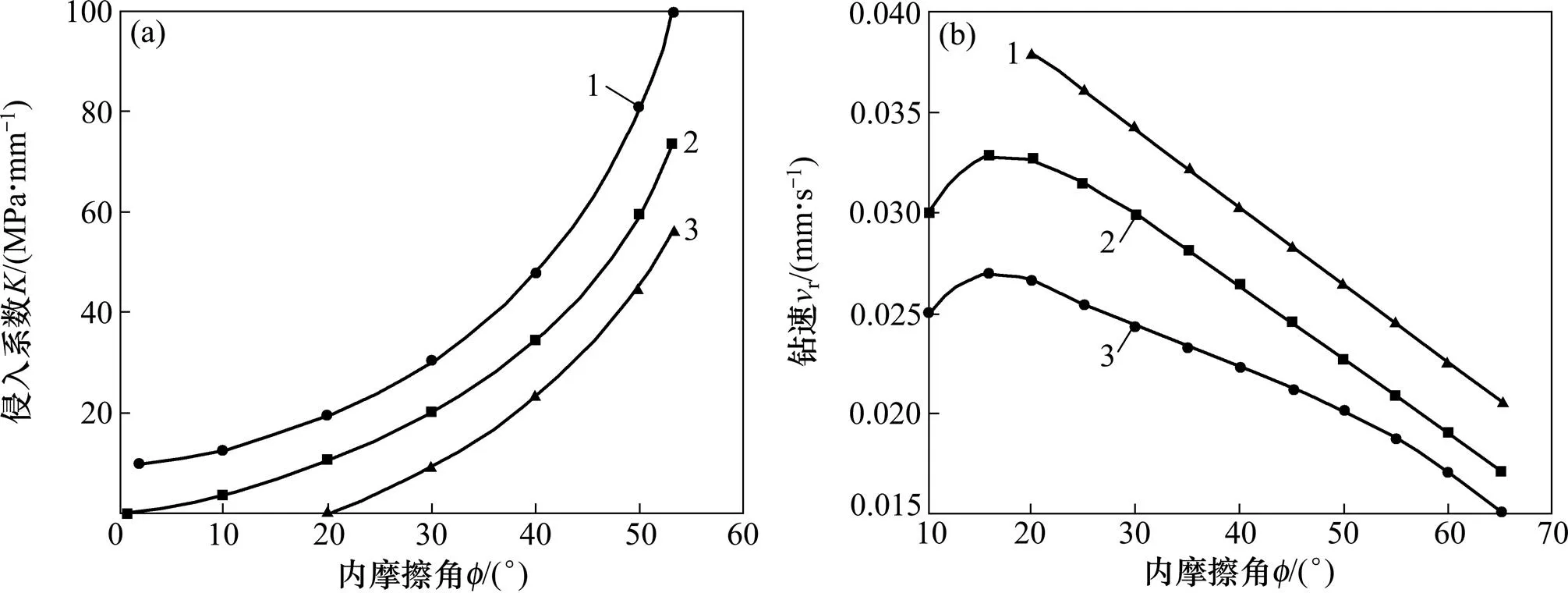
(a) 侵入系数随内摩擦角变化曲线;(b) 钻速随内摩擦角变化曲线

(a) 仿真曲线;(b) 实验曲线
4 结论
1) 随着岩石裂纹密度增大,岩石的有效弹性模量逐渐减小。
2) 随岩石裂纹密度增大,岩石的侵入系数减小,钻头的钻速明显增加。
3) 冲击扰动频率的增加有利于裂纹的产生,从而使岩石更易破碎。扰动频率为15 Hz的切削力约为无扰动时切削力的1/3。
[1] 李夕兵, 姚金蕊, 杜坤. 高地应力硬岩矿山诱导致裂非爆连续开采初探-以开阳磷矿为例[J]. 岩石力学与工程学报, 2013, 32(6): 1101−1111. LI Xibing, YAO Jinrui, DU Kun. Preliminary study for induced fracture and non-explosive continuous mining in high-geostress hard rock mine:a case study of Kaiyang Phosphate Mine[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(6): 1101−1111.
[2] 宫凤强, 陆道辉, 李夕兵, 等. 动力扰动下预静载硬岩断裂的增韧和减韧效应[J]. 岩石力学与工程学报, 2014, 33(9): 1905−1915. GONG Fengqiang, LU Daohui, LI Xibing, et al. Toughness increasing or decreasing effect of hard rock fracture with pre-static loading under dynamic disturbance[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(9): 1905−1915.
[3] LI Xibing, WANG Shiming, WENG Lei, et al. Damage constitutive model of different age concretes under impact load[J]. Journal of Central South University, 2015, 22(6): 693−700.
[4] DAVID E C, BRANTUT N, SCHUBNEL A, et al. Sliding crack model for nonlinearity and hysteresis in the uniaxial stress–strain curve of rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2012, 52(9): 9−17.
[5] 李玮, 郑浩然, 开月, 等. 基于单齿侵入理论的牙轮钻头钻速方程[J]. 东北石油大学学报, 2013, 37(1): 85−90. LI Wei, ZHENG Haoran, KAI Yue, et al. Drilling rate equation of cone bit based on single tooth intrusive theory[J]. Journal of Northeast Petroleum University, 2013, 37(1): 85−90.
[6] 李玮, 许兴华, 闫铁, 等. 欠平衡下牙轮钻头牙齿侵入系数及钻速研究[J]. 西南石油大学学报(自然科学版), 2013, 35(3): 168−173. LI Wei, XU Xinghua, YAN Tie, et al. Study on the tooth invasion coefficient of cone bit and penetration rate in under-balance drilling[J]. Journal of Southwest Petroleum University(Science and Technology Edition), 2013, 35(3): 168−173.
[7] 李玮, 李亚楠, 陈世春, 等. 井底牙轮钻头的钻速方程及现场应用[J]. 中国石油大学学报, 2013, 37(3): 74−77. LI Wei, LI Yanan, CHEN Shichun, et al. Drilling rate model of cone bit in bottom hole and field application[J]. Journal of China University of Petroleum, 2013, 37(3): 74−77.
[8] 殷志强, 李夕兵, 尹土兵, 等. 高应力岩石围压卸载后动力扰动的临界破坏特性[J]. 岩石力学与工程学报, 2012, 31(7): 1355−1362. YIN Zhiqiang, LI Xibing, YIN Tubing, et al. Critical failure characteristics of high stress rock induced by impact disturbance under confining pressure unloading[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(7): 1355−1362.
[9] YIN Zhiqiang, LI Xibing, JIN Jiefang, et al. Failure characteristics of high stress rock induced by impact disturbance under confining pressure unloading[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(3): 175−184.
[10] 左宇军, 马春德, 朱万成, 等. 动力扰动下深部开挖洞室围岩分层断裂破坏机制模型试验研究[J]. 岩土力学, 2011, 32(10): 2929−2936. ZUO Yujun, MA Chunde, ZHU Wancheng, et al. Model test study of mechanism of layered fracture within surrounding rock of tunnels in deep stratum tunnelling under dynamic disturbance[J]. Rock and Soil Mechanics, 2011, 32(10): 2929−2936.
[11] ZHU W C, LI Z H, ZHU L, et al. Numerical simulation on rockburst of underground opening triggered by dynamic disturbance[J]. Tunnelling and Underground Space Technology, 2010, 25(5): 587−599.
[12] 曹文卓, 李夕兵, 周子龙, 等. 高应力硬岩开挖扰动的能量耗散规律[J]. 中南大学学报(自然科学版), 2014, 45(8): 2759−2767. CAO Wenzhuo, LI Xibing, ZHOU Zilong, et al. Energy dissipation of high-stress hard rock with excavation disturbance[J]. Journal of Central South University (Science and Technology), 2014, 45(8): 2759−2767.
[13] 邹洋, 李夕兵, 周子龙, 等. 开挖扰动下高应力岩体的能量演化与应力重分布规律研究[J]. 岩土工程学报, 2012, 34(9): 1677−1684. ZOU Yang, LI Xibing, ZHOU Zilong, et al. Energy evolution and stress redistribution of high-stress rock mass under excavation distribution[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(9): 1677−1684.
[14] 蔡美峰, 冀东, 郭奇峰. 基于地应力现场实测与开采扰动能量积聚理论的岩爆预测研究[J]. 岩石力学与工程学报, 2013, 32(10): 1973−1980. CAI Meifeng, JI Dong, GUO Qifeng. Study of rockburst prediction based on in-situ stress measurement and theory of energy accumulation caused by mining disturbance[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(10): 1973−1980.
[15] 卢爱红, 茅献彪, 赵玉成. 动力扰动诱发巷道围岩冲击失稳的能量密度判据[J]. 应用力学学报, 2009, 25(4): 602−607. LU Aihong, MAO Xianbiao, ZHAO Yucheng. Criterion of impact instability of laneway under dynamic disturbance[J]. Chinese Journal of Applied Mechanics, 2008, 25(4): 602−607.
[16] ROJEK J, ONATE E, LABRA C, et al. Discrete element simulation of rock cutting[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(5): 996−1010.
(编辑 陈灿华)
Cutting features of damage rock by shock disturbance
WU Wanrong1, 2, LOU Lei1, 2, LIANG Xiangjing1, 2
(1. State Key Laboratory of High Performance Complex Manufacturing,Central South University, Changsha 410083, China;2. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)
In order to improve the drilling efficiency and reduce tools wear, a new rock fragmentation method of shock disturbance was presented. Based on the theory of Walsh, the crack model of the damaged rock around the induced hole was established, the intrusive coefficient equation of cone bit was derived, and the drilling rate model around the induced hole was built. The influence of crack density and the disturbance frequency on the elastic modulus, intrusive coefficient and the cutting force was studied. The results show that with the increase of crack density, the effective elastic modulus decreases and the intrusive coefficient decreases. Under a certain range of internal friction angle, the penetration rate increases obviously with the increase of the crack density. Under the condition of certain axial load, the cutting force of the one-cone bits decreases obviously with the increase of the disturbance frequency.
one-cone bits; shock disturbance; crack density; intrusion coefficient
10.11817/j.issn.1672−7207.2017.10.021
O347
A
1672−7207(2017)10−2709−06
2016−10−21;
修回日期:2016−12−22
国家自然科学基金资助项目(51774340);高性能复杂制造国家重点实验室基金资助项目(zzyjkt2015-03) (Project(51774340) supported by the National Natural Science Foundation of China; Project(zzyjkt2015-03) supported by the State Key Laboratory of High Performance Complex Manufacturing)
吴万荣,博士,教授,博士生导师,从事机电液一体化及高效钻孔装备研究;E-mail:zgloulei@163.com

