基于GPU的小尺寸FFT在实时图像复原中的优化

严发宝，苏艳蕊，赵占锋，左颢睿，柳建新



基于GPU的小尺寸FFT在实时图像复原中的优化

严发宝1，苏艳蕊1，赵占锋2，左颢睿3，柳建新4

(1. 山东大学(威海) 机电与信息工程学院，山东威海，264209；2. 哈尔滨工业大学(威海) 信息工程研究所，山东威海，264209；3. 中国科学院光电技术研究所，四川成都，610209；4. 中南大学地球科学与信息物理学院，湖南长沙，410083)

为满足跟踪识别系统对图像复原的实时性需求，在图形处理器(GPU)上进行高效实现小尺寸二维FFT的优化策略研究。首先对二维FFT算法进行分析，根据图形处理器的特点，提出基于图形处理器的并行执行模型。基于该模型，从算法的复杂度、跳转指令的数量、共享存储器的访问冲突以及共享存储器的访问延迟及图形处理器的利用效率这4个方面进行优化策略的研究，提出相应的优化方法。在图像复原的实验中，先对基于GPU的小尺寸FFT优化方法与基于CPU的MATLAB传统算法进行计算精度对比，然后基于4种不同尺寸的图像在相同的GPU平台上再与NVIDIA公司提供CUFFT函数库复原算法进行计算效率对比。研究结果表明：该优化方法提供的图像复原算法复原效果好，与MATLAB效果图比较人眼观察不出差异；在计算速率上，提出的优化方法能够在19.6 ms内复原1帧128×128灰度模糊图像，计算速度与直接采用CUFFT函数库算法相比提高约1.8倍。

图形处理器；小尺寸FFT；图像复原；并行优化；实时处理

图像复原在目标跟踪、目标识别系统中有着重要的应用，但图像复原算法特别是盲图像复原算法对退化图像均需要大量的二维快速傅里叶变换(二维FFT)迭代计算[1−4]。二维FFT的数值计算量大、数据依赖性强，同时具有计算密集型和存储密集型的特点，在常规处理平台如FPGA，DSP和通用CPU上难以满足高速二维信号处理的需求, 因此，采用更高处理能力的图形处理器(graphic process unit，GPU)成为当前研究的趋势[5−8]。GPU能够直接进行单精度和双精度浮点计算，在图像处理、雷达信号处理、物理建模等领域中有着广泛的应用[9−13]。ZHANG等[1−3]提出了噪杂退化图像的盲解卷积及基于乘性迭代算法的多帧盲图像复原，分别实现了高分辨率的图像复原与多帧图像的高分辨率复原；作为图像复原情况的一种，ZHANG等[1−3]提出的基于GPU像素级优化去雾准则实时单帧图像去雾方法，以80帧/s的速率去处理百万像素的大雾照片，效果优良，同时该方法受非均匀照明的影响比传统方法小；XIE等[5]提出的基于GPU的中频盲图像复原并行算法有效地提升了操作速率和复原的实时性；常方正等[8]提出的基于CUDA的遥感影像CVA变化检测方法与传统效果相比效率提高10倍左右；张全等[4]采用相位差算法对尺寸为256×256的图像进行50次迭代，50次迭代单GPU与双GPU分别耗时53 ms与45 ms，为目前搜索到的最高计算效率。实际中图像复原计算度复杂，迭代次数要远超50次，计算数据量大，而且53 ms远远低于所需实时性，实时图像复原通常在原图上选取特定区域实施，通常不大于256×256，即使缩小了处理图像的尺寸，在GPU上采用目前已有的计算方法，仍不能满足工程中对图像复原的实时需求[14]。为此，本文作者探讨如何在GPU上高效实现小尺寸二维FFT的方法，并应用到实时图像复原处理中。

1 DFT与二维FFT计算流程

1.1 DFT算法

一维点向量对应的函数()的正反离散傅里叶变换(DFT)公式为[15]：

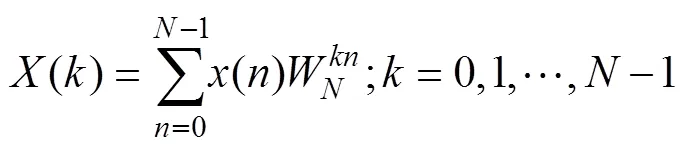
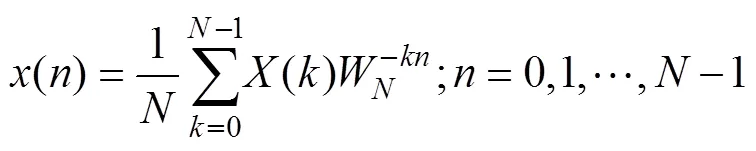
1.2 二维FFT计算流程

FFT算法是傅里叶算法的快速计算方法，详细计算方法见文献[16−17]。图像的数字化一般都是用二维矩阵进行描述，这里只介绍二维FFT计算的步骤，对于输入矩阵(，)，具体的计算流程如图1所示。

图像数据的二维矩阵(，)输入到处理器，首先对矩阵中的行一维数据进行FFT计算，即

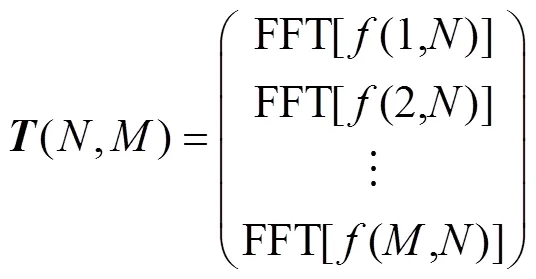
得到一维计算结果(，)后，需要进行FFT计算结果倒位序计算，得到1(，)，然后进行转置 计算：

再对矩阵(，)进行如式(3)一样的一维计算，得到2(，)，然后对该矩阵进行倒位序计算后，转置得到最后的二维FFT计算结果(，)。

图1 二维FFT计算流程图

2 GPU上的二维FFT计算

2.1 算法并行特征分析

二维矩阵(，)的FFT的计算主要由一维FFT构成，主要分析一维点(=2)FFT的可并行性。

计算分为层，第层计算需要−1层的计算结果(1＜≤)，层与层之间的计算只能串行；

每层中参与计算的数据均为个，每层的计算次数一样，每一层内的计算可以并行执行；

旋转因子W根据输入点序号进行计算，任意点之间没有相关性，具有良好的可并行性；

二维FFT计算由多个一维FFT计算构成，一维FFT之间的计算是相互独立的，具有良好的可并行性。

2.2 算法并行计算模型

根据2.1节的分析，二维FFT计算具有较好的可并行性，能够较好地利用GPU的并行计算能力，图2所示为在GPU上对1个×的二维矩阵执行二维FFT的并行化模型。

1) 并行任务划分。对于×的二维矩阵，要进行+次一维FFT计算，以次点一维FFT计算为例，将行划分为个GPU任务分块，每个块中包含/2个线程，每个线程操作2个数据，基于该任务划分，个块可以并行执行。

2) 一维FFT计算。以点一维FFT为例，计算共分为(=log2)个串行层次，每个层次内部由/2个线程并行计算得到结果，每层计算完成后必须对/2个线程进行同步操作，才能保证下一层所需输入数据的正确性。

3 基于GPU的并行优化

在实际计算的时候，主要考虑从算法本身的优化、指令在GPU中执行的优化、数据存储的优化以及GPU中计算部署的优化等4个方面进行讨论。

3.1 算法优化

在GPU中进行并行计算，想要提升实时性，首先需要从算法本身入手。虽然现有用于GPU的算法也有一定的优化效果，但是还可以从以下2个方面进行进一步优化。

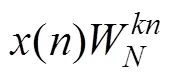
2) 矩阵转置优化。标准的二维FFT计算需要进行2次转置，对于在频域计算后还将变换回时域计算的情况，可不进行第2次转置直接后续计算，而转置计算的存储复杂度较高，每减少1次转置，内存访问次数降低2××。

从理论上分析，进行了这2种优化后，在计算速度上将会有所提高。

3.2 指令优化

指令执行是并行计算关键的一步，因此，指令运行导致的流水线问题以及一些复杂的指令运行都是优化的目标。

1) 解循环优化。在一维FFT计算时，通过循环对层计算进行流程控制，循环能够有效降低代码占用的存储空间，但是执行循环时，需要多次执行判断和跳转指令，破坏了GPU的执行流水线，降低了GPU的效率。对于实际工程，输入数据的长度是已知的，在计算前就能够计算出一共需要多少层计算，因此可以将整个循环展开，去除一维FFT计算中流程控制中的判断和跳转。

2) 复杂指令优化。

①取模计算优化：在一维FFT计算、矩阵转置中采用了大量取模计算进行下标计算[16]，取模计算需要进行多次除法计算，计算复杂。在实际工程中，输入数据的长度是已知的，而且通常是2的指数，这就可以用执行效率高的位运算代替取模计算。当=2时，(MOD)可以用&(−1)代替，可以实现1个时钟周期输出计算结果，无需常规取模计算所需的数百个时钟周期。

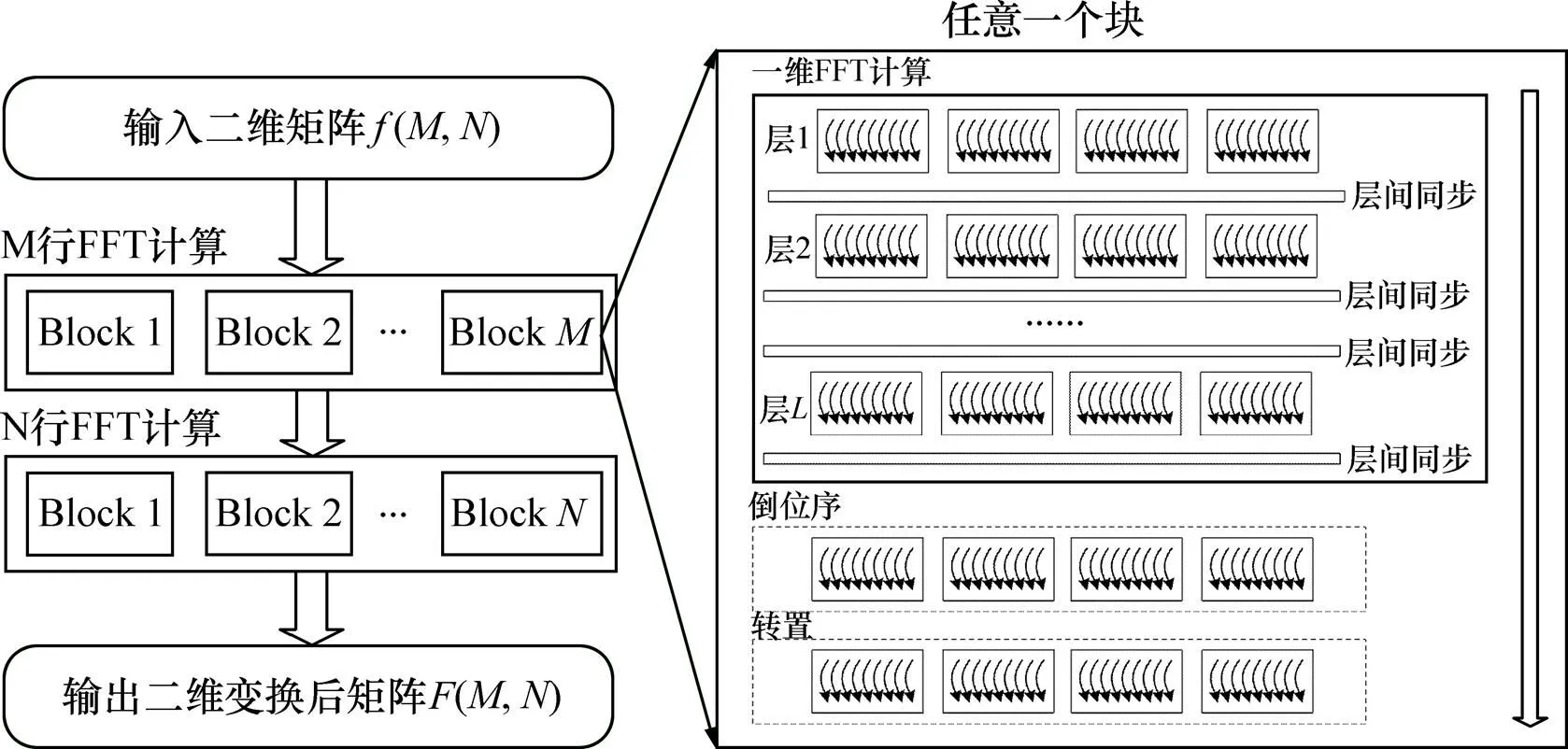
图2 二维FFT并行执行模型

②三角函数计算优化：在计算旋转因子W时，需要计算三角函数cos和sin，直接采用GPU提供的快速硬件指令取代函数实现，可以实现1个时钟周期输出计算结果，无需常规直接计算所需的数百个时钟周期，能够有效提高计算效率。

3.3 存储优化

1) 共享存储器优化。在GPU共享存储器的访问时，必须尽量避免访问冲突，当共享存储器的访问模式为32位时，访问一个复数需要2次操作，这导致了较多的共享存储器访问冲突；而采用64bit共享存储器访问方式，能减少冲突访问的次数，提高共享存储器的访问效率。

2) 用查表法取代复杂计算。倒位序操作涉及到多次循环和条件判断[16−17]，若每个点直接计算对应位序，则GPU难以达到较高的处理效率。在实际工程中，可根据实际计算的点数，事先计算好倒位序表，在倒位序计算时直接查表，对数据进行倒位序操作。

3.4 部署优化

GPU由于部署不同，在执行效率上会产生较大的差异。一般而言，必须使每个块中有尽可能多的线程，同时也要保证足够的分块数量，才能充分利用GPU的计算能力。在图2所示的并行模型中，每个块中的线程数量为数据长度的一半，每个线程仅操作2个数据，无法有效地屏蔽存储器访问延迟。因此，在保证分块数足够的前提下，应使每个线程操作更多的数据，如4个或8个数据。在实际工程中，可通过试差法，选择最优的部署。

4 实验结果及分析

高速小尺寸二维FFT优化方法的提出是为了提高图像复原算法的计算速度。因此，在实验中用乘性迭代算法(MIA)作为基础算法来对文中的小尺寸二维FFT算法进行精度及运算效率评测[2]。

实验测试平台如下：GPU 为NVIDIA公司的GeForce Titan Black(显存6GB)；CPU是i7 4770K，主频3.5G(4核)；内存16 G；测试程序在VC2010和CUDA6.5环境下编译完成。首先对算法的计算精度进行实验。

实验1的结果如图3所示。其中，图3(a)所示为原始图像，尺寸为128×128；图3(b)所示为人工卷积模糊后的图像；图3(c)所示为在CPU上采用Matlab执行MIA算法复原后的图像；图3(d)所示为GPU上执行MIA算法进行200次迭代复原后的图像。

实验2的结果如图4所示。其中，图4(a)所示为原始图像，尺寸为256×256；图4(b)所示为在CPU上采用Matlab执行MIA算法复原后的图像；图4(c)所示为GPU上执行MIA算法进行200次迭代复原后的图像。

从复原效果来看，Matlab复原图像基本与GPU复原图像一致，肉眼评价无法观测出二者之间的差异。表1所示为图3(c)与图3(d)、图3(b)与图3(c)的差异。从表1可知：GPU复原图像的精度非常好，其计算精度和Matlab结果相差不超过0.2%。

(a) 原始图像；(b) 降质图像；(c) Matlab复原图像；(d) GPU复原图像

(a) 原始图像；(b) Matlab复原图像；(c) GPU复原图像

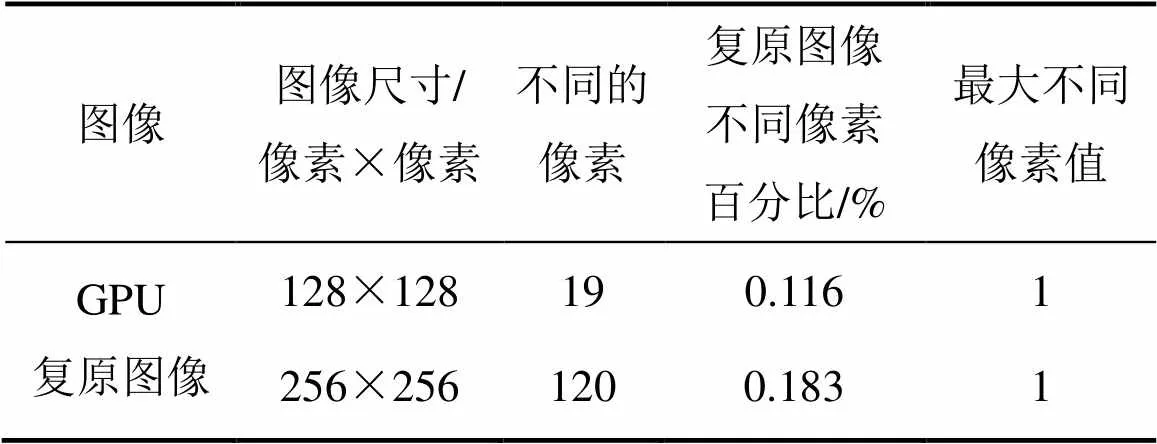
表1 GPU复原图像与Matlab复原图像比较

然后对复原算法的实时性进行实验。

为了与现有应用于GPU的复原CUFFT库图像复原算法进行对比，采用32×32，64×64，128×128和256×256这4种尺寸的图像进行模糊后，分别在相同的GPU平台上利用CUFFT库算法和MIA算法进行图像复原计算，其中迭代次数为200次，同时，在目前主流的CPU上对同样的算法处理速度进行对比实验。

表2所示为在GPU上使用CUFFT库算法和本文介绍方法对不同尺寸图像执行MIA算法的时间。算法需要执行1 200次二维FFT，执行时间为纯计算时间，没有包括从CPU到GPU的数据传输时间。CUFFT为采用标准CUFFT库函数的实验结果，CPU_S为采用标准C代码后的实验结果，GPU_F为采用本文优化策略后的实验结果。

从表2可知：当数据尺寸越小，采用本文优化策略相比标准CUFFT库函数取得的加速比越大；当数据规模为256×256时，本文优化策略仍能取得1.32倍的加速比，相比标准CPU至少可以取得1.81倍的加速比，与目前已知基于GPU的最快计算效率相比，仍然优越得多。在处理实际使用的128×128图像时，处理时间控制在19.6 ms以内，即50帧/s的处理速率，达到了实时图像复原处理速度的要求，并已在实际光电跟踪系统中得到了应用。

表2 耗时测试结果

5 结论

1) 根据跟踪识别系统对图像复原的实时性要求，介绍了在GPU上高效并行实现小尺寸二维FFT的方法，通过分析二维FFT的计算流程和算法特点，对二维FFT计算的可并行性进行了梳理；给出了二维FFT计算在GPU上的并行执行模型；提出了算法优化、指令优化、存储优化以及部署优化等基于GPU的并行优化策略，充分挖掘了GPU的性能。

2) MIA图像复原算法的运算实验效果表明本文的小尺寸二维FFT计算方法的精度基本与Matlab的一致，在多次迭代后仍能达到较高的精度。文中小尺寸二维FFT算法在处理不同尺寸的图像时，均达到了较优越的运算性能。

3) 在满足计算精度的基础上，计算速度满足实时图像复原处理速度的要求，相关优化策略已经在多项光电跟踪系统中得到应用，显示了本文方法的有效性和优越性。

[1] ZHANG Jianlin, ZHANG Qiheng, HE Guangming. Blind deconvolution of a noisy degraded image[J]. Applied Optic, 2009, 48(12): 2350−2355.

[2] ZHANG Jun, HU Shiqiang. A GPU-accelerated real-time single image de-hazing method using pixel-level optimal de-hazing criterion[J]. Journal of Real-Time Image Processing, 2014, 9(4): 661−672.

[3] ZHANG Jianlin, ZHANG Qiheng, HE Guangming. Multiframe blind image restoration based on a multiplicative iterative algorithm[J]. Optical Engineering, 2009, 48(2): 027004.

[4] 张全, 鲍华, 饶长辉, 等. 相位差算法在多GPU平台上的并行化实现[J]. 光电工程, 2016, 43(3): 66−72.ZHANG Quan, BAO Hua, RAO Changhui, et al. Parallel implementation of phase diversity algorithm on multi-GPU[J]. Opto-Electronic Engineering, 2016, 43(3): 66−72.

[5] XIE Lang, LUO Yihan, BAO Qiliang. GPU-based parallel algorithm for blind image restoration using midfrequency-based methods[C]//ISPDI 2013-Fifth International Symposium on Photoelectronic Detection and Imaging. Beijing, 2013: 89101R−89101R-10.

[6] MEYER-BAESE U, MEYER-BAESE A, GONZÁLEZ D, et al. Code obfuscation using very long identifiers for FFT motion estimation models in embedded processors[J]. Journal of Real-Time Image Processing, 2016, 11(4): 817−827.

[7] PUCHAŁA D, STOKFISZEWSKI K. Effectiveness of fast fourier transform implementations on GPU and CPU[J]. Przeglad Elektrotechniczny, 2016, 92(7): 69−71.

[8] 常方正, 赵银娣, 刘善磊. 遥感影像CVA变化检测的CUDA并行算法设计[J]. 遥感学报, 2016, 20(1): 114−128.CHANG Fangzheng, ZHAO Yindi, LIU Shanlei. CUDA parallel algorithm for CVA change detection of remote sensing imagery[J]. Journal of Remote Sensing, 2016, 20(1): 114−128.

[9] XU Ming, CHEN Feiguo, LIU Xinhua, et al. Discrete particle simulation of gas-solid two-phase flows with multi-scale CPU-GPU hybrid computation[J]. Chemical Engineering Journal, 2012, 207/208(10): 746−757.

[10] YANG Canqun, WU Qiang, HU Huili, et al. Fast weighting method for plasma PIC simulation on GPU-accelerated heterogeneous systems[J]. Journal of Central South University, 2013, 20(6): 1527−1535.

[11] CHU H, LI T, WANG P. IP address lookup by using GPU[J]. IEEE Transactions on Emerging Topics in Computing, 2016, 4(2): 187−198.

[12] 夏健明，魏德敏. 图形处理器在大规模力学问题计算中的应用进展[J]. 力学进展, 2010, 40(1): 57−63.XIA Jianming, WEI Deming. Advances in graphices processing units’ application to the computation of large-scale mechanical problems[J]. Advances In Mechanics, 2010, 40(1): 57−63.

[13] XIA Chao, GUAN Qingxiao, ZHAO Xianfeng, et al. Highly accurate real-time image steganalysis based on GPU[J]. Journal of Real-Time Image Processing, 2016, 11(Special Issue): 1−14.

[14] 李仕, 王晶, 孙辉. 基于图形处理器的实数FFT 在图像处理中的应用[J]. 光学精密工程, 2008, 16(12): 2414−2420. LI Shi, WANG Jing, SUN Hui. Real FFT based on graphic processing unit for image processing[J]. Optics and Precision Engineering, 2008, 16(12): 2414−2420.

[15] CAVICCHI T. DFT time-domain interpolation[J]. IEE Proceedings F: Radar & Signal Processing, 1992, 139(3): 207−211.

[16] COOLEY J, TUKEY J. An algorithm for the machine calculation of complex Fourier series[J]. Mathematics Computation, 1965, 19: 296−301.

[17] ZHANG Xinxue, WANG Guizeng. Parallel FFT architecture consisting of FFT chips[J]. Journal of Circuits and Systems, 2000, 5(2): 38−42.

(编辑 杨幼平)

Optimization on FFT of small size in real-time image restoration based on GPU

YAN Fabao1, SU Yarui1, ZHAO Zhanfeng2, ZUO Haorui3, LIU Jianxin4

(1. School of Mechanical, Electrical & Information Engineering, Shandong University, Weihai, Weihai 264209, China;2. Institute of Information Engineering, Harbin Institute of Technology, Weihai, Weihai 264209, China;3. Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu 610209, China;4. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China)

To meet the real-time demand of image restoration for recognition and tracking system, an optimization research on two-dimensional FFT of small size realized in graphics processor unit(GPU) efficiently was done. An analysis of two-dimensional FFT algorithm was analyzed first. And according to the characteristics of GPU, a parallel execution model based on graphics processor was proposed. Based on this model, the optimization research was done considering the aspects of algorithm complexity, the number of jump instructions, access conflict and access latency of the shared memory, and the utilization efficiency of GPU. And two-dimensional FFT computation of small size was realized in the GPU. In image restoration experiment, comparison on the calculation accuracy of two-dimensional FFT of small size optimization algorithm based on GPU and the traditional algorithm in MATLAB based on CPU was done. And a comparison on the computational efficiency of optimization algorithm proposed and the library function image restoration algorithm of CUFFT provided by NVIDIA Corp in four different sizes based on the same GPU platform was made. The results indicate that this optimization algorithm has excellent recovery performance, and human vision system could not distinguish the difference between the results and the MATLAB demonstrations. And the optimization algorithm can recover a frame of 128×128 gray fuzzy image within 19.6 ms, while the computing speed increases 1.8 times approximately compared with that using library function of CUFFT directly.

graphic processing unit (GPU); FFT of small size; image restoration; parallel optimization; real-time computation

10.11817/j.issn.1672−7207.2017.10.019

TP39

A

1672−7207(2017)10−2691−06

2016−10−13；

修回日期：2017−01−16

国家科技基础性工作专项(2013FY110800)；中国博士后科学基金资助项目(2016M600538)；国家自然科学基金资助项目(41674080，41574123，21505028)(Project(2013FY110800) supported by the National Science and Technology Basic Work; Project (2016M600538) funded by China Postdoctoral Science Foundation; Projects(41674080, 41574123, 21505028) supported by the National Science Foundation of China)

苏艳蕊，博士，讲师，从事跟踪控制平稳性研究、嵌入式系统研究，E-mail：suyanrui@126.com