卫星在轨微振动隔离系统动力学分析

刘大伟 陈卫东 刘兴天 周徐斌

(1南京航空航天大学,机械结构力学及控制国家重点实验室,南京 210016)(2上海卫星工程研究所,空间机热一体化技术实验室,上海 201109)

卫星在轨微振动隔离系统动力学分析

刘大伟1,2陈卫东1刘兴天2周徐斌2

(1南京航空航天大学,机械结构力学及控制国家重点实验室,南京 210016)(2上海卫星工程研究所,空间机热一体化技术实验室,上海 201109)

针对采用主动隔振系统时,有效载荷和卫星平台因质量接近而产生的运动耦合问题,文章使用牛顿-欧拉(Newton-Euler)方法对设计的Stewart隔振系统进行动力学建模,给出了有效载荷和卫星平台质量接近时运动耦合模型,以及卫星平台质量无穷大时的运动无耦合模型下的系统动力学方程,对比分析了两种模型下系统动力学响应。结果表明:Stewart隔振系统在两种模型下系统动力学特性差异较大,有效载荷和卫星平台质量接近时,运动耦合模型的有效载荷角振动响应峰值大、平动响应峰值小、系统模态频率较高。因此,有效载荷和卫星平台质量接近时应采用运动耦合模型进行动力学建模。研究结果可为卫星有效载荷微振动隔离提供理论参考。

Stewart隔振系统;微振动;运动耦合;动力学分析

1 引言

卫星在轨运行时星上的转动部件(如飞轮)引起的幅值小、频带宽振动称为微振动。微振动显著地影响了星上精密有效载荷的正常工作,使其成像模糊甚至失败[1]。为了抑制星上微振动,可采用被动控制、主动控制等多种减振方案[2]。微振动被动减振方案中,文献[3]采用折叠悬臂梁减振方案,该结构在100～300 Hz有显著减振效果;文献[4]采用非线性阻尼隔振系统可抑制隔振系统共振峰值。被动减振方案的缺点是隔振频带有限,考虑到星上微振动频带宽的特点,需要主动控制方法来实现宽频隔振。使用主动控制方法进行隔振时,为有效获取空间六自由度隔振,通常将作动器布置成基于Stewart平台的隔振系统构型。美国的喷气推进实验室(JPL)最早采用音圈电机实现了立方体构型的Stewart隔振系统,并进行了微振动试验研究[5];文献[6]提出了一种“有加速度反馈的主动力反馈+天棚阻尼(PFF+Skyhook)控制”方法,该方法在不影响控制效果情况下使振动衰减频率起始点降低到1.93 Hz;文献[7]使用自适应滤波主动控制算法对基础干扰进行了主动控制,单频干扰可实现30 dB抑制效果。文献[8-9]也对Stewart隔振系统进行了理论和试验研究。他们在进行Stewart隔振系统理论分析时,采用的都是基于地面试验模型,卫星平台的质量简化为无穷大,没有考虑有效载荷和卫星平台之间的运动耦合。当卫星在轨运行时,处于微重力无约束状态,有效载荷与卫星平台运动相互耦合,尤其当有效载荷与卫星平台质量较为接近时,不能忽略二者运动耦合对Stewart隔振系统动力学特性的影响,将卫星平台等效为质量无穷大的模型已不再适用,需要对空间无约束状态下考虑运动耦合的Stewart隔振系统进行动力学建模与分析。

本文以基于Stewart平台的卫星隔振系统动力学建模为背景,考虑在轨运行时Stewart隔振系统中有效载荷与卫星平台运动相互耦合,在笛卡尔坐标系下使用Newton-Euler方法建立了空间无约束状态考虑有效载荷与卫星平台运动耦合的Stewart隔振系统动力学模型,并将该理论模型计算得出的模态同有限元结果相比较,验证了模型的正确性;同时给出了卫星平台质量无穷大时不考虑运动耦合的隔振系统动力学模型,对比分析两种模型下隔振系统动力学特性,说明了建立考虑运动耦合的隔振系统动力学模型的必要性,为以后微振动主动控制研究提供理论参考。

2 Stewart隔振系统动力学建模

2.1 Stewart隔振系统参数

Stewart隔振系统是实现六自由度隔振所需作动器个数最少的构型,由上下两个连接平台和六个可自由伸缩的支腿组成。根据某卫星包络条件设计了立方体构型的Stewart隔振系统,相邻支腿间相互正交,其构造如图1所示。

隔振系统采用圆柱圆弧切口柔性铰消除了传统球铰和万向铰存在回退空程的问题[10],其力学特性接近球铰。支腿由压电作动器和力传感器串联组成,力传感器用于主动控制中力信号反馈。考虑到压电作动器内部结构复杂,将压电作动器结构简化成两根相同长度和质量的杆通过滑动副连接的模型。支腿上部由压电作动器简化模型中的上杆组成,质心位置为其质心距上铰接点距离;支腿下部由压电作动器简化模型中的下杆和力传感器组成,质心位置为其质心距下铰接点距离。每个支腿的控制力作用于滑动约束处,为fi=-c˙Li+k(λVVi-ΔLi),i为支腿数,i=1,2,…,6。其中,c为压电作动器的阻尼系数,k为压电作动器的刚度,λV为压电作动器位移作动因子,Vi为驱动电压,Li为支腿长度,ΔLi为支腿长度变化量。该隔振系统相关参数见表1,卫星平台和有效载荷的质量比约为5。

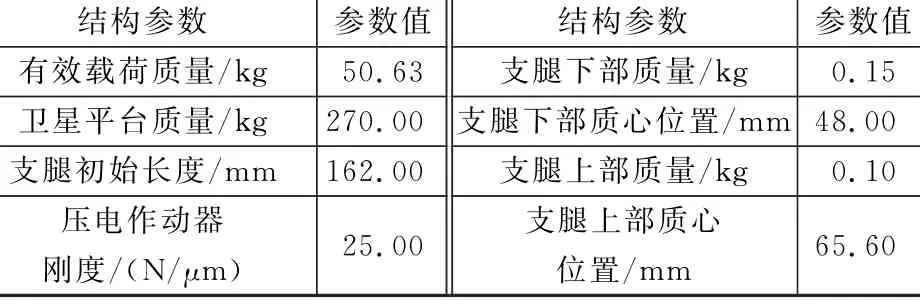
表1 立方体构型Stewart隔振系统相关参数Table 1 Parameters of the Stewart platform with cubic configuration

2.2 支腿力学分析

为了建立运动耦合模型的隔振系统动力学方程,首先对支腿进行力学分析得到铰接力,然后使用铰接力分别获得有效载荷与卫星平台动力学方程,将前述方程整合获得隔振系统整体动力学方程。根据2.1节中关于压电作动器的简化模型,可以获得支腿的简化模型,如图2所示。有效载荷连体坐标系为{P},卫星平台连体坐标系为{B},空间惯性坐标系为{O}。Pi、Bi分别为第i根支腿与有效载荷、卫星平台铰接点;rOPi、rOBi为铰接点Pi、Bi在{O}中的坐标向量;rOP、rOB分别为{P}、{B}坐标原点在{O}中的坐标向量;φi为第i根支腿轴向转动角度。si表示由Bi指向Pi的单位向量,~si表示向量si的反对称矩阵。

有效载荷质心PC在{P}中的坐标向量为rPP,C卫星平台质心BC在{B}中的坐标向量为rBBC。TOP、TOB为{P}坐标系、{B}坐标系到{O}坐标系的转换矩阵,ωP,˙ωP为连体坐标系{P}的转动角速度、角加速度,ωB,˙ωB为连体坐标系{B}的转动角速度、角加速度。第i根支腿控制力为fi,则滑动约束处约束力为Fi=si·Fi·si+fi·si。若铰接处力矩为MOPi、M OBi,忽略高阶小量,可得铰接处作用力为

式中:QPPi,QPBi,QBPi,QBBi,Qφi为隔振系统结构参数组成的张量矩阵,同时可以得到支腿绕轴向的转动平衡方程为

式中:Mφi=为支腿结构参数组成的张量矩阵,为支腿上、下两部分惯性张量的矩阵和。

2.3 隔振系统动力学建模

卫星在轨运行时处于空间无约束状态,此时有效载荷的运动对卫星平台空间位姿也会产生影响,即卫星平台运动和有效载荷运动存在耦合,如果有效载荷质量和卫星平台质量接近,则不能忽略该耦合对系统动力学特性的影响。为了分析运动耦合对Stewart隔振系统动力学特性的影响,需要分别建立运动耦合模型与运动无耦合模型的动力学方程,其结构示意分别如图3(a)、(b)所示。

首先建立图3(a)运动耦合模型的动力学方程,在无外力作用下,整合有效载荷平衡方程和转动平衡方程,可以得到

式中:MBP、MBB、MBφ为卫星平台质量相关的常值矩阵;QBf为作动力到卫星平台质心处的力雅克比矩阵,QBCK为卫星平台相关结构参数组成的矩阵。对于支腿绕轴向转动平衡方程,将六根支腿的方程组合可以得到

式 中:MφP、MφB、Mφφ为 常 值 质 量 矩 阵;QφCK=sT1(MOP1+MOB1)…sT6(MOP6+MOB6

[])T。整合式(4)～(6)得到运动耦合模型下系统的18自由度动力学方程为

当卫星平台与有效载荷质量比足够大时,有效载荷运动对卫星平台位姿影响极小,此时可忽略运动耦合对系统动力学特性的影响(地面试验中卫星平台通常会受到约束,此时卫星平台质量认为无穷大,也属于该种模型),系统模型如图3(b)所示。忽略运动耦合时,只需要考虑有效载荷动力学方程和支腿绕轴向转动平衡方程。将卫星平台运动看做系统的基础激励,即可得到无耦合模型下隔振系统的动力学方程[8]。

3 Stewart隔振系统动力学特性

3.1 本文理论模型模态与有限元模型模态对比

为了验证上述数学模型的正确性,根据2.1节中给出的相关参数,使用MSC/Patran软件计算该Stewart隔振系统的有限元振动模态。忽略刚体模态,给出前6阶模态振型和频率如图4所示,模态振型图中不同颜色代表不同的变形量,颜色越偏向红色代表变形量越大,越偏向蓝色代表变形量越小。

另外,给出根据上述本文理论模型得出的前6阶模态中有效载荷的振型矩阵如下:

其中,每一列代表一个模态,按照模态频率升序排列,对应的模态频率见表2。将上述振型矩阵与图4中有限元计算结果相比较,可发现对应模态的振型一致。考虑到本文理论模型中支腿只考虑了轴向刚度,其他元件作为刚体处理,而有限元中所有元件都当作柔性体,因此有限元中的系统整体刚度小于本文理论模型,有限元计算得出模态频率应略小于本文理论计算结果。比较表2中本文理论和有限元对应模态频率,本文理论模型的六阶模态频率略大于MSC/Patran软件计算得出的结果,但是误差都在8%以内,说明了本文理论模型的正确性。

表2 有限元计算与本文理论推导的前六阶模态频率Table 2 First 6 mode frequencies of FEM and theory in this paper

3.2 隔振系统动力学响应

根据表1中给出的结构参数,分别采用2.3节中耦合和无耦合模型的系统动力学方程,在耦合模型中取卫星质量与有效载荷质量之比为5,得出从卫星平台质心处到有效载荷质心处位移响应传递率曲线,如图5所示。

由图5可知,两种模型下x、y方向平动和绕x轴、y轴转动传递率曲线并不重合,峰值处曲线分离;z方向平动和绕z轴转动传递率曲线基本重合。对比位移传递率曲线可以发现:①平动自由度中,两种模型下曲线在10～52 Hz中低频段分离;转动自由度中,两种模型下曲线在高于30 Hz分离;②运动耦合模型下x、y平动峰值处幅值分别降低了约7.6 dB和7.3 dB,而绕x、y轴转动的峰值处则增长了约5.5 dB和5.7 dB;③耦合模型峰值频率高于无耦合模型频率。综上,当卫星平台和有效载荷质量接近时,如本文取质量比为5时,无耦合模型下系统动力学响应与耦合模型在全频段都有较大差异。因此,卫星平台和有效载荷质量接近时,运动耦合对系统动力学特性有很大影响,此时应使用耦合模型下动力学方程。

4 结论

本文建立了卫星在轨运行时考虑有效载荷与卫星平台运动耦合的Stewart隔振系统动力学方程;并给出运动无耦合模型下系统动力学方程。得到如下结论:

(1)使用Newton-Euler方法建立的空间无约束状态下Stewart隔振系统动力学模型,能够精确描述运动耦合模型下系统动力学特性,根据本文理论模型分析得出的系统模态与有限元分析结果一致。

(2)当卫星平台与有效载荷质量比较小,如文中取质量比为5时,有效载荷与卫星平台运动耦合对系统动力学特性有显著影响,有效载荷和卫星平台质量接近时,运动耦合模型的有效载荷角振动响应峰值大、平动响应峰值小、系统模态频率较高。

(3)使用Stewart隔振系统时,应明确卫星平台与有效载荷的质量比,分析运动耦合对系统动力学特性的影响,然后据此选用合适的动力学模型。

References)

[1]董瑶海.航天器微振动[M].北京:中国宇航出版社,2015 Dong Yaohai.Spacecraft micro-vibration[M].Beijing:China Astronautics Press,2015(in Chinese)

[2]Liu C,Jing X,Daley S,et al.Recent advances in micro-vibration isolation[J].Mechanical Systems&Signal Processing,2015,56/57(1):55-80

[3]Zhou W,Li D.Experimental research on a vibration isolation platform for momentum wheel assembly[J].Journal of Sound&Vibration,2013,332(5):1157-1171

[4]H Laalej,Z Q Lang,S Daley,et al.Application of nonlinear damping to vibration isolation:an experimental study[J].Nonlinear Dynamics,2012,69:409-421

[5]Rahman Z,Spanos J,Laskin R,et al.A six axis vibration isolation,suppression and steering system for space applications[C]//Aerospace Sciences Meeting and Exhibit.Washington D.C.:AIAA,1997:910

[6]李伟鹏,黄海,黄舟.基于Stewart平台的星上微振动主动隔离/抑制[J].机械科学与技术,2015,34(4):629-635 Li Weipeng,Huang Hai,Huang Zhou.Active isolation/suppression for satellite micro-vibration with Stewart platform[J].Mechanical Science and Technology for Aerospace Engineering,2015,34(4):629-635(in Chinese)

[7]王超新,刘兴天,张志谊.基于立方体Stewart的微振动主动控制分析与实验[J].振动与冲击,2017,36(5):208-213 Wang Chaoxin,Liu Xingtian,Zhang Zhiyi.Micro-vibration active control for a Stewart platform with a cubic configuration[J].Journal of Vibration and Shock,2017,36(5):208-213(in Chinese)

[8]Wang Z,Zhang W.Adaptive active vibration control for a piezoelectric stewart platform[C]//IEEE International Conference on Intelligent Computing and Intelligent Systems.New York:IEEE,2009:752-756

[9]Hanieh A A,Preumont A.Multi-axis vibration isolation using different active techniques of frequency reduction[J].Journal of Vibration&Control,2011,17(5):759-768

[10]赵晓颖,温立书,么彩莲.欧拉角参数表示下姿态的二阶运动奇异性[J].科学技术与工程,2012,12(3):634-637 Zhao Xiaoying,Wen Lishu,Me Cailian.The Secondorder kinematic singularity of orientation in euler parameters represention[J].Science Technology and Engineering,2012,12(3):634-637(in Chinese)

Dynamic Analysis of In-orbit Satellite Micro-vibration Isolation System

LIU Dawei1,2CHEN Weidong1LIU Xingtian2ZHOU Xubin2
(1 State Key Laboratory of Mechanics and Control of Mechanical Structures,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)(2 Laboratory of Space Mechanical and Thermal Integrative Technology,Shanghai Institute of Satellite Engineering,Shanghai 201109,China)

Motions of payload and satellite are coupled in an active Stewart vibration isolation system if they have similar mass.The Newton-Euler method is used to establish dynamic equation of the Stewart vibration isolation system in this paper.Dynamic equation of the motion coupling model in which payload and satellite have similar mass and dynamic equation of motion uncoupling model in which satellite has infinite mass are established.Dynamic responses of the two models are analyzed and compared.The result shows that dynamic characteristics of the Stewart vibration isolation system using above models are quite different.If the mass of payload is similar satellite,the motion coupling model has large peak value of rotation,small peak value of translational and high system mode frequency.Therefore,it is essential to use the motion coupling model if payload and satellite have similar mass.This study provides guidance for satellite micro-vibration isolation.

Stewart vibration isolation system;micro-vibration;motion coupling;dynamic analysis

V414

A

10.3969/j.issn.1673-8748.2017.05.006

2017-08-21;

2017-09-12

国家自然科学基金(51505294)

刘大伟,男,硕士研究生,研究方向为复杂结构动力学与控制。Email:liudawei92@163.com。

(编辑:李多)